Homophily-Based Social Group Formation

in a Spin Glass Self-Assembly Framework

in collaboration with

Simon Lindner

Tuan Pham

Rudolf Hanel

Stefan Thurner

Journal Ref.: Phys. Rev. Lett. 130 (2023) 057401 

Slides available at: https://slides.com/jankorbel

More about me: https://jankorbel.eu

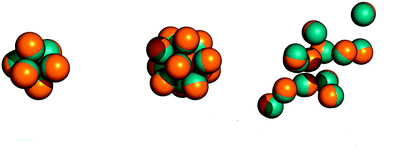
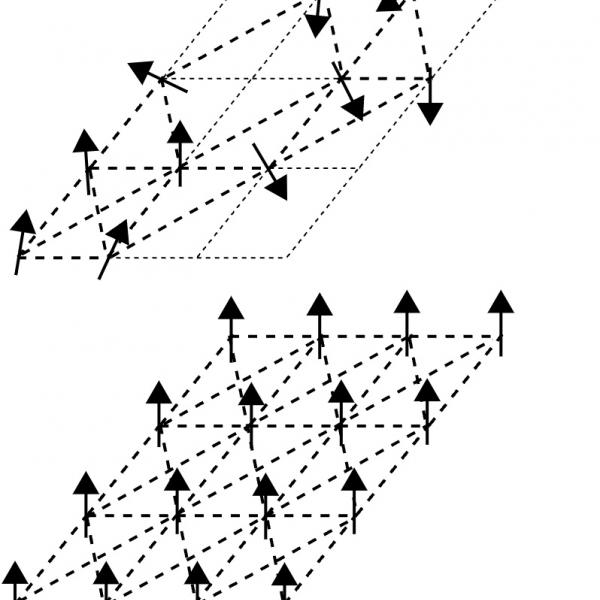
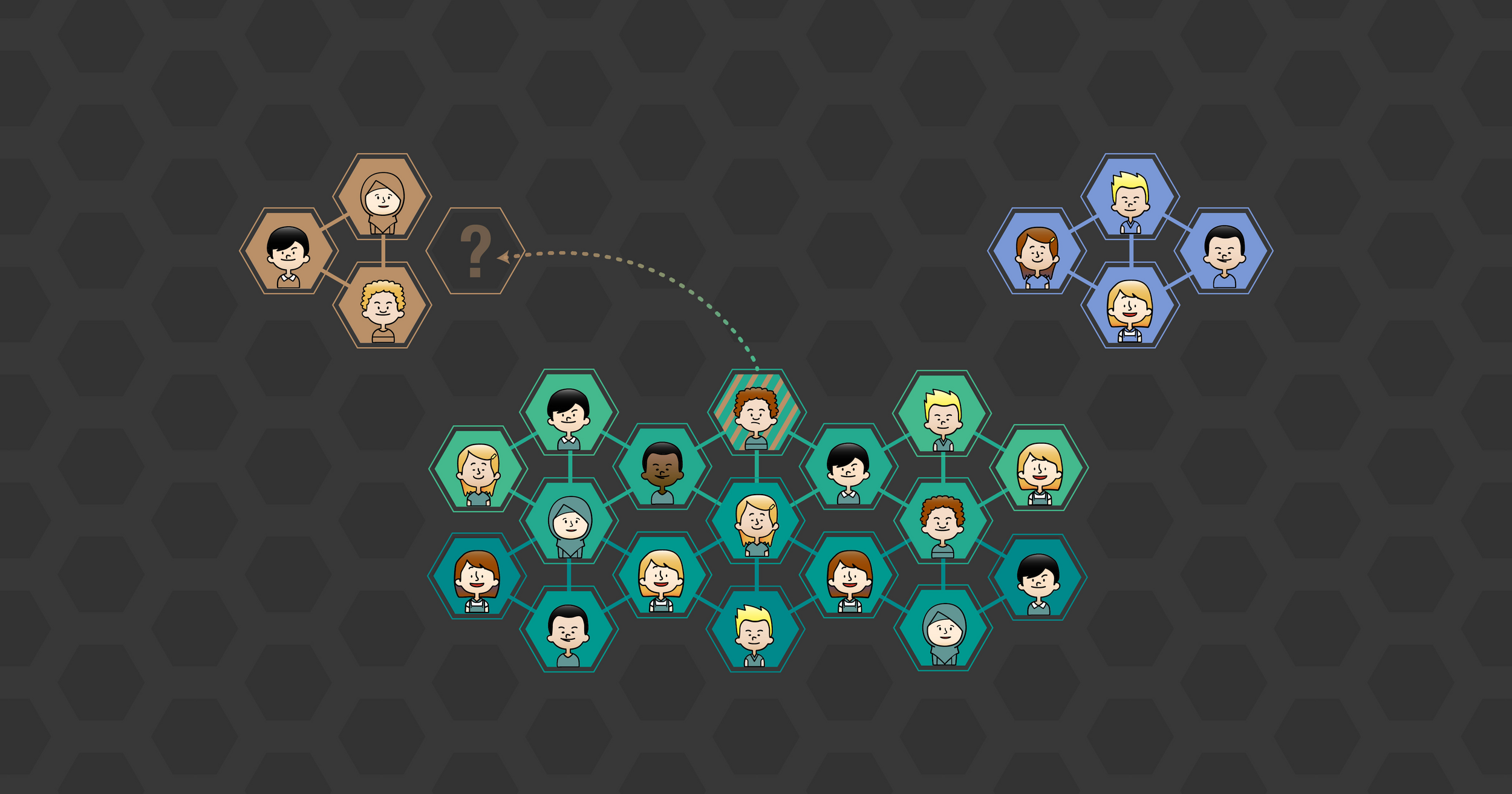
Graphical abstract

soft-matter self-assembly

 condensed matter spin glasses

social group formation

Homophily-Based Social Group Formation

in a Spin Glass Self-Assembly Framework

Paper flow

1.

2.

3.

1. Thermodynamics of

structure-forming systems

Entropy for systems with structures

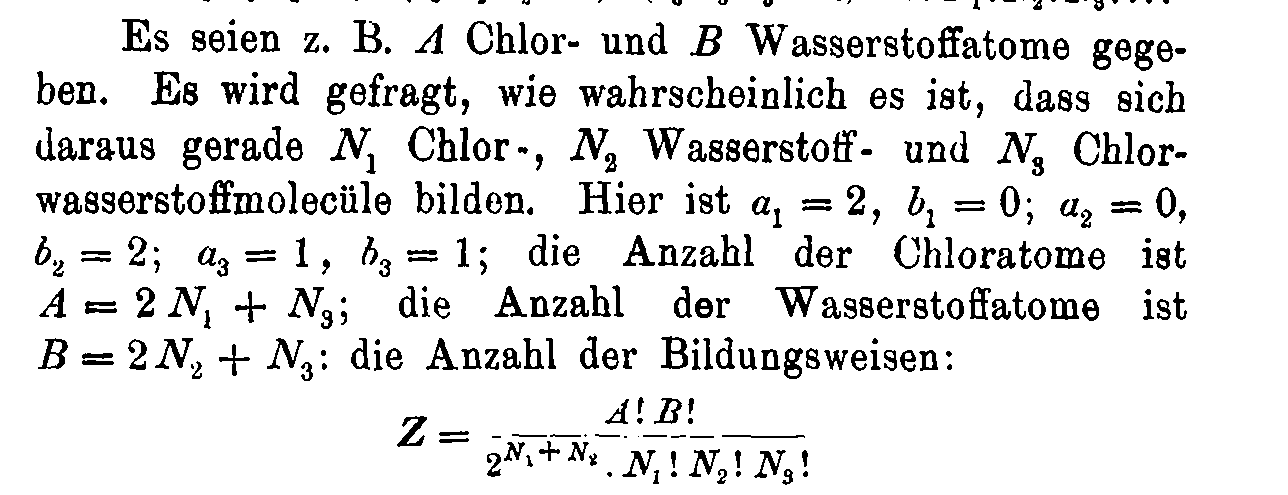
\(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}!   \textcolor{red}{(j!)^{n_i^{(j)}}}}\)  

$$\mathcal{S} = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log  \frac{j!}{n^{j-1}}}$$

\( S = k \cdot \log W\)

\( \wp_i^{(j)} = n_i^{(j)}/n\)

When we want to calculate the MaxEnt distribution, we maximize the entropy w.r.t. to 

• normalization \(\sum_{ij} j \wp_{i}^{(j)}=1\)
• average energy \(\sum_{ij} \wp_{i}^{(j)} \epsilon_{i}^{(j)} = E\)

Equilibrium distribution:

$$\hat{\wp}_i^{(j)} = \frac{n^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$

Normalization:

\(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{n^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{red} \alpha}\)

Free energy:

\( F = U - \beta^{-1} S = - \frac{\alpha}{\beta} {\color{red}- \frac{\mathcal{M}}{\beta}}\)

where \(\mathcal{M} = \sum_{ij} \wp_{i}^{(j)}\) is the number of molecules

MaxEnt distribution and free energy

Applications to self-assembly

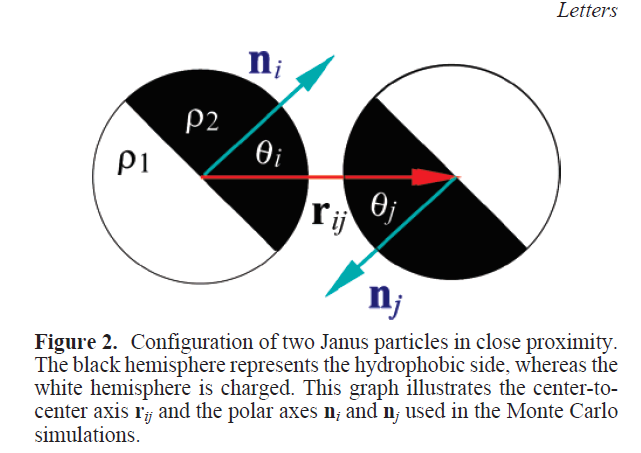
2. Spin-glass based opinion dynamics

• Many opinion dynamics systems follow two basic concepts:

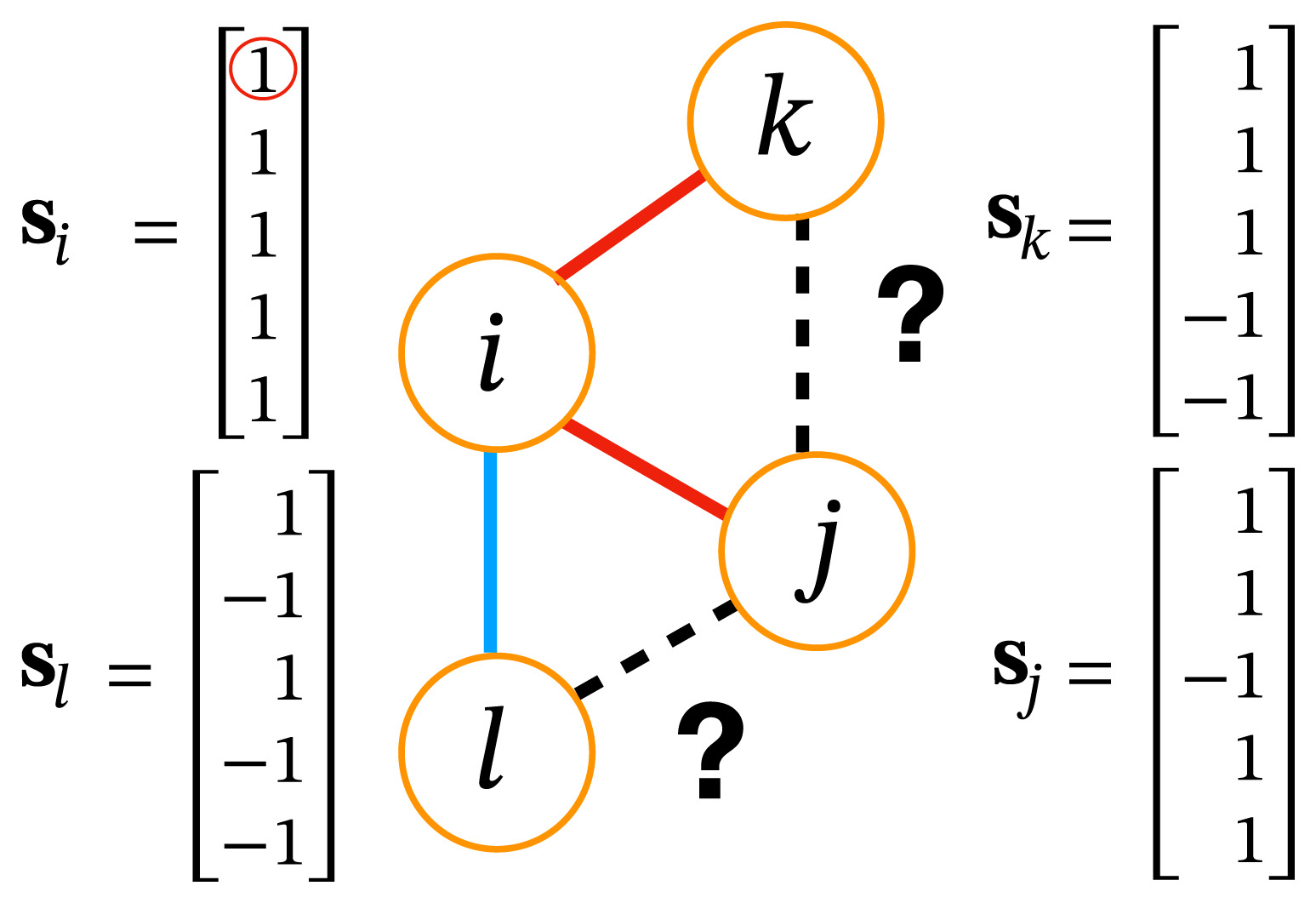
1. ​Homophily - people tend to be friends with peers with similar opinions ("birds of a feather flock together")

2.Social balance - people tend to follow Heider balance relation

("a friend of my friend is my friend, enemy of my friend is my enemy")

2. Spin-glass based opinion dynamics

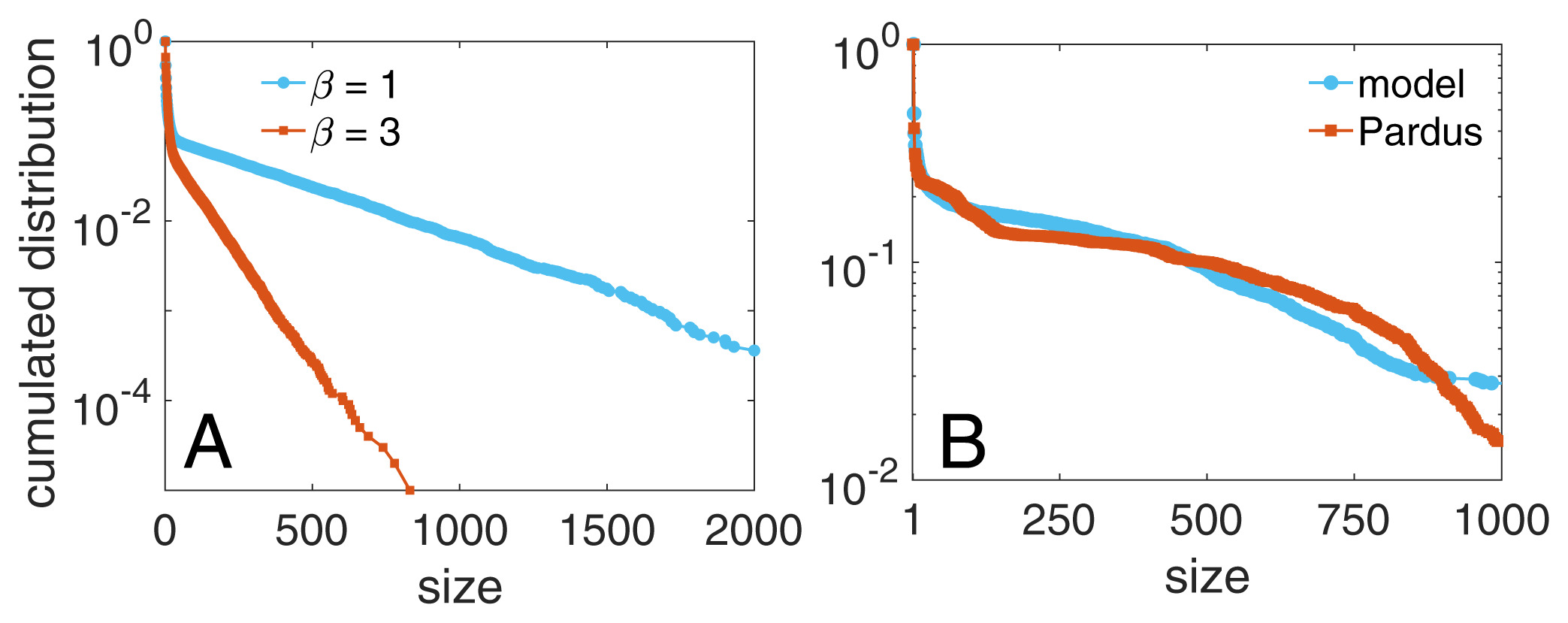
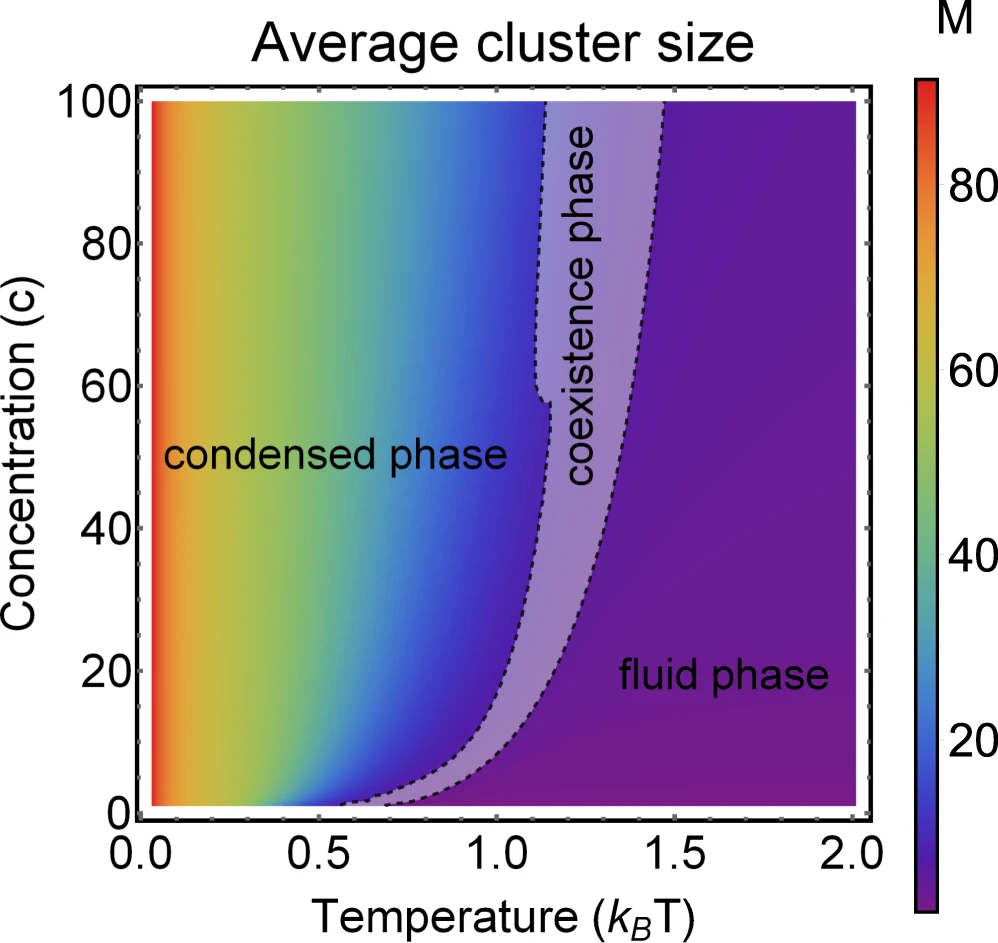
Group size distribution

Paper result: Social balance can emerge from homophily

3. Social group formation in the spin-glass self-assembly framework

Hamiltonian of a group \(\mathcal{G}\)

\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) =  \textcolor{red}{\underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{intra-group \ social \ stress}} \textcolor{blue}{ + \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{inter-group \ social \ stress}} \\ \qquad \qquad \qquad \qquad - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)

Group formation based on opinion= self-assembly of spin glass

Group 1

Group 2

friends

enemies

Approximations used in the model

1. Configuration model 

- We do not know the full network, just a degree distribution.        \(\Rightarrow\) The probability of observing a link between \(i\) and \(j\) is proportional to the degree of both nodes

2. Mean-field approximation

- We use the mean-field approximation of the Hamiltonian.

These two approximations lead to the set of self-consistency equations:

$$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$

where \(q^{(k)}\) is the intra-group degree, \(q^{(k,l)}\) is the inter-group degree and \(P\) is the degree distribution

Results for zero inter-group degree

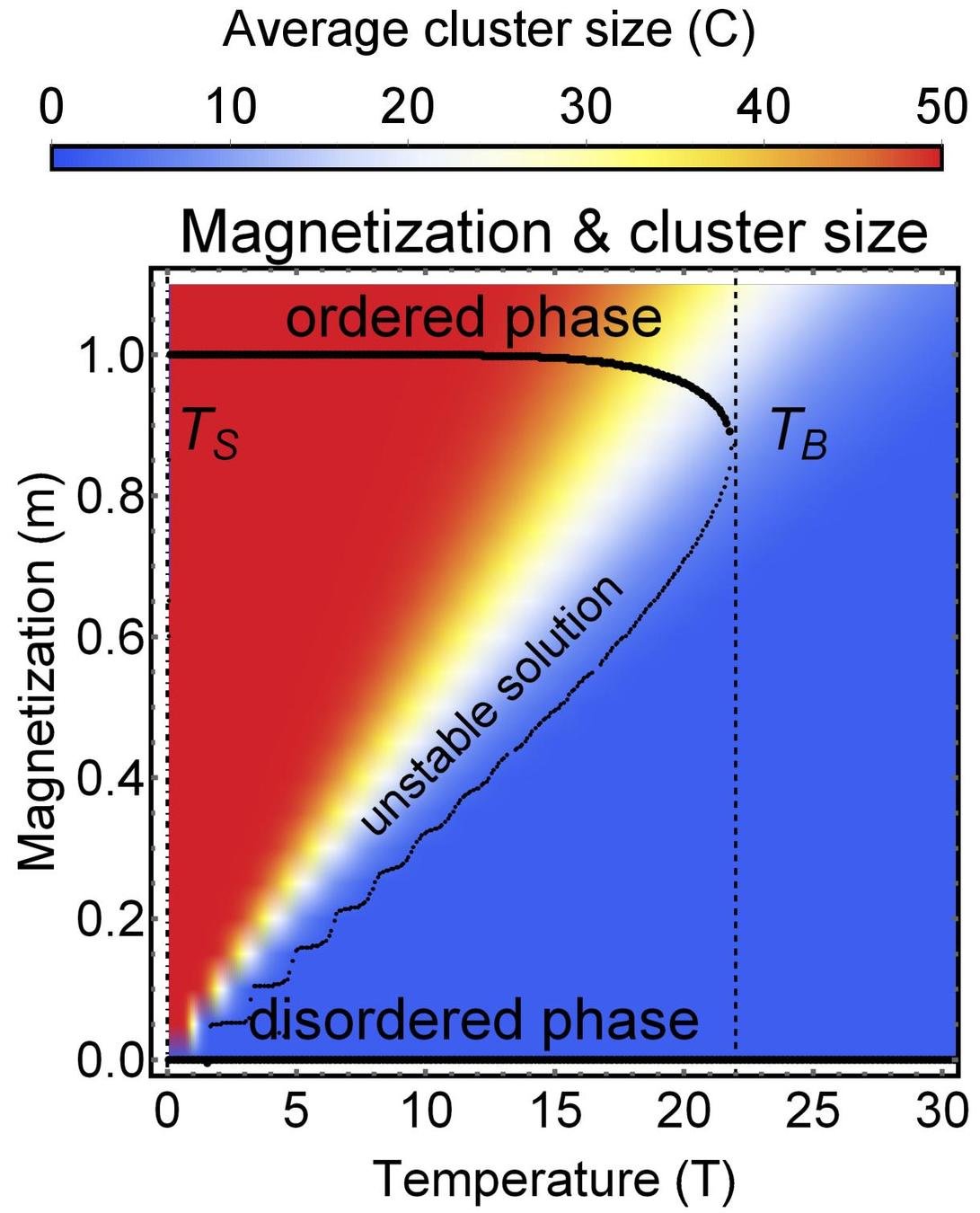
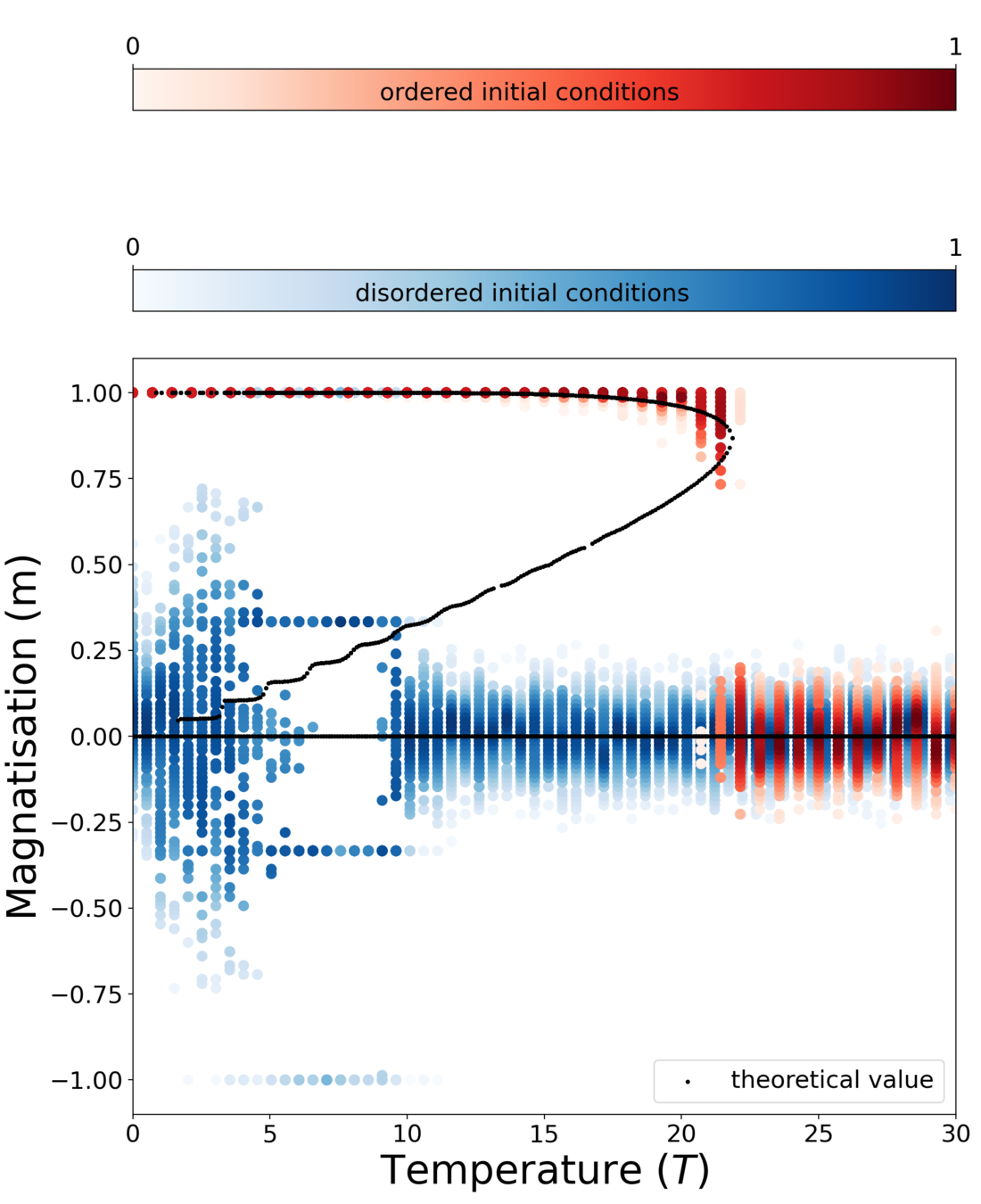
Theory

MC simulation

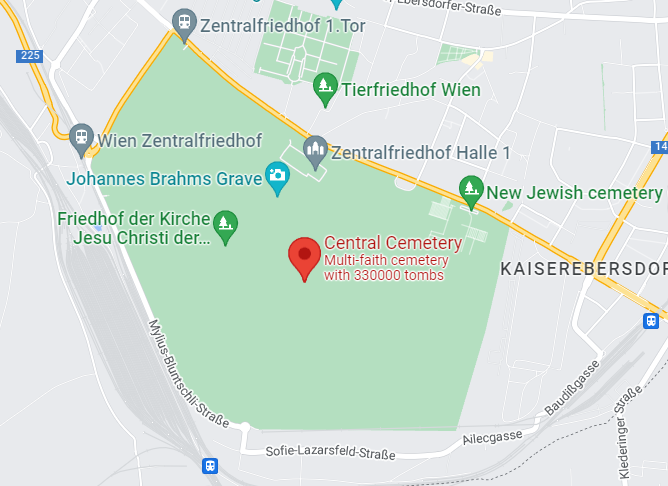
Application online multiplayer game PARDUS

+

=

Science is interdisciplinary.

Thank you