From Spins to Society:

Modeling Collective Social Behavior

with Statistical Physics

Jan Korbel

Slides available at: slides.com/jankorbel

Personal web: jankorbel.eu

Motivation

• Modeling the social systems is typically a very complicated and complex task

• Many different approaches are used to model social systems - agent-based models, for example

• One way of modeling the social systems is to use the methods of statistical physics to describe the social behavior

• The application of statistical physics methods in social systems gave rise to a new field - sociophysics

•  Most of the sociophysics models are based on simplifying assumptions.
  • These assumptions allow us to use the methods of statistical physics and (at least qualitatively) study the macroscopic behavior of social systems.
•  The main aim of sociophysics, therefore, is different from the application of statistical physics in natural systems
  • In natural systems, we ideally want to fully understand the phenomena that can be observed in the system
  • This is typically possible since natural systems have many symmetries
  • Social systems, on the other hand, are more complex, and therefore, complete understanding is almost impossible

Initial Remark

Some pioneering models

• Voter model - agents influence each other to change their opinions

​​

• Sznajd model -  model is based on a concept of social validation

• Axelrod model - describes the cultural dissemination

• Bounded confidence models- Individuals adjust their opinions if they are sufficiently close

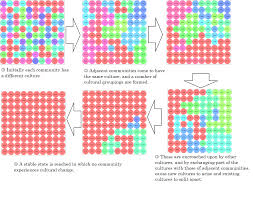
Main driving mechanisms

Homophily

• Dyadic relation between opinions of pairs
• "Birds of a feather flock together"
• People tend to like other peers with similar opinions

• McPherson, Smith-Lovin and Cook (2001). Annual Review of Sociology. 27: 415–444.

Social balance

• Triadic relation between friendly and inimical relations  
• "friend of my friend is my friend, enemy of my enemy is my friend"
• People tend to prefer balanced triangle relationships
• Heider (1946). The Journal of Psychology. 21: 107–112.

Main driving mechanisms

Physical interpretation

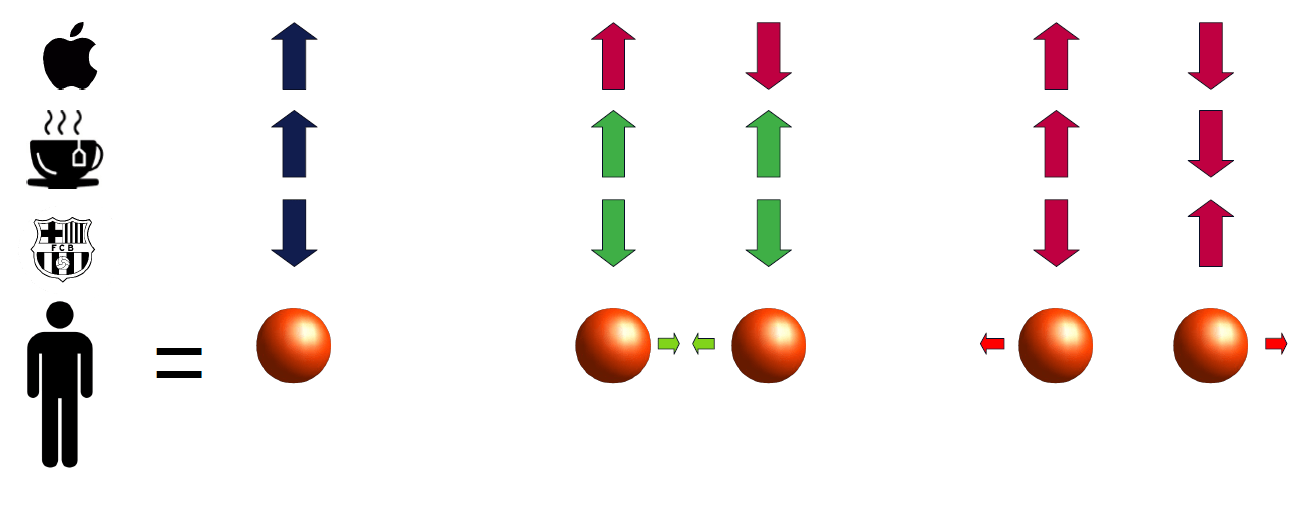
• We now discuss how these mechanisms can be translated into statistical physics models
• We model the individuals as particles and their opinions as (binary) spins
• The social models then correspond to various Ising-type models

Social Hamiltonian

• In statistical physics, the main quantity is the Hamiltonian, which quantifies the energy of the system 
• The system tends to reach the minimal energy state
• Here, the social Hamiltonian plays the role of social stress
• Similarly to physics, individuals tend to minimize their social stress as much as possible
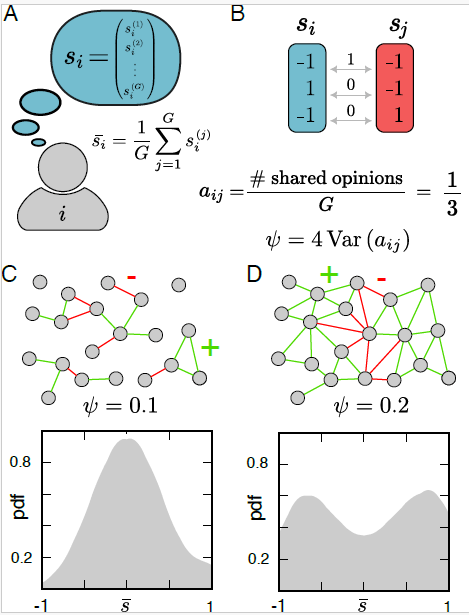
• We define the opinion vector of individual \(i\) as $$s_i= \{s_i^1,\dots,s_i^G\} \in \{-1,+1\}^G$$
• We also define the relations between individuals as $$A_{ij} \in \{-1,0,1\}$$ for inimical, non-existent, and friendly relations, respectively
• In some situations we only consider friendly or none relations

Social Hamiltonian for homophily

• Let us first consider that \(A_{ij} \in \{0,1\}\)
• For homophily, the Hamiltonian can be written as $$H(s_i) = - J \sum_{ij} A_{ij} s_i \cdot s_j$$ where \(s_i \cdot s_j := \frac{1}{G} \sum_{k=1}^G s_i^k s_j^k\) measures the similarity between opinion vectors \(s_i\) and \(s_j\)
• This corresponds to the Ising model with multiple layers of spins, each corresponding to one opinion type

Social Hamiltonian for social balance

• In this case, the social balance is solely about relations
• Therefore, it is independent of the opinions 
• Assuming the adjacency matrix \(A_{ij} \in \{-1,0,1\}\)
• The social balance Hamiltonian can be defined as $$H(A_{ij}) = - J\sum_{ijk} A_{ij} A_{jk} A_{ki}$$
• The cubic term \(A_{ij} A_{jk} A_{ik}\) is equal to:
  • +1, if the triangle is balanced
  • - 1, if the triangle is unbalanced
  •   0, if the triangle is not closed
• This corresponds to the Baxter-Wu model on the links

Combining homophily and social balance

• Both phenomena have been extensively studied separately
• By combining both terms, we obtain the Hamiltonian describing both homophily and social balance $$H(s_i,A_{ij})= -  \sum_{ij} A_{ij} s_i \cdot s_j - g \sum_{ijk} A_{ij}A_{jk}A_{ki}$$
• In this model, both opinions and relations co-evolve together
• It was first introduced in

[1] J. R. Soc. Interface. (2020) 1720200752

Social fragmentation 

• The system exhibits a phase transition between balanced and unbalanced state
• We define \(f = \frac{n_{+}-n_{-}}{n_{+}+n_{-}}\) where \(n_\pm\) is the number of (un)balanced triangles
• We observe the transition from a fragmented to a polarized society which depends on the network degree \(k\)

• The main issue with this model is that it does not relax to the global minimum but often gets stuck in a local minimum
• This is known as a rough energy landscape
• Furthermore, it is unrealistic that individuals would update their opinions and have in mind whether these changes result in a shift in balanced triangles into unbalanced
• Therefore, a more realistic approach is to assume that individuals can update their opinions by not anticipating the change in the triadic balance for all possible triangles

Rough energy landscape

Local Hamiltonian approach

[2]  Sci. Rep. (2021) 11, 17188

• We generalize the Hamiltonian model to consider an agent-based model, where the agents try to optimize their individual social stress
• A social stress of an individual \(i\) can be written as $$H^i(s_{i}) = - \sum_{j \in \mathcal{N}_i} A_{ij} s_i s_j - \sum_{j,k \in \mathcal{Q}_i} A_{ij} A_{jk} A_{ki}$$
• Here, the relation between two individuals is determined as \(A_{ij} = \mathrm{sign}(s_i \cdot s_j)\), so friendly we the two individuals have more common than different opinions and vice versa
• \(\mathcal{N}_i\) is the neighborhood of \(i\)
•  \(\mathcal{Q}_i\) is a fraction of triangles that contain \(i\)

Monte Carlo update with limited rationality

• The evolution is given by the following algorithm:
  1. Initialize opinion vectors
  2. Update
     • Pick a node at random
     • Pick a fraction of triangles \(q_i=\mathcal{Q}_i/N ^\Delta_i\) at random
     • Try to flip one opinion at random
     • Accept the flip with probability \( \min\{1,e^{-\beta \Delta H^i}\}\)
  3. Repeat until the system converges
• By taking into account a fraction of triangles, the agents can be irrational and increase the total social stress 

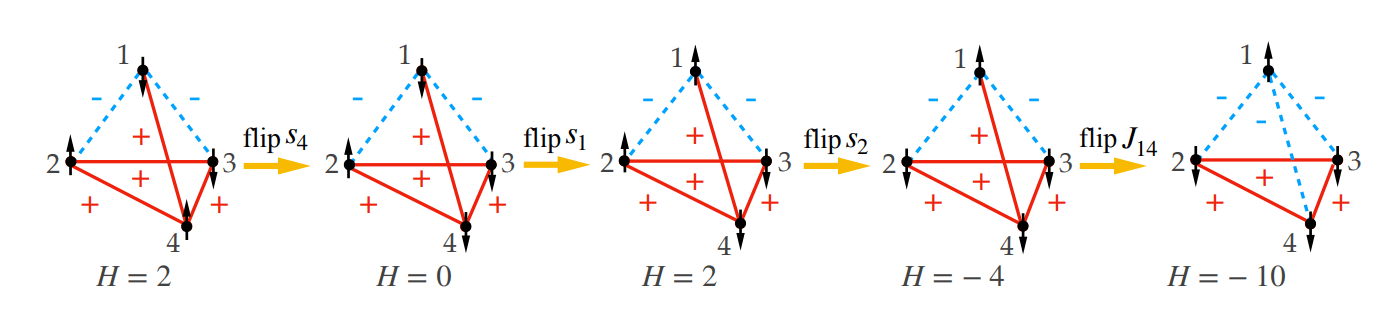
Sample step

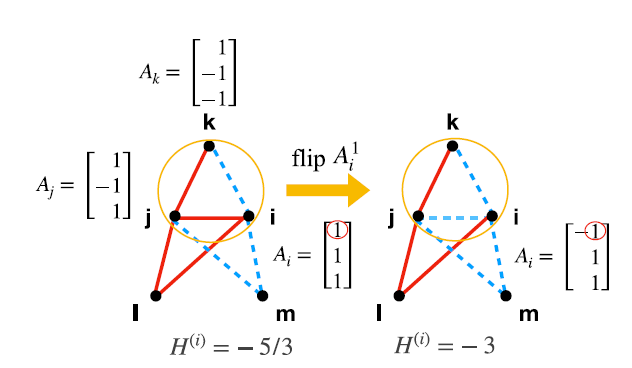
• Here the flip is accepted even if it decreases number of balanced triangles

Phase diagram

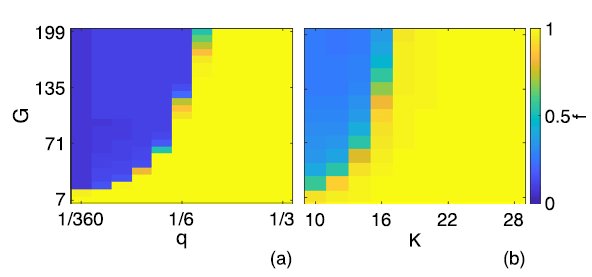
• For large enough \(q\) and degree \(k\) the system reachs stationary, balanced, and fragmented state

Is social balance an emergent phenomenon?

[3]  PNAS (2022) 119 (6) e2121103119

• In many real-world social systems, the tendency to create balanced triangles has been verified
• However, it is questionable whether the individuals can follow all possible triangles to adjust their opinions
• Particularly, this is not realistic on social networks where individuals have hundreds (or thousands) of friends
• So the question is whether the social balance is not just an emergent statistical phenomenon that arises as a consequence of dyadic interactions

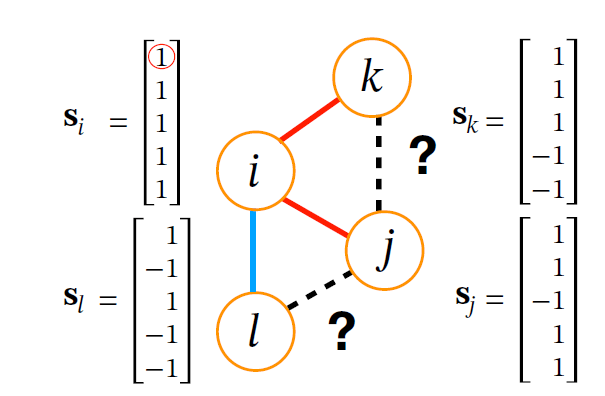
Is social balance in homophily framework

• Individual \(i\) does not know the relations between other individuals, just to his/her neighbors
• The key aspect is that social balance takes both positive and negative links into account

Local Hamiltonian of social systems

• We consider that individuals do not care about social balance
• However, they do care about their friends as well as their enemies
• Therefore, the individual social stress can be expressed as $$H^i(s) = - \alpha \sum_{j: A_{ij}=1}s_i \cdot s_j + (1-\alpha) \sum_{j: A_{ij}=-1} s_i \cdot s_j$$
• The links are determined from \(A_{ij}= \mathrm{sign}(s_i \cdot s_j)\)
• The first term describes homophily with friends
• The second term describes heterophily with enemies
• The parameter \(\alpha\) weights the importance of friendship versus inimical relations

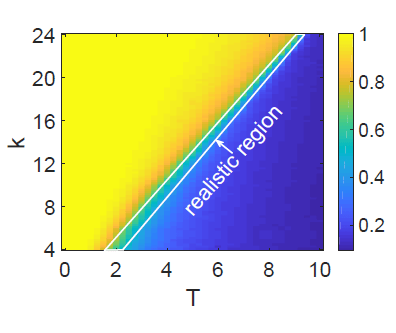
Phase diagram

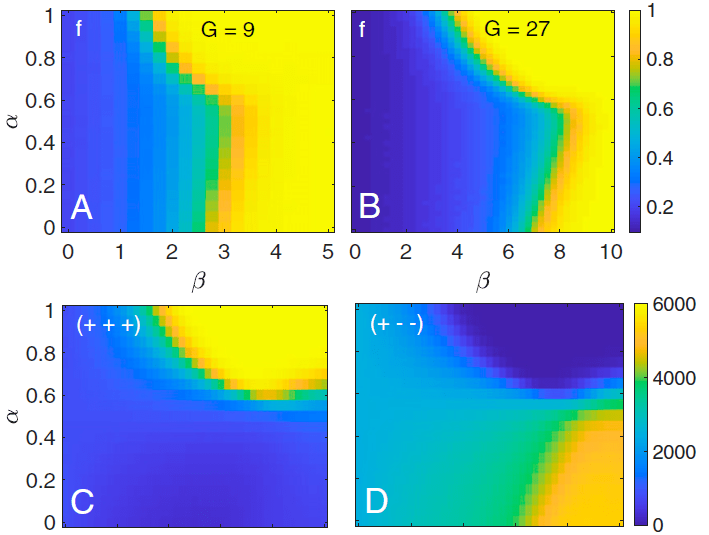
Yellow region - the system is balance (triangles are balanced) - difference between (+ + +) and (+ - - )

Application to PARDUS online game

• Pardus is an online multiplayer game where the players have to cooperate or attack each other to progress
• In the dataset, we can measure the complete network topology as well as if the relation is friendly or hostile

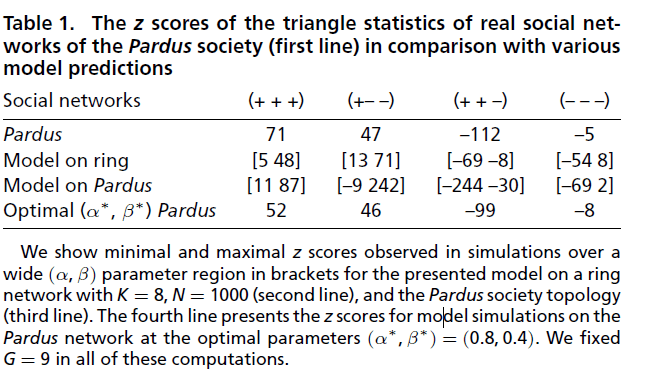
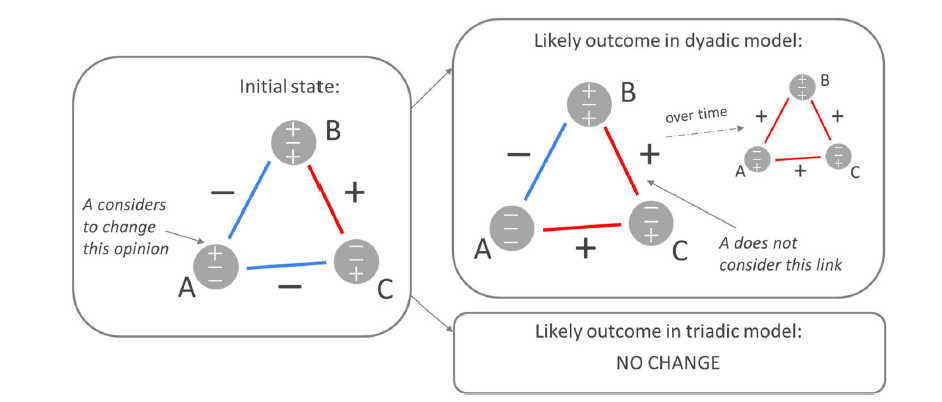
Empirical validation in the social experiment

[4]  npj Complexity 2 (2025) 1

• In a recent study, a team around Mirta Galesic and Henrik Olsson showed the validity of this model in a real-life experiment
• In the longitudinal group experiment with 480 interacting participants, the authors find that
  triadic social balance can be achieved even if people pay attention only to dyadic relationships

Application to to group-size distribution

[5]  Phys. Rev. Lett. 130 (2023) 057401

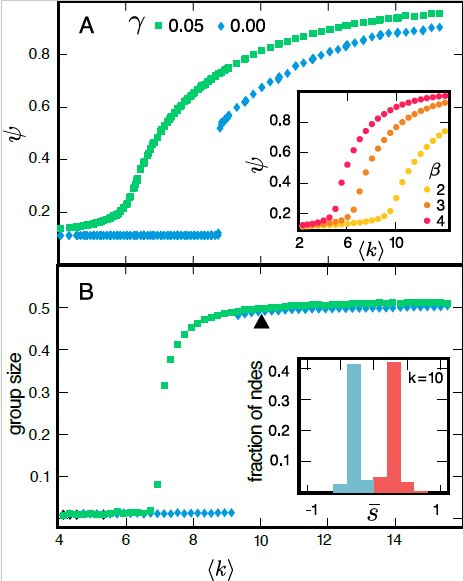
Hamiltonian of a group \(\mathcal{G}\)

\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) =  \textcolor{red}{\underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{intra-group \ social \ stress}} \textcolor{blue}{ + \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{inter-group \ social \ stress}} - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)

Group 1

Group 2

friends

enemies

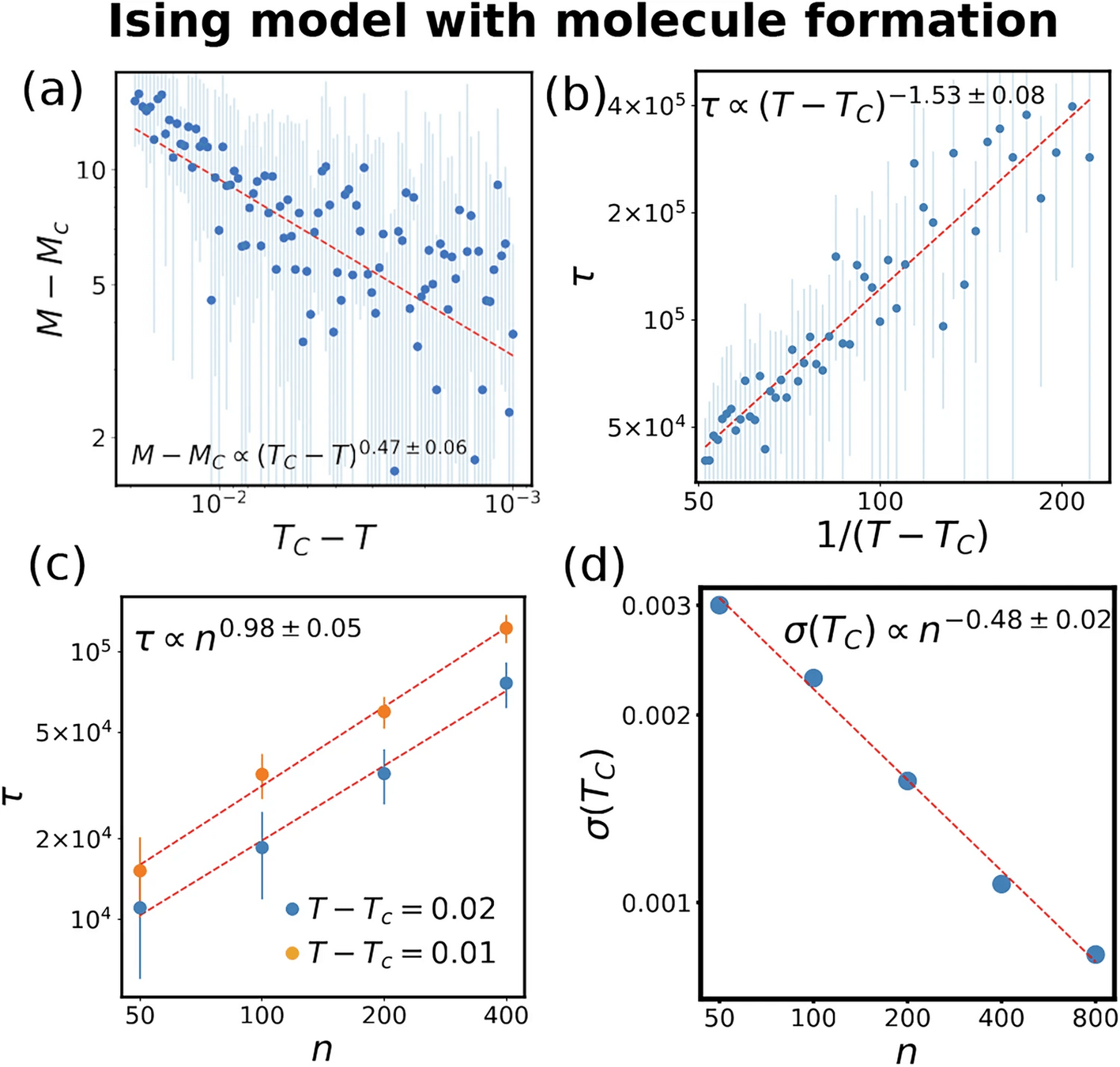
To derive the equilibrium distribution, we extend entropy to systems with emergent structures (molecules, social groups...)

Entropy for structure-forming systems

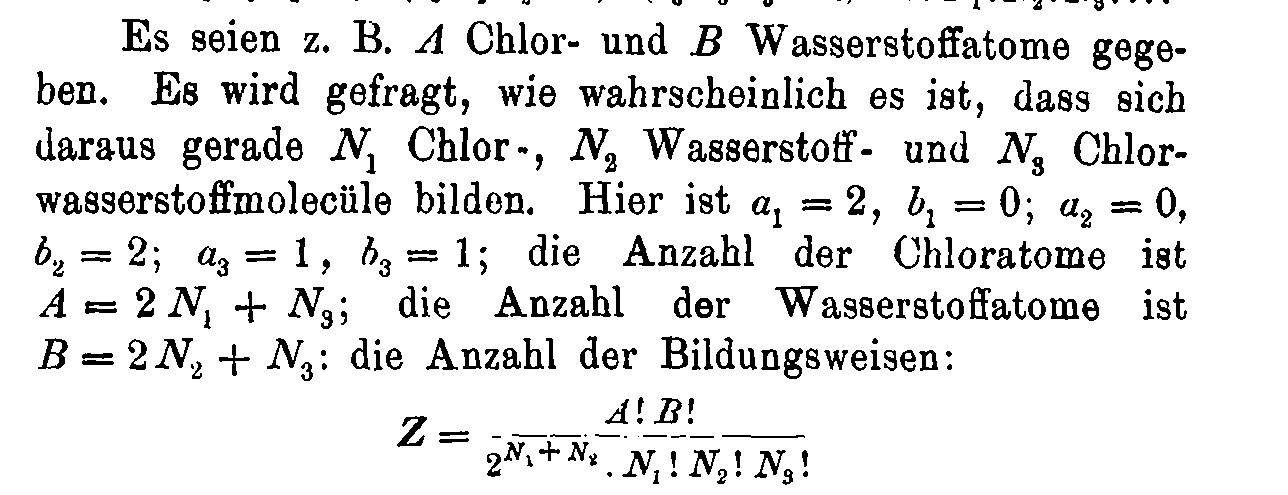
\(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}!  \color{red}(j!)^{n_i^{(j)}}}\)  

$$\mathcal{S} = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log  \frac{j!}{n^{j-1}}}$$

\( S = k \cdot \log W\)

[6]  Nat. Comm. 12 (2021) 1127

MaxEnt distribution

• To calculate the MaxEnt distribution, we maximize the entropy w.r.t. to 
  • normalization \(\sum_{ij} j \wp_{i}^{(j)}=1\)
  • average energy \(\sum_{ij} \wp_{i}^{(j)} \epsilon_{i}^{(j)} = E\)
• Equilibrium distribution: $$\hat{\wp}_i^{(j)} = \frac{n^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$
• Normalization: we solve the equation                                  \(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{n^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{red} \alpha}\)

Model approximations

• Configuration model: We do not know the full network but just a degree distribution.  
  • The probability of observing a link between \(i\) and \(j\) is proportional to \(k_i k_j\)
• Mean-field approximation: We use the mean-field approximation of the Hamiltonian

• These two approximations lead to the set of self-consistency equations:

  $$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$

  where \(q^{(k)}\) is the intra-group degree, \(q^{(k,l)}\) is the inter-group degree and \(P\) is the degree distribution

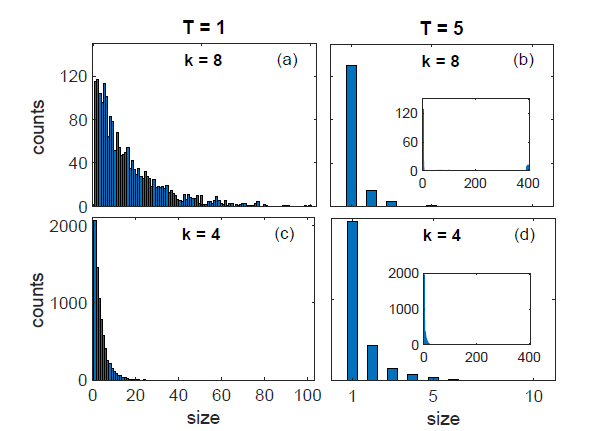
Results for zero intra-group degree

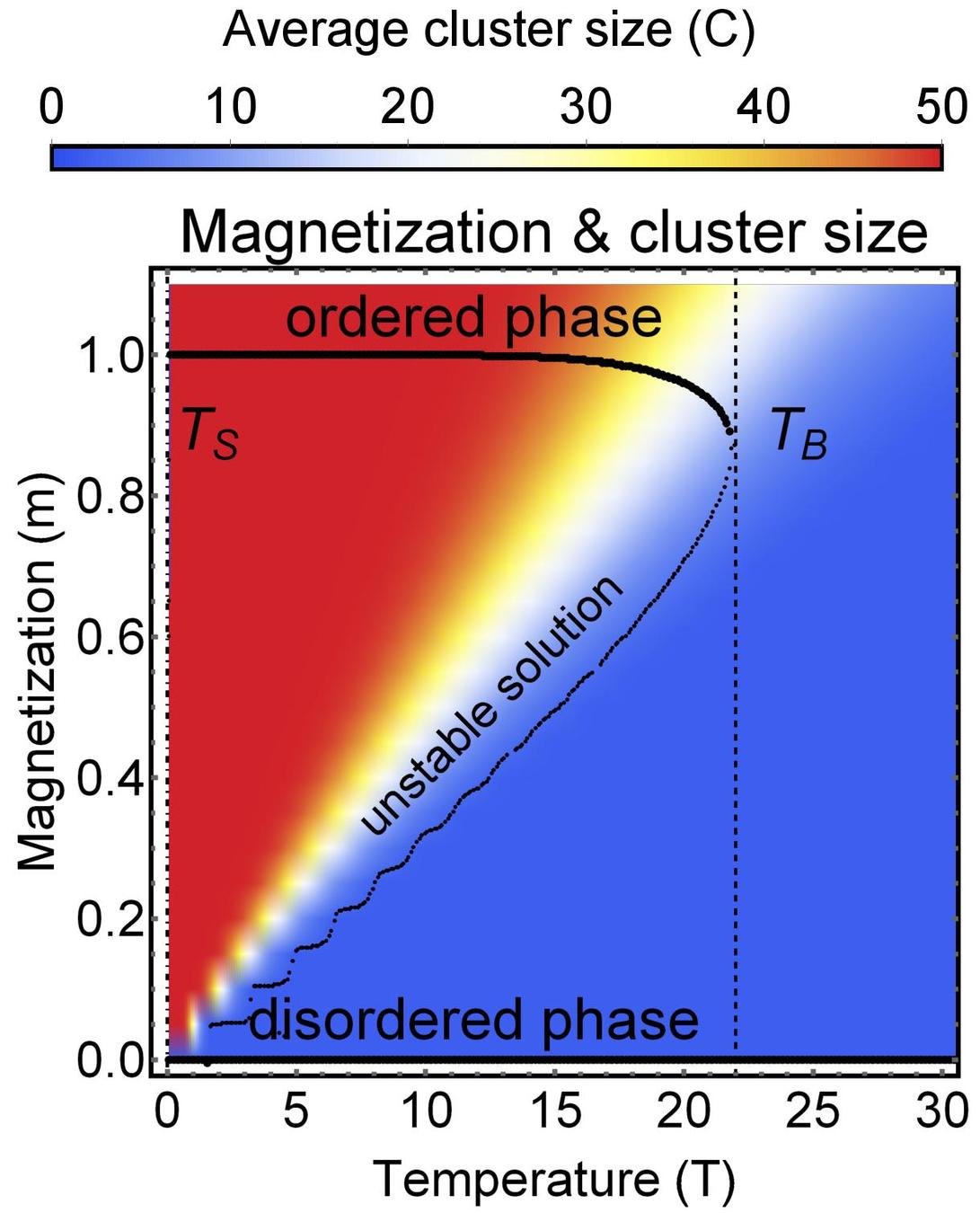
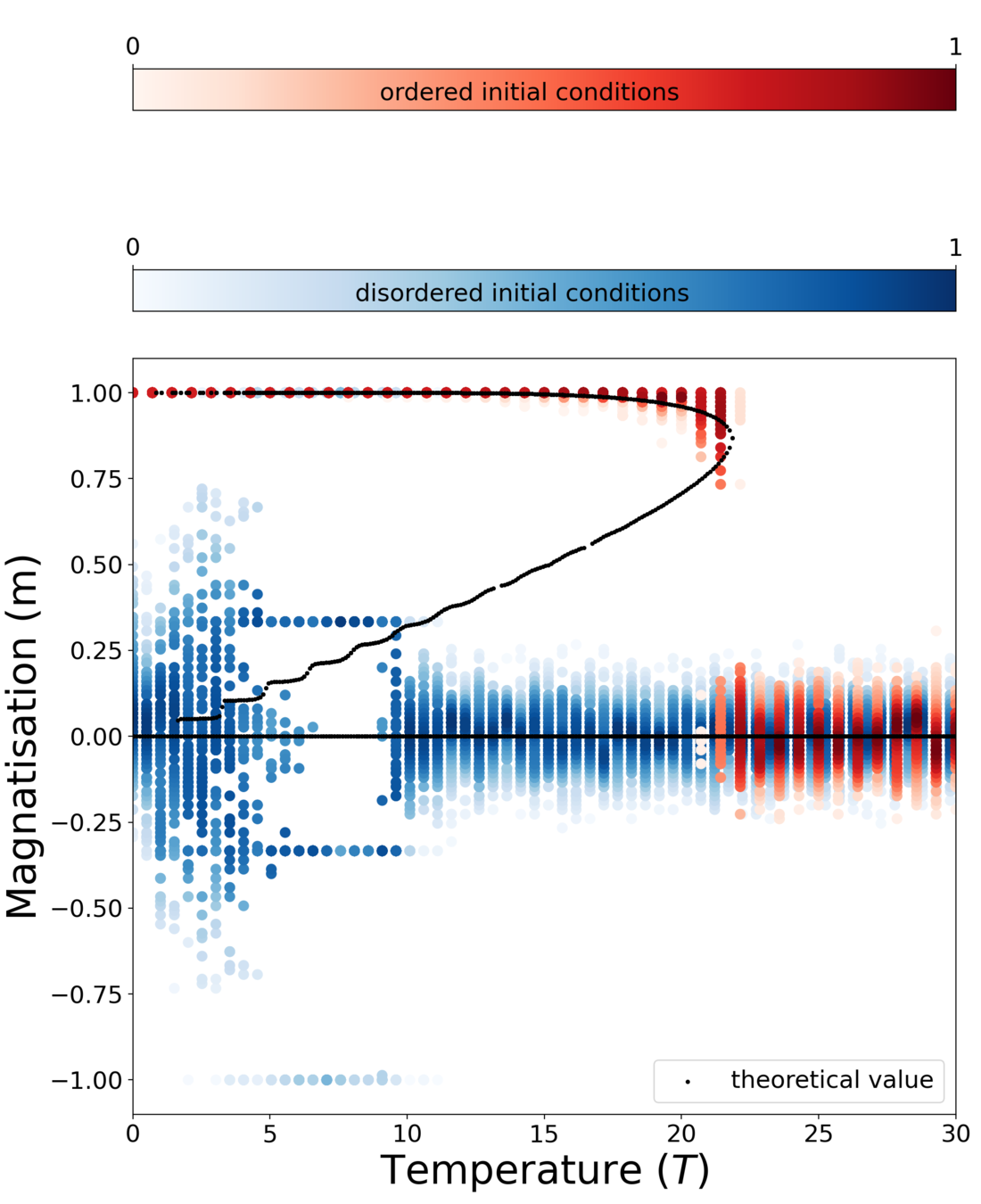
Theory

MC simulation

Pardus group size distribution

Social polarization

[7] to be submitted soon

• Currently, we are investigating how the increase in network connectivity affects polarization
• With the advent of social networks, the average number of connections increased
• We also observe the increase in polarization with the advent of social networks
• Can these two phenomena be explained by the model?

Social polarization

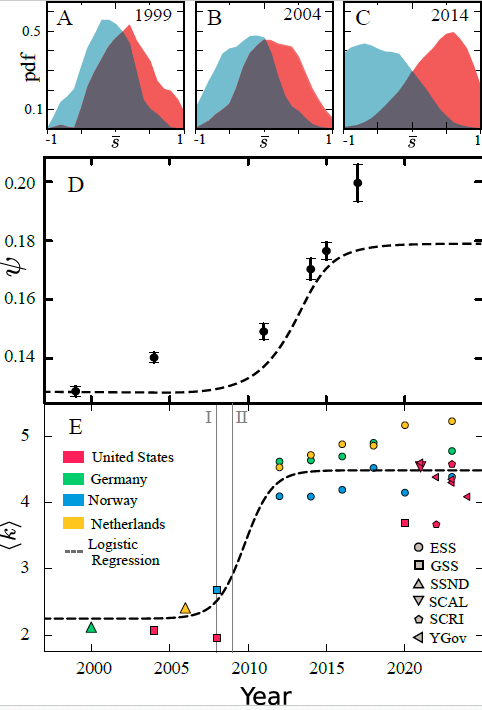
Phase transition in polarization

Future work

[8] Nat. Commun. 16 (2025) 2628

• Recently, we have shown that for a special class of phase transitions that are both first-order (jump) and second-order (criticality), which is called mixed-order transition
• The system exhibits a long plateau at a metastable state before it jumps to another phase

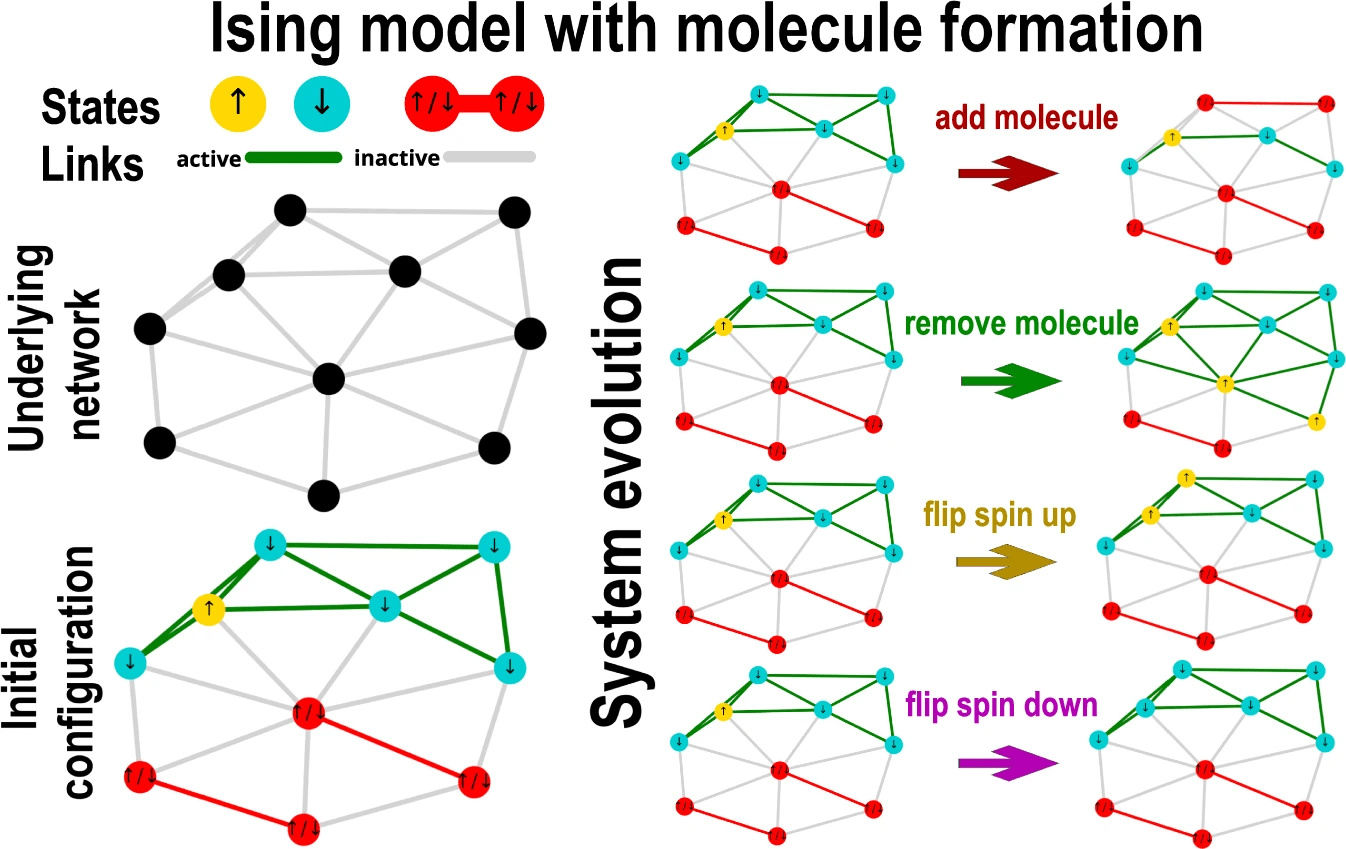
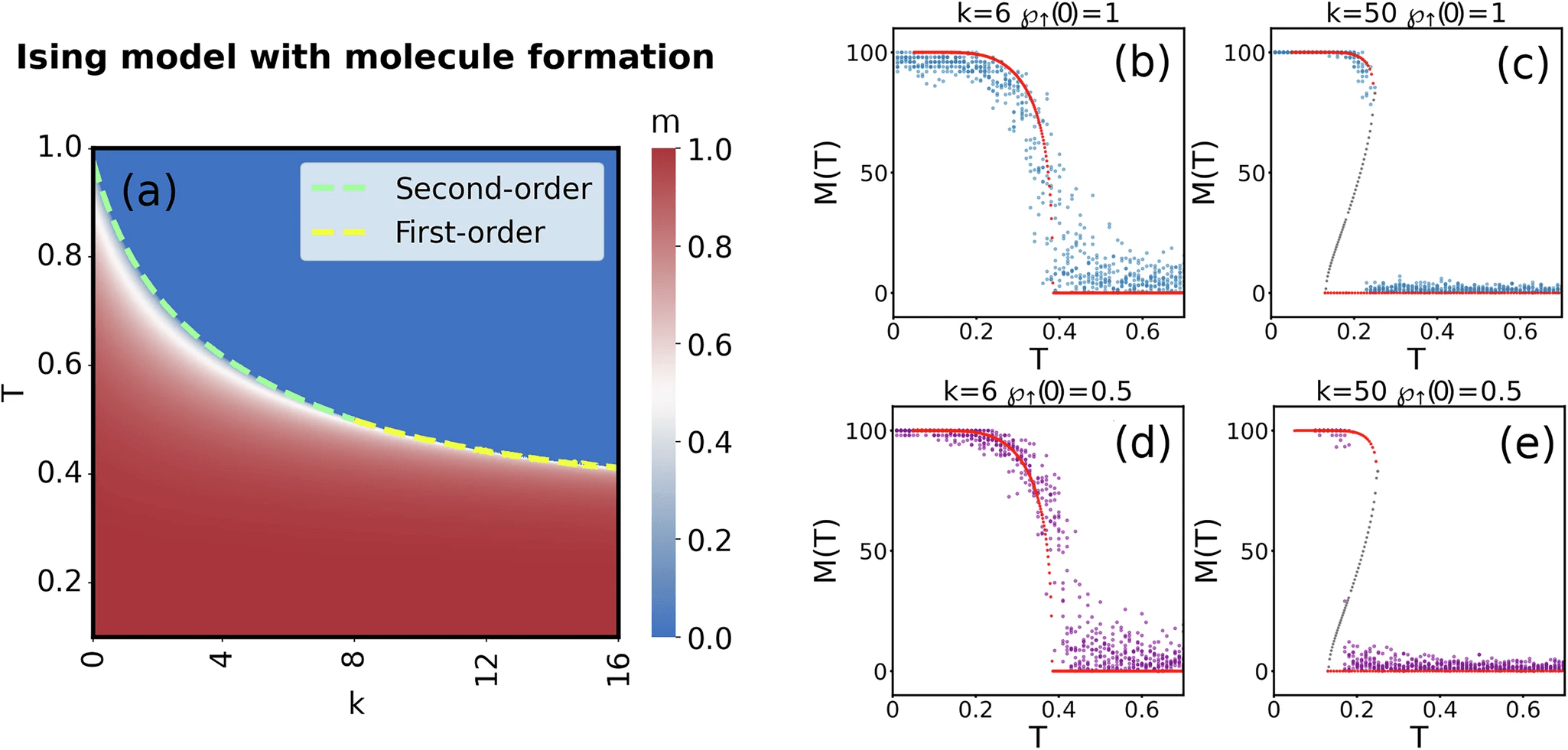
Future work

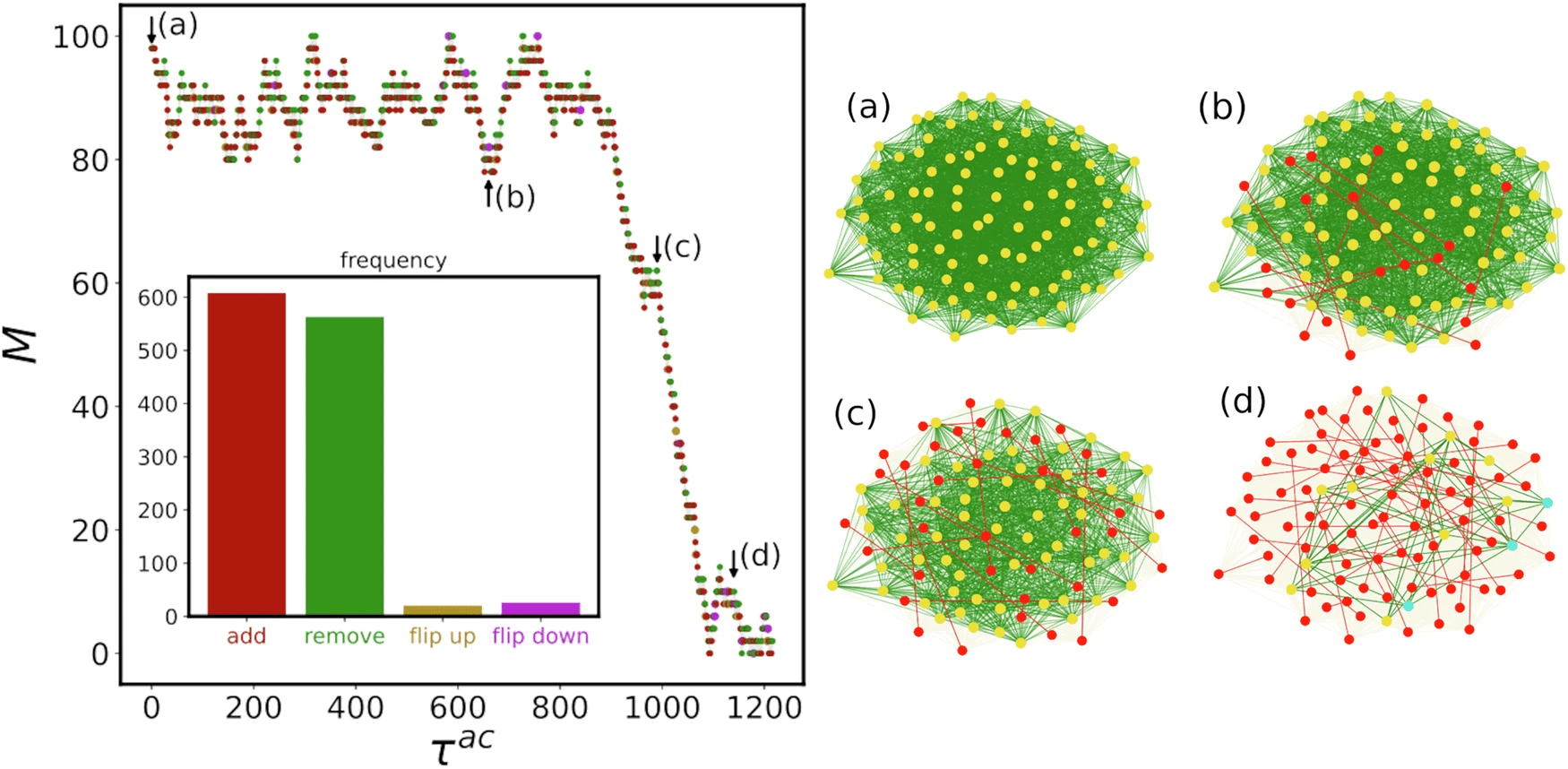
• This behavior is typical for systems with long-range interactions, like social systems
• Mixed-order transitions correspond to sudden jumps that cannot be easily predicted
• Is it the case of of real social systems?

In collaboration with:

csh.ac.at

Stefan Thurner

Rudolf Hanel

Tuan Pham Minh

Simon Lindner

Markus Hofer

Mirta Galesic

Henrik Olsson

Remah Dahdoul

csh.ac.at

References:

[1] T.P.M., Imre Kondor, R.H., S.T., Journal of Royal Society Interface (2020) 1720200752

[2] T.P.M., Andrew Alexander, J.K., R.H., S.T., Scientific Reports 11 (2021) 17188

[3] T.P.M., J.K. R.H., S.T., PNAS 119 (6) (2022) e2121103119

[4] M.G., H.O., T.P.M., Johannes Sorger, S.T., npj Complexity 2 (2025) 1

[5] J.K., S.L., T.P.M., R.H., S.T. Physical Review Letters 130 (2023) 057401

[6] J.K., S.L., R.H., S.T., Nature Communications 12 (2021) 1127

[7] M.H., J.K., S.T., to be submitted

[8] J.K., Shlomo Havlin, S.T., Nature Communications 16 (2025) 2628