Stochastic Thermodynamics
and Fluctuation Theorems
for Non-Linear Systems


Jan Korbel
David Wolpert
22nd International Symposium on "Disordered Systems:
Theory and Its Applications" (DSS-2022)
slides can be found at: slides.com/jankorbel
Overview
-
Brief overview of stochastic thermodynamics
-
Non-linear stochastic thermodnyamics
Thermodynamics
Microscopic systems
Classical mechanics (QM,...)
Mesoscopic systems
Stochastic thermodynamics
Macroscopic systems
Thermodynamics
Trajectory TD
Ensemble TD
Stochastic Thermodynamics is a thermodynamic theory
for mesoscopic, non-equilibrium physical systems
interacting with equilibrium thermal (and/or chemical)
reservoirs
Statistical mechanics
Historical review of thermodynamics
History
Equilibrium thermodynamics (19 th century)
- Maxwell, Boltzman, Planck, Claussius, Gibbs...
- Macroscopic systems (\(N \rightarrow \infty\)) in equilibrium (no time dependence of measurable quantities - thermoSTATICS)
- General structure of thermodynamics
- Laws of thermodynamics (general)
- Response coefficients (system-specific)
- Applications: engines, refridgerators, air-condition,...


efficiency \(\leq 1-\frac{T_2}{T_1}\)
Heat engine: Carnot cycle

Car engines: 30-50%
History
Laws of thermodynamics
Zeroth law:
Temperature can be measured. $$T_A = T_B \quad \mathrm{if} \quad A \ \mathrm{and} \ B \ \mathrm{are} \ \mathrm{in} \ \mathrm{equilibrium}.$$
First law (Claussius 1850, Helmholtz 1847):
Energy is conserved.
$${\color{aqua} d}U = {\color{orange} \delta} Q - {\color{orange} \delta} W$$ Second law (Carnot 1824, Claussius 1854, Kelvin):
Heat cannot be fully transformed into work. $${ \color{aqua} d} S \geq \frac{{\color{orange} \delta} Q}{T}$$ Third law: We cannot bring the system into the absolute zero
temperature in a finite number of steps. $$ \lim_{T \rightarrow 0} S(T) = 0$$
History
Local equilibrium thermodynamics (1st half of 1900s)
- Onsager, Rayleigh...
- Systems close to equilibrium - linear response theory
- Local equilibrium: subsystems a,b,c are each in equilibrium

Total entropy \(S \approx S^a + S^b + S^c + \dots\)
Entropy production \(\sigma^a = \frac{d S^a}{d t} = \sum_i Y_i^a J_i^a \)
\(Y_i^a\) - thermodynamic forces; \(J_i^a\) - thermodynamic currents
4th Law of thermodynamics (Onsager 1931): \( \sigma = \sum_{ij} L_{ij} \Gamma_i \Gamma_j\)
\(\Gamma_i = Y_i^a - Y_i^b \) - afinity, \(L_{ij}\) - symmetric
Molecular motor: myosin walking on actin filament
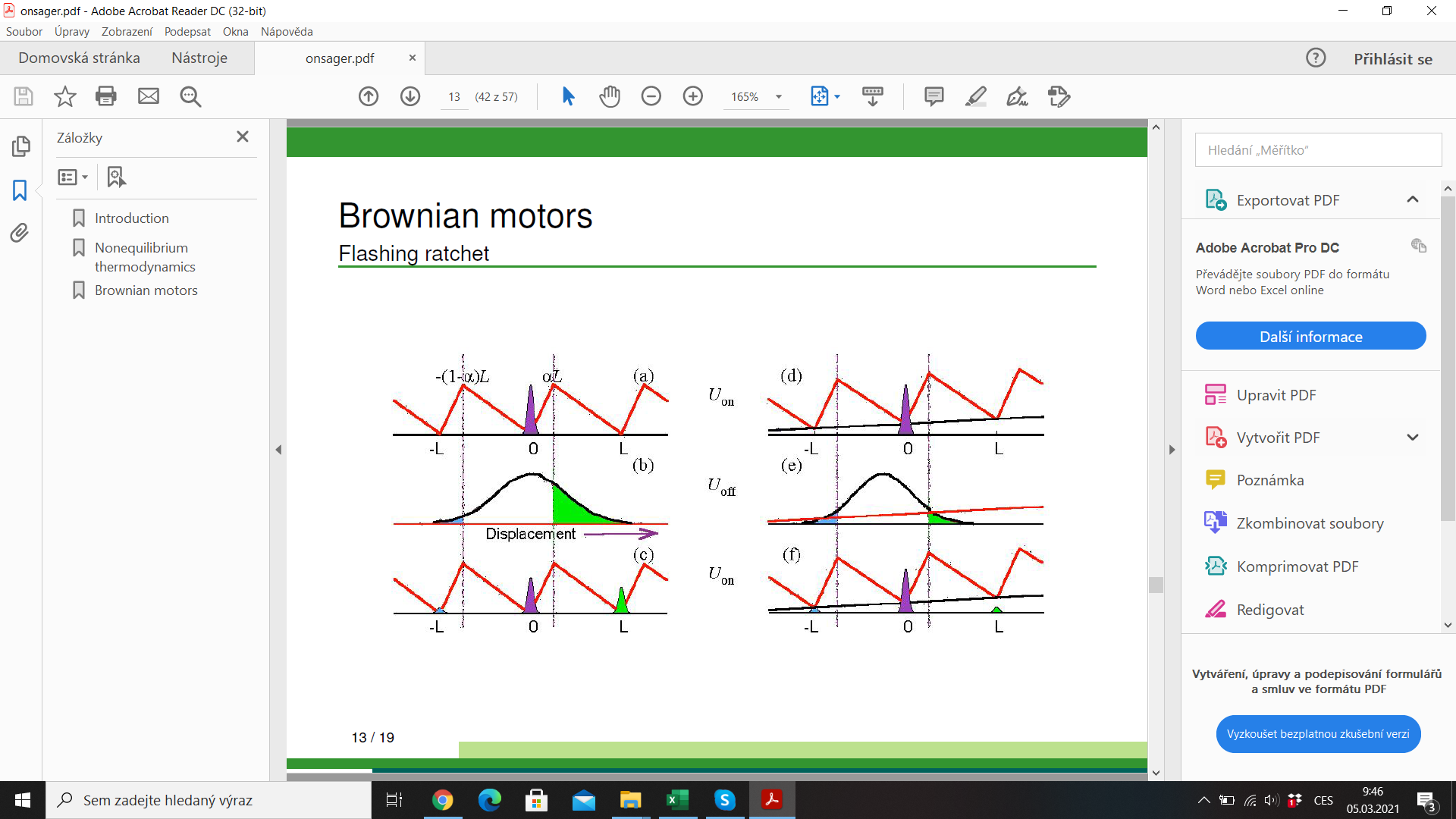
efficiency \(\lesssim 1\)
Main results of stochastic thermodynamics
Stochastic thermodynamics
1.) Consider linear Markov (= memoryless) with distribution \(p_i(t)\).
Its evolution is described by master equation
$$ \dot{p}_i(t) = \sum_{j} [w_{ij} p_{j}(t) - w_{ji} p_i(t) ]$$
\(w_{ij}\) is transition rate.
2.) Entropy of the system - Shannon entropy \(S(P) = - \sum_i p_i \log p_i\). Equilibrium distribution is obtained by maximization of \(S(P)\) under the constraint of average energy \( U(P) = \sum_i p_i \epsilon_i \)
$$ p_i^{eq} = \frac{1}{Z} \exp(- \beta \epsilon_i) \quad \mathrm{where} \ \beta=\frac{1}{k_B T}, Z = \sum_j \exp(-\beta \epsilon_j)$$
Stochastic thermodynamics
3.) Detailed balance - stationary state (\(\dot{p}_i = 0\) ) coincides with the equilibrium state (\(p_i^{eq}\)). We obtain
$$\frac{w_{ij}}{w_{ji}} = \frac{p_i^{eq}}{p_j^{eq}} = e^{\beta(\epsilon_j - \epsilon_i)}$$
4.) Second law of thermodynamics:
$$\dot{S} = - \sum_i \dot{p}_i \log p_i = \frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{p_j}{p_i}$$
$$ =\underbrace{\frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{w_{ij} p_j}{w_{ji} p_i}}_{\dot{S}_i} + \underbrace{\frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{w_{ji}}{w_{ij}}}_{\dot{S}_e}$$
\( \dot{S}_i \geq 0 \) - entropy production rate (2nd law of TD)
\(\dot{S}_e = \beta \dot{Q}\) entropy flow rate
Stochastic thermodynamics
5.) Trajectory thermodynamics - consider stochastic trajectory
\(x(t)= (x_0,t_0;x_1,t_1;\dots)\). Energy \(E_x = E_x(\lambda(t))\), \(\lambda(t)\) - control protocol
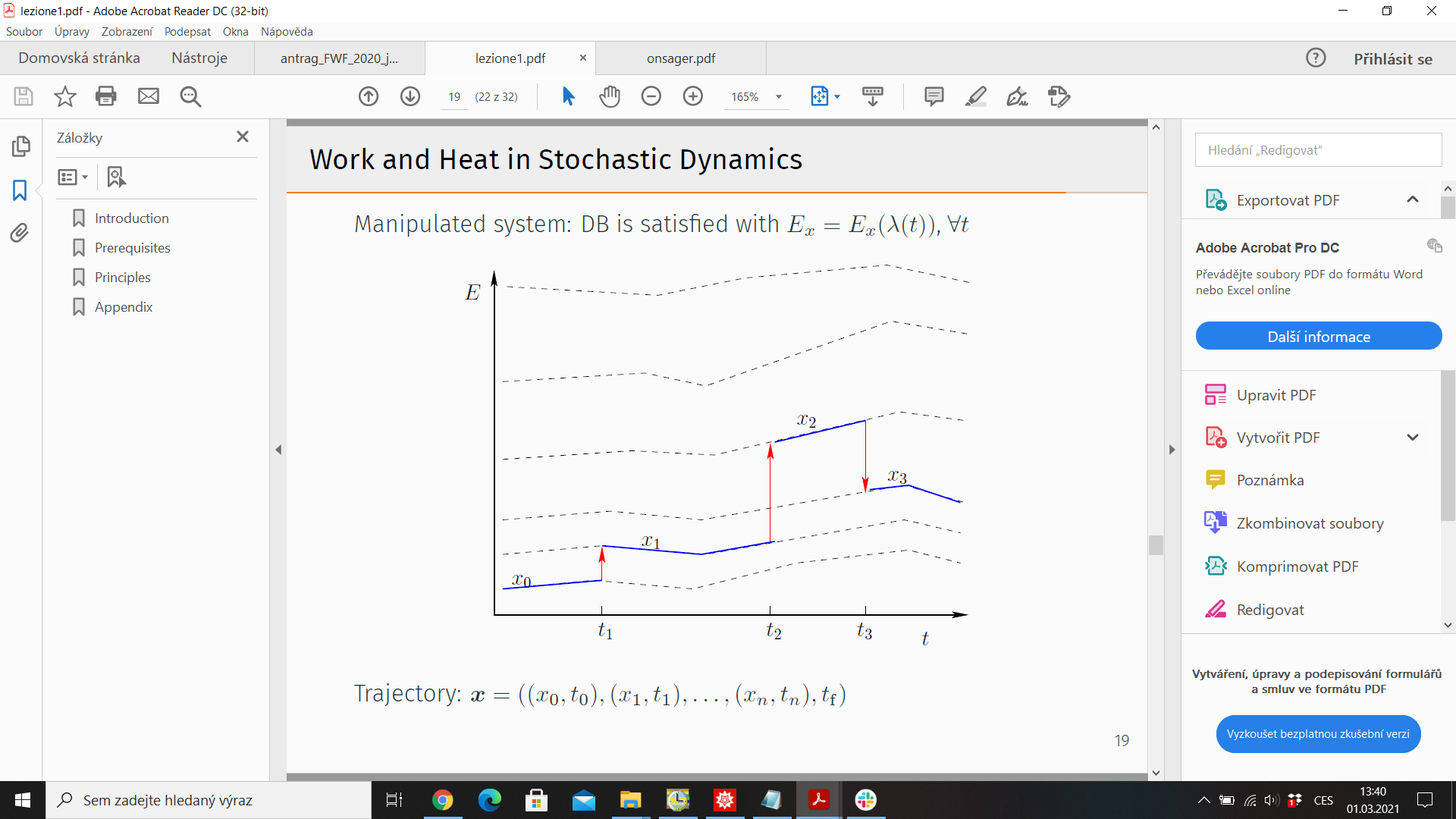
Probability of observing \( x(t)\): \(\mathcal{P}(x(t)\))
Time reversal \(\tilde{x}(t) = x(T-t)\)
Reversed protocol \(\tilde{\lambda}(t) = \lambda(T-t)\)
Probability of observing reversed trajectory under reversed protocol \(\tilde{\mathcal{P}}(\tilde{x}(t))\)
Stochastic thermodynamics
6.) Fluctuation theorems
Trajectory entropy: \(s(t) = - \log p_x(t)\)
Trajectory 2nd law \(\Delta s = \Delta s_i + \Delta s_e\)
Relation to the trajectory probabilities
$$\log \frac{\mathcal{P}(x(t))}{\tilde{\mathcal{P}}(\tilde{x}(t))} = \Delta s_i$$
Detailed fluctuation theorem
$$\frac{P(\Delta s_i)}{\tilde{P}(-\Delta s_i)} = e^{\Delta s_i}$$
Integrated fluctuation theorem $$ \langle e^{- \Delta s_i} \rangle = 1 \quad \Rightarrow \langle \Delta s_i \rangle = \Delta S_i \geq 0$$
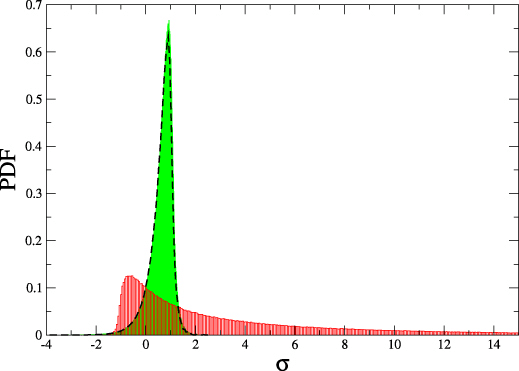
Stochastic thermodynamics for non-linear systems
Stochastic thermodynamics of non-linear systems
(with D. Wolpert - New J. Phys. doi:10.1088/1367-2630/abea46)
- Many complex, long-range systems are non-linear
- Question: can we use stochastic thermodynamics?
Requirements:
- Non-linear Markov dynamics $$ \dot{p}_i(t) = \frac{1}{C(p)} \sum_{j} [w_{ij} \Omega(p_{j}(t)) - w_{ji} \Omega(p_i(t)) ]$$
- Detailed balance $$\frac{w_{ij}}{w_{ji}} = \frac{\Omega(p_i^{eq})}{\Omega(p_j^{eq})} $$
- Second law of thermodynamics:
- For some (generalized) entropy : \(\dot{S}_i \geq 0\).
Generalized entropies
-
Studied in information theory since 60'S
-
used in physics since 90's
-
Main aim: study thermodynamics of systems with non-Botlzmannian equilibrium distributions (due to correlations, long-range interactions...)
-
We consider a sum-class form of entropy:
\( S(P) = f\left(\sum_m g(p_m) \right) \)
-
Maximum entropy principle: Maximize S(p) subject to constraint that p is normalized and expected energy has a given value
Solution: MaxEnt distribution: \( p^\star_m = (g')^{-1} \left(\frac{\alpha+\beta \epsilon_m}{C_f} \right) \),
\( C_f = f'(\sum_m g(p_m)) \)
Theorem: Requirements 1-3 imply
1) \(\Omega(p_m) = \exp(-g'(p_m))\)
2) \(C(p) = f'(\sum_m g(p_m))\)
Generalized entropies for non-linear systems
Corollary:
a) \(S(p) = f\left(-\sum_m \int_0^{p_m} \log \Omega(z) \mathrm{d} z \right) \)
b) \(\frac{w_{mn}}{w_{nm}} = \frac{\epsilon_m-\epsilon_n}{T}\)
Sketch of proof
\( \dot{S} = C_f \sum_m \dot{p}_m g'(p_m) \)
\(= \frac{C_f}{2} \sum_{mn} (J_{mn}-J_{nm}) (g'(p_m) - g'(p_n)) \)
\( = \frac{C_f}{2} \sum_{mn} (J_{mn}-J_{nm}) (\Phi_{mn} - \Phi_{nm}) \)
\(+ \frac{C_f}{2} \sum_{mn} (J_{mn}-J_{nm}) (g'(p_m)+\Phi_{nm} - g'(p_n) - \Phi_{mn}) \)
\( = \underbrace{\frac{C_f}{2} \sum_{mn} (J_{mn}-J_{nm}) (\phi(J_{mn}) - \phi(J_{nm}) )}_{\dot{S}_i}\)
\(+ \underbrace{\frac{C_f}{2} \sum_{mn} (J_{mn}-J_{nm}) (g'(p_m)+\phi(J_{nm}) - g'(p_n) - \phi(J_{mn}) )}_{\dot{S}_e} \)
Sketch of proof
\(\dot{S}_i \Rightarrow \phi - \ increasing\)
\(\dot{S}_e \Rightarrow C_f[g'(p_m) + \phi(J_{nm}) - g'(p_n) - \phi(J_{mn})] = \frac{\epsilon_n - \epsilon_m}{T} \)
\(\Rightarrow \phi(J_{mn}) = j(w_{mn}) - g'(p_n) \)
\(\Rightarrow J_{mn} = \psi(j(w_{mn}) - g'(p_n))\), \( \psi = \phi^{-1} \) - increasing \( \square . \)
Notes:
\( j(w_{mn}) - j(w_{nm}) = \frac{\epsilon_n - \epsilon_m}{C_f T} \)
\( \beta = \frac{1}{T} \)
analogous for multiple heat baths
Consequences and applications
- Similar result can be derived for continuous spaces - non-linear Fokker-Planck equation $$ \partial_t p(x,t) = - \partial_x \left[ u(x,t) \Omega(p(x,t)) + D(x,t) \Omega(p(x,t)) \partial_x g'(p(x,t)) \right]$$
- Examples:
- \(g(p_m) \propto p_m^q\) (CRN, finance)
- \(g(p_m) = p_m \log p_m + (1-p_m) \log (1-p_m)\) (FD, turbulence)
- \(g(p_m) = p_m \log (p_m/(1+\alpha p_m))\) (negative feedback)
Stochastic entropy: \(s(t) = \log\left(\frac{1}{\Omega(p_x(t))}\right) = g'(p_x(t))\)
Detailed fluctuation theorem holds:
$$\frac{P(\Delta s_i)}{\tilde{P}(-\Delta s_i)} = e^{\Delta s_i}$$
Summary
- There is a link between non-linear dynamics and thermodynamics of generalized entropies
- The connection is determined by the local detailed balance and the second law of thermodynamics
- The connection work for discrete systems (master equation) as well as for continuous systems (Fokker-Planck equation)
- Detailed fluctuation theorem has the regular form
Stochastic thermodynamics of non-linear systems
By Jan Korbel
Stochastic thermodynamics of non-linear systems
- 352



