Homophily-Based Social Group Formation
in a Spin Glass Self-Assembly Framework




in collaboration with
Simon Lindner
Tuan Pham
Rudolf Hanel
Stefan Thurner
Journal Ref.: Phys. Rev. Lett. 130 (2023) 057401
Slides available at: www.slides.com/jankorbel

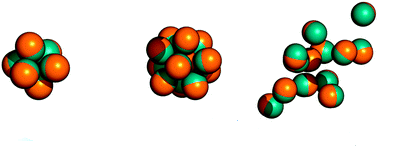
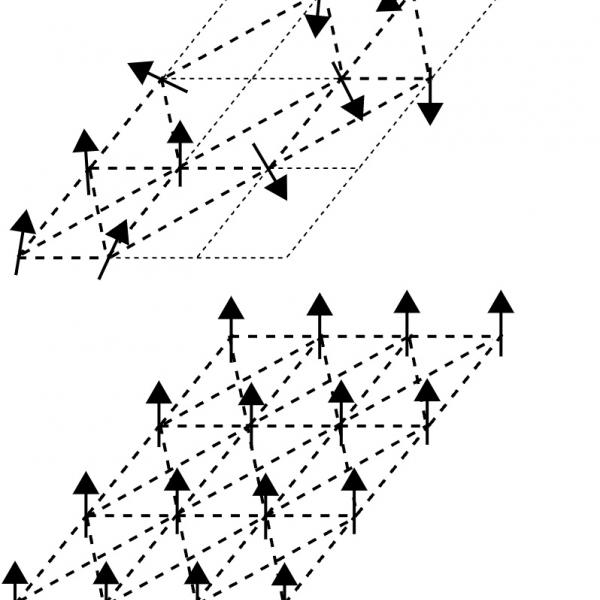
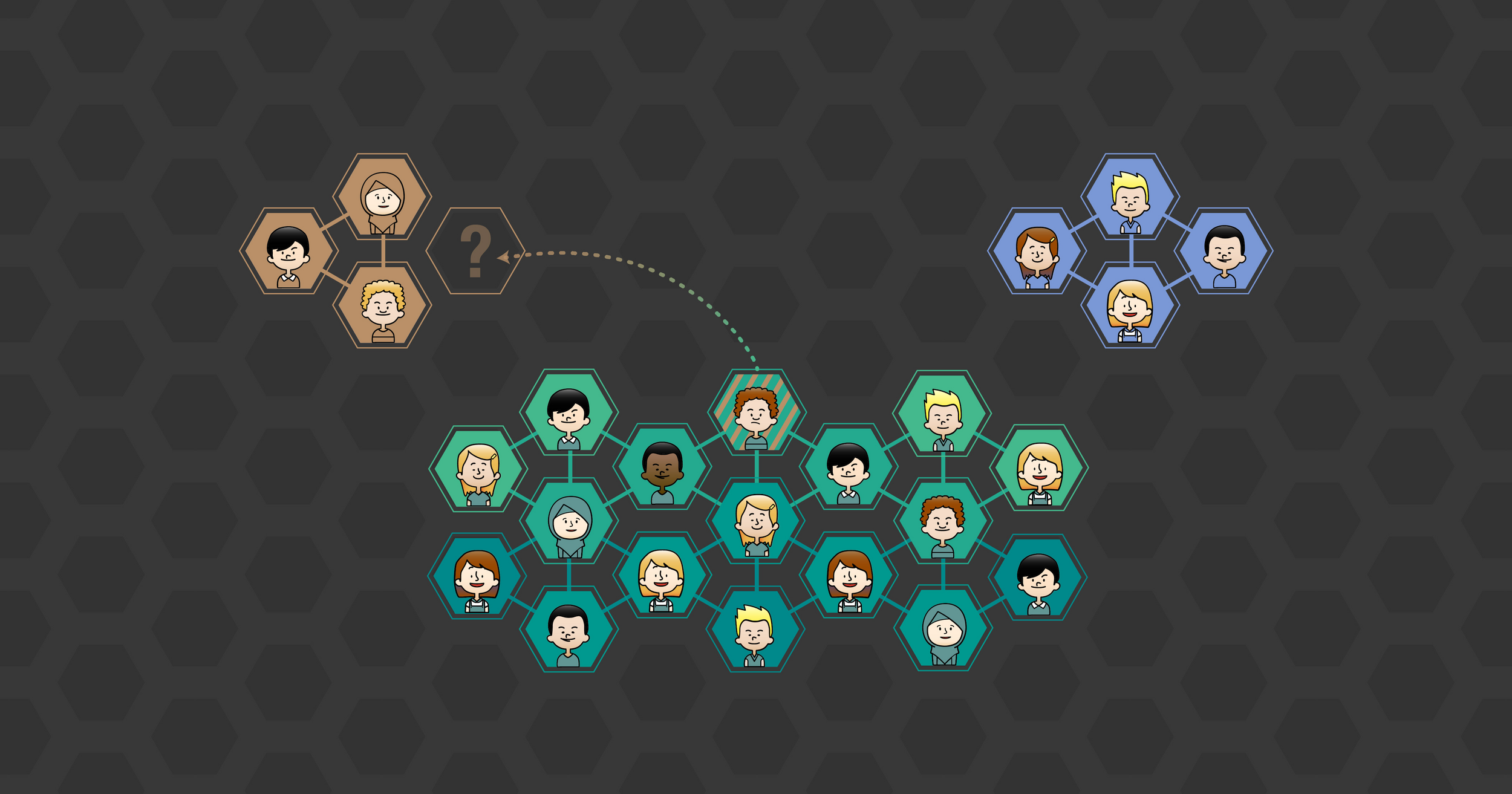
Graphical abstract
1. soft-matter self-assembly
2. condensed matter spin glasses
3. social group formation
Paper flow



1.
2.
3.
1. Thermodynamics of
structure-forming systems
Entropy for systems with structures

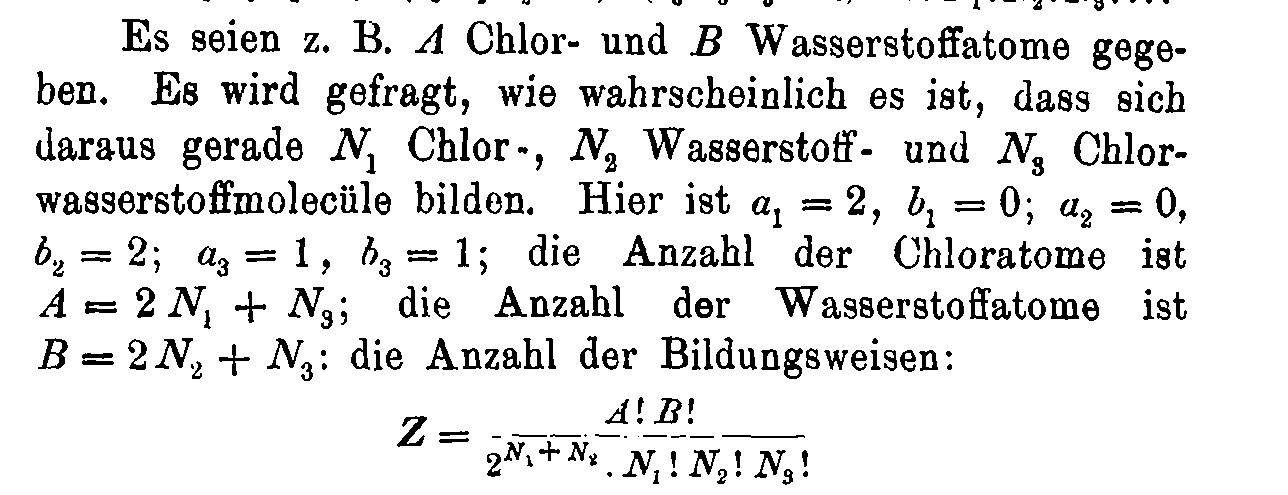
\(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}! (j!)^{n_i^{(j)}}}\)
$$\mathcal{S} = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{n^{j-1}}}$$

\( S = k \cdot \log W\)
Applications to self-assembly
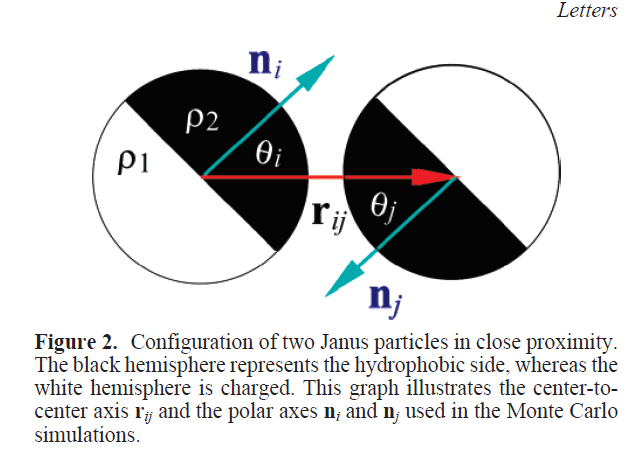

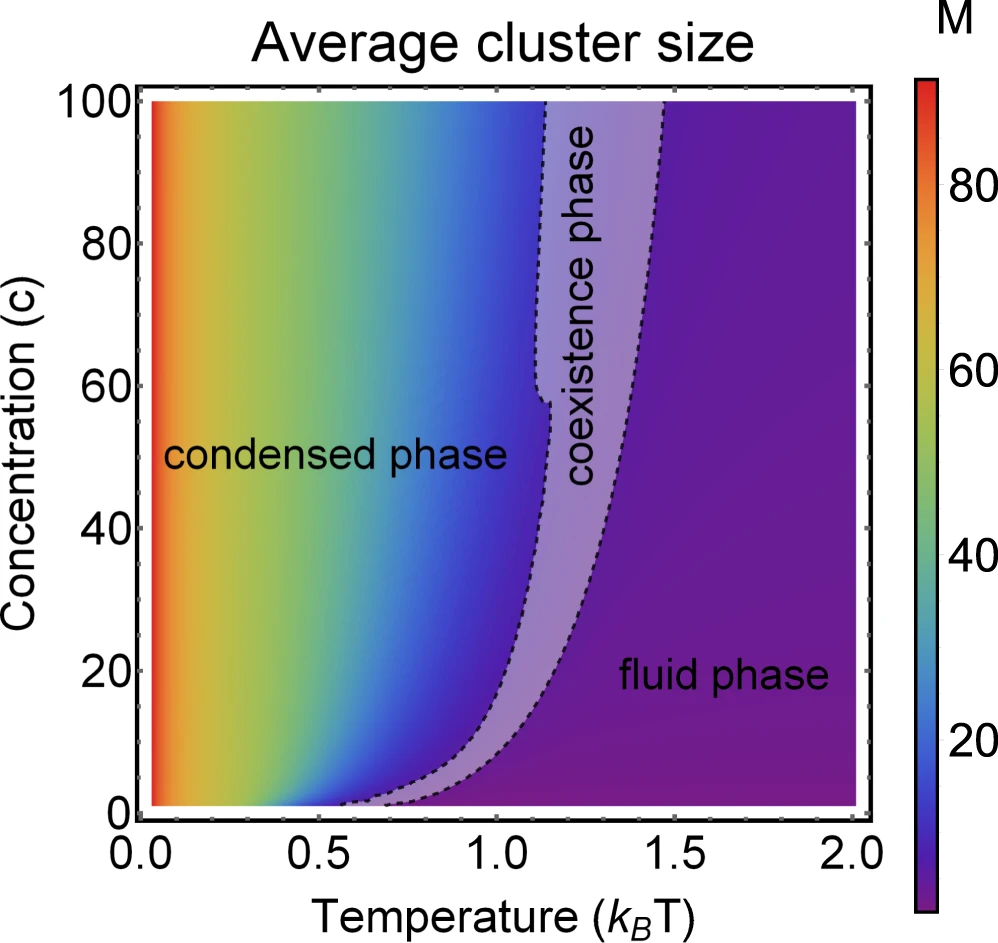
2. Spin-glass based opinion dynamics
- Many opinion dynamics systems follow two basic concepts:
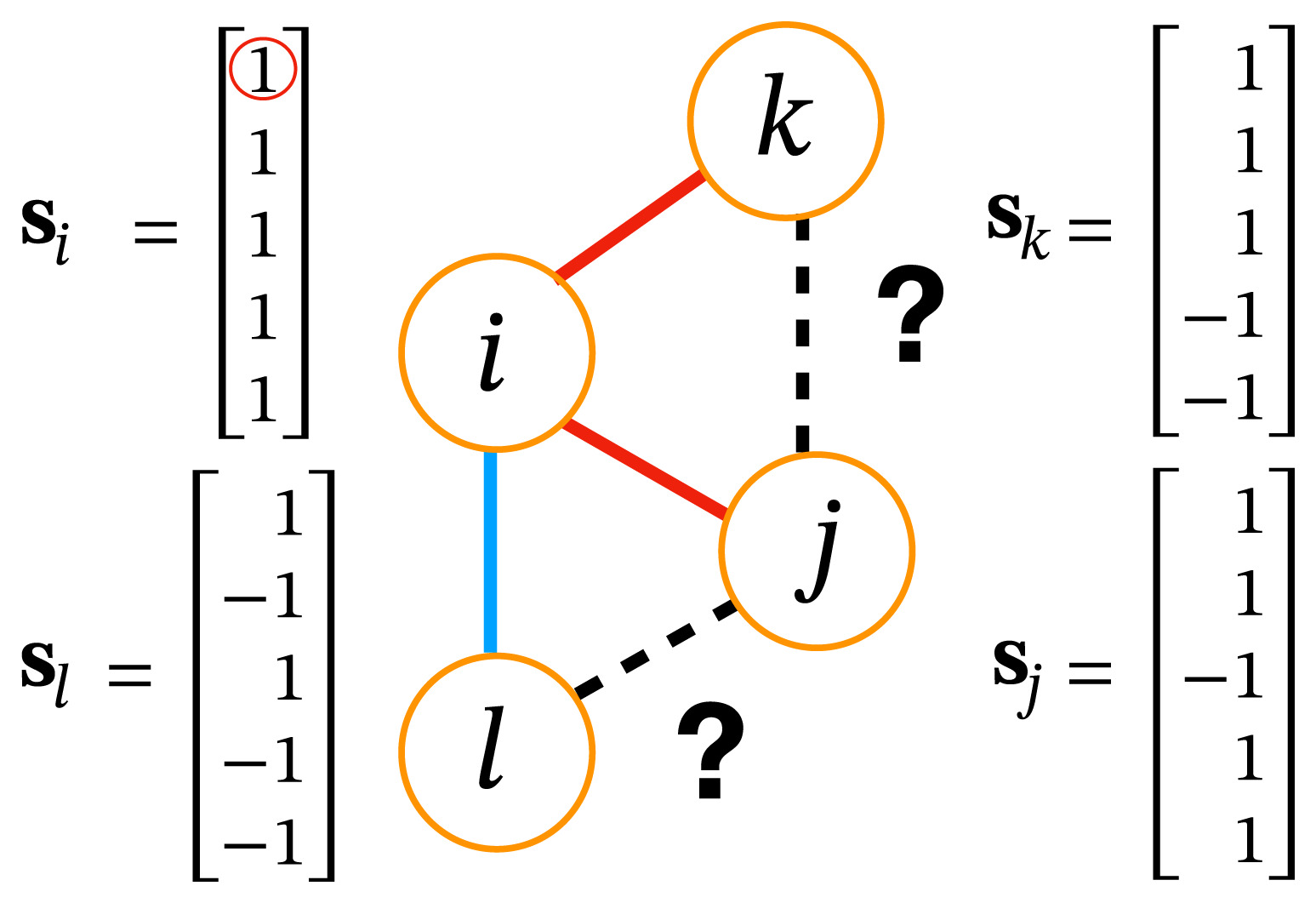
- Homophily - people tend to be friends with peers with similar opinions
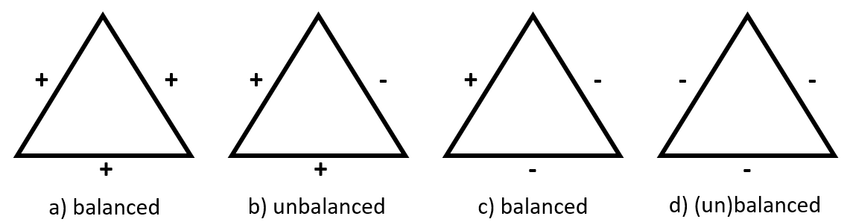
- Social balance - a friend of my friend is my friend, enemy of my friend is my enemy
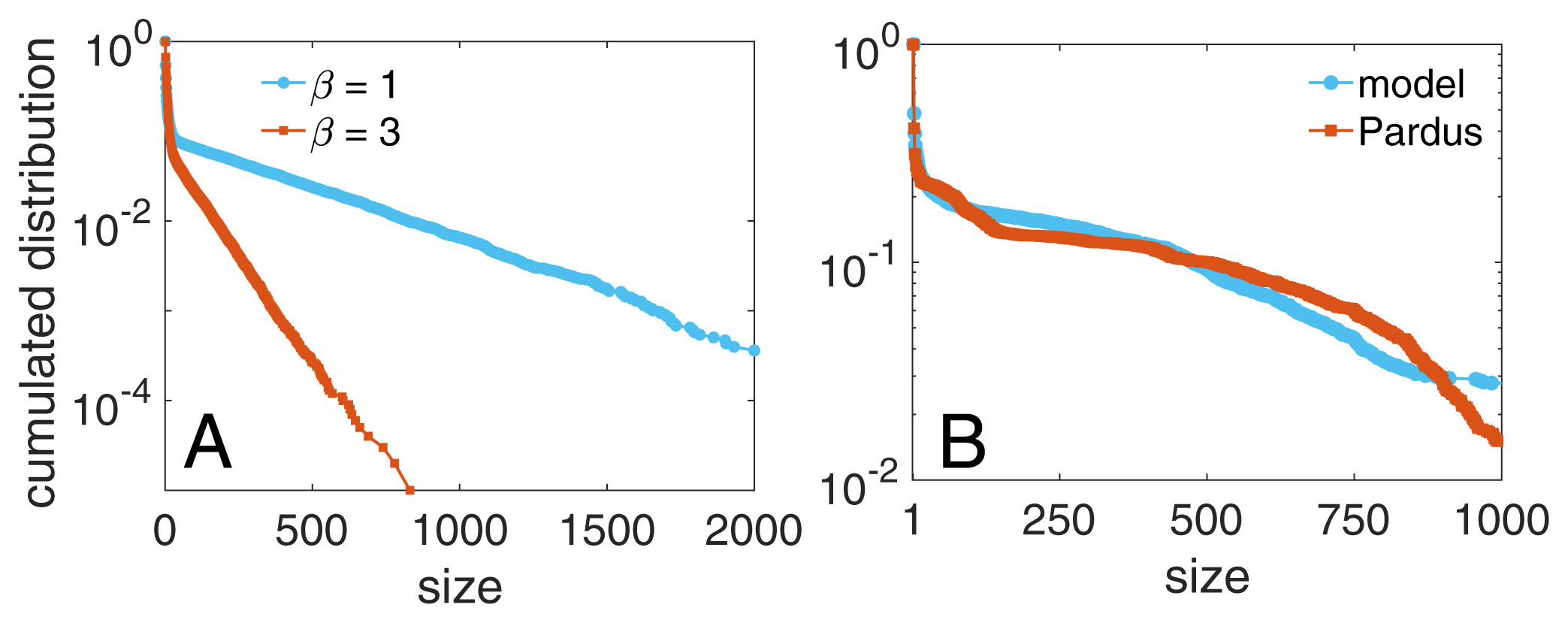
Group size distribution
Social balance emerges from homophily
3. Social group formation in the spin-glass self-assembly framework
Hamiltonian of a group \(\mathcal{G}\)
\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) = \textcolor{red}{\underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{intra-group \ social \ stress}} \textcolor{blue}{ + \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{inter-group \ social \ stress}} \\ \qquad \qquad \qquad \qquad - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)
Group formation based on opinion= self-assembly of spin glass
Group 1
Group 2
friends
enemies
Approximations used in the model
1. Simulated annealing
- We do not know the full network but just a degree distribution. \(\Rightarrow\) The probability of observing a link between \(i\) and \(j\) is proportional to \(k_i k_j\)
2. Mean-field approximation
- We use the mean-field approximation of the Hamiltonian
\(\Rightarrow\) \(m^{(k)} = \sum_{i \in group \ of \ size \ k} s_i\) - average opinion vector of a group of size \(k\)
These two approximations lead to the set of self-consistency equations:
$$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$
where \(q^{(k)}\) is the intra-group degree, \(q^{(k,l)}\) is the inter-group degree and \(P\) is the degree distribution
Results for zero inter-group degree
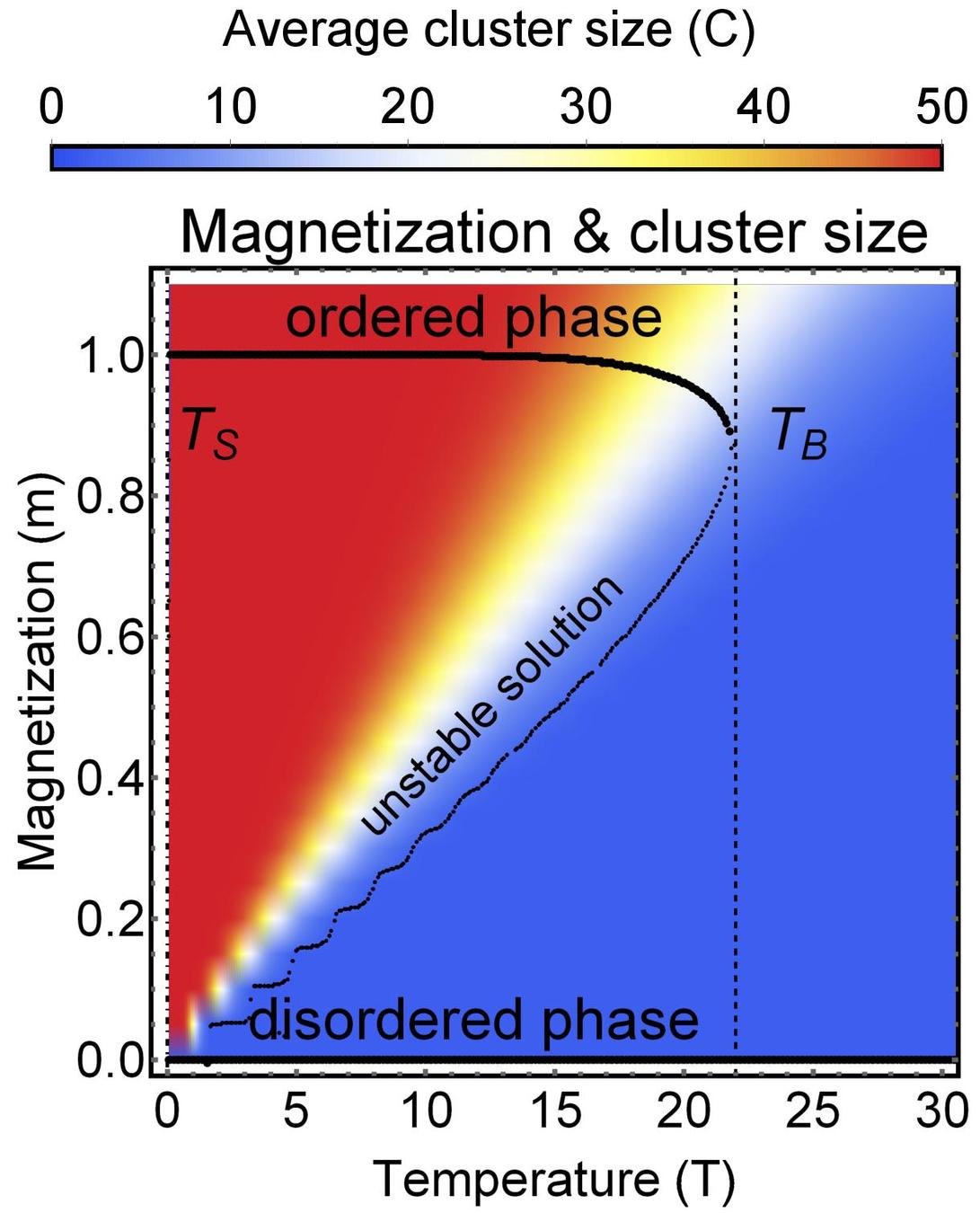
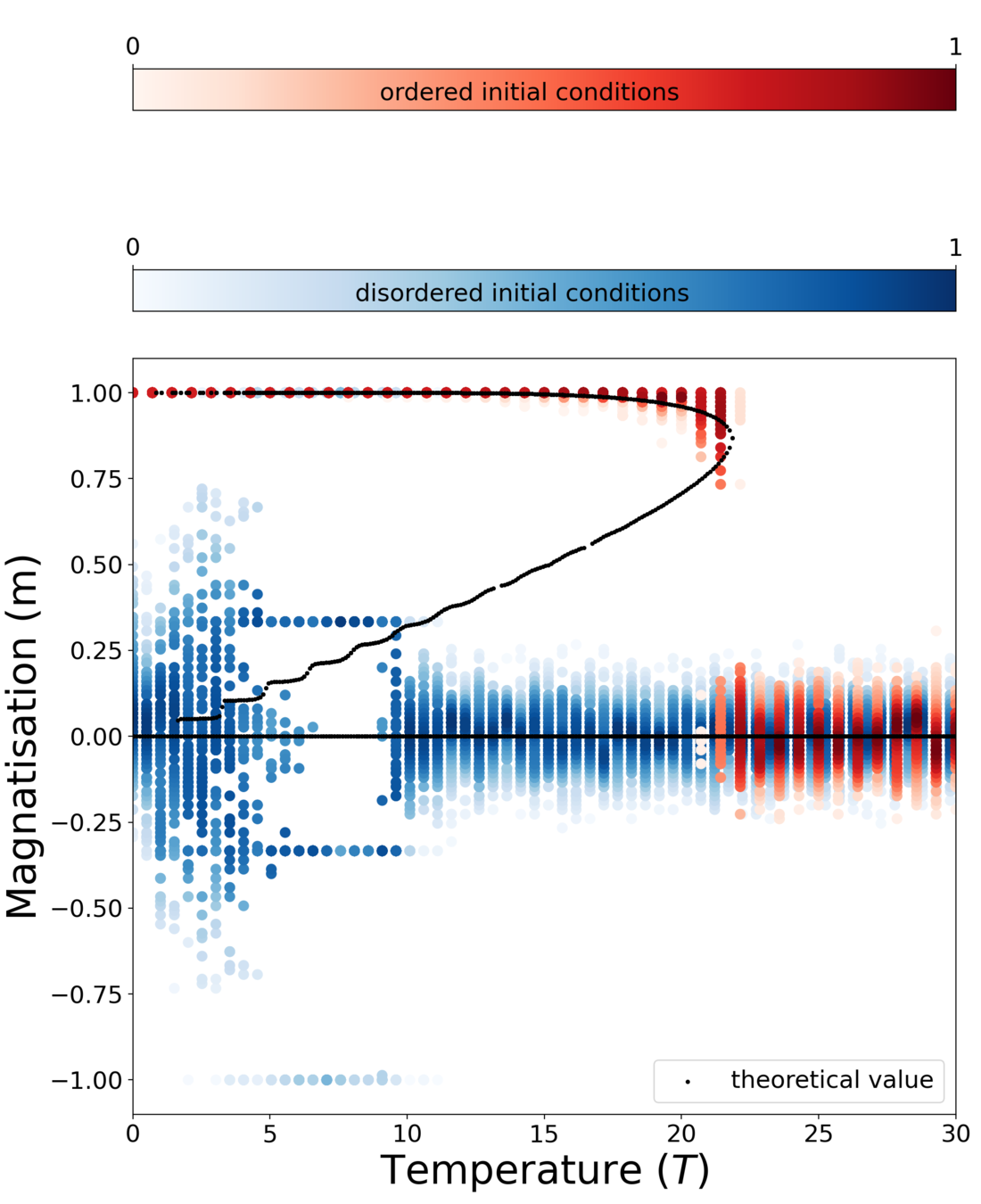
Theory
MC simulation
Dependence on external field
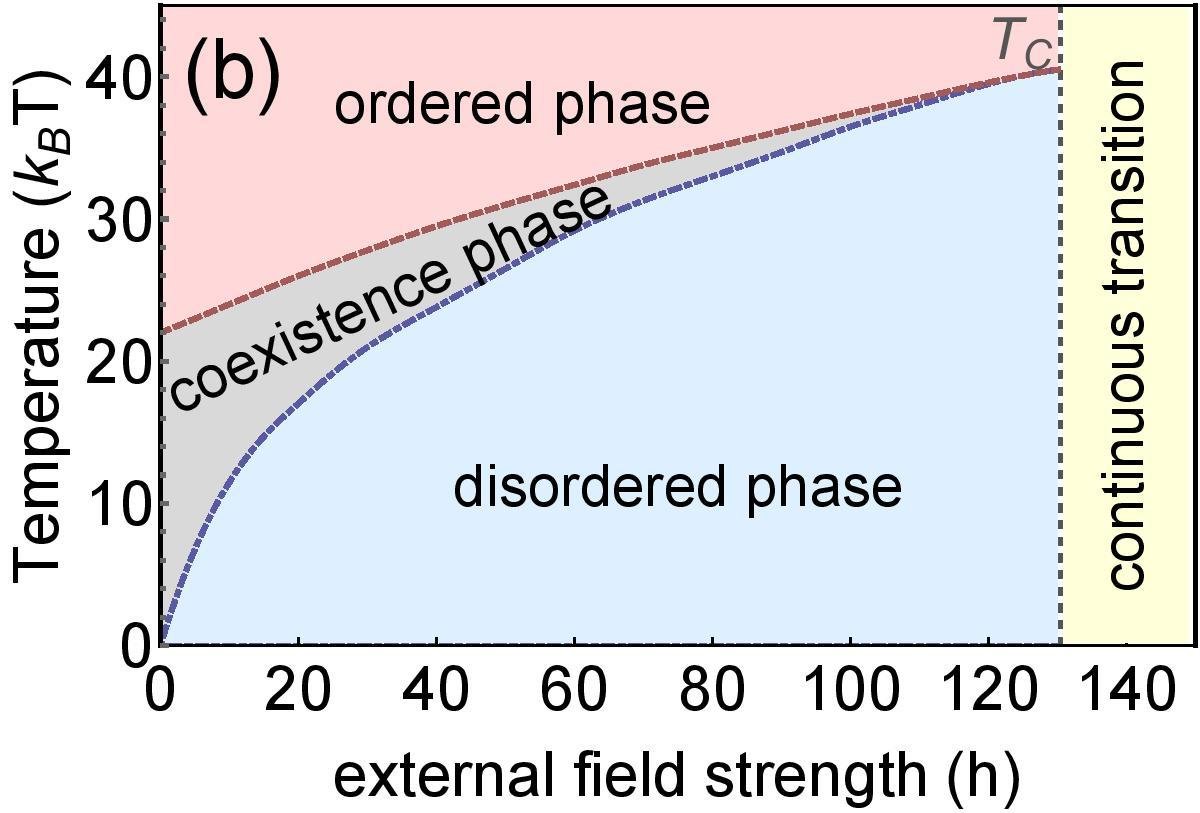
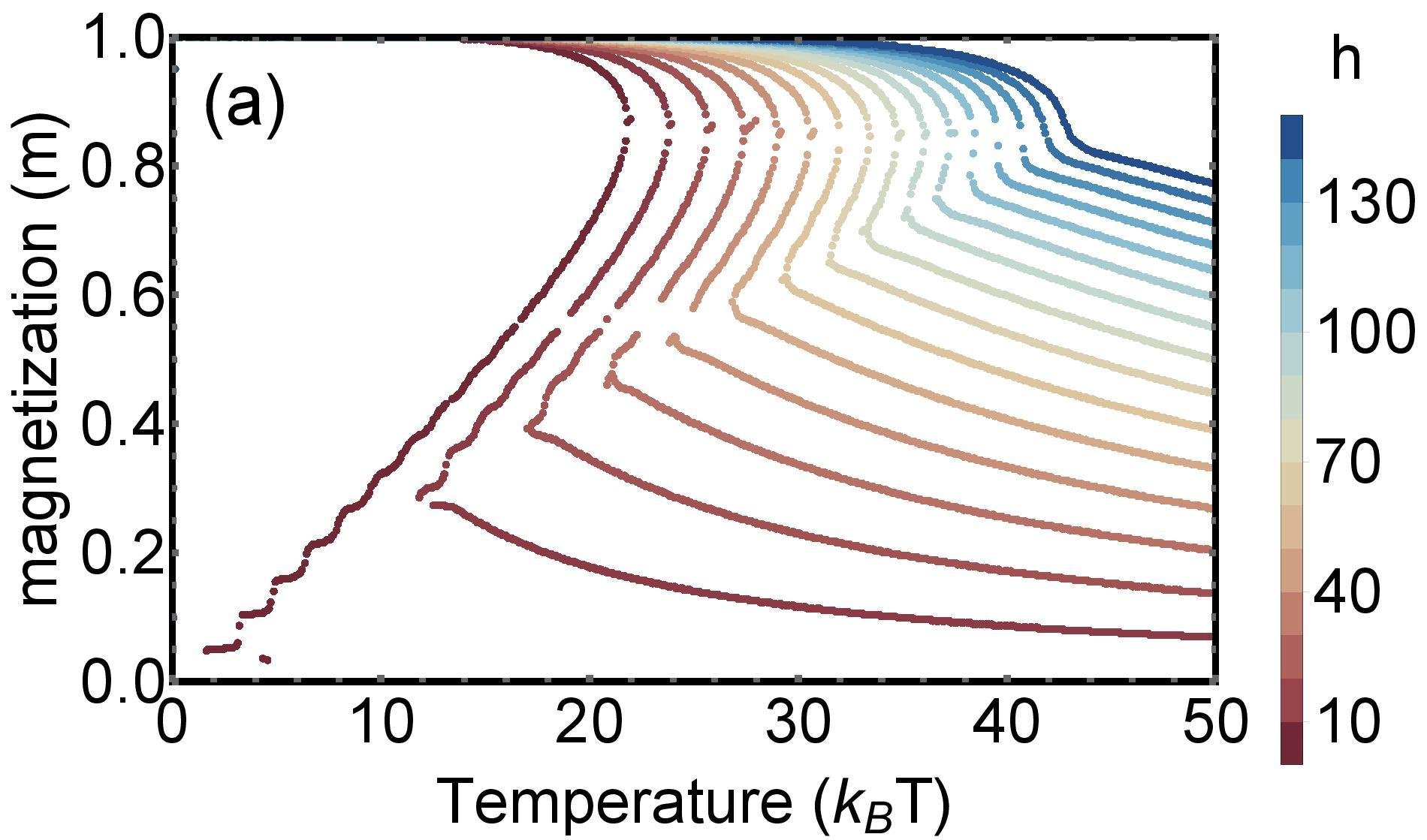

Application online multiplayer game PARDUS


+
=
Science is interdisciplinary.
Thank you
Homophily-Based Social Group Formation in a Spin Glass Self-Assembly Framework
By Jan Korbel
Homophily-Based Social Group Formation in a Spin Glass Self-Assembly Framework
- 288



