Foundations of Entropy I

Why Entropy?

Lecture series at the 

School on Information, Noise, and Physics of Life

Nis 19.-30. September 2022

by Jan Korbel

all slides can be found at: slides.com/jankorbel

Warning!

(Korbel = Tankard = Bierkrug)

No questions are stupid 

Please ask anytime!

Activity I

You have 3 minutes to write down on a piece of paper:

             a) Your name

             b) What do you study

             c) What is entropy to you? (Formula/Concept/Definition/...)

\( S = k \cdot \log W\)

My take on what is entropy

Located at Vienna central cemetery

(Wien Zentralfriedhof)

We will get back to this formula

Why so many definions?

There is more than one face of entropy!

What measures entropy?

Randomness?

Disorder?

Energy dispersion?

Maximum data compression?

'Distance' from equilibrium?

Uncertainty?

Heat over temperature?

Information content?

 Part of the internal energy unavailable for useful work?

Or is it just a tool? (Entropy = thermodynamic action?)

MaxEnt

MaxCal

SoftMax

MaxEP

Prigogine

My courses on entropy

a.k.a. evolution of how powerful entropy is

Field: mathematical physics

warning: Personal opinion!

SS 1st year Bc. - Thermodynamics

 \(\mathrm{d} S = \frac{\delta Q}{T} \)

 \(C_v = T \left( \frac{\partial S}{\partial T}\right)_V\)

 \(\left ( \frac{\partial S}{\partial V}\right)_T = \left(\frac{\partial p}{\partial T} \right)_V \)

SS 2nd year Bc. - Statistical physics

\( S = - \sum_k p_k \log p_k\)

\(Z = \sum_k e^{-\beta \epsilon_k}\)

\(\ln Z = S - U/T\)

SS 3rd year Bc. Quantum mechanics 2

\( S = -Tr (\rho \log \rho) \)

\( Z = Tr (\exp(-\beta \hat{H}))\)

Bachelor's studies

differential forms?

probability theory?

Master's studies

Erasmus exchange 

@ FU Berlin

WS - 2nd year MS - Advanced StatPhys

Fermi-Dirac & Bose-Einstein statistics

Ising spin model and transfer matrix theory

Real gas and virial expansion

WS - 2nd year MS - Noneq. StatPhys

Onsager relations

Molecular motors

Fluctuation theorems

Historical intermezzo

by

Motivations for introducing entropy

1. relation between energy, heat, work and temperature

Thermodynamics (should be rather thermoSTATICS)

2. relation between microscopic and macroscopic

R. Clausius

Lord Kelvin

H. von Helmholtz

S. Carnot

J. C. Maxwell

L. Boltzmann

M. Planck

J. W. Gibbs

Statistical mechanics/physics

Why statistical physics?

Microscopic to Macroscopic

Statistical Physics = Physics + Statistics

Role of statistics in physics

Classical mechanics (quantum mechanics)

- position & momenta given by equations of motion

- 1 body problem: solvable

- 2 body problem: center of mass transform

- 3 body problem: generally not solvable

...

- N body problem: ???

Do we need to know trajectories of all particles?

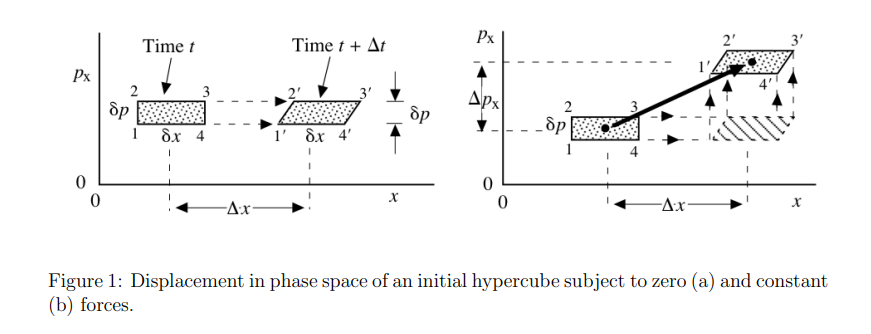
Liouville theorem

Let's have canonical coordinates \(\mathbf{q}(t)\), \(\mathbf{p}(t)\) evolving by Hamiltonian dynamics

$$\dot{\mathbf{q}} =  \frac{\partial H}{\partial \mathbf{p}}\qquad \dot{\mathbf{p}} = - \frac{\partial H}{\partial \mathbf{q}}$$

Let \(\rho(p,q,t)\) be a probability distribution in the phase space. Then, \(\frac{\mathrm{d} \rho}{\mathrm{d} t} = 0.\)

Consequence: \( \frac{\mathrm{d} S(\rho)}{\mathrm{d} t}= - \frac{\mathrm{d}}{\mathrm{d} t} \left(\int \rho(t) \ln \rho(t)\right) = 0.\)

Useful results from statistics

1. Law of large numbers (LLN)

\( \sum_{i=1}^n X_i \rightarrow n \bar{X} \quad \mathrm{for} \ N \gg 1\)

2. Central limit theorem (CLT)

\( (\frac{1}{n} \sum_{i=1}^n X_i - \bar{X}) \rightarrow \frac{1}{\sqrt{n}} \mathcal{N}(0,\sigma^2)\)

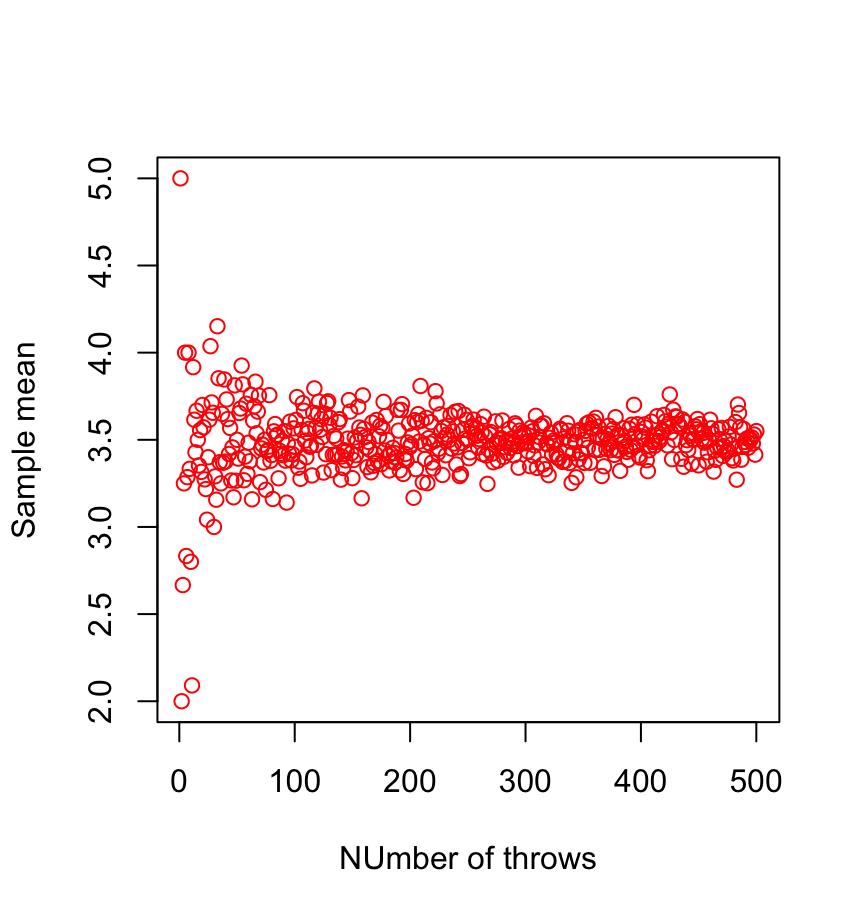
Consequence: a large number of i.i.d. subsystems can be described by very few parameters for \(N \gg 1\)

\(\Rightarrow\) e.g., a box with 1 mol of gas particles

Useful results from combinatorics

Bars & Stars theorems (|*)

Emergence of statistical physics:

Coarse-graining

\(\bar{X}\)

Coarse-graining or Ignorance?

Microscopic systems

Classical mechanics (QM,...)

Mesoscopic systems

Stochastic thermodynamics

Macroscopic systems

Thermodynamics

Coarse-graining in thermodynamics

Microstates, Mesostates and Macrostate

Consider again a dice with 6 states

Let us throw a dice 5 times. The resulting sequence is

Microstate

The histogram of this sequence is

0

0

2

1

1

1

Mesostate

The average value is 3,8    Macrostate

# micro: \(6^5 =7776\)

# meso: \(\binom{6+5-1}{5} =252\)

# macro: \( 5\cdot 6-5\cdot 1 =25\)

Multiplicity W (sometimes \(\Omega\)):

# of microstates with the same mesostate/macrostate

Now we come back to the formula on Boltzmann's grave

Question: how do we calculate multiplicity W for mesostate

Answer: see combinatorics lecture.

Full answer: 1.) permute all states, 2.) take care of overcounting

1.) Permuation of all states: 5! = 120

2.) Overcounting - permutation of                                      2! = 2

Together: \(W(0,2,0,1,1,1) = \frac{5!}{2!} =60\)

0

0

2

1

1

1

"General" formula - multinomials

$$W(n_1,\dots,n_k) = \left(\frac{\sum_{i=1}^k n_i}{n_1, \ \dots \ ,n_k}\right) = \frac{(\sum_{i=1}^k n_k)!}{\prod_{i=1}^k n_i!}$$

The question at stake: WHY \(\log \)?

Succint reason: \(\log\) transforms \(\prod\) to \(\sum\)

(similar to log-likelihood funciton)

Physical reason: multiplicity of \(X \times Y\)

is \(W(X)W(Y)\)

(extensivity/intensivity of thermodynamic variables)

Boltzmann entropy = Gibbs entropy?

\(\log W(n_1,\dots,n_k) = n \log n - \cancel{n} -  \sum_{i=1}^k n_i \log n_i + \cancel{\sum_{i=1}^k n_i} \)

\(= \sum_{i=1}^k n_i (\log n - \log n_i)  = - \sum_{i=1}^k n_i \log \frac{n_i}{n}\)

Stirling's approximation: \( \log(n!) \approx n \log n - n + \mathcal{O}(\log n) \)

Denote: \(\sum_{i=1}^k n_k = n\).

Denote: \(n_i/n = p_i\).

$$\log W(n_1,\dots,n_k) = -  n \sum_{i=1}^k p_i \log p_i $$

What is actually \(p_i\)?

Frequentist vs Bayesian probability

In probability, there are two interpretations of probability

1. Frequentist approach

probability is the limiting success value of a repeated experiment

$$p = \lim_{n \rightarrow \infty} \frac{k(n)}{n}$$

It can be estimated as \(\hat{p} = \frac{X_1+\dots+X_n}{n}\) and it does not  make any sense to consider parametric distribution.

2. Bayesian approach

probability quantifies our uncertainty about the experiment. By observing the experiment we can update our knowledge about it

$$\underbrace{f(p|\hat{p})}_{posterior} = \underbrace{\frac{f(\hat{p}|p)}{f(\hat{p})}}_{likelihood \ ratio} \underbrace{f(p)}_{prior} $$

LLN

Thermodynamic limit

By using the relation \(n_i/n = p_i\), we actually used the frequentist definition of probability. As a consequence, it means that \(n \rightarrow \infty\) (in practical situations \(n \gg 1\)). This limit is in physics called thermodynamic limit.

There are a few natural questions:

Does it mean that the entropy can be used only in the thermodynamic limit?

Does the entropy measure the uncertainty of a single particle in a large system or some kind of average probability over many particles?

(LLN & CLT)

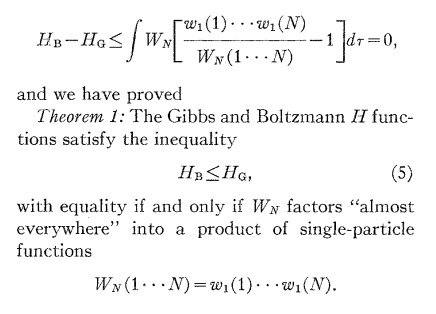
N.B.: does anybody recognize what is \(H_G - H_B\)?

Resolution: what are the states?

Do we consider states of a single dice?

Do we consider states of a pair of dices?

etc.

Do we consider states of an n-tuple of dices?

 ...

Excercise activity for you: can you derive Gibbs entropy from considering the state space of n-tuples of dices?

Two related issues

1. Gibbs paradox 

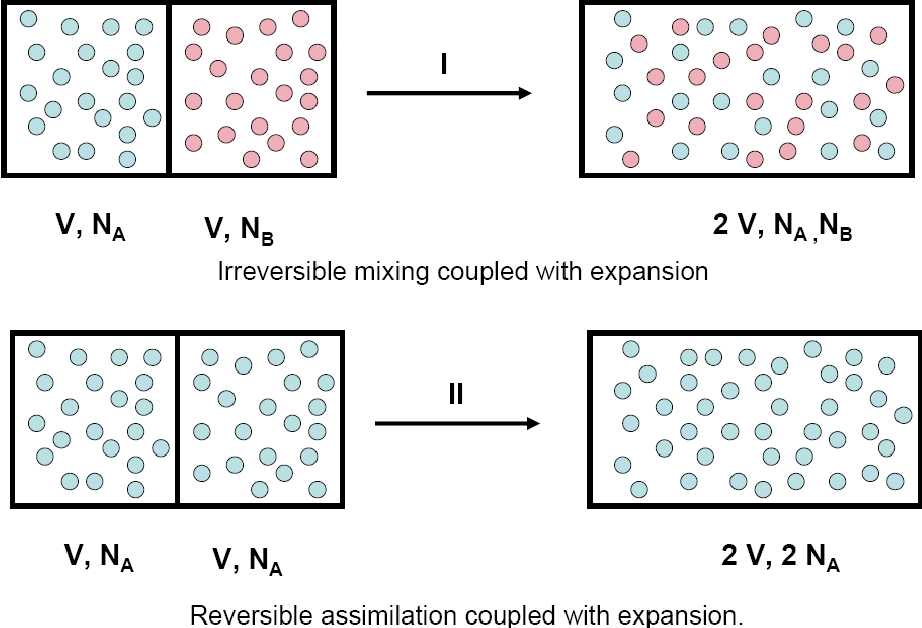
\(\Delta S = k N\ln 2\)

Resolution

1. Simply multiply entropy by 

\(1/N!\) - due to "quantum" reasons (indistinguishability)

2. Swendsen approach

Two related issues

2. Additivity and Extensivity 

(we will come back to it later)

Additivity: We have two independent systems \(A\) and \(B\) $$S(A,B) = S(A) + S(B)$$

Extensivity: We have a system of N particles, then

$$S(kN) = k \cdot S(N)$$

Summary