Thermodynamics
of structure-forming systems
in collaboration with
Simon D. Lindner Rudolf Hanel Stefan Thurner
based on a recently published paper: Nat. Comm. 12 (2021) 1127
Slides available at: https://slides.com/jankorbel



-
Historical review of thermodynamics
-
Main results of stochastic thermodynamics
-
Thermodynamics of structure-forming systems
Outline
Thermodynamics
Microscopic systems
Classical mechanics (QM,...)
Mesoscopic systems
Stochastic thermodynamics
Macroscopic systems
Thermodynamics
Trajectory TD
Ensemble TD
Stochastic Thermodynamics is a thermodynamic theory
for mesoscopic, non-equilibrium physical systems
interacting with equilibrium thermal (and/or chemical)
reservoirs
Statistical mechanics
Historical review of thermodynamics
History
Equilibrium thermodynamics (19 th century)
- Maxwell, Boltzman, Planck, Claussius, Gibbs...
- Macroscopic systems (\(N \rightarrow \infty\)) in equilibrium (no time dependence of measurable quantities - thermoSTATICS)
- General structure of thermodynamics
- Laws of thermodynamics (general)
- Response coefficients (system-specific)
- Applications: engines, refridgerators, air-condition,...


efficiency \(\leq 1-\frac{T_2}{T_1}\)
Heat engine: Carnot cycle

History
Laws of thermodynamics
Zeroth law:
Temperature can be measured. $$T_A = T_B \quad \mathrm{if} \quad A \ \mathrm{and} \ B \ \mathrm{are} \ \mathrm{in} \ \mathrm{equilibrium}.$$
First law (Claussius 1850, Helmholtz 1847):
Energy is conserved.
$${\color{aqua} d}U = {\color{orange} \delta} Q - {\color{orange} \delta} W$$ Second law (Carnot 1824, Claussius 1854, Kelvin):
Heat cannot be fully transformed into work. $${ \color{aqua} d} S \geq \frac{{\color{orange} \delta} Q}{T}$$ Third law: We cannot bring the system into the absolute zero
temperature in a finite number of steps. $$ \lim_{T \rightarrow 0} S(T) = 0$$
History
Local equilibrium thermodynamics (1st half of 20th cent.)
- Onsager, Rayleigh...
- Systems close to equilibrium - linear response theory
- Local equilibrium: subsystems a,b,c are each in equilibrium

Total entropy \(S \approx S^a + S^b + S^c + \dots\)
Entropy production \(\sigma^a = \frac{d S^a}{d t} = \sum_i Y_i^a J_i^a \)
\(Y_i^a\) - thermodynamic forces; \(J_i^a\) - thermodynamic currents
4th Law of thermodynamics (Onsager 1931): \( \sigma = \sum_{ij} L_{ij} \Gamma_i \Gamma_j\)
\(\Gamma_i = Y_i^a - Y_i^b \) - afinity, \(L_{ij}\) - symmetric
History and now
Stochastic thermodynamics (90s of 20th century - present)
- Evans, Jarzynski, Crooks, Seifert, van den Broek,....
- Mesoscopic systems far from equilibrium
- Combines stochastic calculus and non-equilibrium thermodynamics
- Main results: Trajectory thermodynamics, Fluctuation theorems, Thermodynamic uncertainty relations, Speed limit theorems,...
- Applications: colloidal particles and soft matter, biochemistry, molecular motors
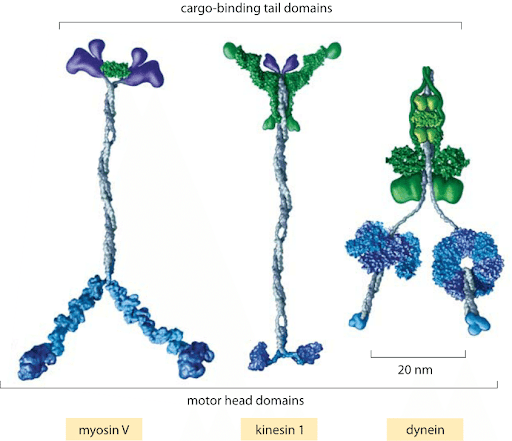
Molecular motor: myosin walking on actin filament
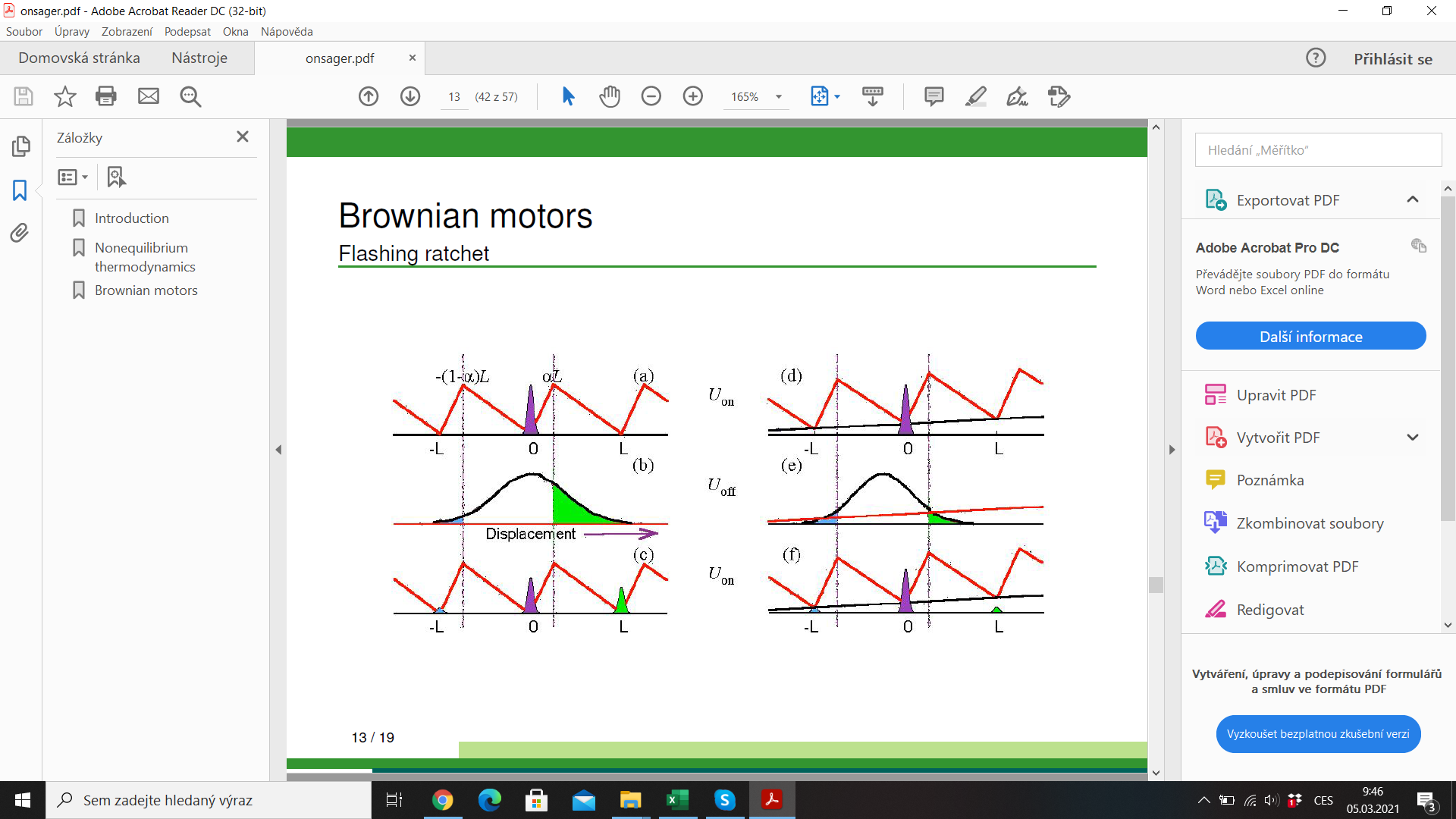
efficiency \(\lesssim 1\)
Main results of stochastic thermodynamics
Stochastic thermodynamics
1.) Consider linear Markov (= memoryless) with distribution \(p_i(t)\).
Its evolution is described by master equation
$$ \dot{p}_i(t) = \sum_{j} [w_{ij} p_{j}(t) - w_{ji} p_i(t) ]$$
\(w_{ij}\) is transition rate.
2.) Entropy of the system - Shannon entropy \(S(P) = - \sum_i p_i \log p_i\). Equilibrium distribution is obtained by maximization of \(S(P)\) under the constraint of average energy \( U(P) = \sum_i p_i \epsilon_i \)
$$ p_i^{eq} = \frac{1}{Z} \exp(- \beta \epsilon_i) \quad \mathrm{where} \ \beta=\frac{1}{k_B T}, Z = \sum_j \exp(-\beta \epsilon_j)$$
Stochastic thermodynamics
3.) Detailed balance - stationary state (\(\dot{p}_i = 0\) ) coincides with the equilibrium state (\(p_i^{eq}\)). We obtain
$$\frac{w_{ij}}{w_{ji}} = \frac{p_i^{eq}}{p_j^{eq}} = e^{\beta(\epsilon_j - \epsilon_i)}$$
4.) Second law of thermodynamics:
$$\dot{S} = - \sum_i \dot{p}_i \log p_i = \frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{p_j}{p_i}$$
$$ =\underbrace{\frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{w_{ij} p_j}{w_{ji} p_i}}_{\dot{S}_i} + \underbrace{\frac{1}{2} \sum_{ij} (w_{ij} p_j - w_{ji} p_i) \log \frac{w_{ji}}{w_{ij}}}_{\dot{S}_e}$$
\( \dot{S}_i \geq 0 \) - entropy production rate (2nd law of TD)
\(\dot{S}_e = \beta \dot{Q}\) entropy flow rate
Stochastic thermodynamics
5.) Trajectory thermodynamics - consider stochastic trajectory
\(x(t)= (x_0,t_0;x_1,t_1;\dots)\). Energy \(E_x = E_x(\lambda(t))\), \(\lambda(t)\) - control protocol
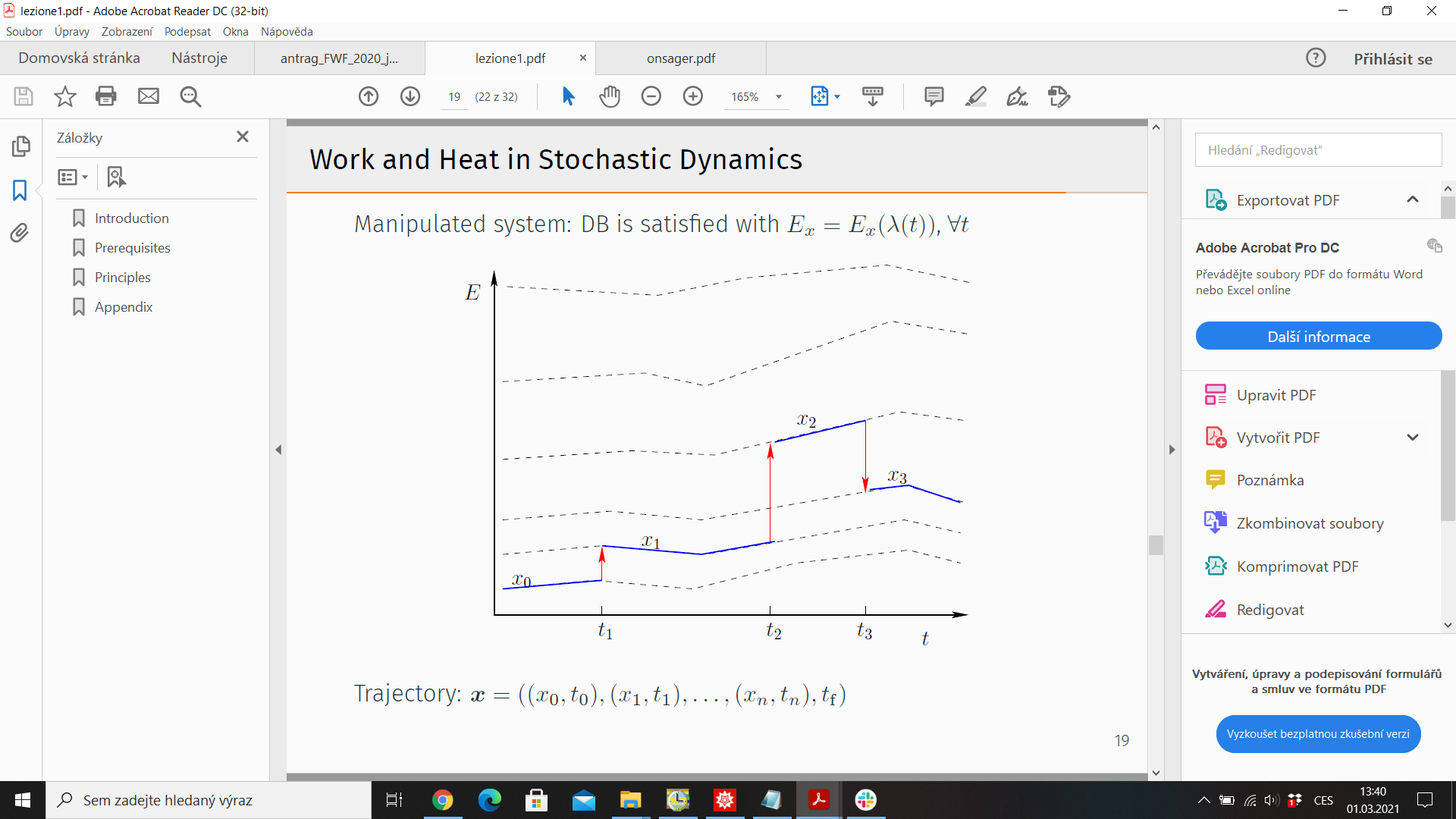
Probability of observing \( x(t)\): \(\mathcal{P}(x(t)\))
Time reversal \(\tilde{x}(t) = x(T-t)\)
Reversed protocol \(\tilde{\lambda}(t) = \lambda(T-t)\)
Probability of observing reversed trajectory under reversed protocol \(\tilde{\mathcal{P}}(\tilde{x}(t))\)
Stochastic thermodynamics
6.) Fluctuation theorems
Trajectory entropy: \(s(t) = - \log p_x(t)\)
Trajectory 2nd law \(\Delta s = \Delta s_i + \Delta s_e\)
Relation to the trajectory probabilities
$$\log \frac{\mathcal{P}(x(t))}{\tilde{\mathcal{P}}(\tilde{x}(t))} = \Delta s_i$$
Detailed fluctuation theorem
$$\frac{P(\Delta s_i)}{\tilde{P}(-\Delta s_i)} = e^{\Delta s_i}$$
Integrated fluctuation theorem $$ \langle e^{- \Delta s_i} \rangle = 1 \quad \Rightarrow \langle \Delta s_i \rangle = \Delta S_i \geq 0$$
Thermodynamics of structure-forming systems
Motivation
- Many systems form structures: molecules of atoms, clusters of colloidal particles, (bio)polymers or micelles
- We study the thermodynamics of structure-forming systems
- For small systems, we get a correction to Shannon entropy
- We apply the results to several physical systems
- We derive fluctuation theorems for structure-forming systems
Toy model - magnetic coin model
We consider a coin with two states: head and tail
The coins are magnetic and can stick together
How many states we get for N coins?
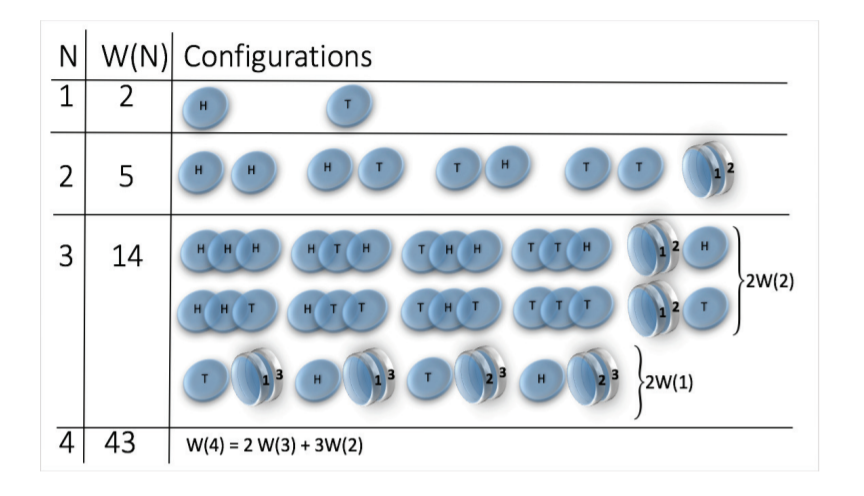
\(W(N) \sim N^N\)
(non-magnetic coins \(W(N) = 2^N\))



picture taken from: H. J. Jensen et al 2018 J. Phys. A: Math. Theor. 51 375002
Multiplicity and entropy
of structure-forming systems
Boltzmann entropy formula: \(S(n_i) = k_B \log W(n_i)\)
where \(W\) is multiplicity
(number of microstates corresponding to a mesostate \(n_i\))
Microstate: state of each particle
if more particles are bound to a molecule, then state of each molecule
Mesostate: how many particles and/or molecules are in given state
Example: magnetic coin model: 3 coins, magnetic
microstates mesostate multiplicity


2 x 1x
1 x 1x
3
3




How to calculate a multiplicity?
- Consider a mesostate
- Make all permutations of particles
- Some microstates are overrepresented - calculate how many permutations belong to the same microstate
Examples
2 x 1x
1 x 1x










1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1
1 1 2 2 3 3
2 3 1 3 1 2
3 2 3 1 2 1



= (1,2,3) , (2,1,3)
= (1,3,2) , (3,1,2)
= (2,3,1) , (3,2,1)



= (1,2,3) , (1,3,2)
= (2,1,3) , (2,3,1)
= (3,1,2) , (3,2,1)
General formula for multiplicity
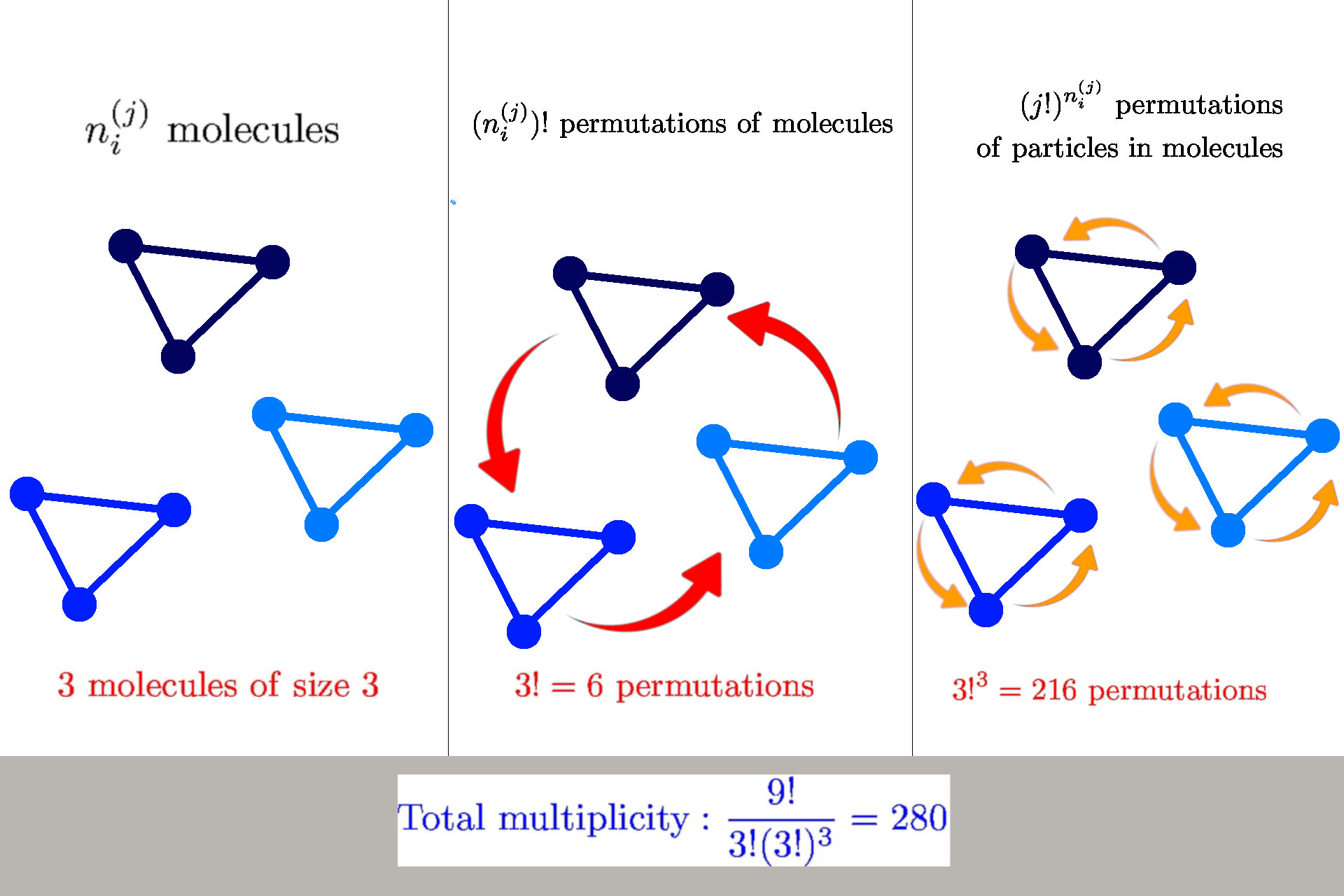
General formula: \(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}! {\color{aqua} (j!)^{n_i^{(j)}}}}\)
we have \(n_i^{(j)}\) molecules of size \(j\) in a state \(s_i^{(j)}\)

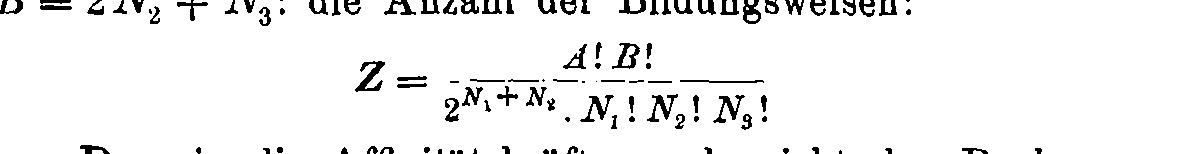
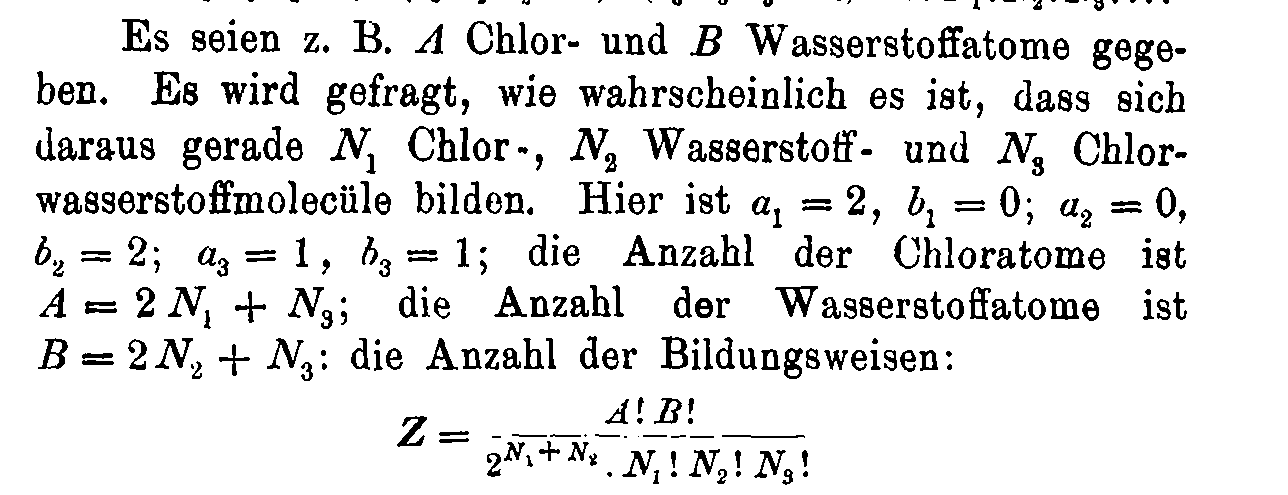
Boltzmann's 1884 paper
Entropy of structure-forming systems
$$ S = \log W \approx n \log n - \sum_{ij} \left(n_i^{(j)} \log n_i^{(j)} - n_i^{(j)} + {\color{aqua} n_i^{(j)} \log j!}\right)$$
Introduce "probabilities" \(\wp_i^{(j)} = n_i^{(j)}/n\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{aqua}- 1}) {\color{aqua}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{n^{j-1}}}$$
Finite interaction range: concentration \(c = n/b\)
$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{aqua}- 1}) {\color{aqua}- \sum_{ij} \wp_i^{(j)}\log \frac{j!}{{\color{orange}c^{j-1}}}}$$
Equilibrium distribution:
$$\hat{\wp}_i^{(j)} = \frac{c^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$
normalization by solving
\(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{c^{j-1}}{(j-1)!} e^{-{\color{aqua} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{aqua} \alpha}\)
Entropy of structure-forming systems
Main properties:
- The entropy fulfills Shannon Khinchin axioms 1,3,4 but does not fulfill axiom SK 2 (it is not maximized by uniform distribution)
- The entropy fulfills Lieb-Yngvason axioms (it is additive, and it is extensive for \(c=const\) )
- The entropy fulfills Shore-Johnson axioms 1,3,4 but does not fulfill axioms SJ 2 (permutation/coordinate invariance)
- The entropy fulfills Tempesta group-composability axiom but is not symmetric in its arguments
- The scaling exponents according to Hanel-Thurner axioms are \(c=0,d=1\), the same as for Shannon entropy
\( \Rightarrow\) The entropy satisfies all common axiomatic schemes but it is not symmetric in probabilities
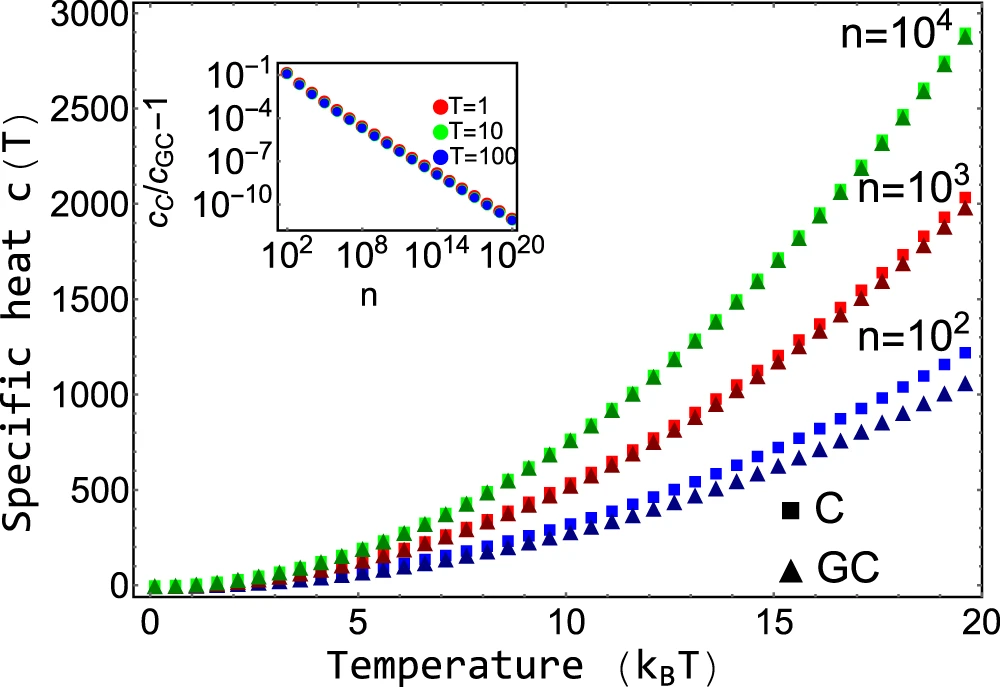
Comparison with Grand-canonical ensemble
Applications
Self-assembly of Janus particles
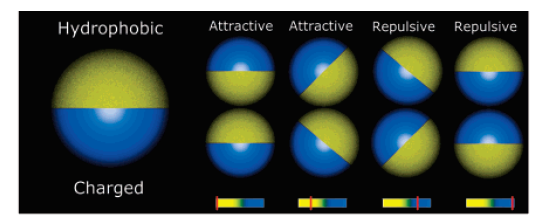
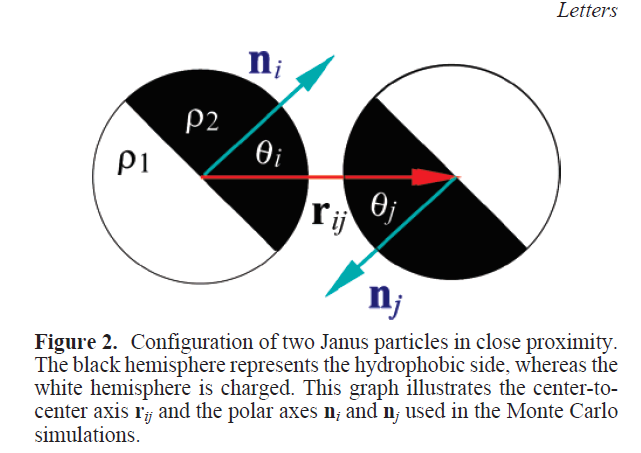

Kern-Frenkel model
Pair-wise potential: \(U^{KF}(r_{ij},n_i,n_j) = u(r_{ij}) \Omega(r_{ij},n_i,n_j) \)
Square-well interaction with hard sphere:
$$ u(r_{ij}) = \left\{ \begin{array}{rl} \infty, & r_{ij} \leq \sigma \\ - \epsilon, & \sigma < r_{ij} < \sigma + \Delta \\ 0, & r_{ij} > \sigma + \Delta. \end{array} \right.$$
\(\Omega\) decribes orientation of particles:
Particle coverage \(\chi = \sin^2(\theta/2) = \frac{1-\cos{\theta}}{2}\)
Polymers: \(\chi = 0.3\)
Janus particles: \(\chi = 0.5\)
Crystalic structures: \(\chi = 0.6\) (stable lamellar crystals)
$$\Omega(r_{ij},n_i,n_j) = \left\{\begin{array}{rl} -1 & \mathrm{if} \ r_{ij} \cdot n_i > \cos(\theta) \ \mathrm{and} \ r_{ij} \cdot n_j > \cos(\theta)\\ 0 & \mathrm{otherwise} \end{array} \right.$$
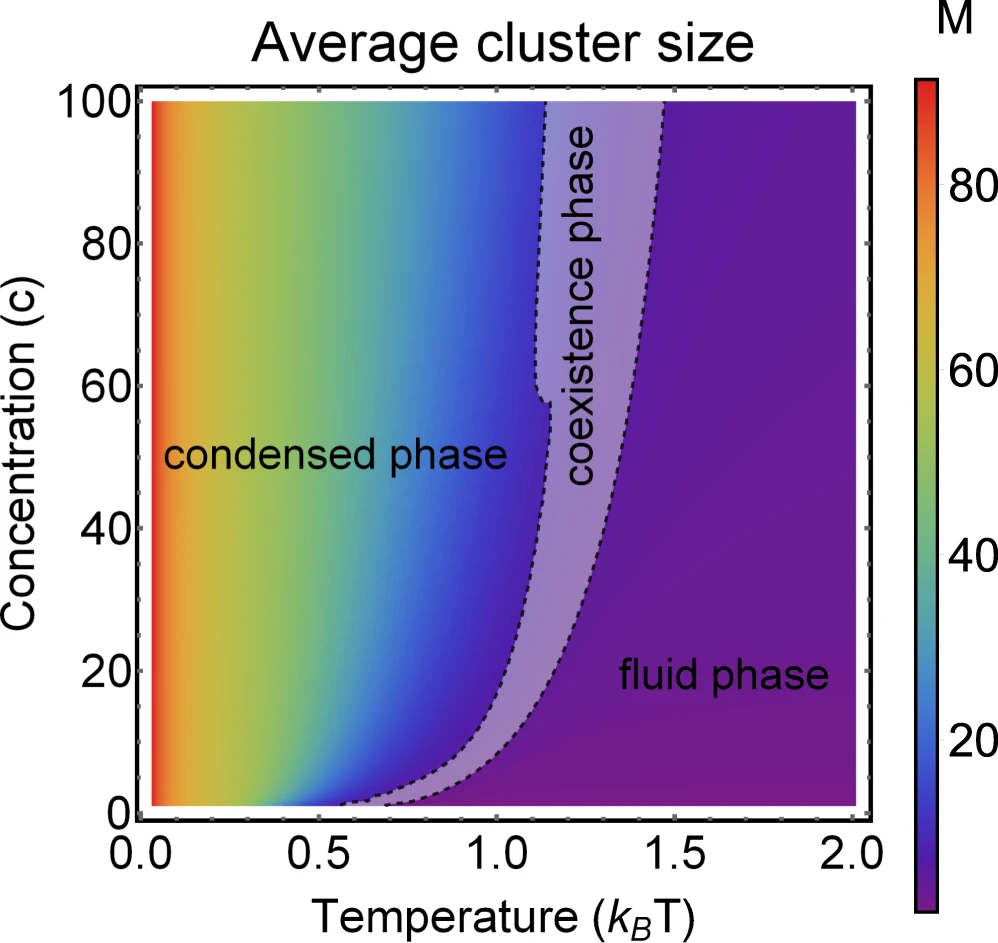
Phase diagram of Janus particles for average cluster size \(M\)
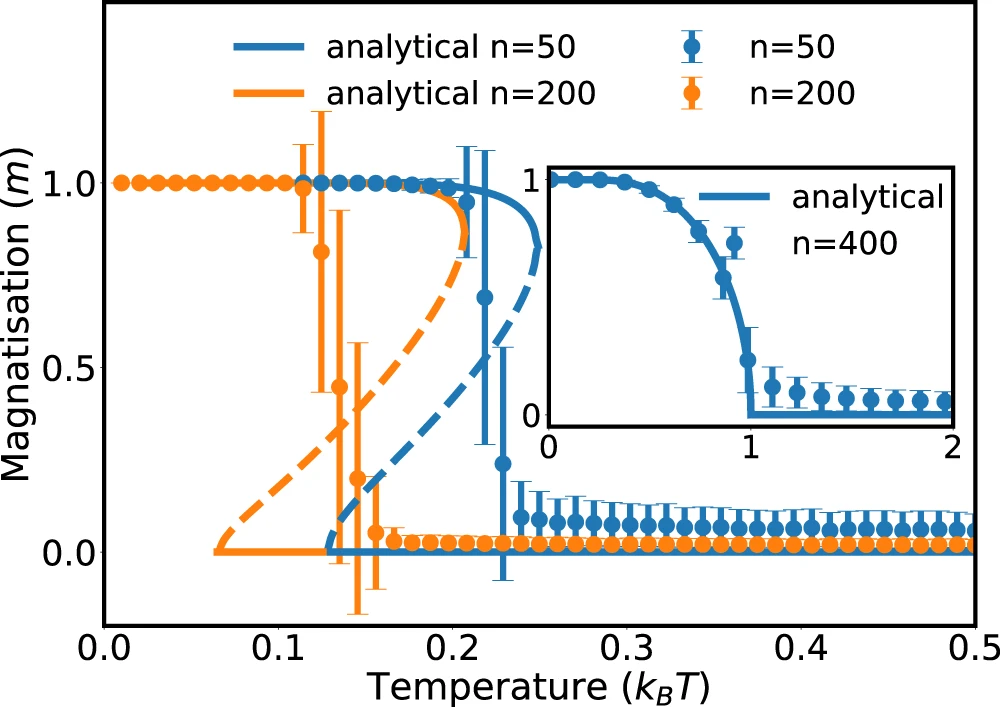
Currie-Weiss model with molecules
(= fully connected Ising model with bound states)
$$ H(\sigma_i) = - \frac{J}{n-1} \sum_{i \neq j, \ free} \sigma_i \sigma_j - h \sum_{j, \ free} \sigma_j $$
Stochastic thermodynamics of structure-forming systems
1. Linear Markov (= memoryless) with distribution \(\wp_i(t)\).
Its evolution is described by master equation
$$ \dot{\wp}_i(t) = \sum_{j} [w_{ij} \wp_{j}(t) - w_{ji} \wp_i(t) ]$$
\(w_{ij}\) is transition rate.
2. Detailed balance
|
$$\frac{{w}_{ik}^{jl}}{{w}_{ki}^{lj}}= \frac{\hat{\wp}_i^{(j)}}{\hat{\wp}_{k}^{(l)}} = {\color{aqua}\frac{j!}{l!}{c}^{l-j}}\exp \left[{\color{aqua}\alpha (l-j)}+\beta \left({\epsilon }_{k}^{(l)}-{\epsilon }_{i}^{(j)}\right)\right]$$ |
Assumptions
Stochastic thermodynamics of structure-forming systems
Results
1. Second law of thermodynamics for non-equilibrium systems
|
$$\frac{{\rm{d}}{\mathcal{S}}}{{\rm{d}}t}={\dot{{\mathcal{S}}}}_{i}+\beta \dot{{\mathcal{Q}}}$$ where \(\dot{\mathcal{S}}_i \geq 0\) is entropy production flow and \(\dot{\mathcal{Q}}\) is the heat flow |
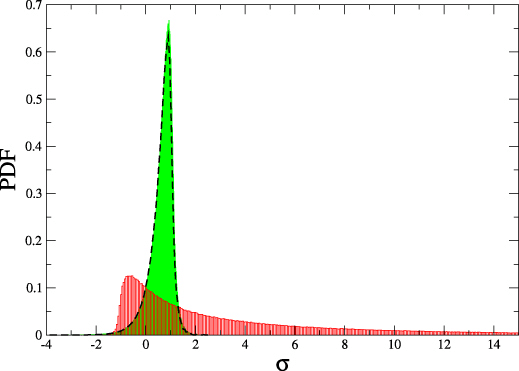
2. Detailed fluctuation theorem for structure forming systems
$$\frac{P(\Delta \sigma)}{\tilde{P}(-\Delta \sigma)} = e^{\Delta \sigma}$$
where \(\Delta \sigma = \Delta s_i + {\color{aqua} \log j_0 - \log j_f}\)
\(\Delta s_i\) is the trajectory entropy production
Summary
More details in: J. Korbel, S. D. Lindner, R. Hanel and S. Thurner,
Nat. Comm. 12 (2021) 1127
- We derived the formula for entropy of structure-forming systems
- For large systems and low concentrations, it is equivalent to the grand-canonical ensemble
- We showed several applications in self-assembly or Currie-Weis model with molecule states
- We derived second law of thermodynamics and detailed fluctuation theorem for structure-forming systems arbitrarily far from equilibrium
Thermodynamics of structure-forming systems
By Jan Korbel
Thermodynamics of structure-forming systems
- 352



