C / C++
Misc & Random
Jason
Table of Content
- Miscellaneous
- Type Casting
- auto Keyword
- Random
- Pseudo-Random Number Generator
- Monte Carlo Method
- Simple XOR Cipher
Miscellaneous - Type Casting
Implicit Type Casting
Explicit Type Casting
int floor(double);
void someFunc(){
float x;
//...
x = floor(x);
//...
}double pi = 3.14159;
cout << "Pi = ";
cout << (int) pi << endl;Implicit Type Casting
編譯器自動幫你進行型態轉換，不用指定型別
Warning: data loss
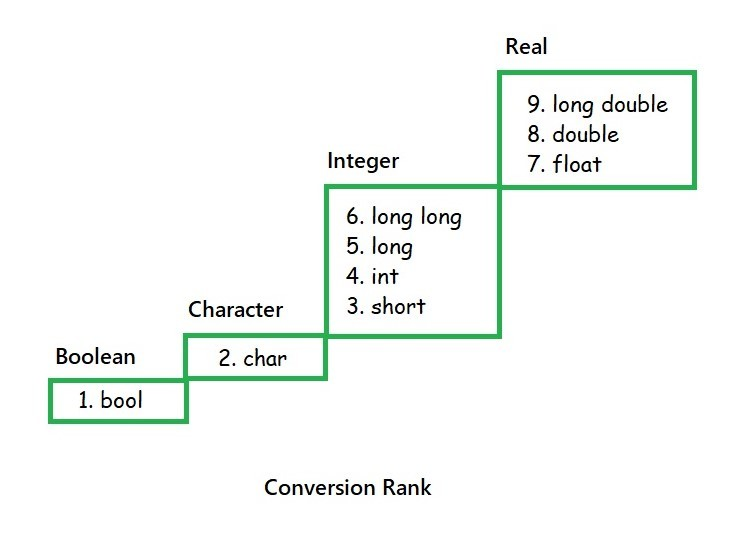
Explicit Type Casting
用 (type) 指定轉換型別
Define your own type casting impl.
#include <iostream>
using namespace std;
struct X {
operator int(){ return 3; }
explicit operator float() {return 4.5;}
};
int main() {
X x;
int k = x;
cout << k << endl;
cout << (float)x << endl;
return 0;
}Miscellaneous - auto Keyword
懶得宣告變數型別？
Compiler can infer the type for you.
auto i = 10;
auto f = 3.14;
auto s = "Hello?";
auto k = s;
/*
auto k; // invalid, the compiler can't infer the type.
*/
vector<int> vec;
for(auto i: vec){
cout << i << endl;
}Random
Do you really understand random?
Pseudo-Random Number
- Generated by "deterministic" algorithm "seeded" with small entropy
- Can be fast generated
Random Number
- Generated by collecting "real" entropy (eg: keypress duration)
- Require real-world input
- Can be slow generating them
It's still open problems to
1) effectively extract entropy from the real-world, and
2) find secure and efficient PRNG algorithms.
In the "Meme"while
LCG - Linear Congruential Generator
A simple, but not secure, example of PRNG
N_{j+1} = (A \times N_j + B) \bmod M
Pros and Cons
- Low computation overhead
- No I/O required, simple idea
- Is not cryptographically-secure
- Attackable... How? M? A? B?
N_{i+1} \equiv_M (A \times N_{i+0} + B)\\
N_{i+2} \equiv_M (A \times N_{i+1} + B)\\
(N_{i+2} - N_{i+1}) \equiv_M A\times (N_{i+1} - N_{i+0})
Implementation?
C / C++ already implemented rand() for you!
int rand() / srand(unsigned seed)
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
int main(){
srand(time(NULL));
// seeding the PRNG with current time
int trial = 1000;
double total = 0.0;
for(int i = 0; i < trial; i++){
int roll = rand() % 6 + 1;
if(roll <= 4)
total -= roll * 1.5;
else
total += roll;
}
total /= trial;
cout << total << endl;
}| Trial | Total / Trial |
|---|---|
| 100 | -0.51 |
| 1000 | -0.5445 |
| 10000 | -0.65995 |
| 100000 | -0.661445 |
| 1000000 | -0.662112 |
Example Usage: Dice Game Simulation
E[X] = \frac{-1.5(1+2+3+4)+5+6}{6} \\
= -\frac{2}{3}
Monte-Carlo Method
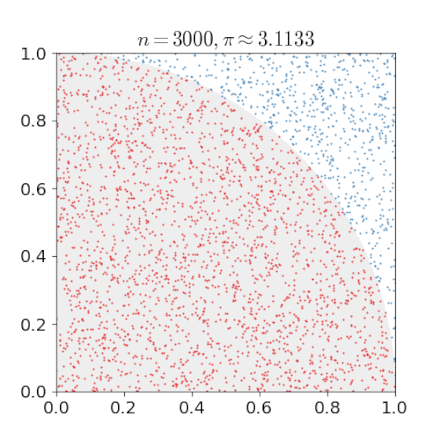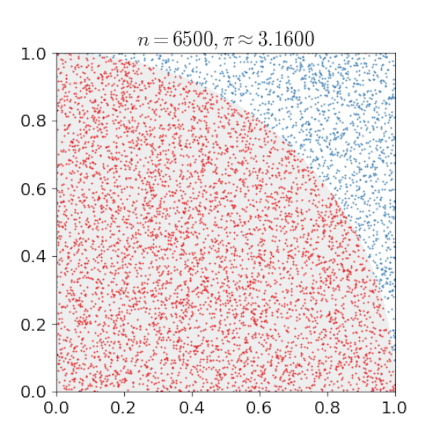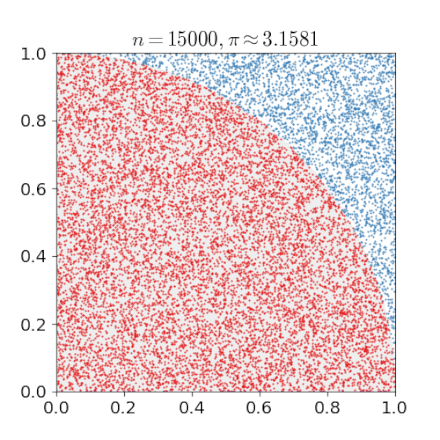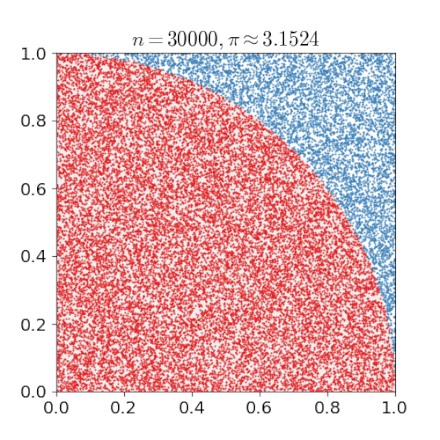
Solving hard problems by "simulation"
- Estimation under complex rules
- Estimating π
Practice time?
#include <iostream>
#include <iomanip>
#include <random>
#include <cmath>
using namespace std;
double monte_carlo(int t){
double c = 0;
for(int i = 0; i < t; i++){
double x = (double)rand() / RAND_MAX;
double y = (double)rand() / RAND_MAX;
if(pow(x, 2) + pow(y, 2) <= 1.0)
c += 1.0;
}
return c / t * 4;
}
double p13(int k){
double res = 1;
for(int i = 1; i <= k; i++){
double l = (2 * i)*(2 * i);
double r = (2 * i - 1) * (2 * i + 1);
res *= l / r;
}
return res * 2;
}
int main(){
int t;
cin >> t;
double m = monte_carlo(10000000);
double p = p13(t);
cout << fixed << setprecision(2) << abs(p - m) << endl;
return 0;
}XOR Cipher
How to encrypt a message?
- XOR Cipher
- 0 ^ 0 = 0
- 0 ^ 1 = 1
- 1 ^ 0 = 0
- 1 ^ 1 = 1
c = m \oplus k
m = c \oplus k = (m\oplus k) \oplus k
Cons: The key must have the same length of the message
What if we generate the key with a shorter passphrase?
XOR Cipher
void encrypt(char message[], int len, int passphrase){
srand(passphrase);
for(int i = 0; i < len; i++)
message[i] ^= rand() % 256;
}
void decrypt(char message[], int len, int passphrase){
/*
???
*/
}Use passphrase as seed to generate the passphrase with PRNG
Homework Time!
Decrypt a encrypted message
Hint: What if we try breaking the message from the seed?
C++
By jason-plainlog
