C++
Misc Advanced (?)
Outline
-
sort & compare
- Merge Sort, std::sort, compare
-
lower_bound
- Binary Search, Count Numbers in Range
-
next_permutation
- N-Queens in O(n!)
- More?
Sort and Compare
We know about bubble sort O(n^2) right now
But sorting can actually be done in O(n log n), how?
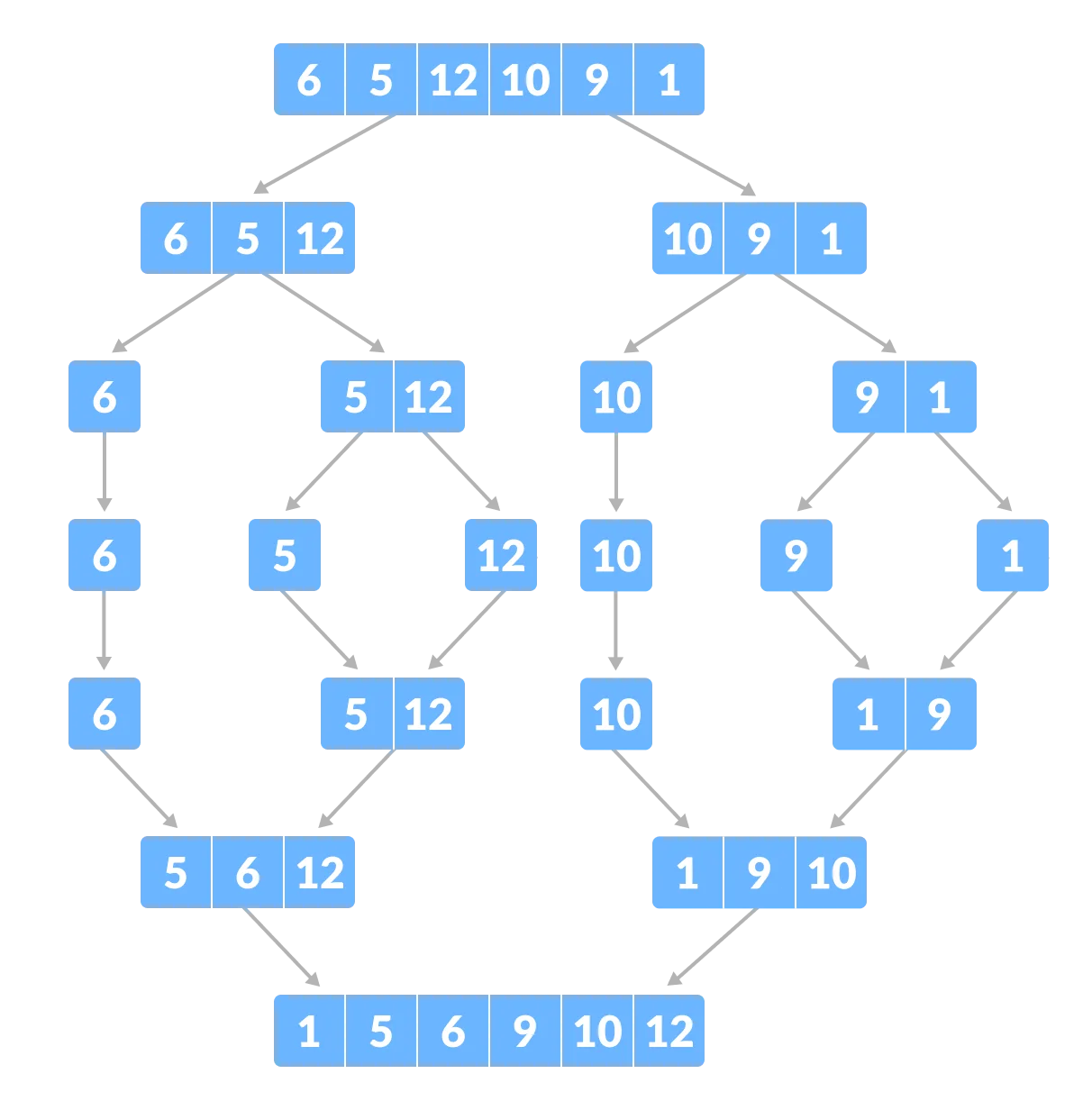
Merge Sort Algorithm
O(nlogn) =
O(n) each layer x O(logn) layers
O(nlogn) Sort
No worries, std lib got you covered!
Just include <algorithm> and use std::sort
p.s. std::sort is actually Quick Sort, but the complexity is similar
#include <algorithm>
#include <iostream>
using namespace std;
int main(){
int n;
cin >> n;
int arr[n];
for(int i = 0; i < n; i++)
cin >> arr[i];
sort(arr+0, arr+n);
for(int i = 0; i < n; i++)
cout << arr[i] << endl;
return 0;
}#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int main(){
int n;
cin >> n;
vector<int> arr(n);
for(int i = 0; i < n; i++)
cin >> arr[i];
sort(arr.begin(), arr.end());
for(int i = 0; i < n; i++)
cout << arr[i] << endl;
return 0;
}std::sort with compare
What if I want to sort custom defined types like structs?
#include <iostream>
#include <algorithm>
using namespace std;
struct point {
int x, y;
};
bool cmp(point &a, point &b){
if(a.x != b.x) return a.x < b.x;
return a.y < b.y;
}
int main() {
point ps[10];
sort(ps, ps+10, cmp);
for(int i = 0; i < 10; i++)
cout << "(" << ps[i].x << ", " << ps[i].y << ")" << endl;
return 0;
}You can specify a compare function to std::sort
Binary Search
A technique taking advantage of "sorted" property
If given a 1024-page book, ask you to open the 528th page.
What's the fastest way to do it?
(Assuming open each page takes the same time)
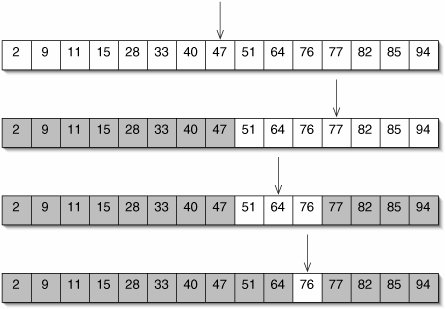
Time Complexity?
O(logN)
O(NlogN) sort once
get you O(logN) search!
Binary Search


No worries, again!
std library also got you covered!
You can use lower_bound to do binary search
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int arr[10] = {2,6,3,4,6,8,1,2,3,4};
sort(arr, arr+10);
for(int i = 0; i < 10; i++)
cout << arr[i] << " ";
cout << endl;
// 1, 2, 2, 3, 3, 4, 4, 6, 6, 8
cout << *lower_bound(arr, arr+10, 6) << endl; // 6
cout << lower_bound(arr, arr+10, 6) - arr << endl; // 7
return 0;
}The lower_bound function finds the first value >= target value
Noted that lower_bound returns a pointer-like type
Example: Count Numbers in Range
Given an array of numbers Xi and several ranges (a, b),
can you count how many numbers within [a, b] for each range?
eg: X = [2,3,5,7,11,13,15], (a, b) = (6, 13)
output: 3 (7, 11, 13)
Most naive solution:
O(NQ), where Q is # of queries
Sort then binary search:
O(NlogN + QlogN) = O((N + Q)logN)
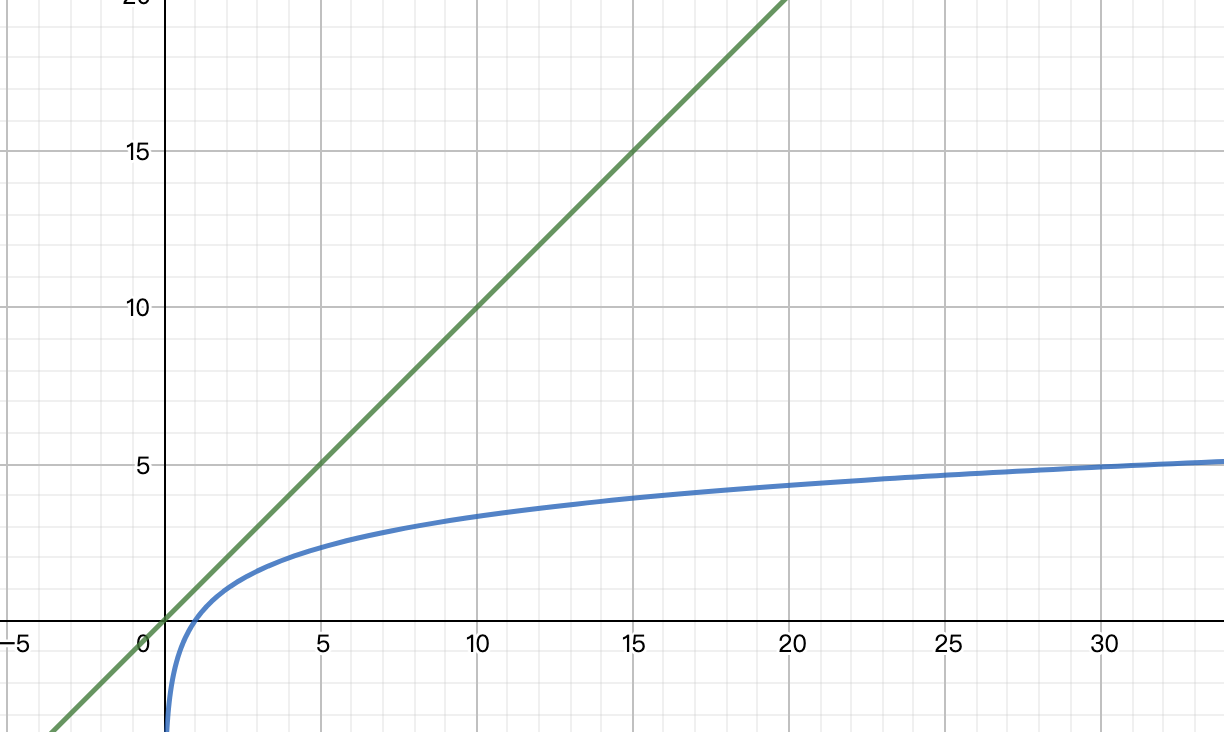
This is a logarithmic boost in time complexity!
Example: Count Numbers in Range
Given an array of numbers Xi and several ranges (a, b),
can you count how many numbers within [a, b] for each range?
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int n, q;
cin >> n >> q;
vector<int> v(n);
for(int i = 0; i < n; i++) cin >> v[i];
sort(v.begin(), v.end());
int l, r;
while(q-- && cin >> l >> r)
cout << lower_bound(v.begin(),v.end(),r) - lower_bound(v.begin(),v.end(),l) + 1 << endl;
return 0;
}Next Permutation
A technique taking advantage of "sorted" property
If given a 1024-page book, ask you to open the 528th page.
What's the fastest way to do it?
(Assuming open each page takes the same time)

Time Complexity?
O(logN)
O(NlogN) sort once
get you O(logN) search!
N-Queens Problem
Place N queens on NxN board
and only one in each row/column/diagonal

Naive Solution?
O(2^(N^2)*N^2)?
N-Queens Problem
Each row can only have one,
how about checking permutations of [0,1,2,3,4,5,6,7]?

O(n!*n^2)
next_permutation
#include <iostream>
using namespace std;
int main(){
int n;
cin >> n;
vector<int> arr(n);
for(int i = 0; i < n; i++)
arr[i] = i;
do {
if(legal(arr)) break;
} while(next_permutation(arr.begin(), arr.end()));
output(arr);
return 0;
}The arr should be sorted in the begining!
More?
竹區的講師幫大家收集了很多實用 functions
歡迎自己研究 XD
C++ Misc Advanced
By jason-plainlog
C++ Misc Advanced
- 388



