Foundations of Interpretable AI
Tutorial @
PART I: Motivation and Post-hoc Methods
(8:00 - 9:00 am)
Aditya Chattopadhyay (Amazon)
PART II: Shapley Value based Methods
(9:15 - 10:15 am)
Jeremias Sulam (Johns Hopkins)
PART III: Interpretable by Design Methods
(10:30 - 11:30 am)
René Vidal (Penn)
Coffee break
(10:15- 10:30 am)
Coffee break
(9:00- 9:15 am)
Shapley Values
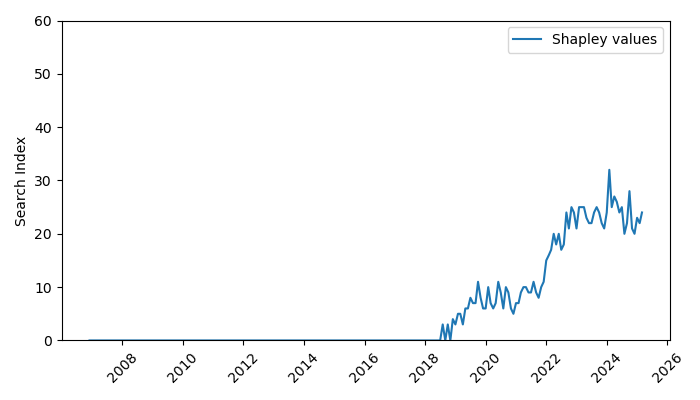
Popularity on
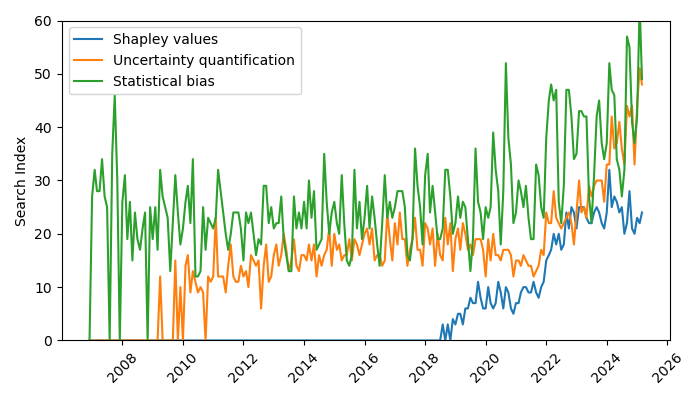
Popularity on
Shapley Values
TODAY
What are they?
How are they computed?
(Shapley for local feature importance)
- Not an exhaustive literature review
- Not a code & repos review
- Not a demonstration on practical problems
- Review of general approaches and methodology
- Pointers to where to start looking in different problem domains
Shapley Values
Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
Let be an -person cooperative game with characteristic function
G = ([n],v)
n
v : \mathcal P([n]) \mapsto \mathbb R
How important is each player for the outcome of the game?
Shapley Values
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
marginal contribution of player i with coalition S
Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
Shapley Values
-
Efficiency
\displaystyle v([n]) = v(\empty) + \sum_{i=1}^n \phi_i(v)
-
Linearity
\displaystyle \phi_i( \alpha_1 v_1 + \alpha_2 v_2) = \alpha_1 \phi_i(v_1) + \alpha_2 \phi_i(v_2) \newline \text{ for characteristic functions }v_1,v_2
-
Symmetry
\text{If}~~ v(S\cup i) = v(S\cup j) ~~ \forall S\subseteq [n]\setminus \{i,j\} \newline \text{Then}~~ \phi_i(v) = \phi_j(v)
\text{If}~~ v(S\cup i) = v(S) ~~ \forall S\subseteq [n]\setminus \{i\} \newline \text{Then}~~ \phi_i(v)=0
-
Nullity
Shapley Explanations for ML
lung opacity
cardiomegaly
fracture
no findding
X \in \mathcal X \subset \mathbb R^n
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
f(X) = \hat{Y} \approx Y
Y\in \mathcal Y = [C]
Shapley Explanations for ML
Question 2:
How can we (when) compute \(\phi_i(v)\)?
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Question 1:
How should (can) we choose the function \(v\)?
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } \frac{|S|!(n-|S|-1)!}{n!} \left[ v(S\cup \{i\}) - v(S) \right]
X \in \mathcal X \subset \mathbb R^n
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
f(X) = \hat{Y} \approx Y
Y\in \mathcal Y = [C]
Shapley Explanations for ML
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:
How can we (when) compute \(\phi_i(v)\)?
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Question 1:
How should (can) we choose the function \(v\)?
X \in \mathcal X \subset \mathbb R^n
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
f(X) = \hat{Y} \approx Y
Y\in \mathcal Y = [C]
Question 1:
How should (can) we choose the function \(v\)?
For any \(S \subseteq [n]\), and a sample \(x\sim p_X\), we need
\(v_f(S,x) : \mathcal P([n])\times \mathcal X \to \mathbb R\)
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]
Question 1:
How should (can) we choose the function \(v\)?
- Fixed reference value
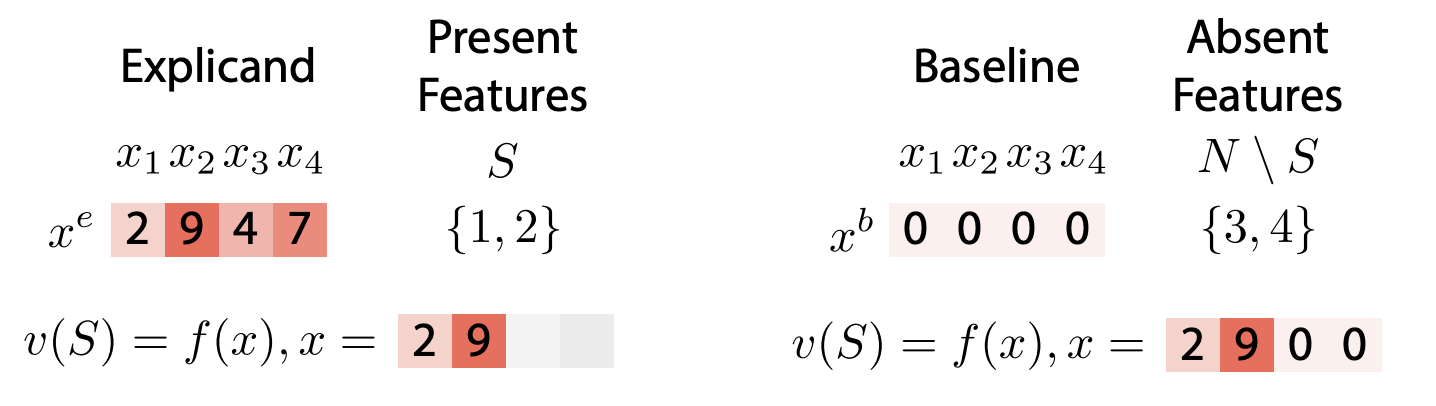
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]
\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ f(x_{S\cup i},x^b_{\overline{S\cup i}}) - f(x_{S},x^b_{\overline{S}}) \right]
Question 1:
How should (can) we choose the function \(v\)?
- Fixed reference value
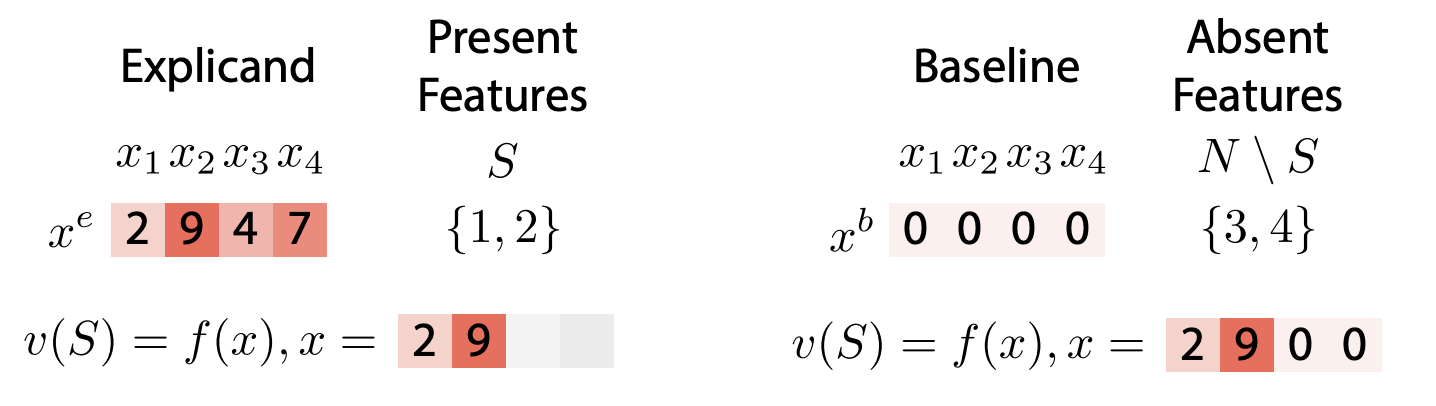
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]
\(v_f(S,x) = f(x_S,\mathbb x^{b}_{\bar{S}})\)
Easy, cheap
\( (x_S,x^b_{\bar{S}})\not\sim p_X\)
(x_S,x^b_{\bar{S}})
x
Question 1:
How should (can) we choose the function \(v\)?
- Conditional Data Distribution
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]Question 1:
How should (can) we choose the function \(v\)?
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)
\((x_S,\tilde{X}_{\bar{S}})\)
\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)
"True to the data"
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]- Conditional Data Distribution
- Difficult/expensive
- "Breaks" the Null axiom:
if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)
Question 1:
How should (can) we choose the function \(v\)?
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)
\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)
(x_S,\tilde{X}_{\bar{S}})
x_S
x
"True to the data"
- Difficult/expensive
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]- Conditional Data Distribution
- "Breaks" the Null axiom:
if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)
Question 1:
How should (can) we choose the function \(v\)?
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S]\)
\( (x_S,\tilde{X}_{\bar{S}})\sim p_X\)
(x_S,\tilde{X}_{\bar{S}})
x_S
x
"True to the data"
- Difficult/expensive
Alternative: learn a model \(g_\theta\) for the conditional expectation
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})|X_S = x_S] \approx g_\theta (x,S)\)
[Frye et al, 2021]\(g_\theta (x,S):\) ViT : transformers
[Covert et al, 2023][Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Teneggi et al, 2023][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]- Conditional Data Distribution
- "Breaks" the Null axiom:
if \(f(x_i,x_{i^C}) = f(x'_i,x_{i^C}) ~\forall x_{i^C}~\not\Rightarrow \phi_i(f) \neq 0\)
Question 1:
How should (can) we choose the function \(v\)?
- Marginal Data Distribution
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})]\)
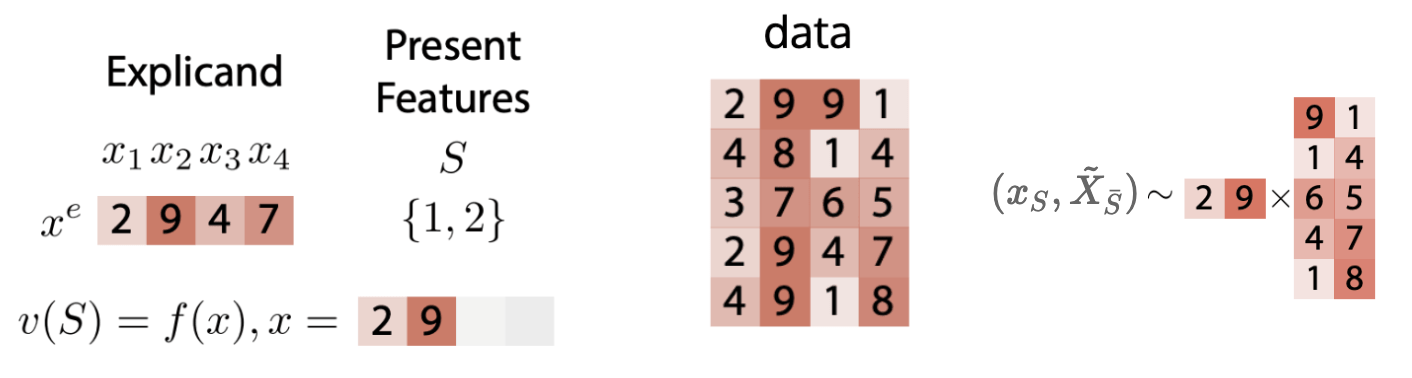
- \( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)
- Easier than conditional
- ``true to the model''
maintains Null axiom
- can hide correlations in the data
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022] [Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]\(=~~ \mathbb{E}[f(X)|do(S)]\)
(interventional expectation)
Question 1:
How should (can) we choose the function \(v\)?
- National Health and Nutrition Examination Survey (NHANES)
[Chen et al, True to the model or true to the data? 2020](mortality prediction)
Example
X = (Age,IR,WaistC,BP,BMI)
\(f(x) = \beta^\top x\), with \(\beta_5 = 0\)
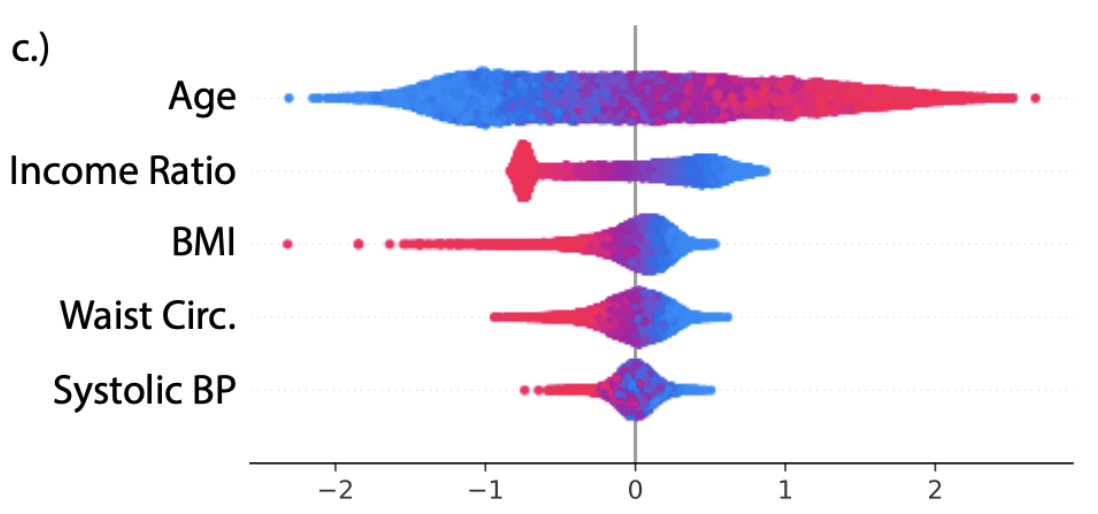
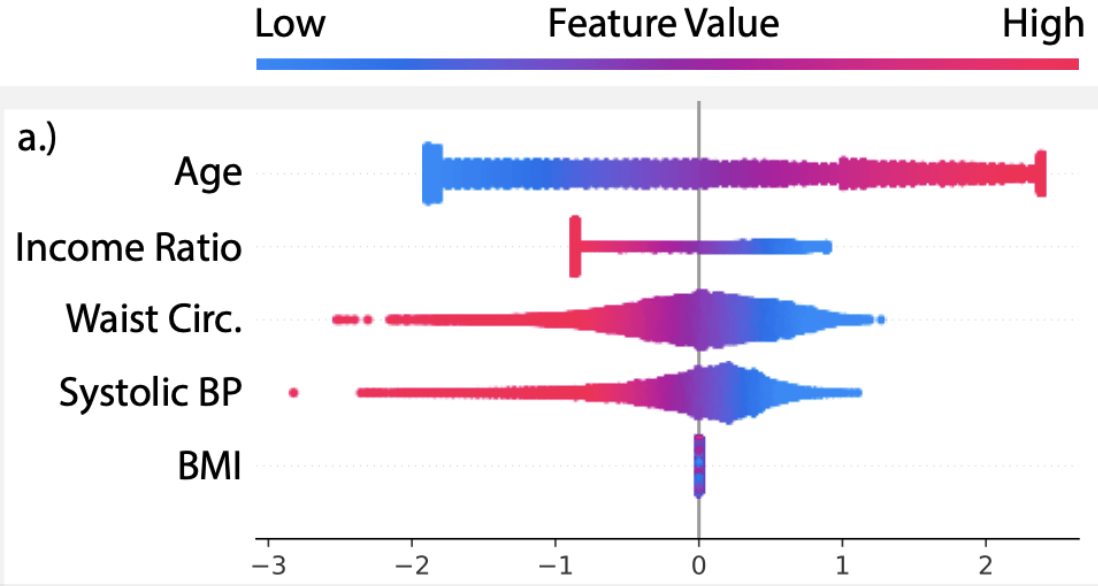
- Auditing a predictor?
(e.g. loan recommendations?) - Feature discovery/bias analysis?
Question 1:
How should (can) we choose the function \(v\)?
Linear model (approximation)
\(v_f(S,x) = \mathbb{E} [f(x_S,\tilde{X}_{\bar{S}})] \approx f(x_S,\mathbb{E}[\tilde{X}_{\bar{S}}])\)
\( (x_S,\tilde{X}_{\bar{S}})\not\sim p_X\)
except in linear models
(and feature independence)
Easiest, popular in practice
[Chen et al, Algorithms to estimate Shapley value feature attributions, 2022]
[Aas et al, 2019] [Lundberg & Lee, 2017][Frye et al, 2021][Janzing et al, 2019][Chen et al, 2020]
Shapley Explanations for ML
X \in \mathcal X \subset \mathbb R^n
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
Question 1:
How should (can) we choose the function \(v\)?
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Y\in \mathcal Y = [C]
f(X) = \hat{Y} \approx Y
Question 2:
How can we (when) compute \(\phi_i(v)\)?
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Question 2:
How can we (when) compute \(\phi_i(v)\)?
intractable.. \(\mathcal O (2^n)\)
\displaystyle \phi_i(v) = \frac{1}{n!} \sum_{\pi \subseteq \Pi(n)} \left[ v(\text{Pre}^i(\pi)\cup \{i\}) - v(\text{Pre}^i(\pi)) \right]
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014] [Datta el at, 2016]
Weighted Least Squares (kernelSHAP )
\displaystyle \phi_i(v) = \argmin_{\color{red}\beta\in\mathbb R^{n+1}} \sum_{S \subseteq [n]} \omega(S) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2
Monte Carlo Sampling
\displaystyle \phi_i(v) = \sum_{S' \sim w(S)} \left[ v(S'\cup \{i\}) - v(S') \right]
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
[Jethani et al, 2021]
Weighted Least Squares (kernelSHAP )
Weighted Least Squares, amortized ( FastSHAP )
\displaystyle \Phi_\text{fastShap} = \argmin_{\color{red}\phi_\theta:\mathcal X\to \mathbb R^n}~~ \underset{X}{\mathbb E} ~\sum_{y\in[k]} ~~ \sum_{S \subseteq [n]} \omega(S) (v(S,y) - \sum_{j\in S}{\color{red}\phi_\theta(X,y)_j})^2
... and stochastic versions [Covert et al, 2024]
Question 2:
How can we (when) compute \(\phi_i(v)\)?
\displaystyle \phi_i(v) = \argmin_{\color{red}\beta\in\mathbb R^{n+1}} \sum_{S \subseteq [n]} \omega(S) (v(S) - {\color{red}\beta_0} - \sum_{j\in S}{\color{red}\beta_j})^2
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
[Lundberg and Lee, 2017] [Strumbelj & Kononenko, 2014][Chen et al, 2020]
-
Linear models \(f(x) = \beta^\top x \)
Closed-form expressions (for marginal distributions and baselines)
\( \phi_i(f,x) = \beta_i (x_i-\mu_i ) \)
(also for conditional if assuming Gaussian features)
Tree models
[Lundberg et al, 2020]
Polynomial time algorithm (exact) (TreeSHAP) for \(\phi_i(f)\)
\(\mathcal O(N_\text{trees}N_\text{leaves} \text{Depth}^2)\)
(about the model)
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
-
Local models
(about the model)
[Chen et al, 2019]
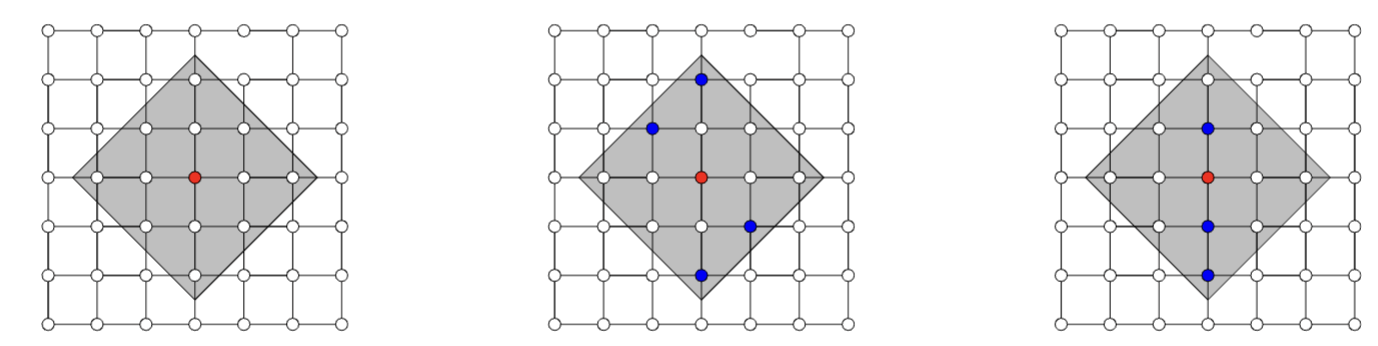
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure
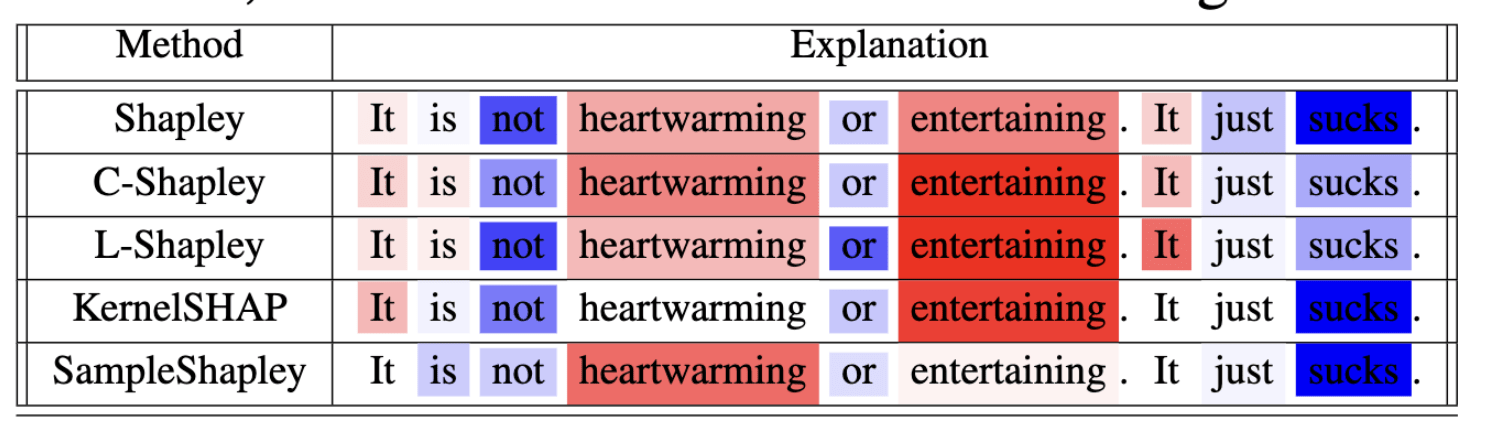
L-Shap
C-Shap
\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
-
Local models
(about the model)
[Chen et al, 2019]
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure
\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)
Correct approximations (informal statement)
Let \(S\subset \mathcal N_k(i)\). If, for any \(T\subseteq S\setminus \{i\}\), \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T) \) and \((X_i \perp\!\!\!\perp X_{[n]\setminus S} | X_T,Y) \)
Then \(\hat{\phi}^k_i(v) = \phi_i(v)\)
(and approximately bounded otherwise, controlled)
\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
-
Local models
(about the model)
[Chen et al, 2019]
Observation: Restrict computation of \(\phi_i(f)\) to local areas of influence given by a graph structure
\(\Rightarrow\) complexity \(\mathcal O(2^k n)\)
\displaystyle \hat{\phi}^k_i(v) = \frac{1}{|\mathcal N_k(i)|} \sum_{S\subseteq\mathcal N_k(i)\setminus i } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
-
Hierarchical Shapley (h-Shap)
[Teneggi et al, 2022]
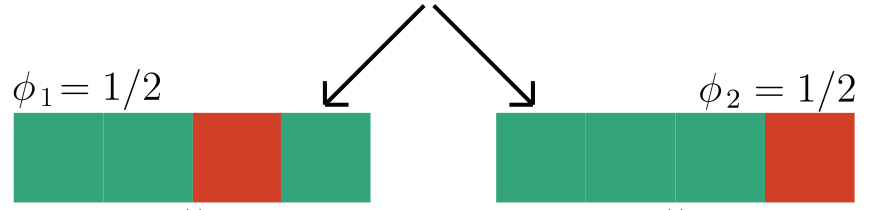
Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,{X}_{-i}) = 1\) (A1)
{\huge)} = 0
{f}\huge(
{\huge)} = 1
{f}\huge(
Example:
f(x) = 1
if contains a sick cell
x
{f}\huge(
{\huge)} = 0
(about the model)
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
(about the model)
\gamma = 2
-
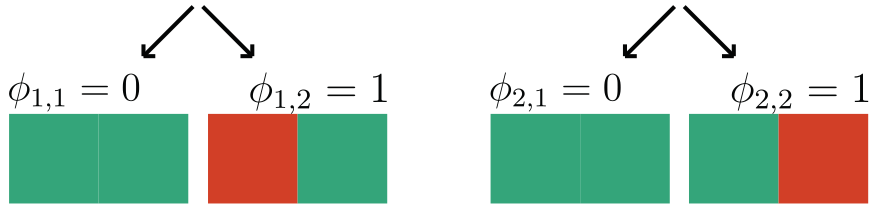
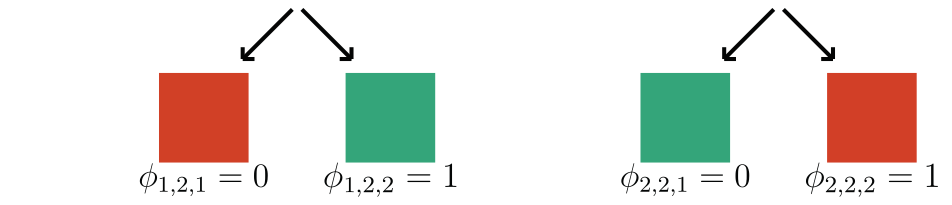
Hierarchical Shapley (h-Shap)
[Teneggi et al, 2022]
Under A1, \(\phi^\text{h-Shap}_i(f) = \phi_i(f)\)
Bounded approximation as deviating from A1
2. Correct approximation (informal)
1. Complexity \(\mathcal O(2^\gamma k \log n)\)
Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,{X}_{-i}) = 1\) (A1)
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
(about the model)
-
Hierarchical Shapley (h-Shap)
[Teneggi et al, 2022]
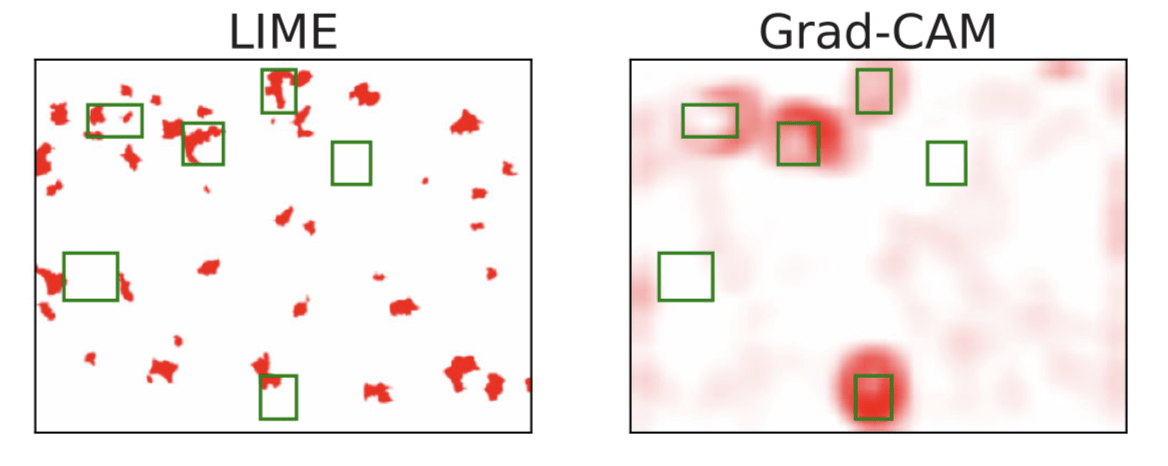
Observation: \(f(x) = 1 \Leftrightarrow \exist~ i: f(x_i,{X}_{-i}) = 1\) (A1)
Question 2:
How can we (when) compute \(\phi_i(v)\) if we know more?
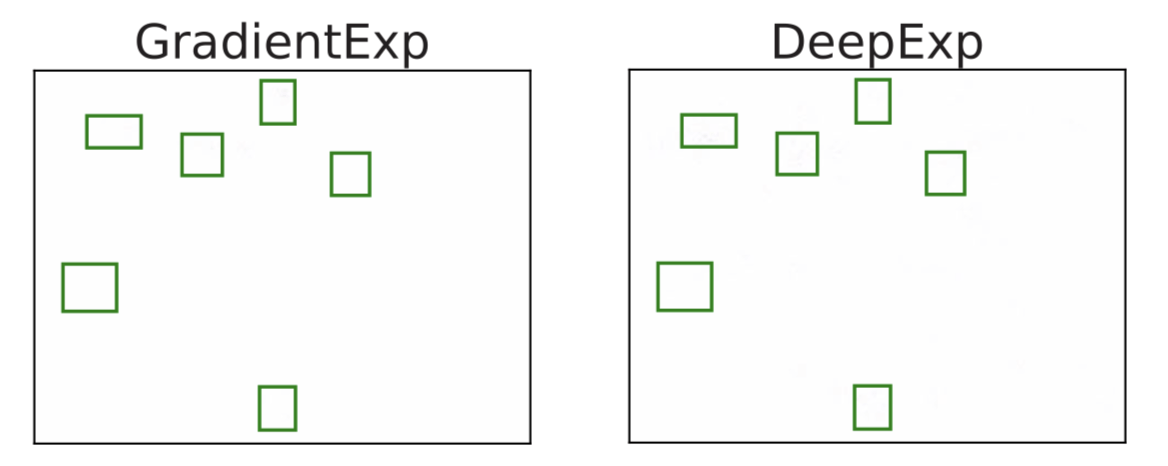
Shapley Approximations for Deep Models
(about the model)
DeepLift (Shrikumar et al, 2017): biased estimation of baseline Shap
DeepShap (Chen et al, 2021): biased estimation of marginal Shap
DASP (Ancona et al, 2019) Uncertainty propagation for baseline (zero) Shap
assuming Gaussianity and independence of features
Shapnets [Wang et al, 2020]: Computation for small-width networks
... not an exhaustive list!
Transformers (ViTs) [Covert et al, 2023]: leveraging attention to fine-tune a surrogate model for Shap estimation
Shapley Explanations for ML
Question 2:
How can we (when) compute \(\phi_i(v)\)?
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
X \in \mathcal X \subset \mathbb R^n
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
Question 1:
How should (can) we choose the function \(v\)?
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v(S\cup \{i\}) - v(S) \right]
Y\in \mathcal Y = [C]
f(X) = \hat{Y} \approx Y
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Interpretability as Conditional Independence
Explaining uncertainty via Shapley Values [Watson et al, 2023]
\displaystyle \phi_i(v) = \sum_{S\subseteq [n]\setminus \{i\} } w(S) \left[ v_\text{KL}(S\cup \{i\}) - v_\text{KL}(S) \right]
with \(v_\text{KL}(S,x) = -D_\text{KL}(~p_{\hat Y|x} ~||~ p_{\hat Y|x_s}~)\)
Theorem (informal)
\(\hat Y \perp\!\!\!\perp X_i | X_s = x_s ~~\Rightarrow~~ v_\text{KL}(S\cup\{i\},x) - v_\text{KL}(S,x) = 0\)
how many bore bits do we get by adding \(x_i\) to \(x_S\)?
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Interpretability as Conditional Independence
-
SHAP-XRT: Shapley meets Hypothesis Testing [Teneggi et al, 2023]
H^0_{{i},S}:~ (f(\tilde{X}_{S\cup \{{i}\}}) ) \overset{d}{=} (f(\tilde{X}_S) )
\text{reject} ~\Rightarrow~ i=2 \text{: important}
H^0_{i=2,S=\{1,3,4\}}
i=1
i=2
i=3
i=4
Testing procedure:
\(p_{i,S} \leftarrow \text{eXplanation Randomization Test}\)
via access to \({X}_{\bar{S}} \sim p_{X_{\bar{S}}|x_s}\)
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Interpretability as Conditional Independence
-
SHAP-XRT: Shapley meets Hypothesis Testing [Teneggi et al, 2023]
H^0_{{i},S}:~ (f(\tilde{X}_{S\cup \{{i}\}}) ) \overset{d}{=} (f(\tilde{X}_S) )
Theorem (informal)
For \(f:\mathcal X \to [0,1], ~~ p_{i,S}\leq 1- \mathbb E [v(S\cup i) - v(S)] \)
Thus, large \(\mathbb E [v(S\cup i) - v(S)] ~ \Rightarrow \) reject \(H^0_{i,S}\)
Question 3:
What do \(\phi_i(v)\) say (and don't) about the problem?
Interpretability as Conditional Independence
\displaystyle H^0_\text{global}
\displaystyle p_\text{global} = 2 \sum_{S \subseteq [n]\setminus i} w_{S} ~ p_{i,S}
Then, under ,
p_\text{global} \leq 2( 1-\phi_i(x))
Theorem (informal)
-
SHAP-XRT: Shapley meets Hypothesis Testing [Teneggi et al, 2023]
H^0_{{i},S}:~ (f(\tilde{X}_{S\cup \{{i}\}}) ) \overset{d}{=} (f(\tilde{X}_S) )
Last Question 3': Should we just focus on CIT?Is the piano important for \(\hat Y = \text{cat}\), given that there is a cute mammal in the image?
Local Conditional Importance
\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]
features with concepts \(S\cup \{i\}\)
features with concepts \(S\)
[Teneggi et al, Testing semantic importance via betting, 2024]
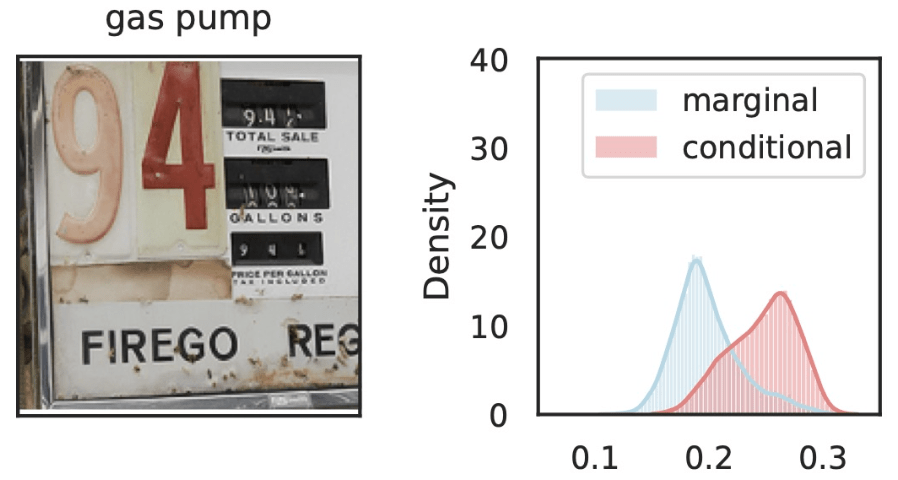
\(\hat{Y}_\text{gas pump}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
\(Z_j=\)
Local Conditional Importance
\(\tilde{Z}_S = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, Z_\text{trumpet}, Z_\text{fire}, \dots ] \)
\(S\)
\(\tilde{Z}_{S\cup j} = [z_\text{text}, z_\text{old}, z_\text{dispenser}, Z_\text{trumpet}, Z_\text{Fire}, \dots ] \)
\(S\)
\(j\)
\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]
Last Question 3': Should we just focus on CIT?[Teneggi et al, Testing semantic importance via betting, 2024]
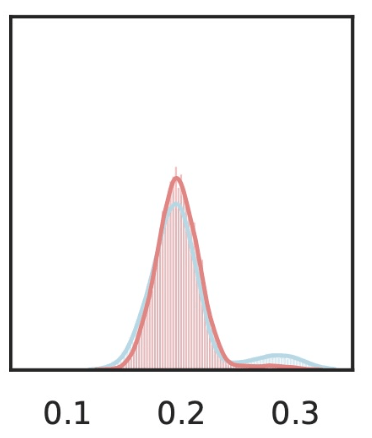
\(\hat{Y}_\text{gas pump}\)
\(\hat{Y}_\text{gas pump}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
Local Conditional Importance
\(Z_j=\)
\(Z_j=\)
\(\tilde{Z}_S = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, Z_\text{trumpet}, Z_\text{fire}, \dots ] \)
\(\tilde{Z}_{S\cup j} = [z_\text{text}, z_\text{old}, Z_\text{dispenser}, z_\text{trumpet}, Z_\text{Fire}, \dots ] \)
\(S\)
\(S\)
\(j\)
\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]
Last Question 3': Should we just focus on CIT?[Teneggi et al, Testing semantic importance via betting, 2024]
Local Conditional Importance
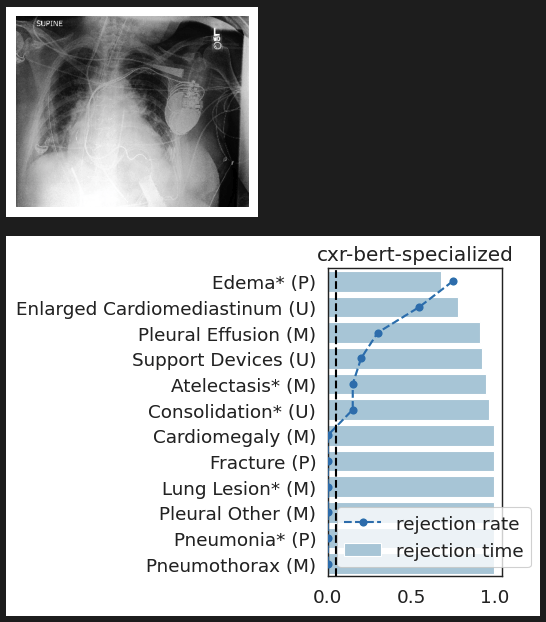
Last Question 3': Should we just focus on CIT?[Teneggi et al, Testing semantic importance via betting, 2024]
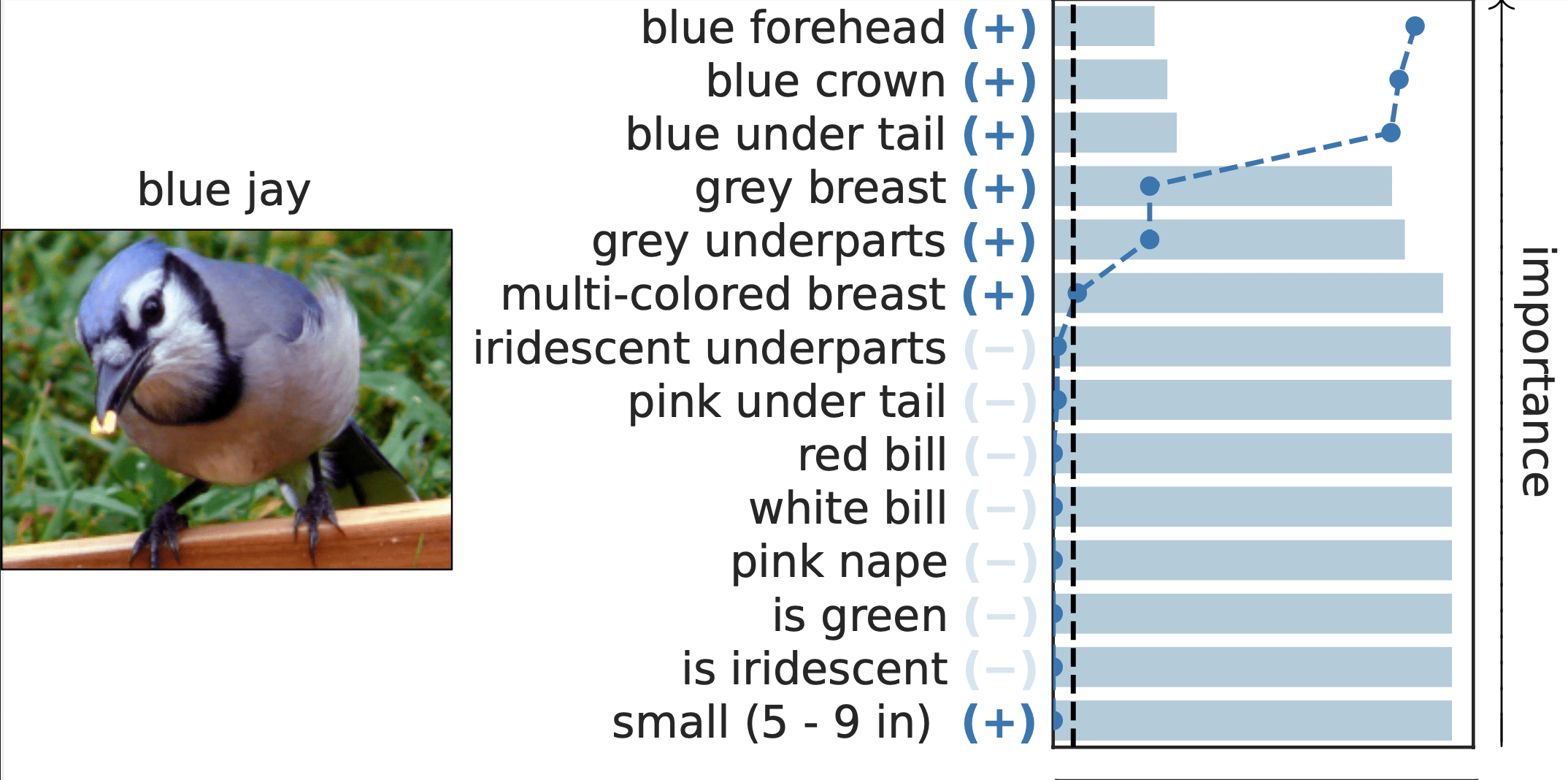
Important Semantic Concepts
(Reject \(H_0\))
Unimportant Semantic Concepts
(Fail to reject)
rejection time
rejection rate
0.0
1.0
\[H^{j,S}_0:~ f({\tilde H_{S \cup \{j\}}}) \overset{d}{=} f(\tilde H_S) \]
Conclusions
- Shapley Values are one of the most popular wrapper-explanation methods
- Defined axiomatically \(\Rightarrow\) clear what they satisfy and don't satisfy; analytically clear objective
Pros
- Amenable to using data and model properties for fast computation
- Choosing distributions to sample from is important and problem-dependent: "true to the model" vs "true to the data"
Cons
- Unclear if those axioms are what we should require from interpretability methods
Foundations of Interpretable AI
PART I: Motivation and Post-hoc Methods
(8:00 - 9:00 am)
Aditya Chattopadhyay (Amazon)
PART II: Shapley Value based Methods
(9:15 - 10:15 am)
Jeremias Sulam (Johns Hopkins)
PART III: Interpretable by Design Methods
(10:30 - 11:30 am)
René Vidal (Penn)
Coffee break
(10:15- 10:30 am)
Coffee break
(9:00- 9:15 am)
ICCV Foundations of Interpretable AI - Shapley
By Jeremias Sulam
