Modern problems in trustworthy medical imaging
Jeremias Sulam


June 2025


50 years ago ...
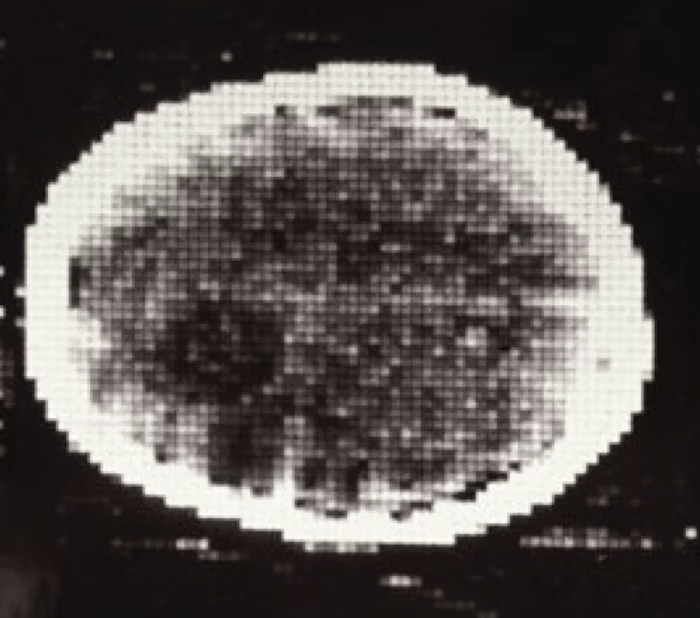
first CT scan


ELECTRIC & MUSICAL INDUSTRIES
50 years ago ...

imaging
diagnostics
complete hardware & software description
human expert diagnosis and recommendations

imaging was "simple"
... 50 years forward

Data

Compute & Hardware



Sensors & Connectivity







Research & Engineering
... 50 years forward


data-driven imaging
automatic analysis and rec.
societal implications
Data

Compute & Hardware



Sensors & Connectivity







Research & Engineering






Data

Compute & Hardware



Sensors & Connectivity







Research & Engineering




... 50 years forward



data-driven imagingautomatic analysis and rec.societal implicationsProblems in trustworthy biomedical imaging
inverse problems
uncertainty quantification
robustness
generalization
policy & regulation
Demographic fairness
hardware & protocol optimization
model-agnostic interpretability



inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
demographic fairness
hardware & protocol optimization
data-driven imaging
automatic analysis and rec.
societal implications
Problems in trustworthy biomedical imaging



Demographic fairness
Inputs (features): \(X\in \mathcal X \subset \mathbb R^d\)
Responses (labels): \(Y\in \{0,1\}\)
Sensitive attributes: \(Z \in \mathbb R^k \) (sex, race, age, etc)
Random variables sampled: \((X,Y,Z) \sim \mathcal D\)
Eg: \(Z_1: \) biological sex, \(X_1: \) BMI, then
\( g(Z,X) = \boldsymbol{1}\{Z_1 = 1 ~\texttt{and}~ X_1 > 35 \}: \) women with BMI > 35
Goal: ensure that \(f\) is fair w.r.t groups \(g \in \mathcal G\)
Demographic fairness
Group memberships \( \mathcal G = \{ g(X,Z) \mapsto \{0,1\} \} \)
Predictor \( f(X) : \mathcal X \to [0,1]\) (e.g. likelihood of X having disease Y)
-
Group/Associative Fairness
Predictors should not have very different (error) rates among groups
[Calders et al, '09][Zliobaite, '15][Hardt et al, '16]
-
Individual Fairness
Similar individuals/patients should have similar outputs
[Dwork et al, '12][Fleisher, '21][Petersen et al, '21]
-
Causal Fairness
Predictors should be fair in a counter-factual world
[Nabi & Shpitser, '18][Nabi et al, '19][Plecko & Bareinboim, '22]
-
Multiaccuracy/Multicalibration
Predictors should be approximately unbiased/calibrated for every group
[Kim et al, '20][Hebert-Johnson et al, '18][Globus-Harris et at, 22]
Demographic fairness
Demographic fairness
-
Group/Associative Fairness
Predictors should not have very different (error) rates among groups
Equal Opportunity
Equal True Positive Rates (TPR) across groups
\(\mathbb P[\hat Y=1 | Y=1, G_{\texttt{age}\leq 60}=0] = \mathbb P[\hat Y = 1 | Y=1, G_{\texttt{age}>60}=1]\)
\(\Delta \text{TPR}_\text{age} = \left| \text{TPR}_{\texttt{age}\leq 60} - \text{TPR}_{\texttt{age}>60}\right| \leq \alpha \)
Demographic fairness
-
Group/Associative Fairness
Predictors should not have very different (error) rates among groups
Multiaccuracy
Similar accuracy across different groups
-
Multiaccuracy/Multicalibration
Predictors should be approximately unbiased/calibrated for every group
\(\text{MA} (f,g) = \big| \mathbb E [ g(X,Z) (f(X) - Y) ] \big| \)
\(f\) is \(\alpha\)-multiaccurate if \( \max_{g\in\mathcal G} \text{MA}(f,g) \leq \alpha \)
Demographic fairness
Multiaccuracy
Similar accuracy across different groups
\(\text{MA} (f,g) = \big| \mathbb E [ g(X,Z) (f(X) - Y) ] \big| \)
\(f\) is \(\alpha\)-multiaccurate if \( \max_{g\in\mathcal G} \text{MA}(f,g) \leq \alpha \)
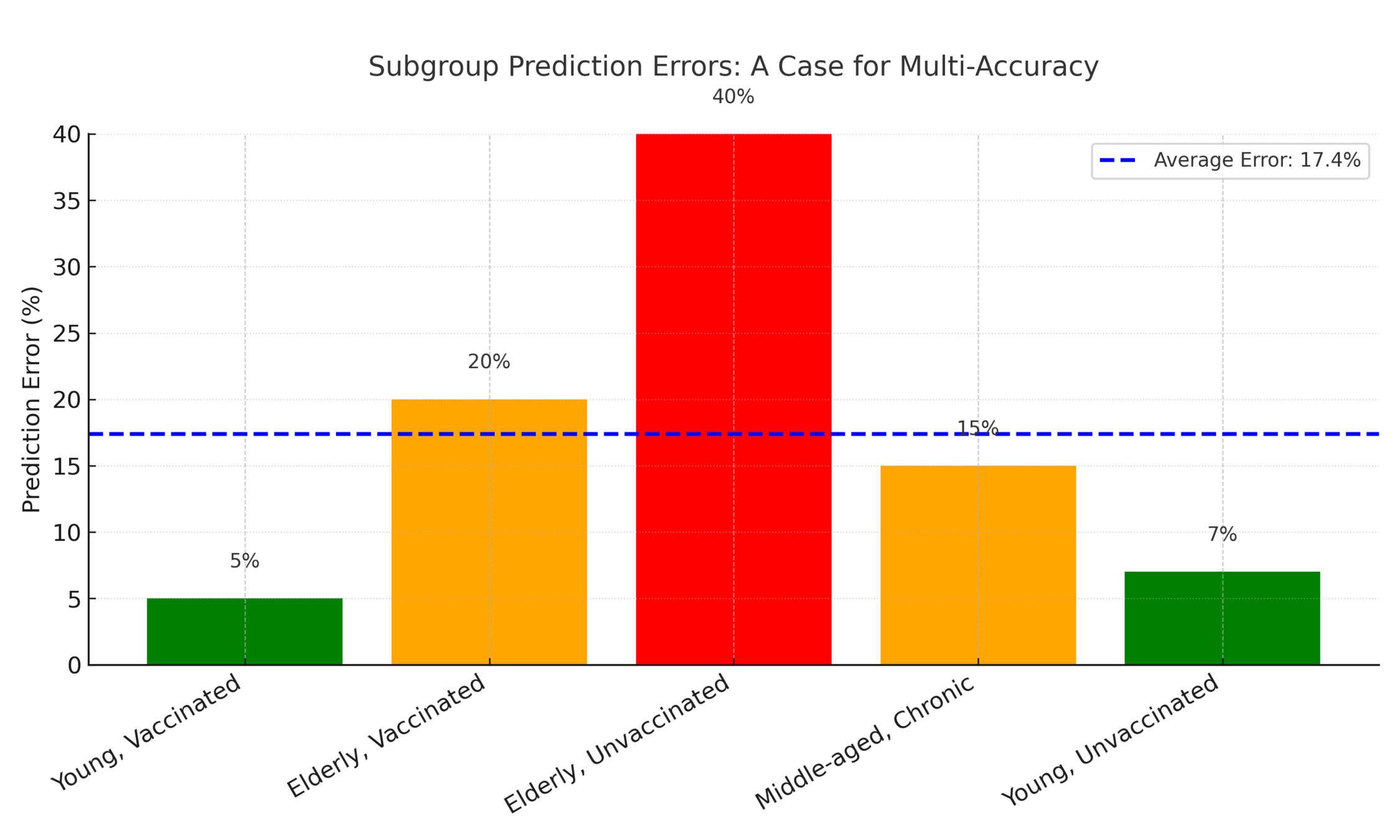
Example: predicting high risk of complications from flu based on clinical features
Demographic fairness
Multiaccuracy
Similar accuracy across different groups
\(\text{MA} (f,g) = \big| \mathbb E [ g(X,Z) (f(X) - Y) ] \big| \)
\(f\) is \(\alpha\)-multiaccurate if \( \max_{g\in\mathcal G} \text{MA}(f,g) \leq \alpha \)

Example: predicting high risk of complications from flu based on clinical features
Observation:
Evaluation for fairness notions requires samples over \((X,Y,Z)\)
Demographic fairness
Multiaccuracy
Similar accuracy across different groups
\(\text{MA} (f,g) = \big| \mathbb E [ g(X,Z) (f(X) - Y) ] \big| \)
\(f\) is \(\alpha\)-multiaccurate if \( \max_{g\in\mathcal G} \text{MA}(f,g) \leq \alpha \)

Example: predicting high risk of complications from flu based on clinical features
Observation:
Evaluation for fairness notions requires samples over \((X,Y,Z)\)
Problem: This is not always possible...


Problem: This is not always possible...


Problem: This is not always possible...
sex and race attributes missing
- We might want to conceal \(Z\) on purpose, or might need to
?
?
?
?
?
We observe samples over \((X,Y)\) to obtain \(\hat Y = f(X)\) for \(Y\)
Fairness in partially observed regimes
\( \text{MSE}(f) = \mathbb E [(Y-f(X))^2 ] \)
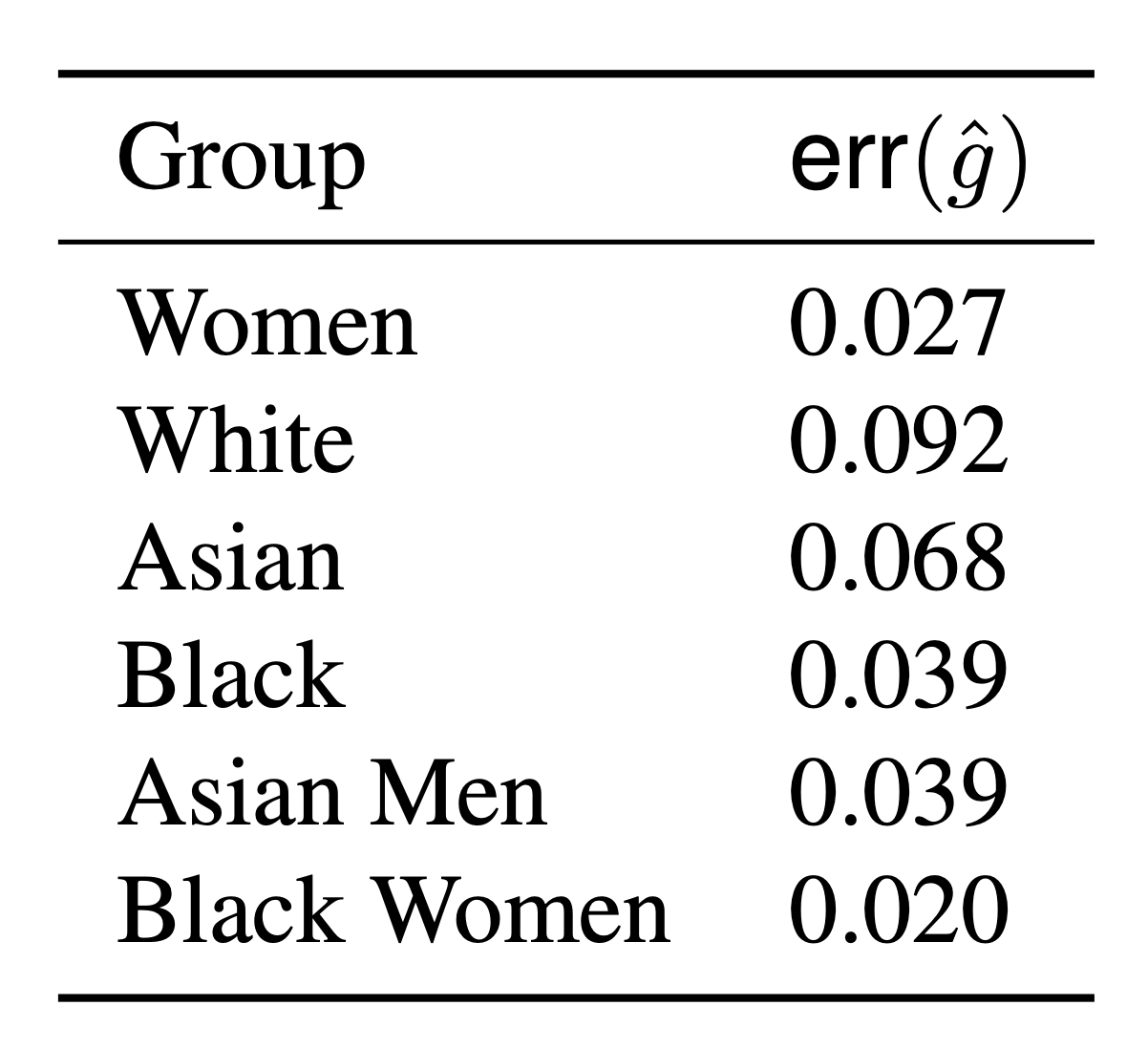
A developer provides us with proxies \( \color{Red} \hat{g} : \mathcal X \to \{0,1\} \)
\( \text{err}(\hat g) = \mathbb P [({\color{Red}\hat g(X)} \neq {\color{blue}g(X,Z)} ] \)
Can we use \(\hat g\) to measure (and correct) for fairness metrics?
[Awasti et al, '21][Kallus et al, '22][Zhu et al, '23][Bharti et al, '24]
We observe samples over \((X,Y)\) to obtain \(\hat Y = f(X)\) for \(Y\)
Fairness in partially observed regimes
\( \text{MSE}(f) = \mathbb E [(Y-f(X))^2 ] \)
A developer provides us with proxies \( \color{Red} \hat{g} : \mathcal X \to \{0,1\} \)
\( \text{err}(\hat g) = \mathbb P [({\color{Red}\hat g(X)} \neq {\color{blue}g(X,Z)} ] \)
[Awasti et al, '21][Kallus et al, '22][Zhu et al, '23][Bharti et al, '24]
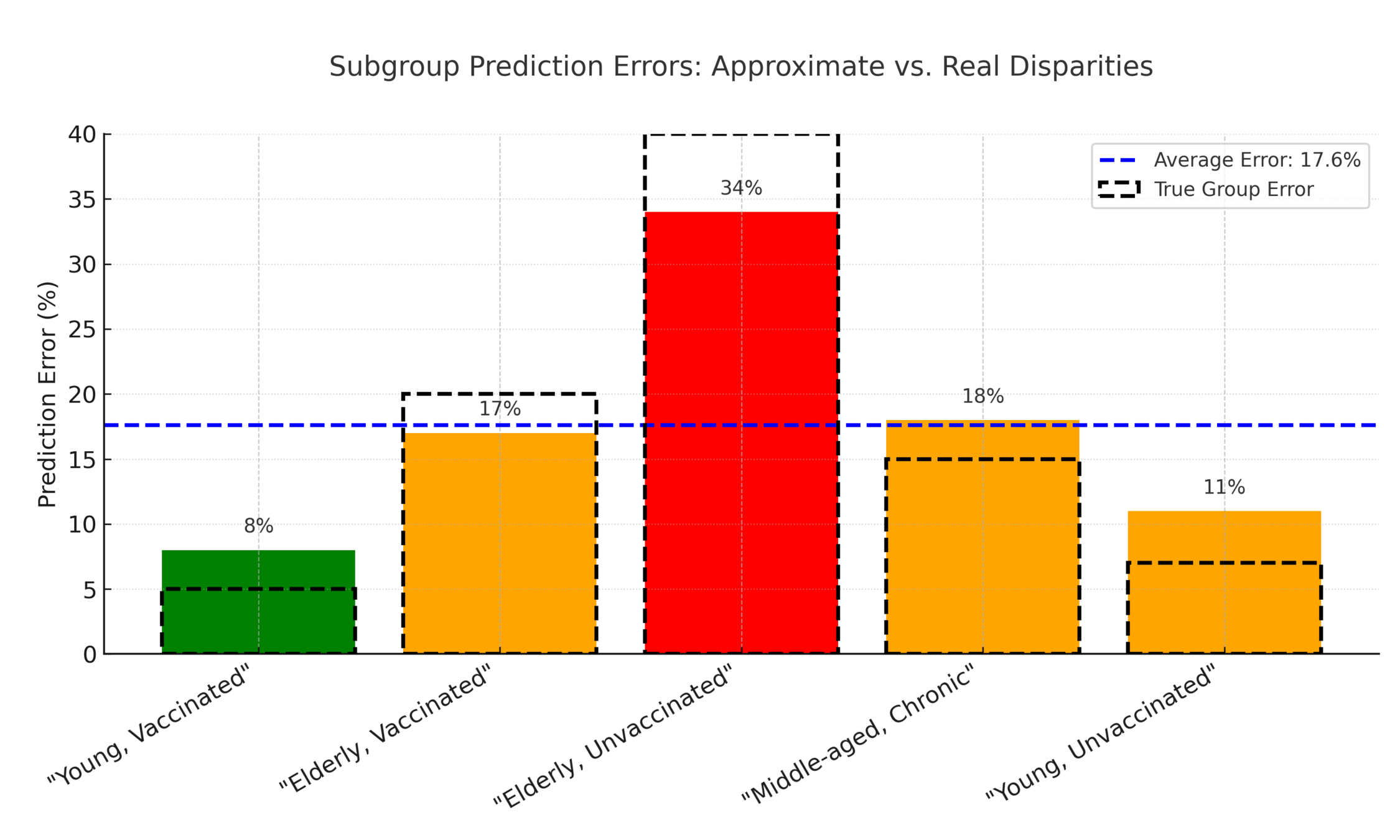
Can we use \(\hat g\) to measure (and correct) for fairness metrics?
Fairness in partially observed regimes
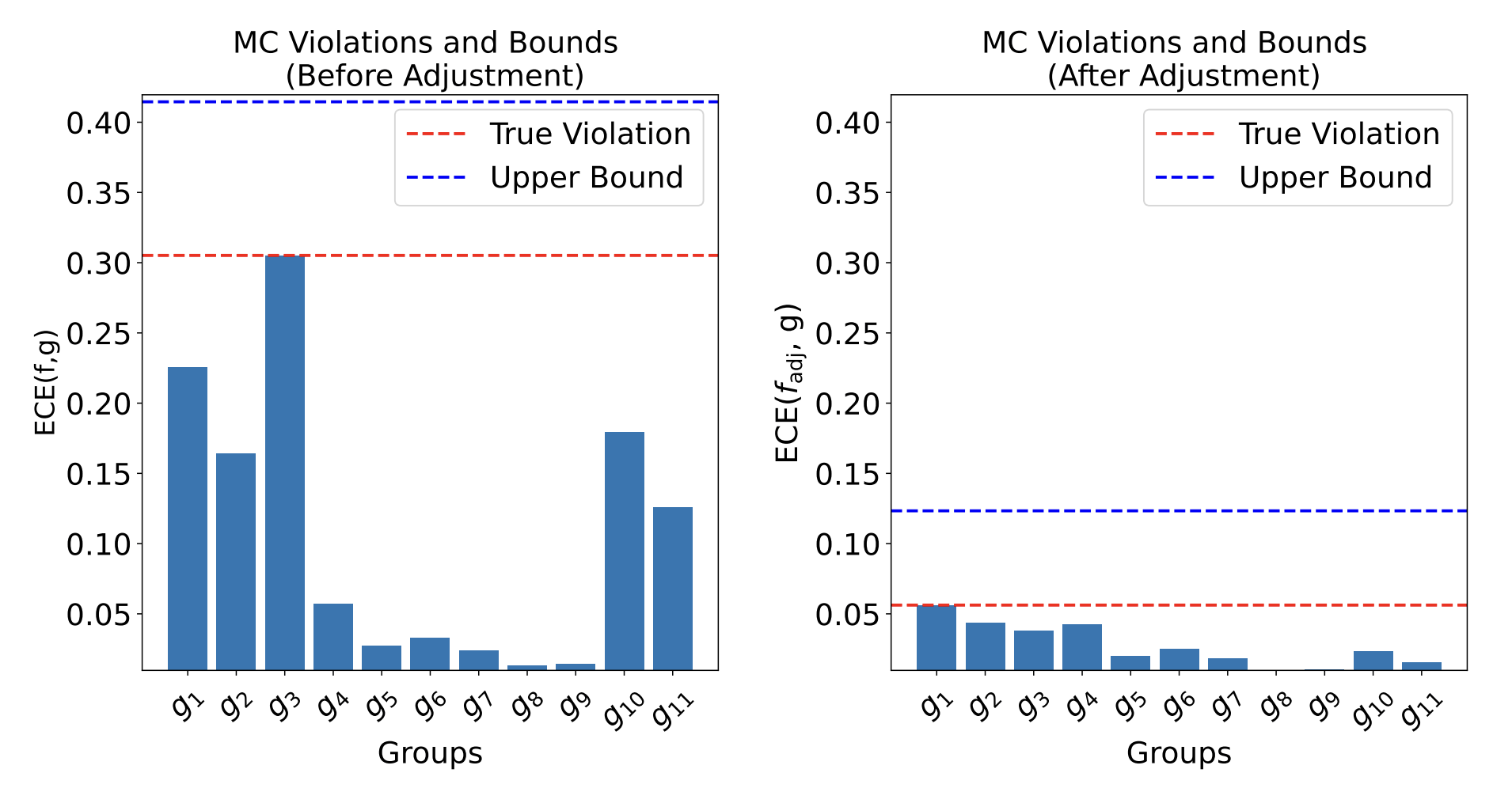
Theorem [Bharti, Clemens-Sewall, Yi, Sulam]
With access to \((X,Y)\sim \mathcal D_{\mathcal{XY}}\), proxies \( \hat{\mathcal G}\) and predictor \(f\)
\[ \max_{\color{Blue}g\in\mathcal G} \text{MA}(f,{\color{blue}g}) ~\leq ~\max_{\color{red}\hat g\in \hat{\mathcal{G}} } \text{MA}(f,{\color{red}\hat{g}}) + B(f,{\color{red}\hat g}) \]
with \(B(f,\hat g) = \min \left( \text{err}(\hat g), \sqrt{MSE(f)\cdot \text{err}(\hat g)} \right) \)
true error
worst possible error
- Practical/computable upper bounds
Fairness in partially observed regimes
- Practical/computable upper bounds
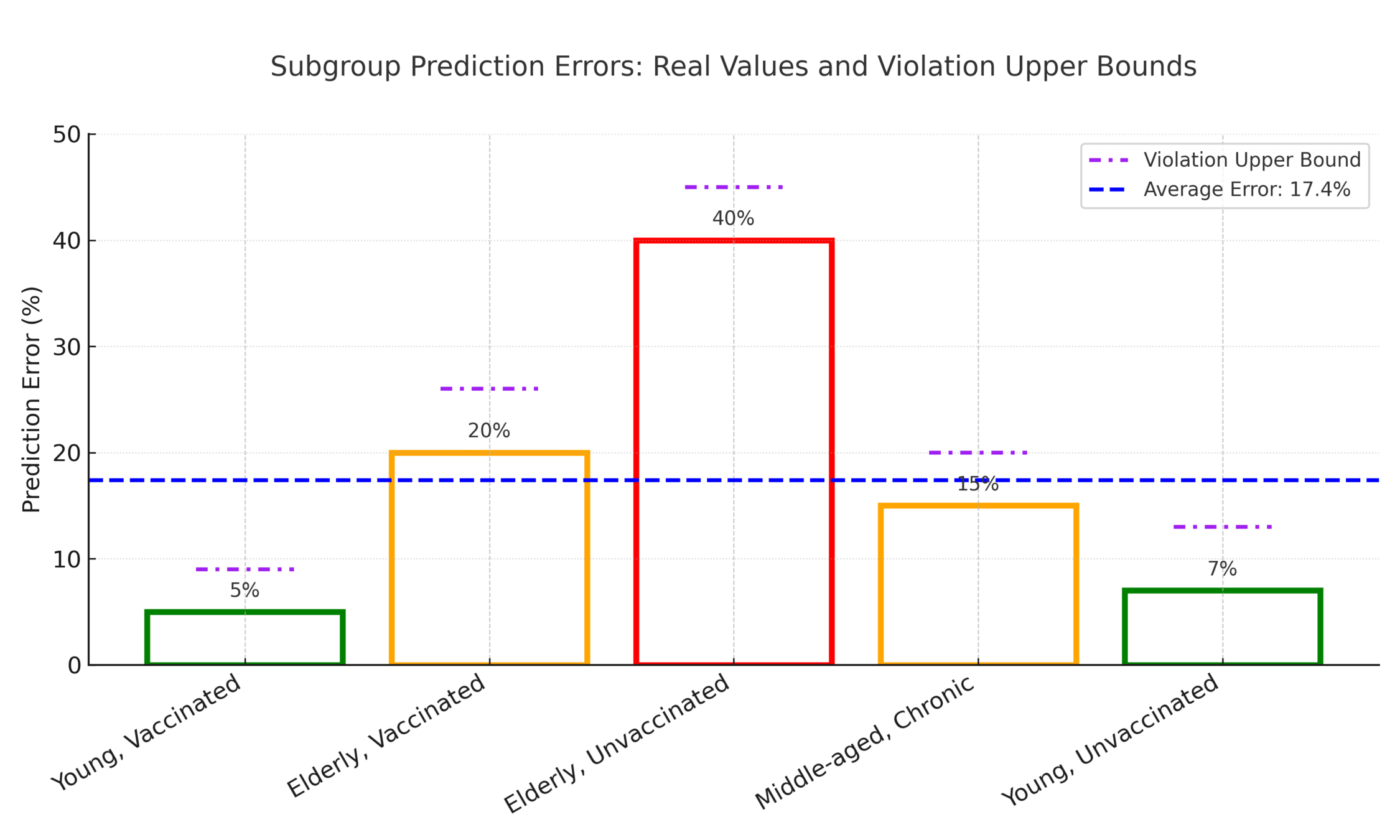
Theorem [Bharti, Clemens-Sewall, Yi, Sulam]
With access to \((X,Y)\sim \mathcal D_{\mathcal{XY}}\), proxies \( \hat{\mathcal G}\) and predictor \(f\)
\[ \max_{\color{Blue}g\in\mathcal G} MA(f,{\color{blue}g}) ~\leq ~\max_{\color{red}\hat g\in \hat{\mathcal{G}} } MA(f,{\color{red}\hat{g}}) + B(f,{\color{red}\hat g}) \]
with \(B(f,\hat g) = \min \left( \text{err}(\hat g), \sqrt{MSE(f)\cdot \text{err}(\hat g)} \right) \)
true error
worst possible error
Fairness in partially observed regimes
- Correcting w.r.t \(\hat{\mathcal G}\) provably improves upper bound
[Gopalan et al. (2022)][Roth (2022)][Bharti et al (2025)]
- Practical/computable upper bounds
Theorem [Bharti, Clemens-Sewall, Yi, Sulam]
With access to \((X,Y)\sim \mathcal D_{\mathcal{XY}}\), proxies \( \hat{\mathcal G}\) and predictor \(f\)
\[ \max_{\color{Blue}g\in\mathcal G} \text{MA}(f,{\color{blue}g}) ~\leq ~\max_{\color{red}\hat g\in \hat{\mathcal{G}} } \text{MA}(f,{\color{red}\hat{g}}) + B(f,{\color{red}\hat g}) \]
with \(B(f,\hat g) = \min \left( \text{err}(\hat g), \sqrt{MSE(f)\cdot \text{err}(\hat g)} \right) \)
true error
worst possible error
Fairness in partially observed regimes
- Correcting w.r.t \(\hat{\mathcal G}\) provably improves upper bound
[Gopalan et al. (2022)][Roth (2022)][Bharti et al (2025)]
- Practical/computable upper bounds
Theorem [Bharti, Clemens-Sewall, Yi, Sulam]
With access to \((X,Y)\sim \mathcal D_{\mathcal{XY}}\), proxies \( \hat{\mathcal G}\) and predictor \(f\)
\[ \max_{\color{Blue}g\in\mathcal G} \text{MA}(f,{\color{blue}g}) ~\leq ~\max_{\color{red}\hat g\in \hat{\mathcal{G}} } \text{MA}(f,{\color{red}\hat{g}}) + B(f,{\color{red}\hat g}) \]
with \(B(f,\hat g) = \min \left( \text{err}(\hat g), \sqrt{MSE(f)\cdot \text{err}(\hat g)} \right) \)
true error
worst possible error

Fairness in partially observed regimes
CheXpert: Predicting abnormal findings in chest X-rays
(not accessing race or biological sex)
\(f(X): \) likelihood of \(X\) having \(\texttt{pleural effusion}\)
Demographic fairness
Take-home message
- Proxies can be very useful in certifying max. fairness violations
- Can allow for simple post-processing corrections
Fairness in partially observed regimes

CheXpert: Predicting abnormal findings in chest X-rays
(not accessing race or biological sex)

\(f(X): \) likelihood of \(X\) having \(\texttt{pleural effusion}\)

Demographic fairness
Take-home message
- Proxies can be very useful in certifying max. fairness violations
- Can allow for simple post-processing corrections





inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
demographic fairness
hardware & protocol optimization
data-driven imaging
automatic analysis and rec.
societal implications
Problems in trustworthy biomedical imaging
"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."The Bitter Lesson, Rich Sutton 2019
model-agnostic interpretability
"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."The Bitter Lesson, Rich Sutton 2019

model-agnostic interpretability

-
What parts of the image are important for this prediction?
-
What are the subsets of the input \(S\in[n]\) so that \(f(x_S) \approx f(x)\)?

Interpretability in Image Classification
Predictor \(f(x)\) trained to predict \(\texttt{sick/healthy}\)
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual & causal explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..

Post-hoc Interpretability in Image Classification
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual & causal explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..

Post-hoc Interpretability in Image Classification
Post-hoc Interpretability Methods
Interpretable by
construction
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual & causal explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..

Post-hoc Interpretability in Image Classification
Post-hoc Interpretability Methods
Interpretable by
construction

efficiency
nullity
symmetry
exponential complexity
Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
Let \(G = ([n],f)\) be an \(n\)-person cooperative game with characteristic function \(f:\mathcal P([n])\to \mathbb R\)
How important is each player for the outcome of the game?
marginal contribution of player i with coalition S
Shapley values
We focus on data with certain structure:
Example:
if contains a sick cell



Hierarchical Shap (h-Shap)
Can we resolve the computational bottleneck (and when) ?
Theorem (informal)
-
h-Shap runs in linear time
-
Under A1, h-Shap \(\to\) Shapley
\(\tilde{X}_i \sim \mathcal D_{X|X_i=x_i}\)



Hierarchical Shap (h-Shap)



Hierarchical Shap (h-Shap)
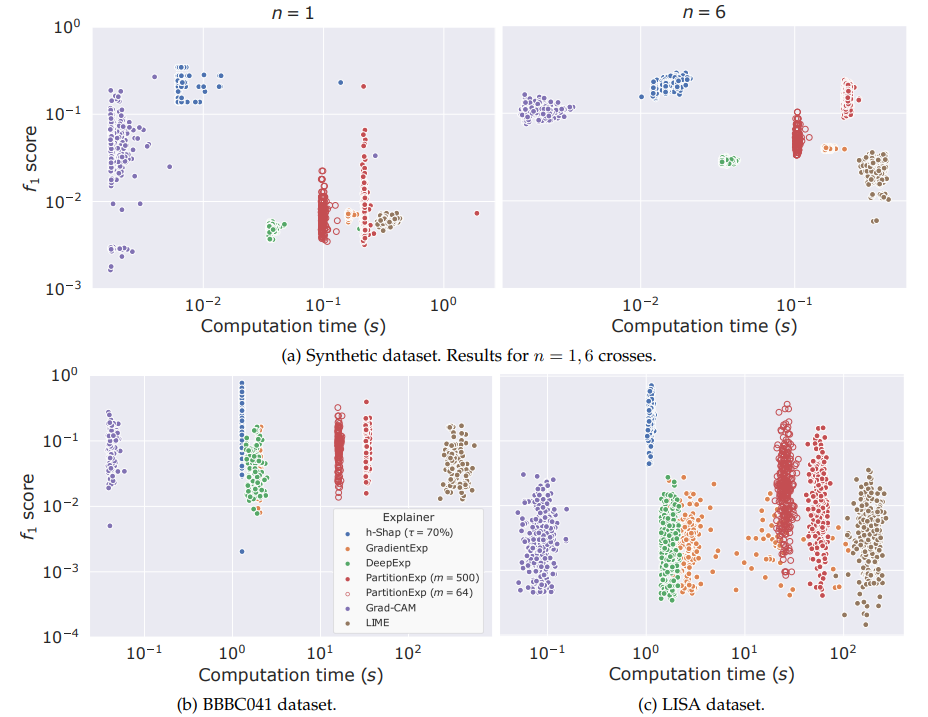




Fast hierarchical games for image explanations, Teneggi, Luster & S., IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022
Cheaper predictors via Interpretability
Cheaper predictors via Interpretability
Hemorrhage detection in head CT
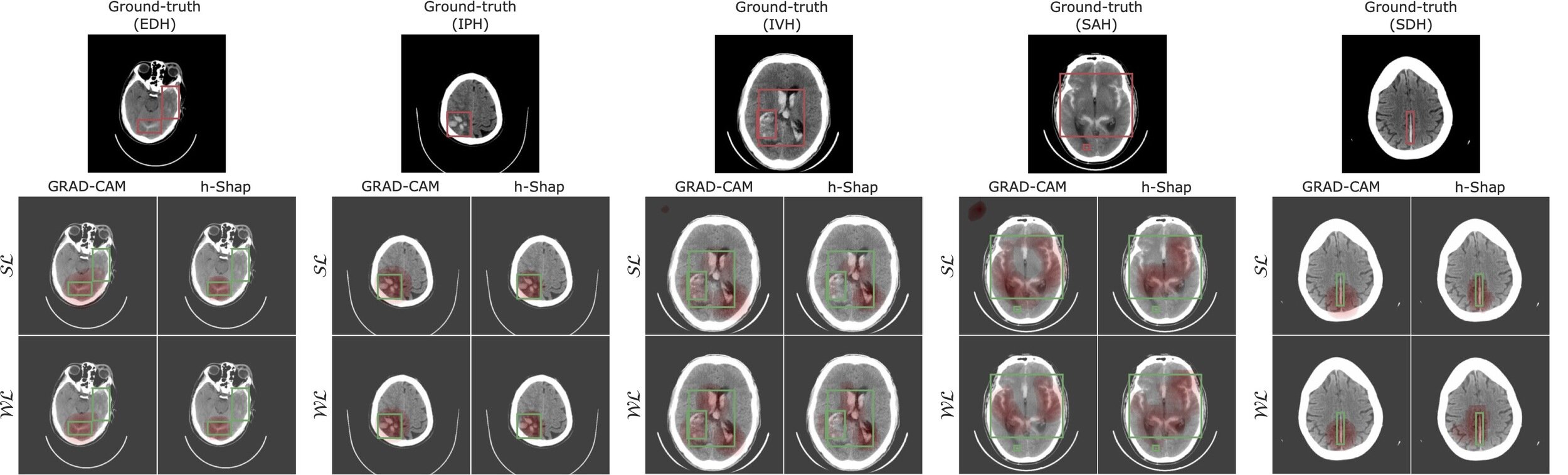





Image-by-image supervision (strong learner)
true/false
one label per image
Cheaper predictors via Interpretability
Image-by-image supervision (strong learner)

one label per image
one label per study
true/false
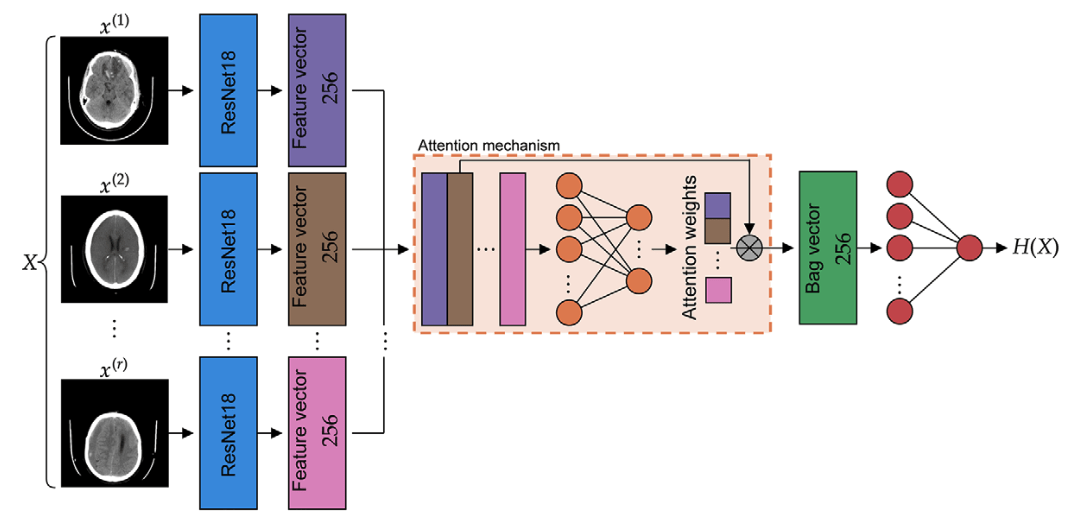
Study/volume supervision (weak learner)
true/false
Cheaper predictors via Interpretability
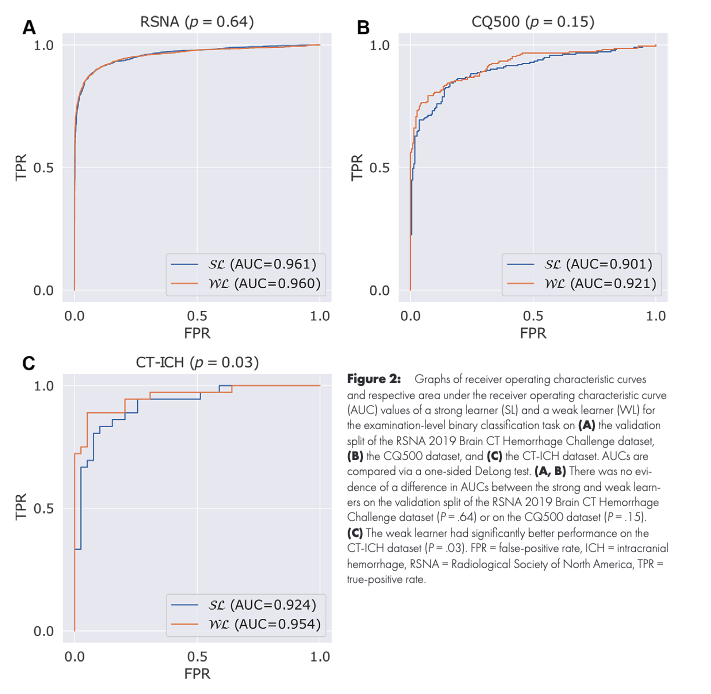

Cheaper predictors via Interpretability
-
Both methods do as well for case screaning
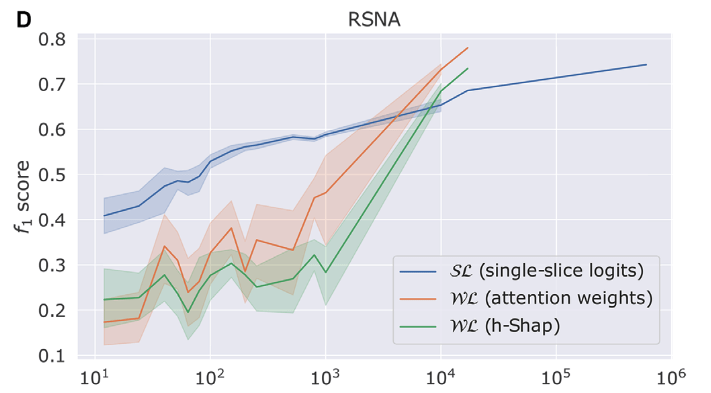
training labels
Cheaper predictors via Interpretability
-
Both methods do as well for case screaning
-
Weak learner is more label-efficient for detecting positive slices
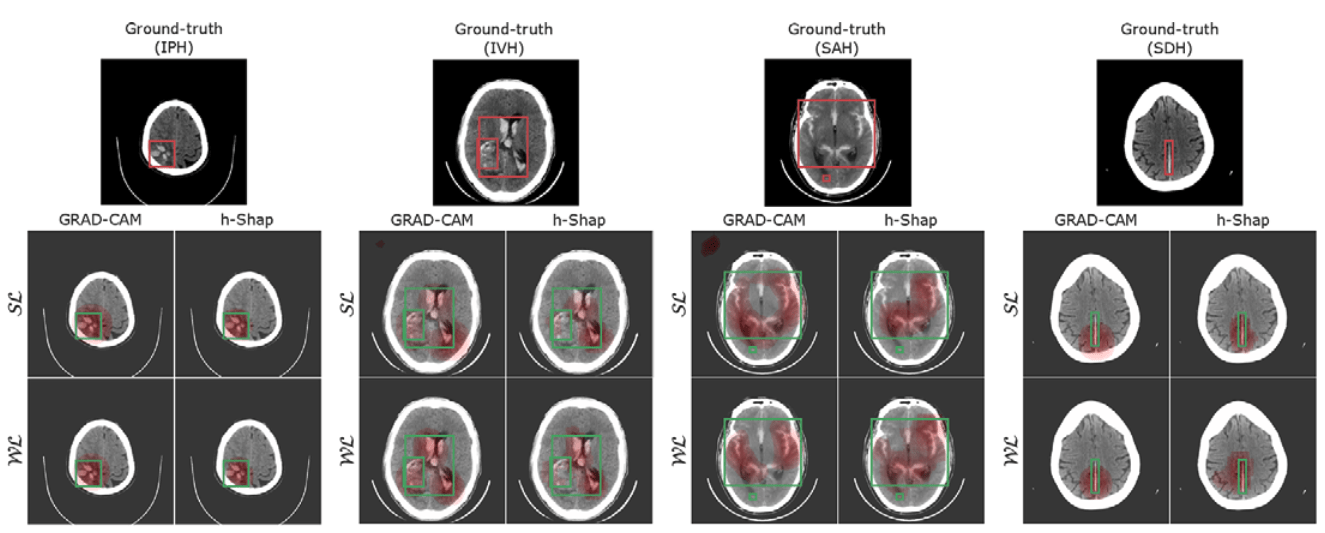
Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence.Cheaper predictors via Interpretability

Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence.

Cheaper predictors via Interpretability



inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
demographic fairness
hardware & protocol optimization
data-driven imaging
automatic analysis and rec.
societal implications
Problems in trustworthy biomedical imaging



inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
demographic fairness
hardware & protocol optimization
Problems in trustworthy biomedical imaging
data-driven imaging
automatic analysis and rec.
societal implications



inverse problems
uncertainty quantification
robustness
generalization
policy & regulation
hardware & protocol optimization
Problems in trustworthy biomedical imaging

model-agnostic interpretability
demographic fairness
data-driven imaging
automatic analysis and rec.
societal implications





Thank you for hosting me




inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
Demographic fairness
hardware & protocol optimization
data-driven imaging
automatic analysis and rec.
societal implications
Problems in trustworthy biomedical imaging
measurements
reconstruction
inverse problems
measurements
reconstruction

inverse problems

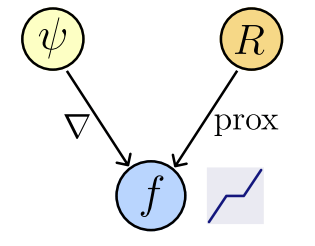
Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^\top(Ax^t-y)\right) \)
... a denoiser
\({\color{red}f_\theta}\): off-the-shelf denoiser

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Gilton, Ongie, Willett, 2019; Kamilov et al., 2023b; Terris et al., 2023; S Hurault et al. 2021, Ongie et al, 2020; ...]
Plug and Play: Implicit Priors


Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^\top(Ax^t-y)\right) \)
... a denoiser
\({\color{red}f_\theta}\): off-the-shelf denoiser

[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Gilton, Ongie, Willett, 2019; Kamilov et al., 2023b; Terris et al., 2023; S Hurault et al. 2021, Ongie et al, 2020; ...]
Plug and Play: Implicit Priors


Question 1)
What are these black-box functions computing? and what have they learned about the data?
Theorem [Fang, Buchanan, S.]
When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\), and for what \(R(x)\)?
Let \(f_\theta : \mathbb R^n\to\mathbb R^n\) be a network : \(f_\theta (x) = \nabla \psi_\theta (x)\),
where \(\psi_\theta : \mathbb R^n \to \mathbb R,\) convex and differentiable (ICNN).
Then,
1. Existence of regularizer
\(\exists ~R_\theta : \mathbb R^n \to \mathbb R\) not necessarily convex : \(f_\theta(x) \in \text{prox}_{R_\theta}(x),\)
2. Computability
We can compute \(R_{\theta}(x)\) by solving a convex problem
Learned Proximals
: revisiting PnP
How do we find \(f(x) = \text{prox}_R(x)\) for the "correct" \(R(x) \propto -\log p_x(x)\)?
Learned Proximals
: revisiting PnP
Theorem [Fang, Buchanan, S.]
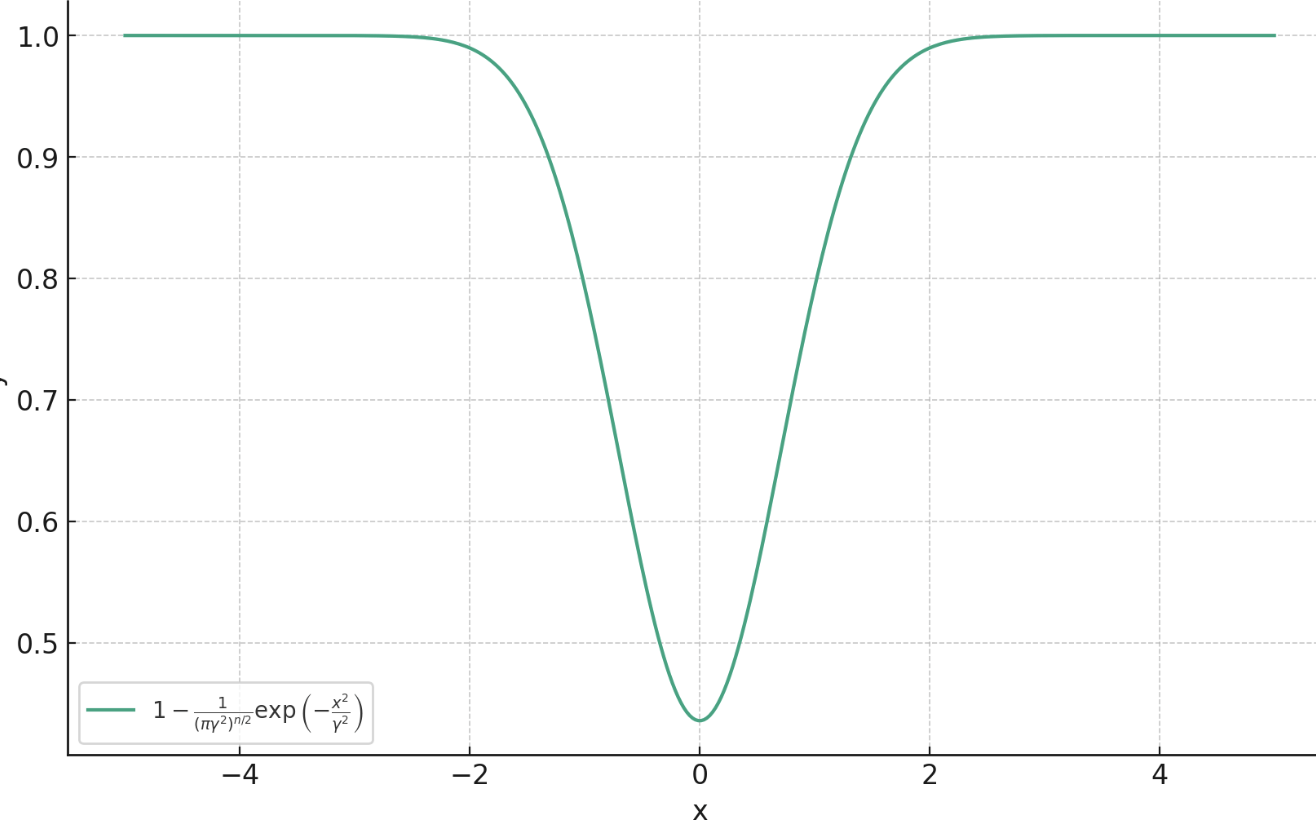
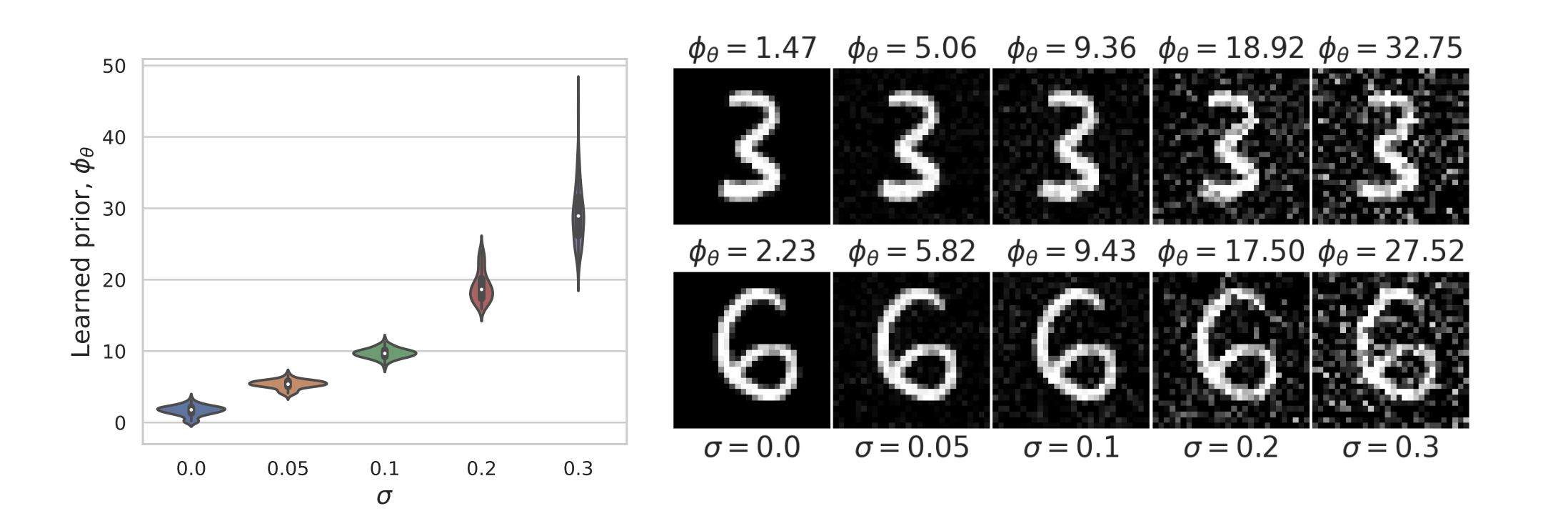
Proximal Matching Loss:\(\gamma\)
Goal: train a denoiser \(f(y)\approx x\)
Let
Then,
a.s.
Learned Proximal Networks
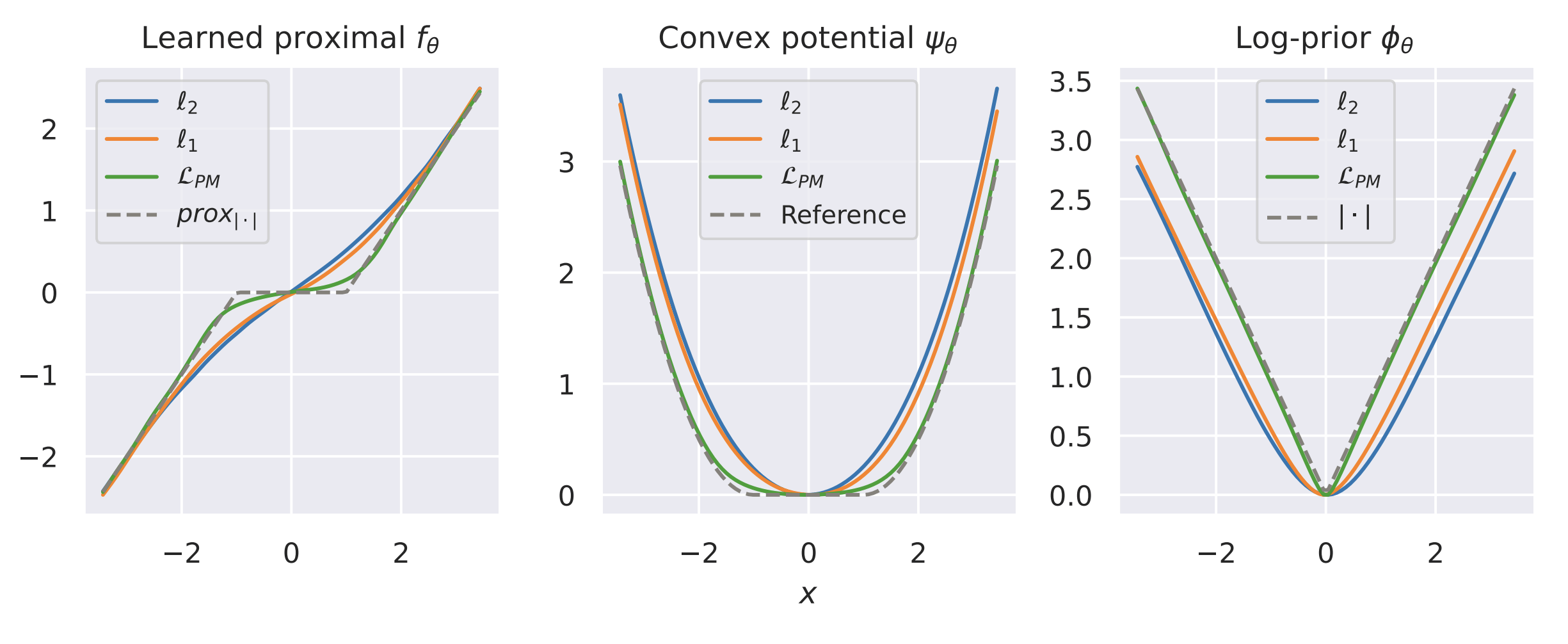


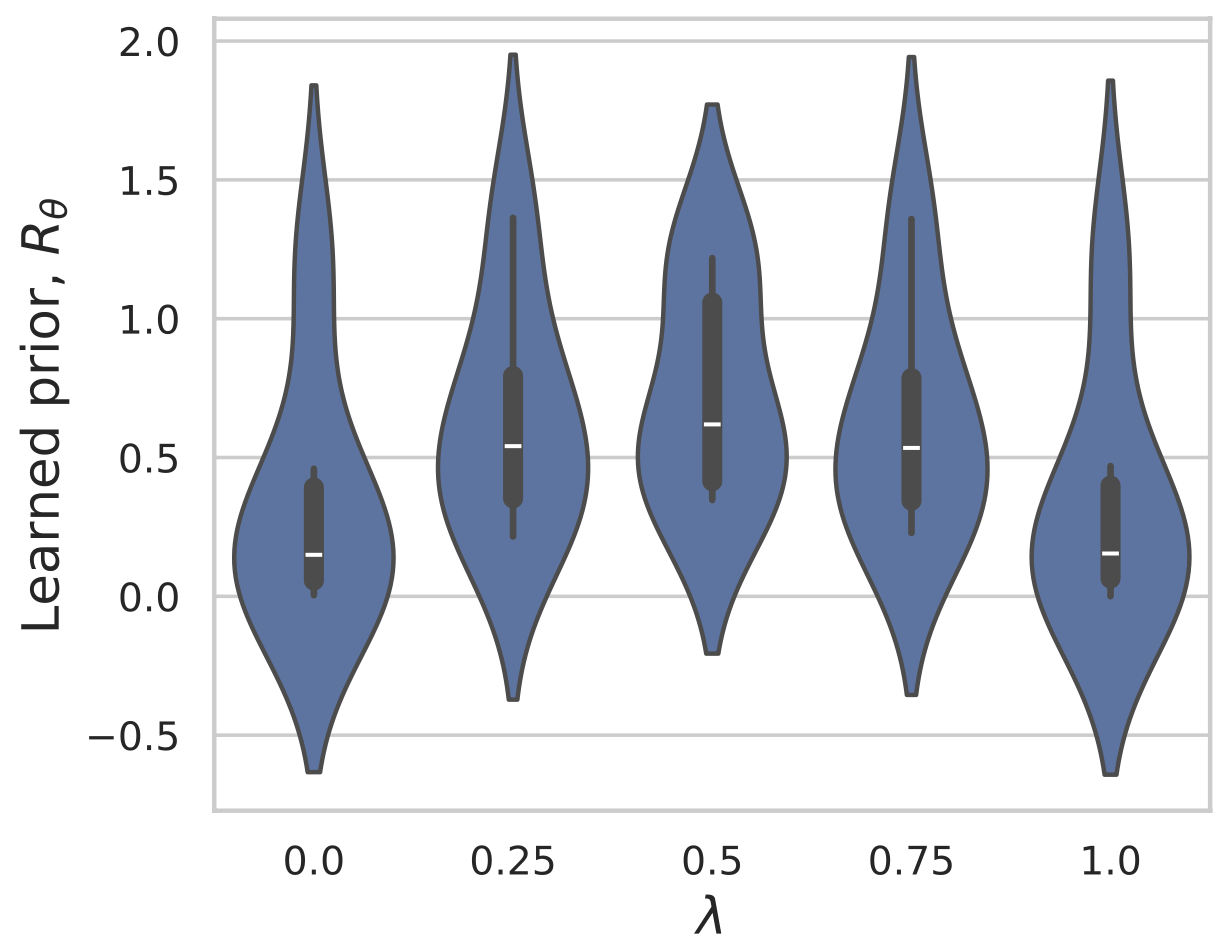
Example: recovering a prior
Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems, ICLR 2024.

Learned Proximal Networks in
Convergence guarantees
inverse problems
Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems, ICLR 2024.
Learned Proximal Networks in
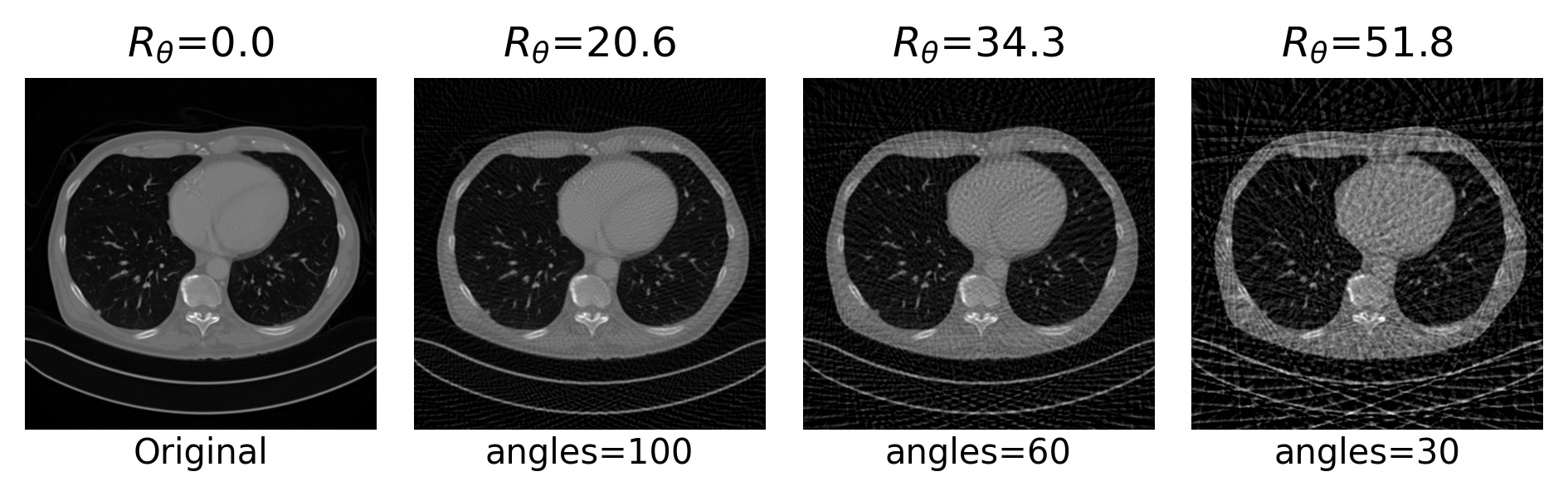
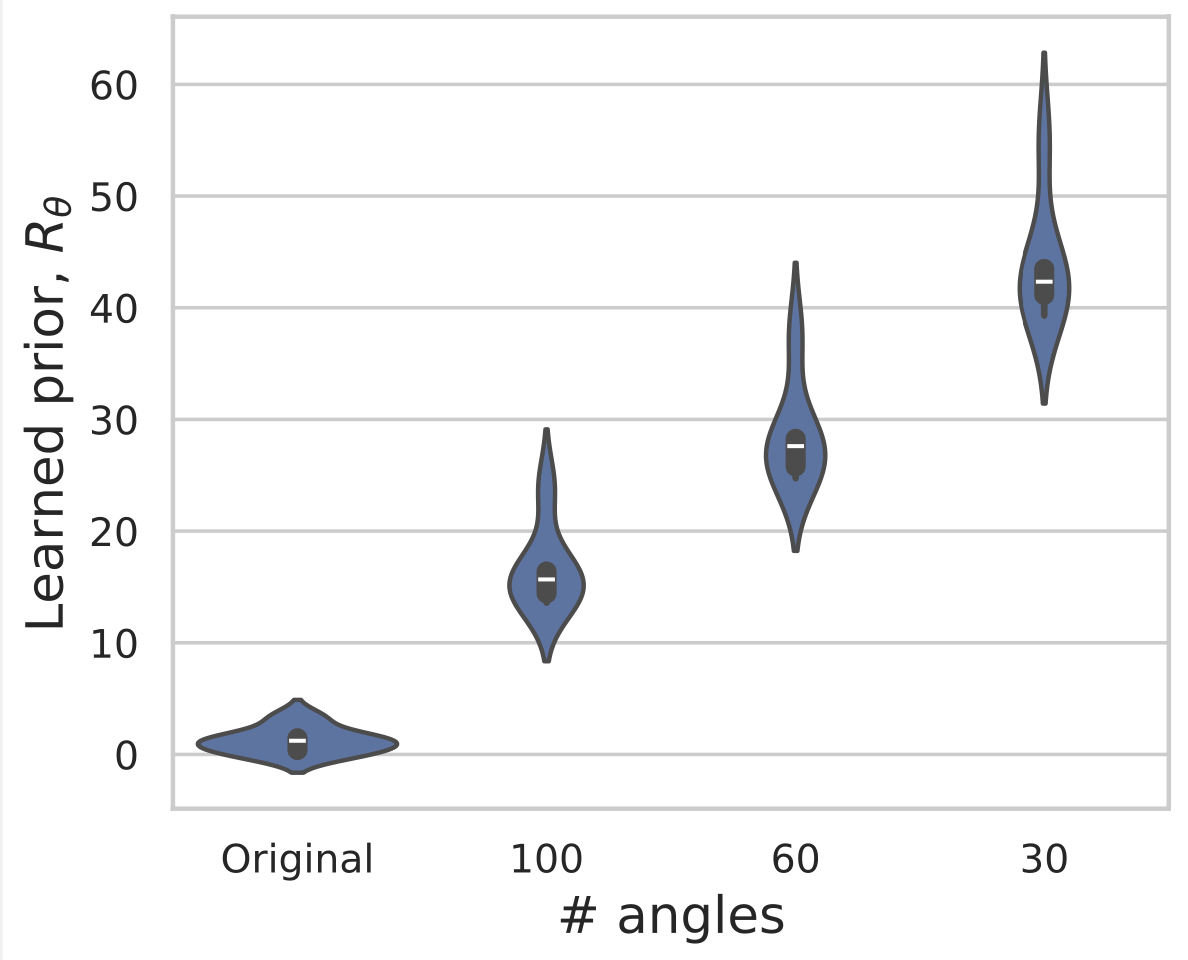
\(R_\theta(x) = 0.0\)
\(R_\theta(x) = 127.37\)
\(R_\theta(x) = 274.13\)
\(R_\theta(x) = 290.45\)
Understanding the learned model provides new insights:
inverse problems
Take-home message 1
- Learned Proximal Networks (LPNs) provide data-dependent proximal operators
- Allow characterization of the learned priors.
Learned Proximal Networks
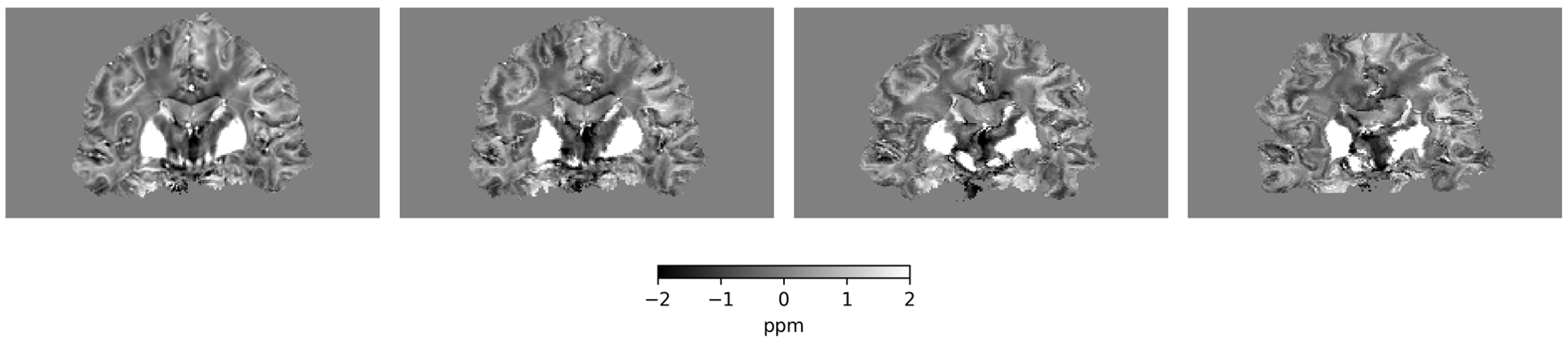
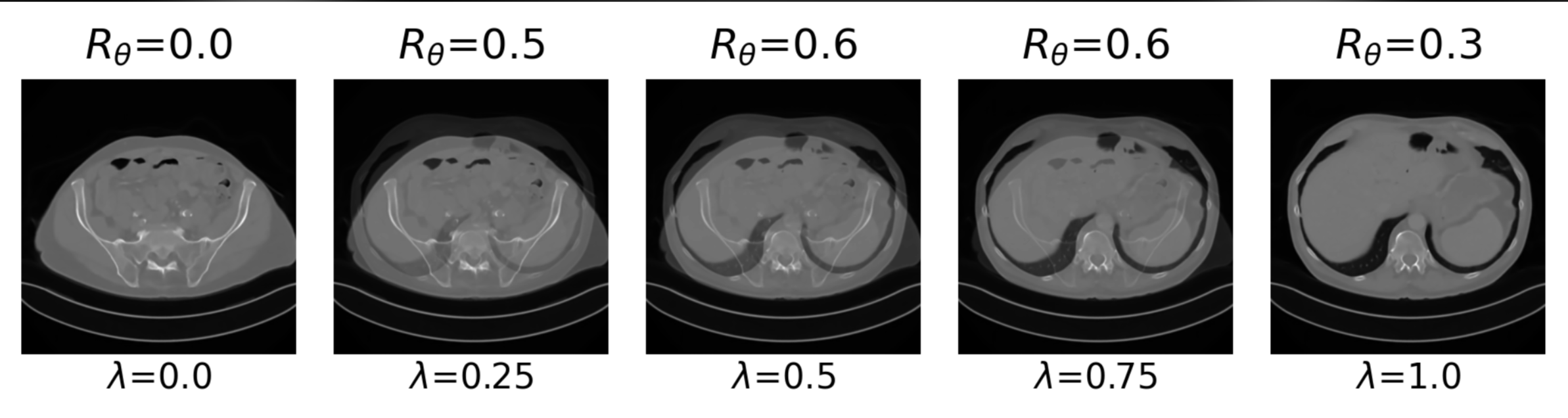
Example 2: a prior for CT
Learned Proximal Networks

Example 2: a prior for CT
Learned Proximal Networks

Example 2: a prior for CT


Learned Proximal Networks
Example 2: a prior for CT




Learned Proximal Networks
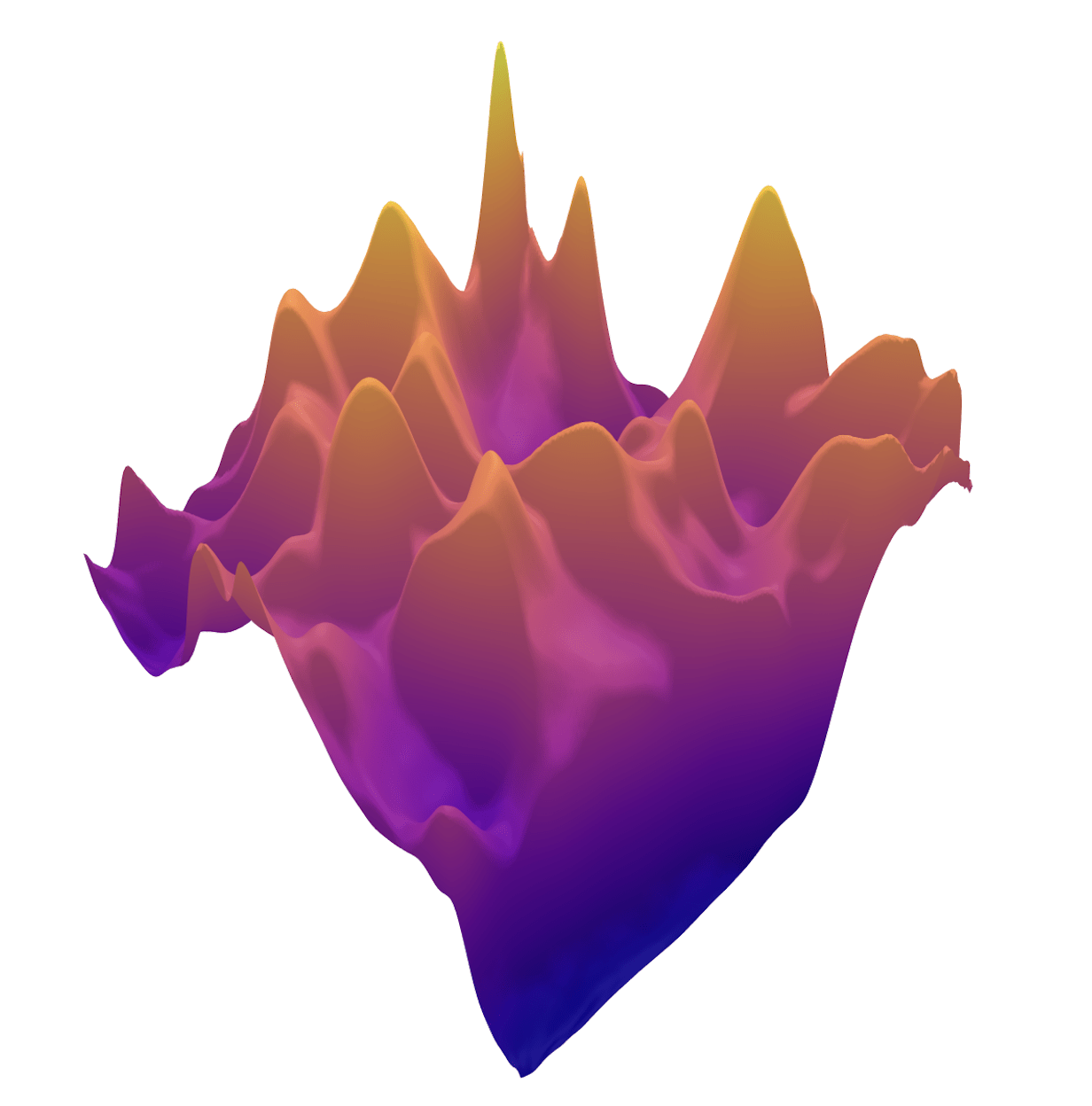

\(R(\tilde{x})\)
Example 2: priors for images












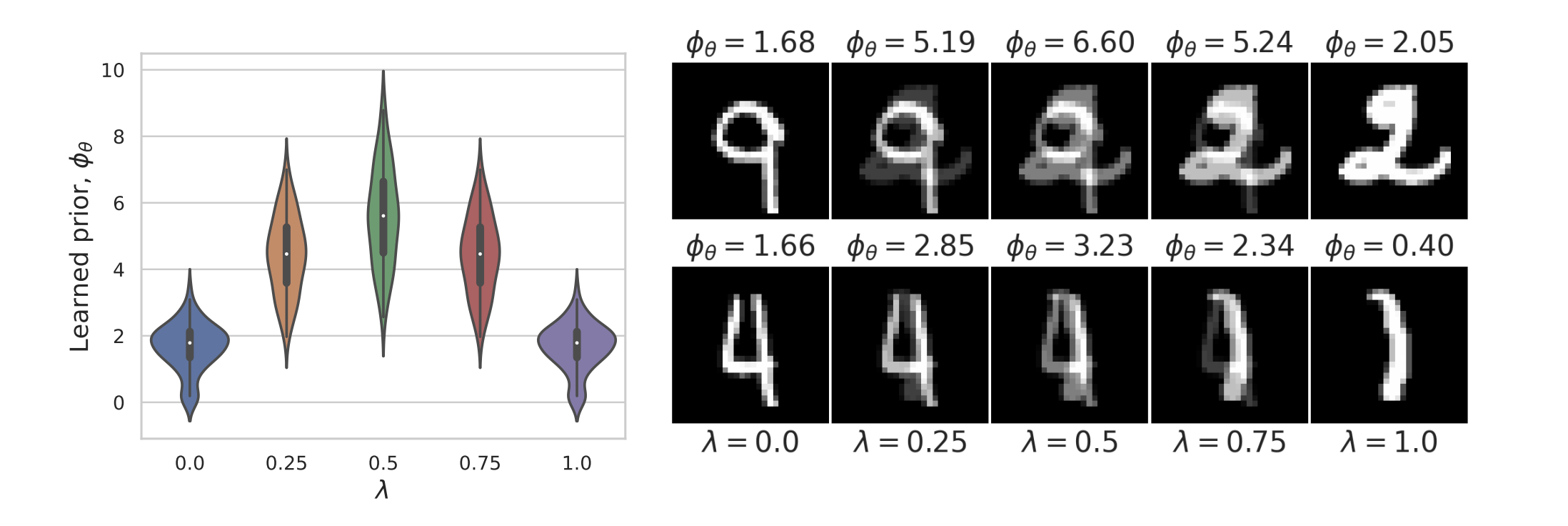













Learned Proximal Networks
Example 2: priors for images
Learned Proximal Networks
via
Convergence Guarantees
Theorem (PGD with Learned Proximal Networks)
Let \(f_\theta = \text{prox}_{\hat{R}} {\color{grey}\text{ with } \alpha>0}, \text{ and } 0<\eta<1/\sigma_{\max}(A) \) with smooth activations
(Analogous results hold for ADMM)
Learned Proximal Networks
Convergence guarantees for PnP

in a box
Denoiser
diffusion
Measurements
\[y = Ax + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2\mathbb{I})\]
\[\hat{x} = F(y) \sim \mathcal{P}_y\]
Hopefully \(\mathcal{P}_y \approx p(x \mid y)\), but not needed!







Reconstruction
Question 3)
How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)
Question 4)
How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?
Conformal guarantees for diffusion models
Lemma
Given \(m\) samples from \(\mathcal P_y\), let
\[\mathcal{I}(y)_j = \left[ Q_{y_j}\left(\frac{\lfloor(m+1)\alpha/2\rfloor}{m}\right), Q_{y_j}\left(\frac{\lceil(m+1)(1-\alpha/2)\rceil}{m}\right)\right]\]
Then \(\mathcal I(y)\) provides entriwise coverage for a new sample \(\hat x \sim \mathcal P_y\), i.e.
\[\mathbb{P}\left[\hat{x}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
\(0\)
\(1\)
low: \( l(y) \)
\(\mathcal{I}(y)\)
up: \( u(y) \)
Question 3)
How much uncertainty is there in the samples \(\hat x \sim \mathcal P_y?\)
(distribution free)
cf [Feldman, Bates, Romano, 2023]

\(y\)
lower
upper
intervals
\(|\mathcal I(y)_j|\)
Conformal guarantees for diffusion models
\(0\)
\(1\)
ground-truth is
contained
\(\mathcal{I}(y_j)\)
\(x_j\)
Conformal guarantees for diffusion models
Question 4)
How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?
Conformal guarantees for diffusion models
[Angelopoulos et al, 2022]
[Angelopoulos et al, 2022]
Risk Controlling Prediction Set
For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
[Angelopoulos et al, 2022]
Question 4)
How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?
\(0\)
\(1\)
ground-truth is
contained
\(\mathcal{I}(y_j)\)
\(x_j\)
Conformal guarantees for diffusion models
[Angelopoulos et al, 2022]
ground-truth is
contained
\(0\)
\(1\)
\(\mathcal{I}(y_j)\)
\(\lambda\)
\(x_j\)
Procedure:
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~ \hat{\text{risk}}_{(\mathcal S_{cal})} \leq \epsilon,~\forall \lambda' \geq \lambda \}\]
[Angelopoulos et al, 2022]
single \(\lambda\) for all \(\mathcal I(y_j)\)!
Risk Controlling Prediction Set
For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
[Angelopoulos et al, 2022]
Question 4)
How far will the samples \(\hat x \sim \mathcal P_y\) be from the true \(x\)?
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [l_\text{low,j} - \lambda, l_\text{up,j} + \lambda]\)
Conformal guarantees for diffusion models
\(K\)-RCPS: High-dimensional Risk Control
\[\tilde{{\lambda}}_K = \underset{\lambda \in \mathbb R^K}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad \text{s.t. }\quad \mathcal I_{\lambda_j}(y) : \text{RCPS}\]
scalar \(\lambda \in \mathbb{R}\)
vector \(\bm{\lambda} \in \mathbb{R}^d\)
\(\mathcal{I}_{\lambda}(y)_j = [\text{low}_j - \lambda, \text{up}_j + \lambda]\)
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low}_j - \lambda_j, \text{up}_j + \lambda_j]\)
\(\rightarrow\)
\(\rightarrow\)
Procedure:
1. Find anchor point
\[\tilde{\bm{\lambda}}_K = \underset{\bm{\lambda}}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad\text{s.t.}~~~\hat{\text{risk}}^+(\bm{\lambda})_{(S_{opt})} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\hat{\text{risk}}_{S_{cal}}^+(\tilde{\bm{\lambda}}_K + \beta'\bf{1}) \leq \epsilon,~\forall~ \beta' \geq \beta\}\]
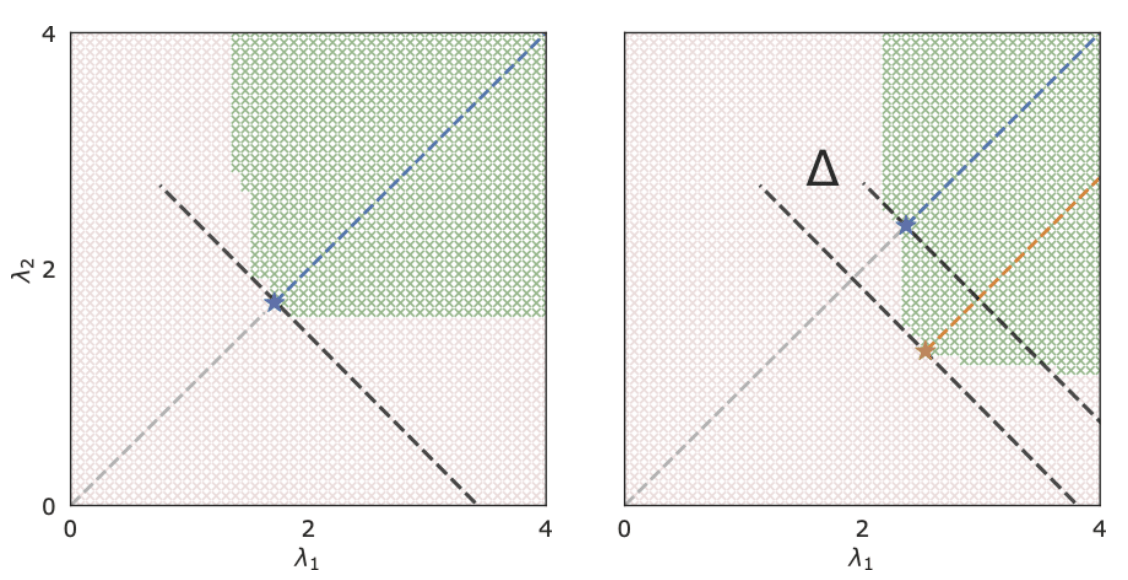
\(\tilde{\bm{\lambda}}_K\)
Conformal guarantees for diffusion models
\(K\)-RCPS: High-dimensional Risk Control
\[\tilde{{\lambda}}_K = \underset{\lambda \in \mathbb R^K}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad \text{s.t. }\quad \mathcal I_{\lambda_j}(y) : \text{RCPS}\]
scalar \(\lambda \in \mathbb{R}\)
vector \(\bm{\lambda} \in \mathbb{R}^d\)
\(\rightarrow\)
\(\rightarrow\)
Procedure:
1. Find anchor point
\[\tilde{\bm{\lambda}}_K = \underset{\bm{\lambda}}{\arg\min}~\sum_{k \in [K]}\lambda_k~\quad\text{s.t.}~~~\hat{\text{risk}}^+(\bm{\lambda})_{(S_{opt})} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\hat{\text{risk}}_{S_{cal}}^+(\tilde{\bm{\lambda}}_K + \beta'\bf{1}) \leq \epsilon,~\forall~ \beta' \geq \beta\}\]

\(\hat{R}^{\gamma}(\bm{\lambda}_{S_{opt}})\leq \epsilon\)
Guarantee: \(\mathcal{I}_{\bm{\lambda}_K,\hat{\beta}}(y)_j \) are \((\epsilon,\delta)\)-RCPS
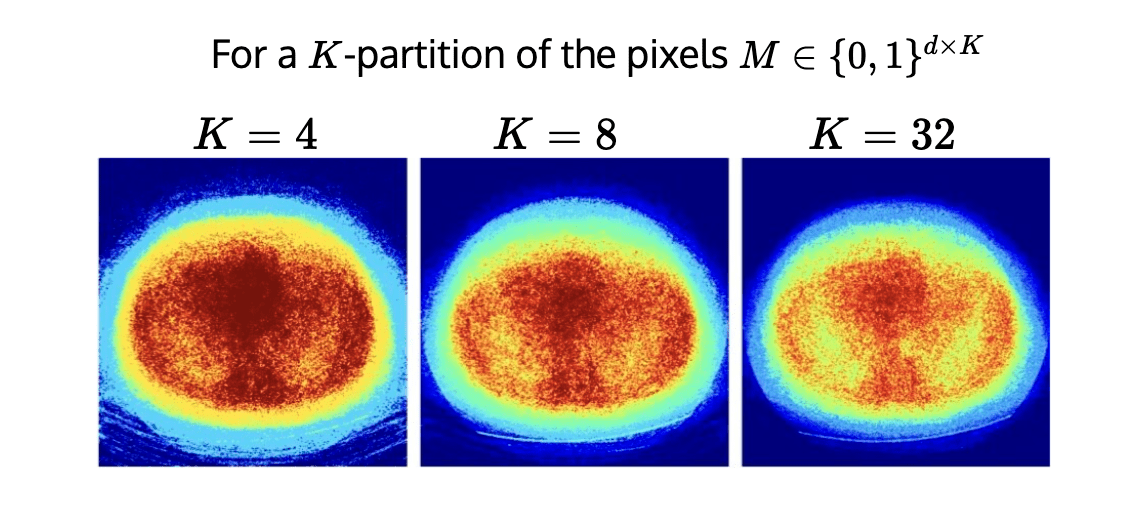
\(\tilde{\bm{\lambda}}_K\)
\(\mathcal{I}_{\lambda}(y)_j = [\text{low}_j - \lambda, \text{up}_j + \lambda]\)
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low}_j - \lambda_j, \text{up}_j + \lambda_j]\)

\(\hat{\lambda}_K\)
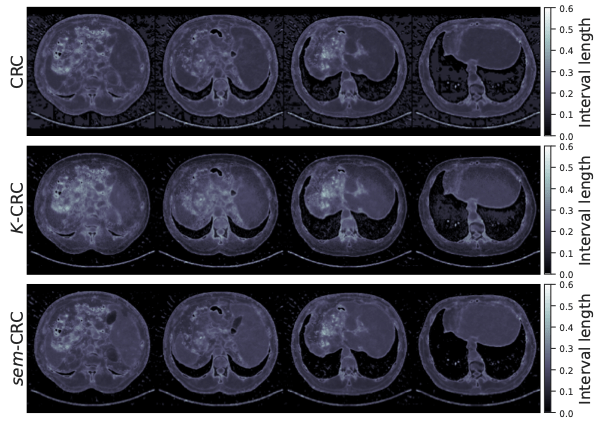
conformalized uncertainty maps
\(K=4\)
\(K=8\)

\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]

Conformal guarantees for diffusion models
c.f. [Kiyani et al, 2024]
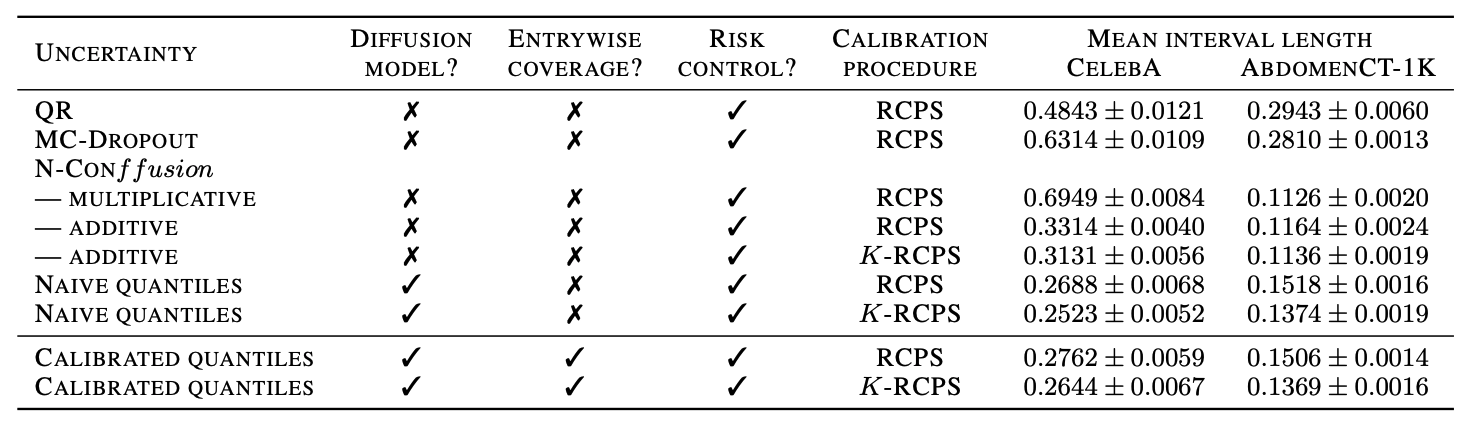
Teneggi, Tivnan, Stayman, S. How to trust your diffusion model: A convex optimization approach to conformal risk control. ICML 2023
Medtronic 2025
By Jeremias Sulam
Medtronic 2025
- 86



