New strongly regular graphs from real line packings
John Jasper
Air Force Institute of Technology
AMS Spring Sectional Meeting

The views expressed in this talk are those of the speaker and do not reflect the official policy
or position of the United States Air Force, Department of Defense, or the U.S. Government.
https://slides.com/johnjasper/amscincy/
Equiangular Tight Frames (ETF)
Definition. Let \[\Phi = \big[\varphi_{1}\ \ \varphi_{2}\ \ \cdots\ \ \varphi_{N}\big]\in \mathbb{F}^{d\times N},\]
be a rank \(d\) matrix where each column \(\varphi_{n}\) is unit norm
\[\|\varphi_{n} \|^{2}=1.\]
1) (Tightness) \(\exists\,A>0\) such that \((\Phi^{\ast}\Phi)^{2} = A\Phi^{\ast}\Phi\).
2) (Equiangular) \(\exists\,B>0\) such that \(|\frac{1}{B}\varphi_{m}^{\ast}\varphi_{n}^{}|=1\) for \(m\neq n\).
If both 1) and 2) hold, then \(\{\varphi_{n}\}_{n=1}^{N}\) is an ETF(\(d,N)\).
\[\Phi^{\ast}\Phi = \left[\begin{array}{cccc} 1 & \varphi_{1}^{\ast}\varphi_{2} & \cdots & \varphi_{1}^{\ast}\varphi_{N}\\[1ex] \varphi_{2}^{\ast}\varphi_{1} & 1 & \cdots & \varphi_{2}^{\ast}\varphi_{N}\\[1ex] \vdots & \vdots & \ddots & \vdots\\[1ex] \varphi_{N}^{\ast}\varphi_{1} & \varphi_{N}^{\ast}\varphi_{2} & \cdots & 1\end{array}\right]\]
\(1\)'s down the diagonal
1) \(\Phi^{\ast}\Phi \propto\) projection
2) \(|\varphi_{m}^{\ast}\varphi_{n}^{}|\) constant
Examples of equiangular tight frames
Example 2. Consider the (multiple of a) unitary matrix
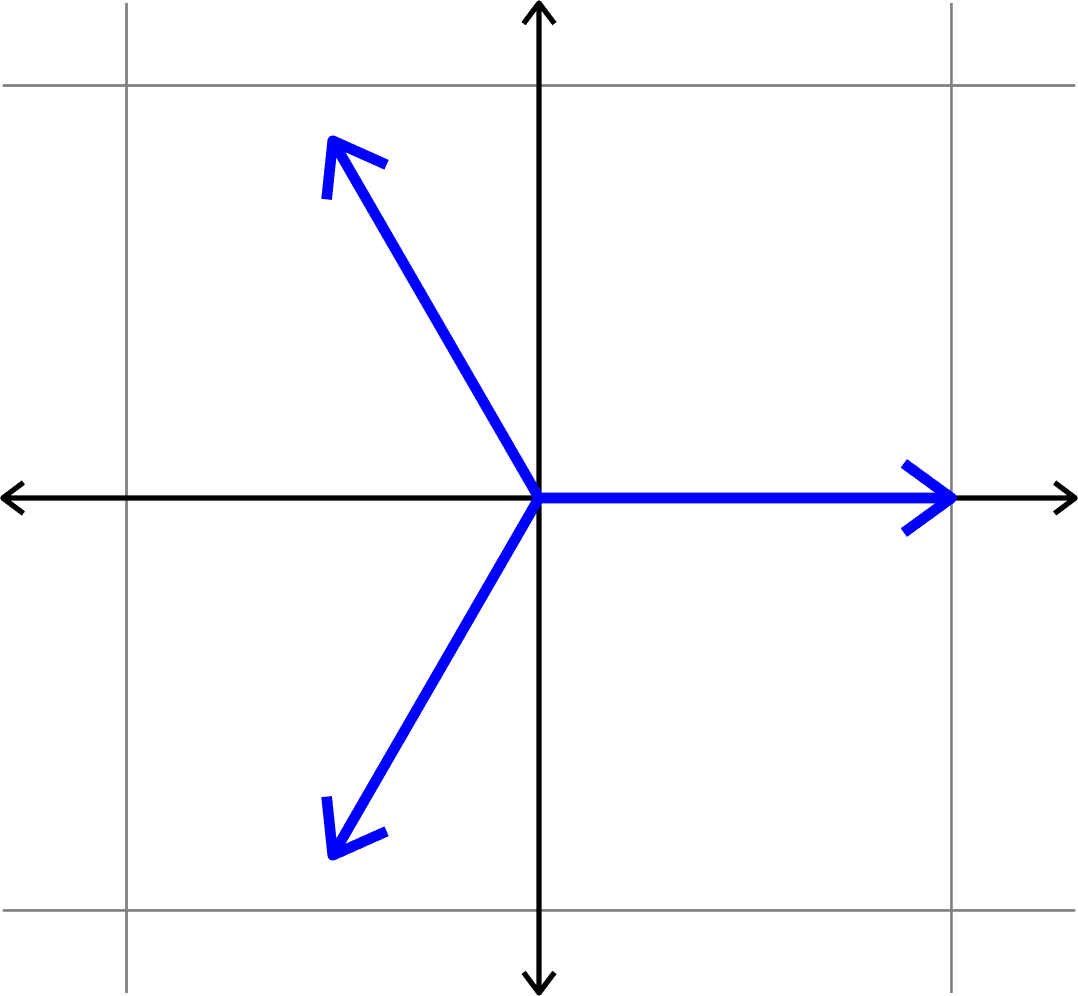
Example 1. Consider the (multiple of a) unitary matrix
\[\left[\begin{array}{rrrr}1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1\end{array}\right]\]
\[\left[\begin{array}{rrrr} 1 & 1 & 1\\ \sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
\[\left[\begin{array}{rrrr}\sqrt{2} & -\sqrt{\frac{1}{2}} & -\sqrt{\frac{1}{2}}\\ 0 & \sqrt{\frac{3}{2}} & -\sqrt{\frac{3}{2}}\end{array}\right]\]
Examples of equiangular tight frames
Example 3.
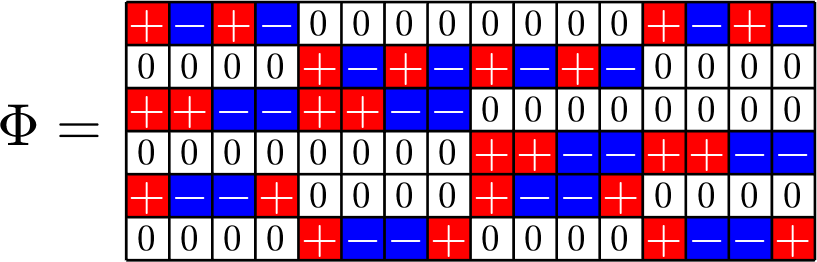
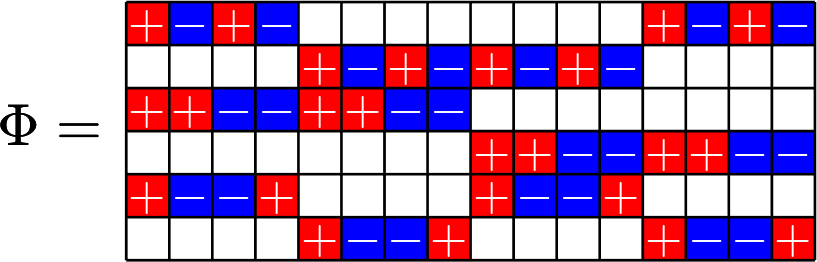

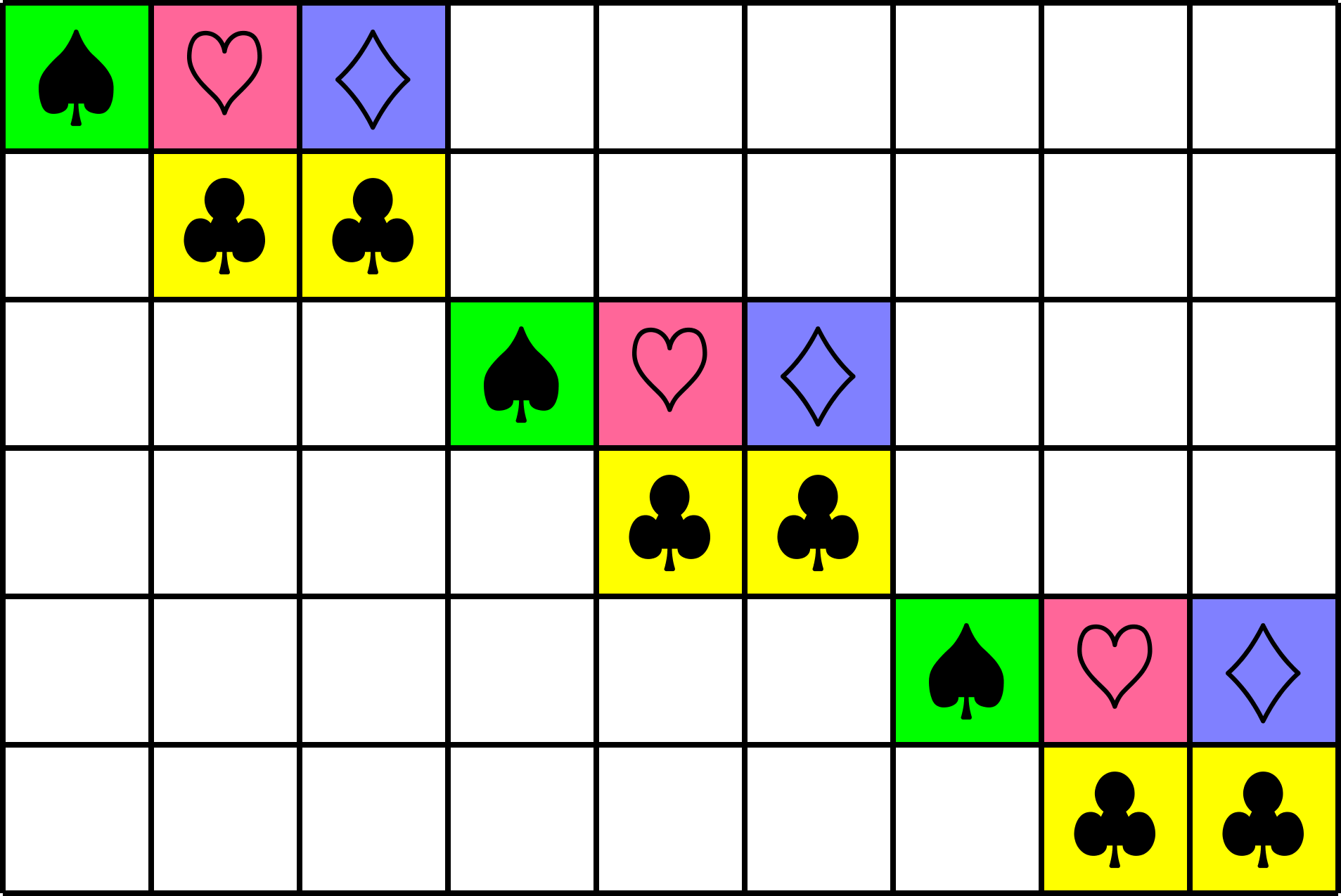
Steiner Systems
Definition. A \((2,k,v)\)-Steiner system \(\{0,1\}\)-matrix \(X\) with the following properties:
- Each row of \(X\) has exactly \(k\) ones.
- Each column of \(X\) has exactly \(r=\frac{v-1}{k-1}\) ones.
- The dot product of any distinct pair of columns is one.
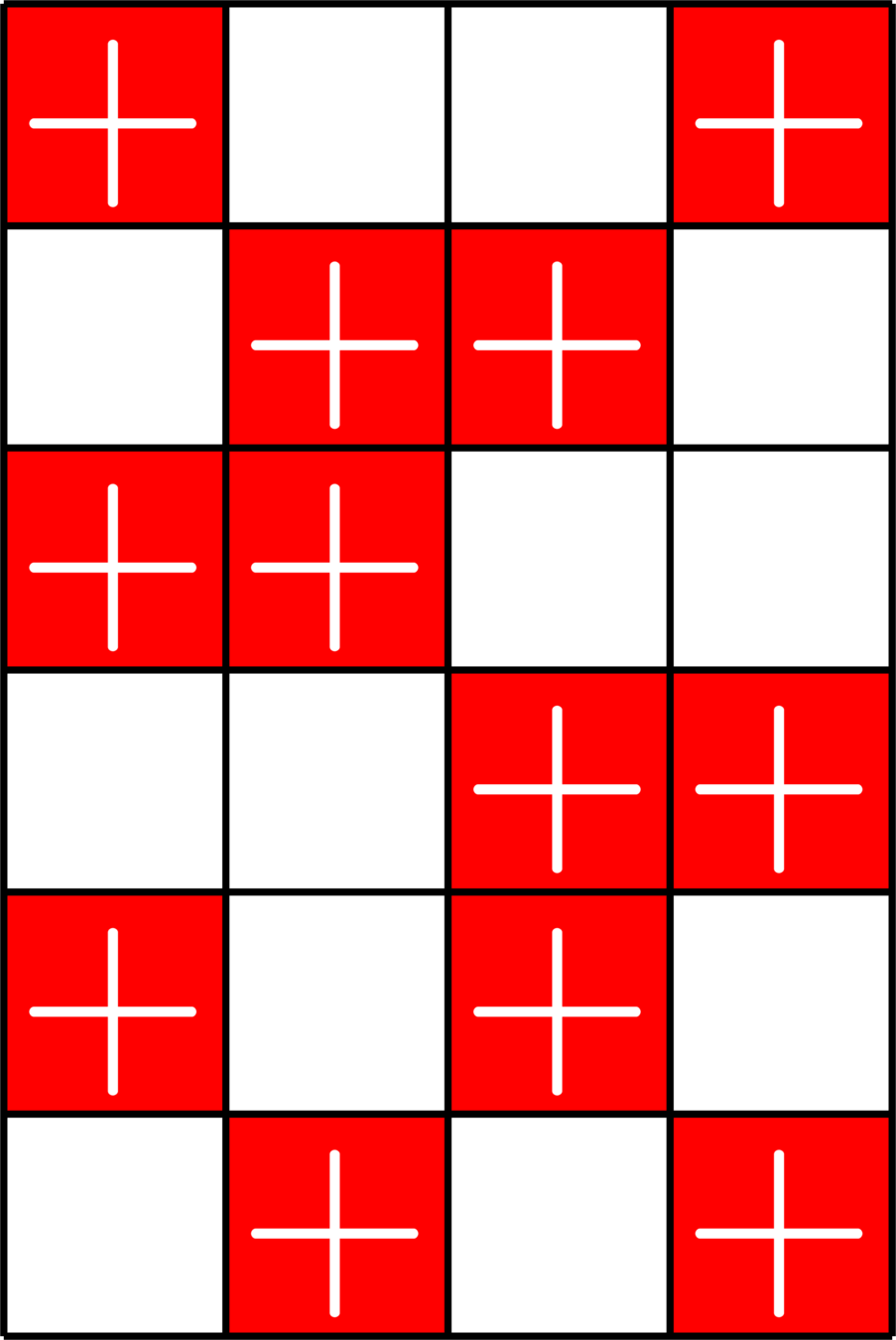
Example. The matrix
\(X = \)
is a \((2,2,4)\)-Steiner system.

The Star Product

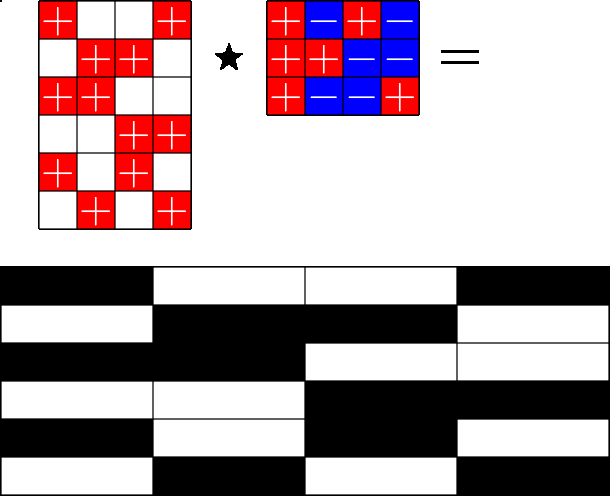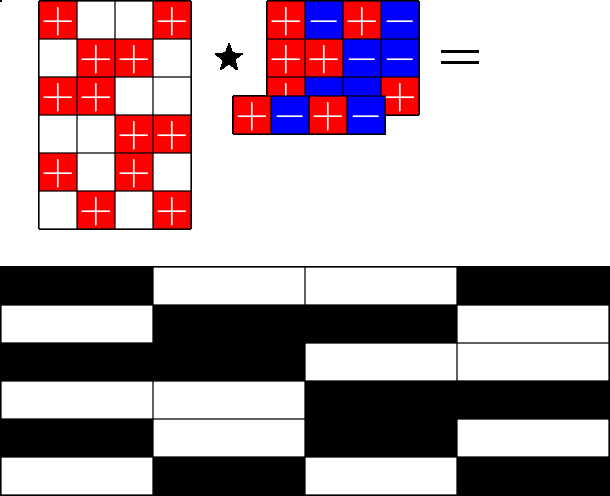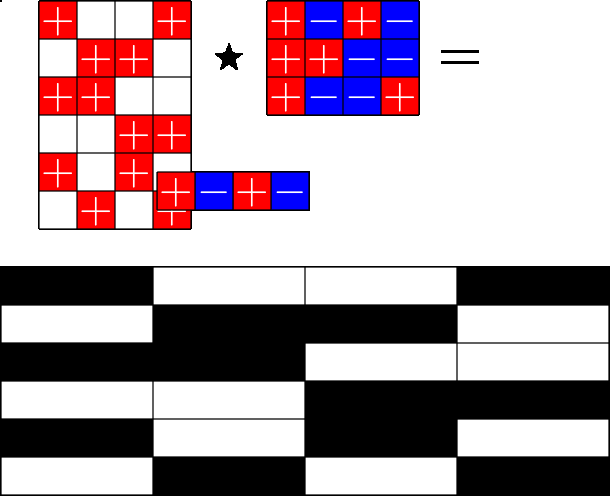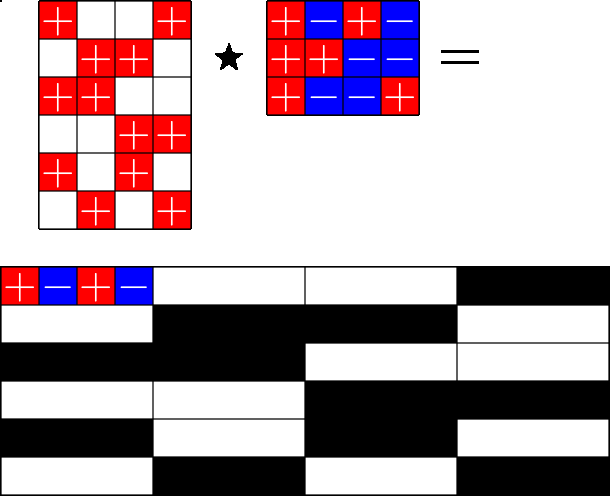
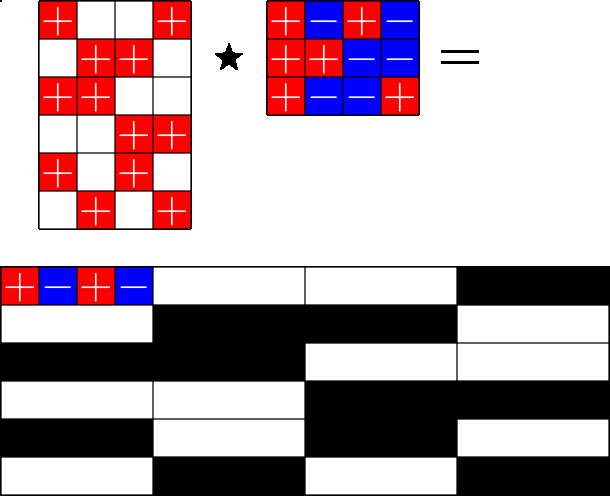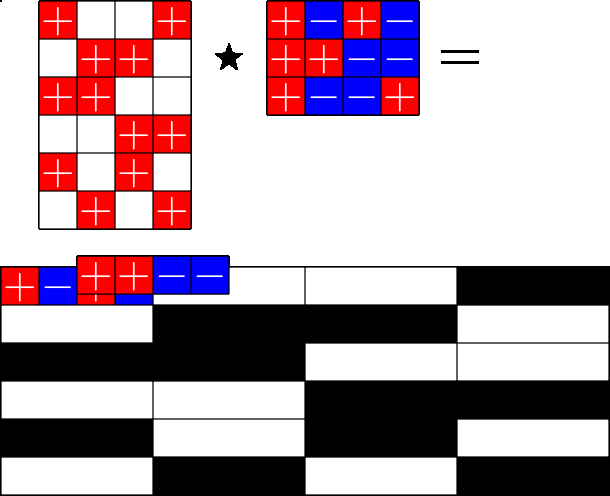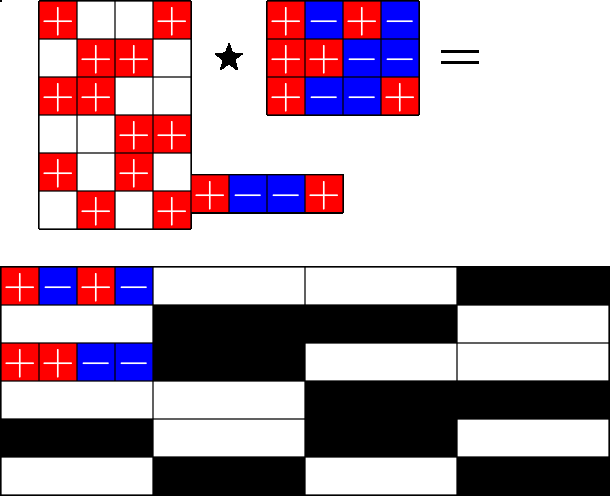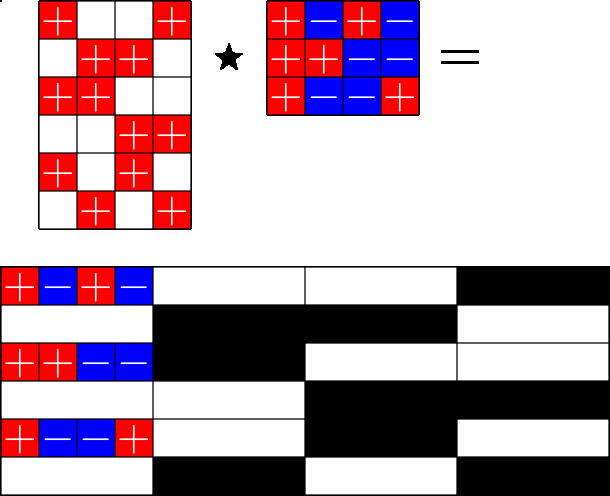
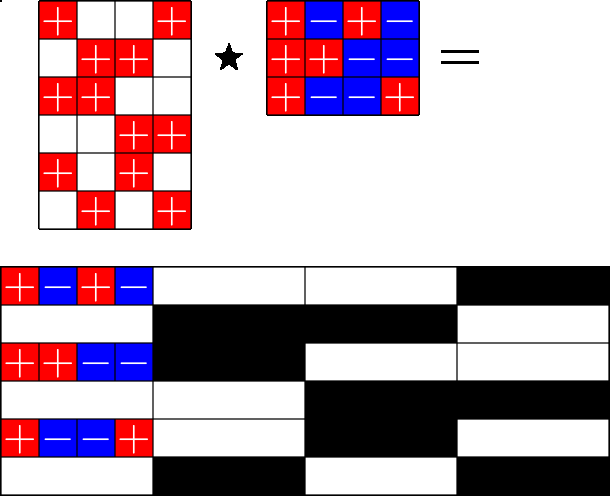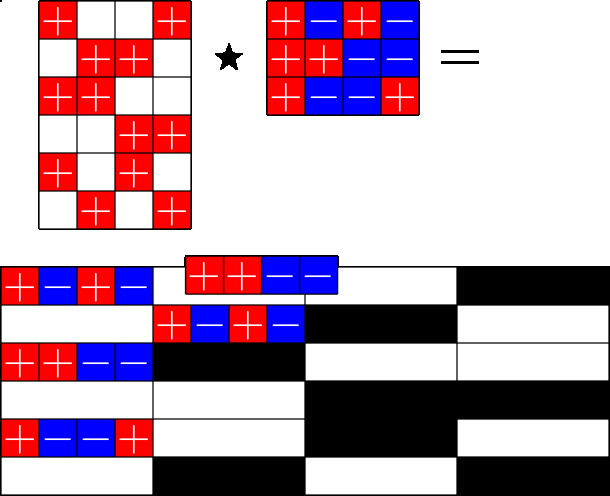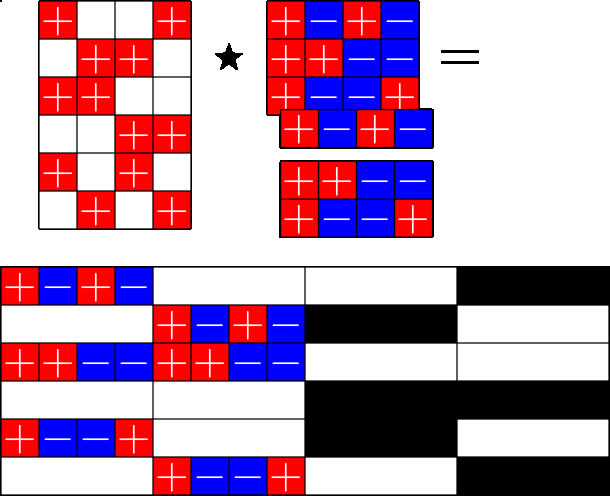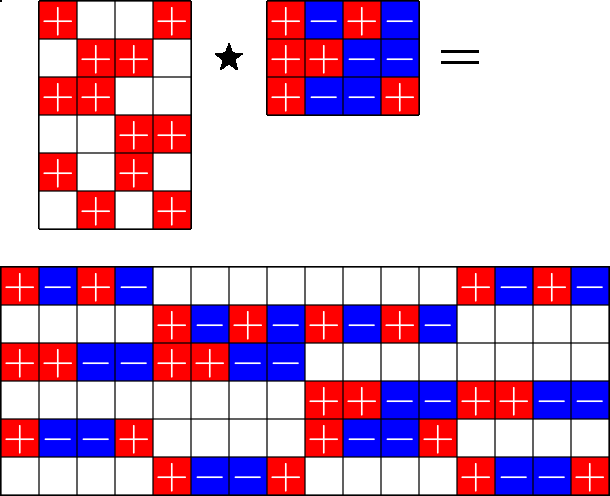
More Steiner ETFs


\(=\)
Take a Steiner system with \(r\) ones per column
and an \(r\times (r+1)\) ETF with unimodular entries
The Star product is a "Steiner" ETF
Gram matrix of ETF:
Adjacency matrix of graph:
Graphs from ETFs
- Every vertex has 9 neighbors
- Adjacent vertices have 4 common neighbors
- Non-adjacent vertices have 6 common neighbors

Replace diagonal 1's with 0's
Replace -1's with 1's
Zero out the diagonal





Mult. by \(-1\)
Strongly Regular Graphs
Definition. A simple graph on \(n\) vertices is called strongly regular if there exist nonnegative integers \(k,\lambda,\mu\) such that
- Every vertex has \(k\) neighbors.
- Every pair of adjacent vertices has \(\lambda\) common neighbors.
- Every pair of nonadjacent vertices has \(\mu\) common neighbors.
Such a graph is called an SRG\((n,k,\lambda,\mu)\).
Equivalently, if \(G\) is the adjacency matrix, then
\[G^{2} = k I + \lambda G + \mu(J-I-G)\quad\text{(where \(J\) is the all-ones matrix.)}\]
If \(\Phi\) is an ETF, then \(\Phi^{\ast}\Phi\) also satisfies a "quadratic relation":
\[(\Phi^{\ast}\Phi)^{2} = A\Phi^{\ast}\Phi.\]
But it need not have the same number of \(-1\)'s in each row!
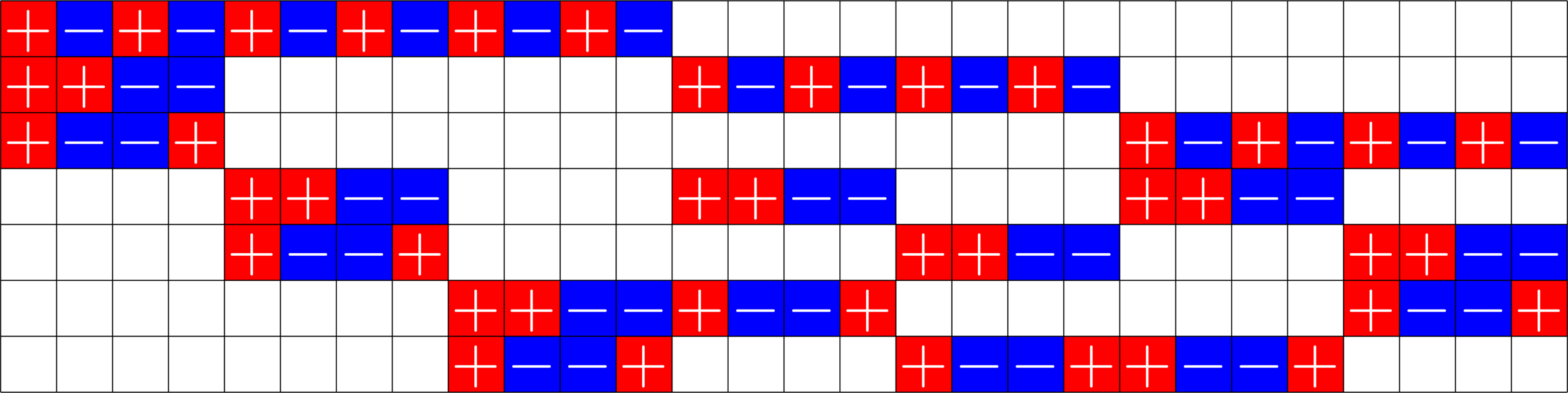
Real ETFs and Graphs
\(\Phi=\)
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
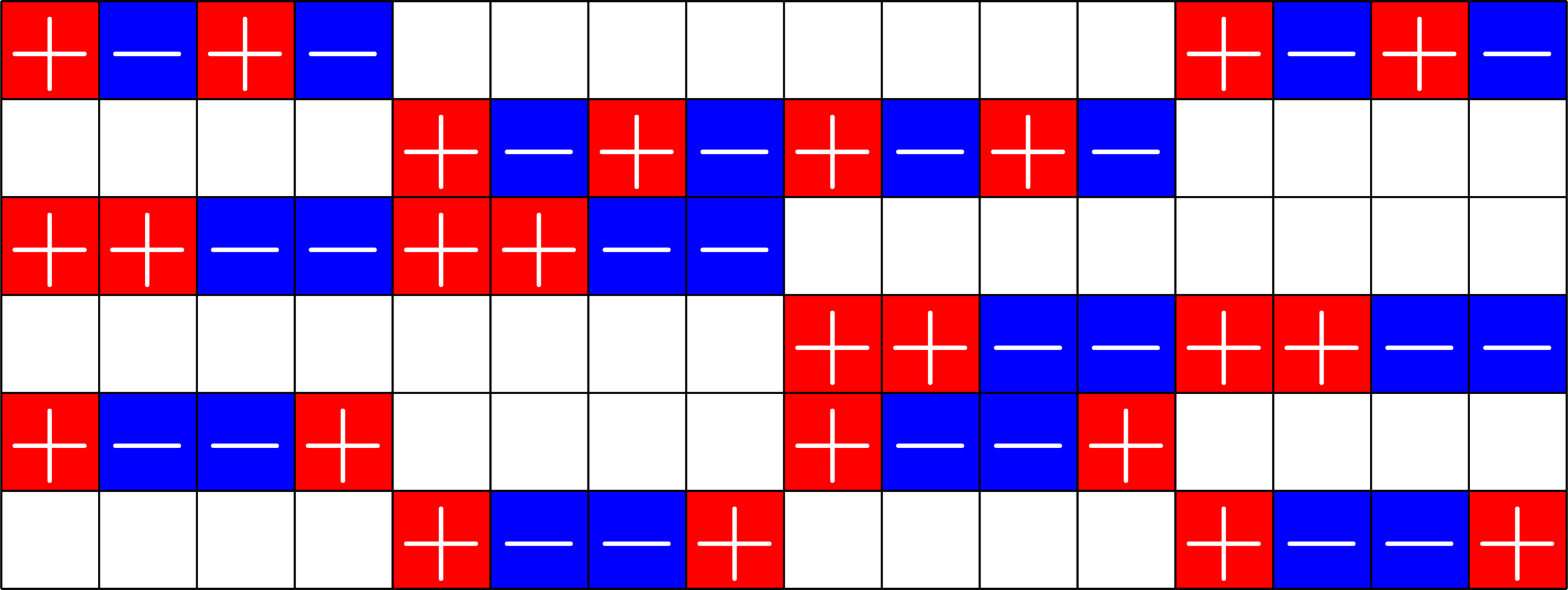
Real ETFs and Graphs
\(\Phi^{\top}\Phi=\)
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
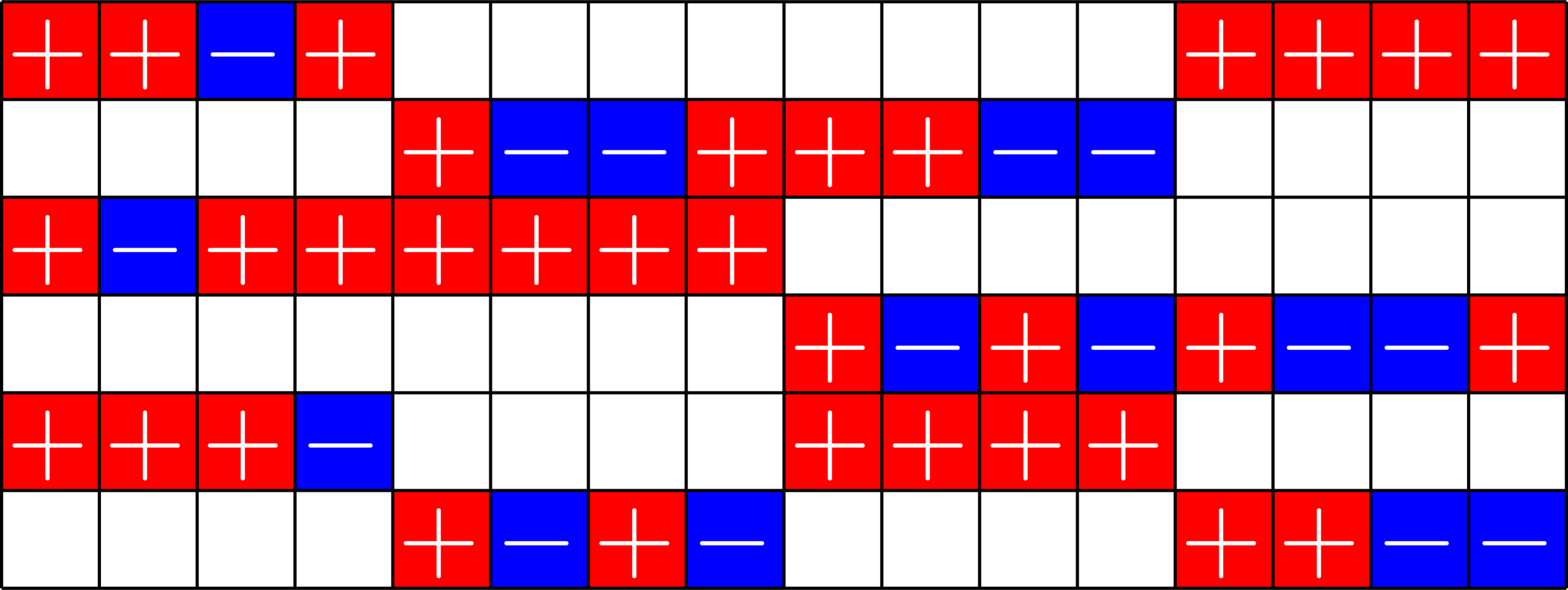
Real ETFs and Graphs
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
- Remove the first row and column and zero out the diagonal
- This is the Seidel adjacency matrix of a strongly regular graph

Real ETFs and Graphs
- Given a real ETF \(\Phi\)
- Normalize so that all dot products with the first vector are positive.
- Look at the gram matrix \(\Phi^{\top}\Phi\)
- Remove the first row and column and zero out the diagonal
- This is the Seidel adjacency matrix of a strongly regular graph


Real ETFs and Graphs
However, if
then the associated graph is already regular, and thus strongly regular. No normalization step required!
\(\mathbf{1}^{\top}\) is an eigenvector of \(\Phi^{\top}\Phi\).
- \(\mathbf{1} := [1\ \ 1\ \ \cdots\ \ 1]\) is row space of \(\Phi\), or
- \(\mathbf{1}^{\top}\in\ker\Phi\)
}
\(\Leftrightarrow\)
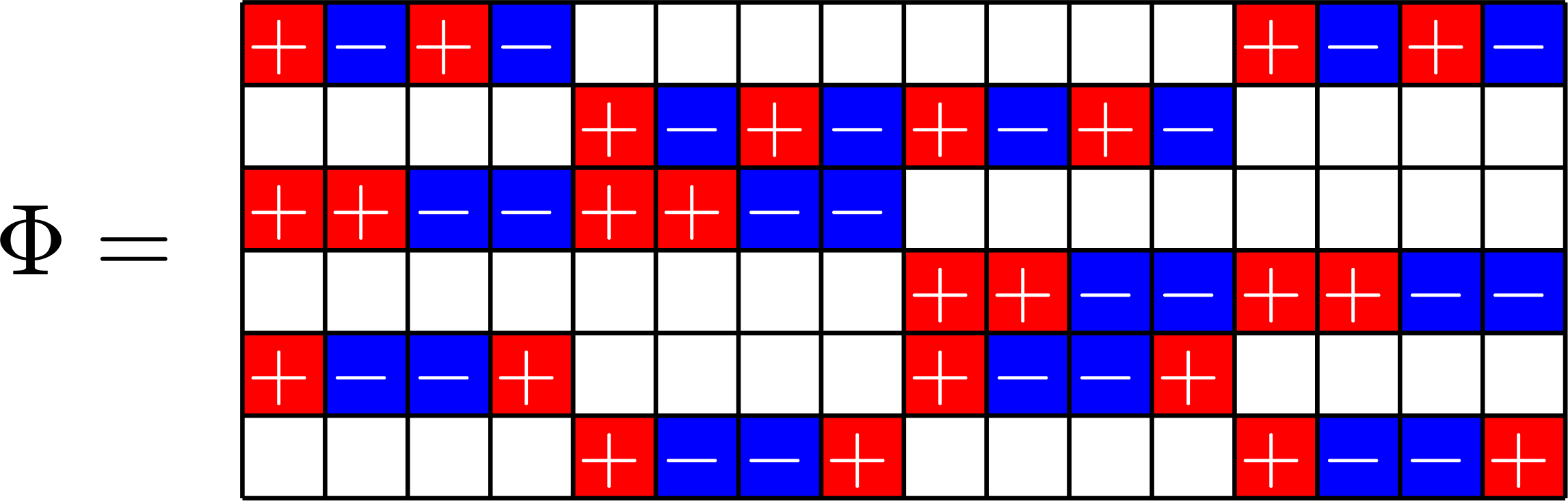
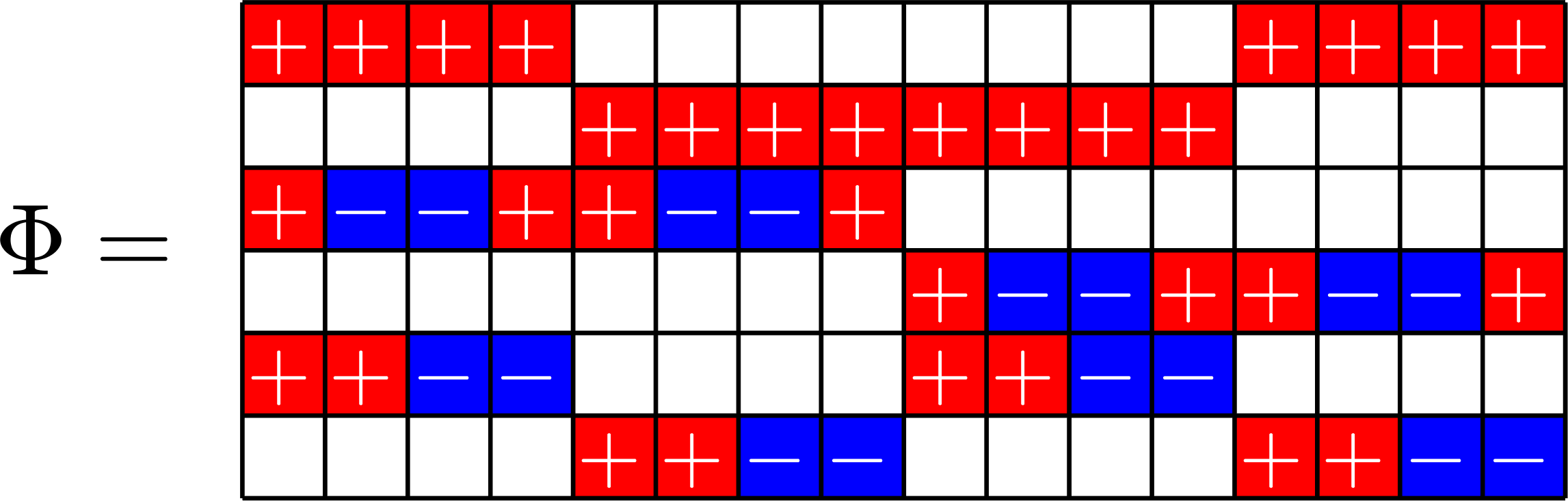
\(\mathbf{1}\) in row space
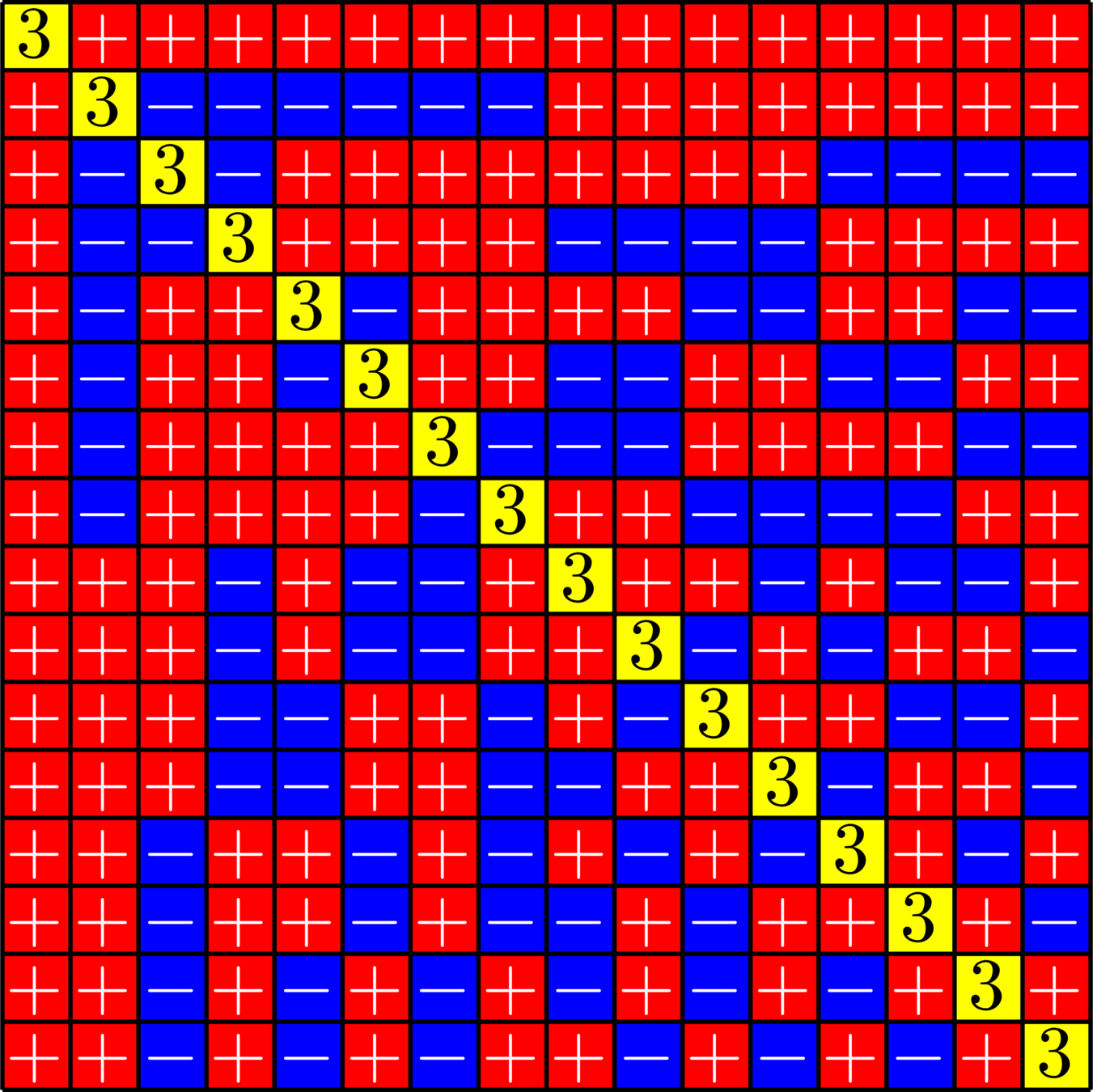
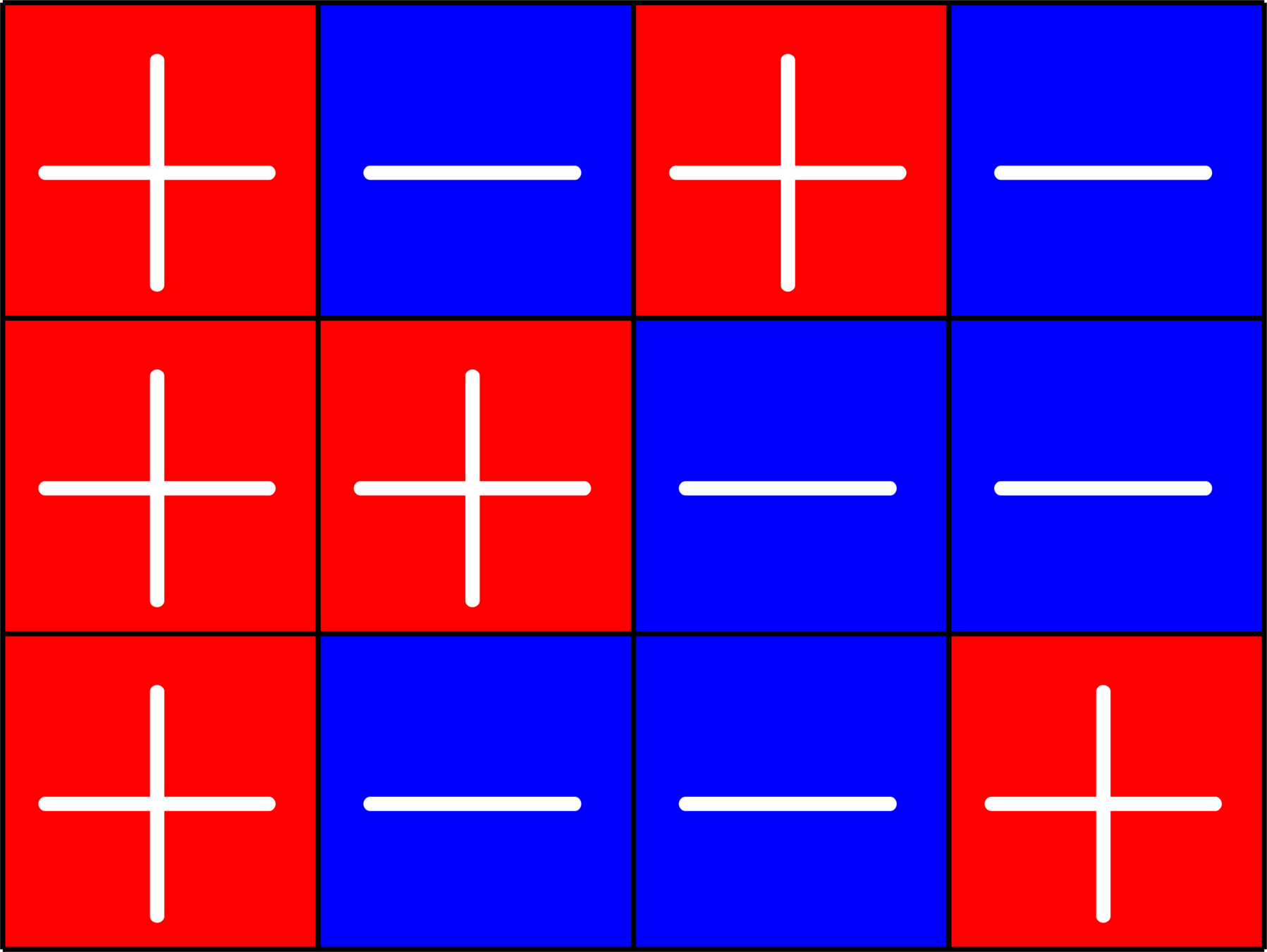
SRG\((16,5,0,2)\)
\(\mathbf{1}^{\top}\in\ker\Phi\)
SRG\((16,9,4,6)\)
Example.
Theorem [Fickus, J, Mixon,Peterson,Watson '18] . If \(\Phi\) is a \(d\times N\) real ETF, and there exists a \(\pm1\) vector which is an eigenvector of \(\Phi^{\top}\Phi\), then there exists a strongly regular graph on \(N\) vertices.
Goal: For known ETFs, find a \(\pm 1\) vector in the kernel or the row space.
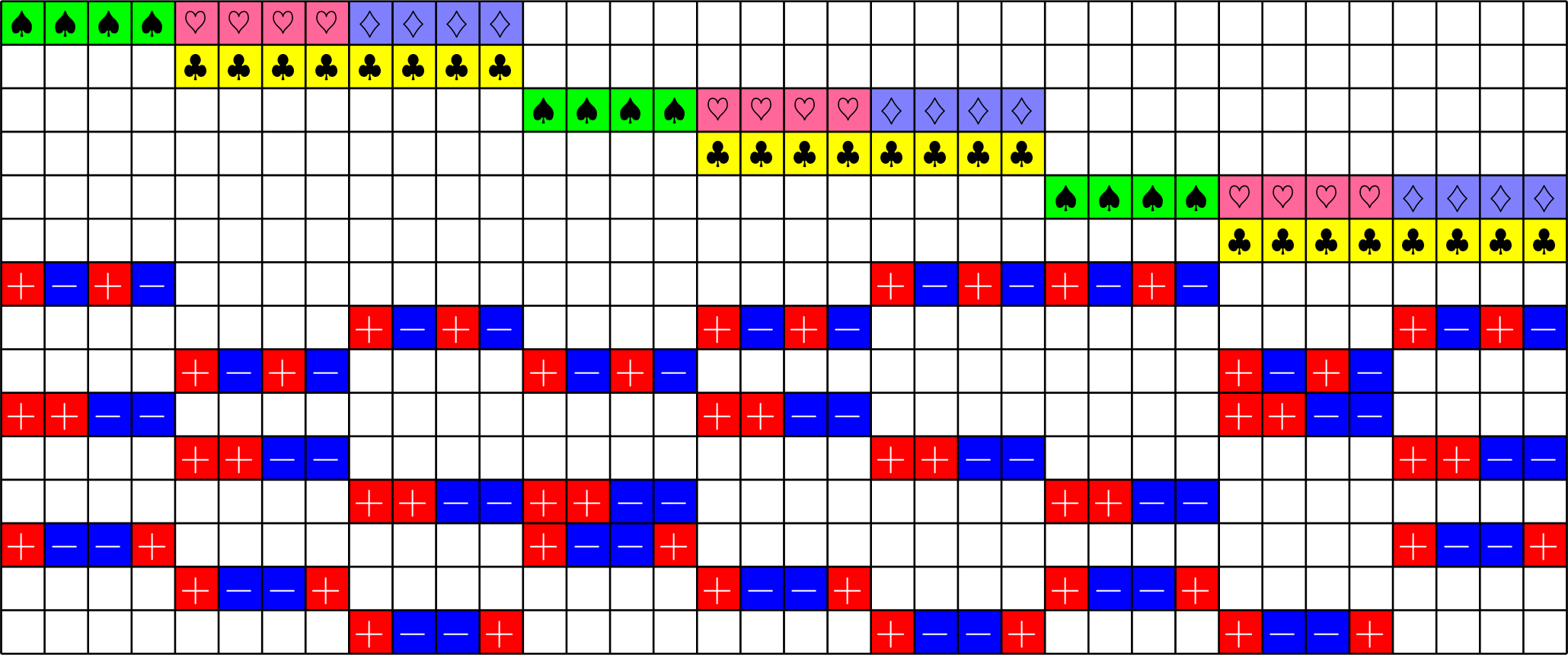
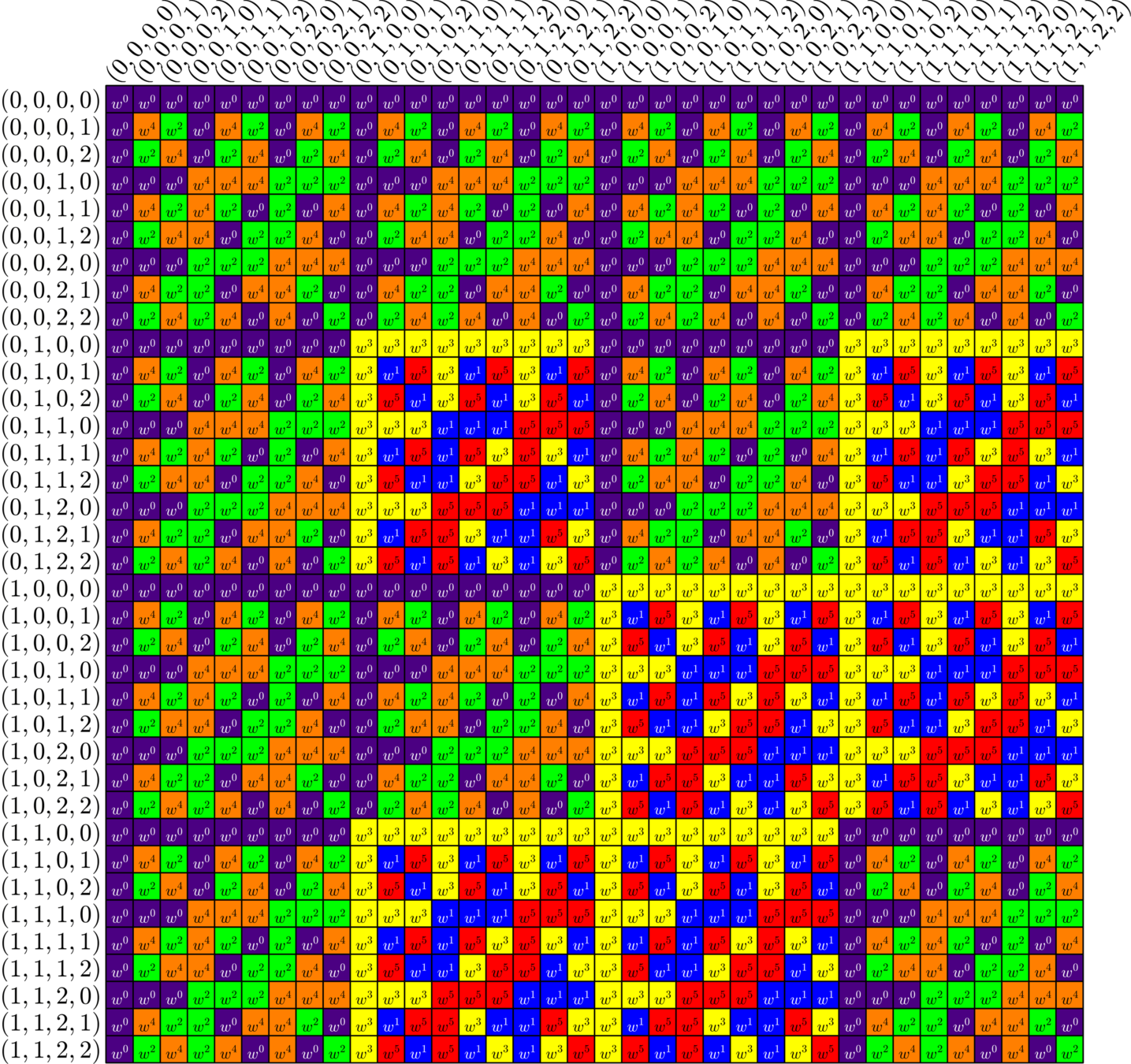
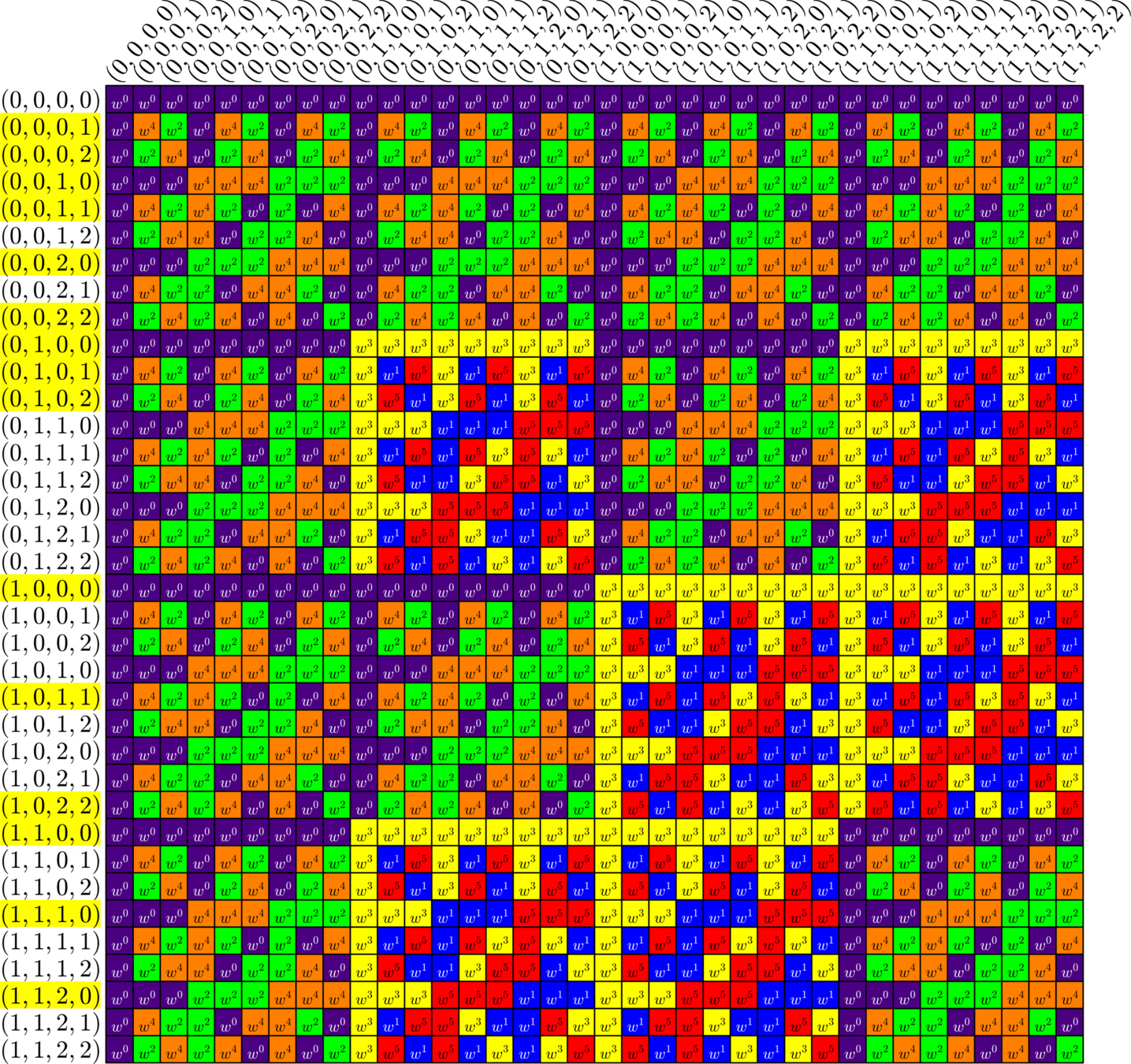
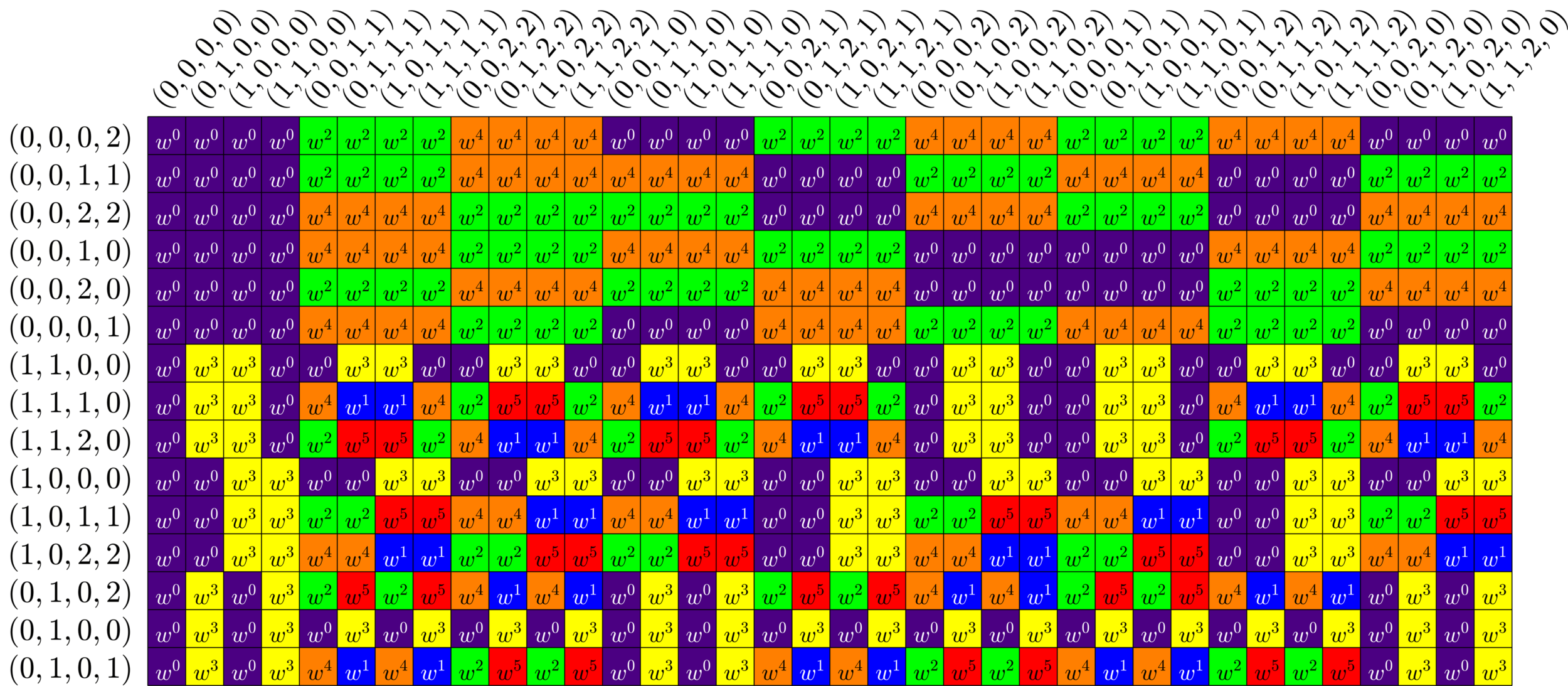
Tremain ETFs




\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]
\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]

\(\bigotimes\)

\(\sqrt{2}\)
\(\sqrt{\dfrac{1}{2}}\)
\(\sqrt{\dfrac{3}{2}}\)


Hadamard matrix
Hadamard matrix
Steiner Triple System
Tremain ETFs






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)
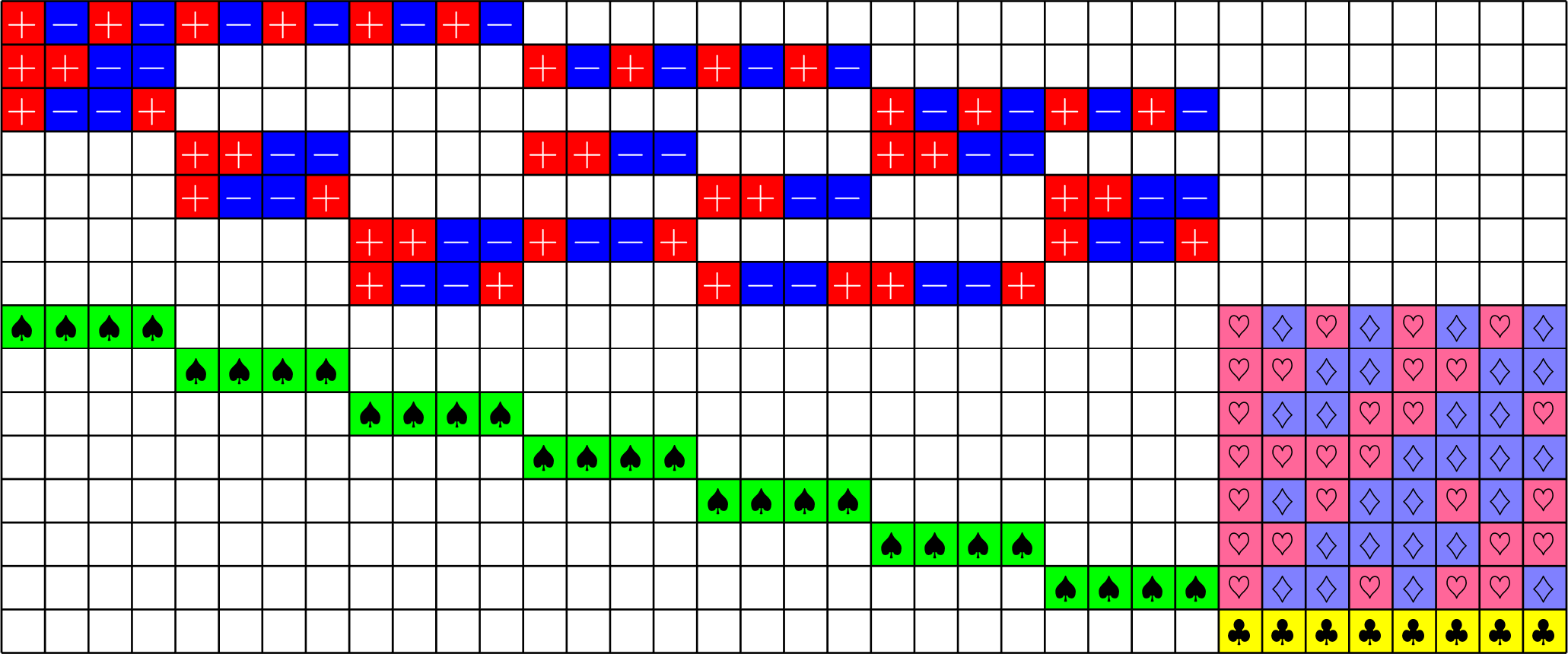
Tremain ETFs:
Theorem (Fickus, J,Mixon, Peterson '18). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),
then there exists a \((2,3,2h-1)\)-Steiner system
and by the Tremain construction there exists a real \(d\times N\) ETF where \[d=\frac{1}{3}(h+1)(2h+1),\qquad N=h(2h+1).\]



\(51\times 136\) Tremain ETF
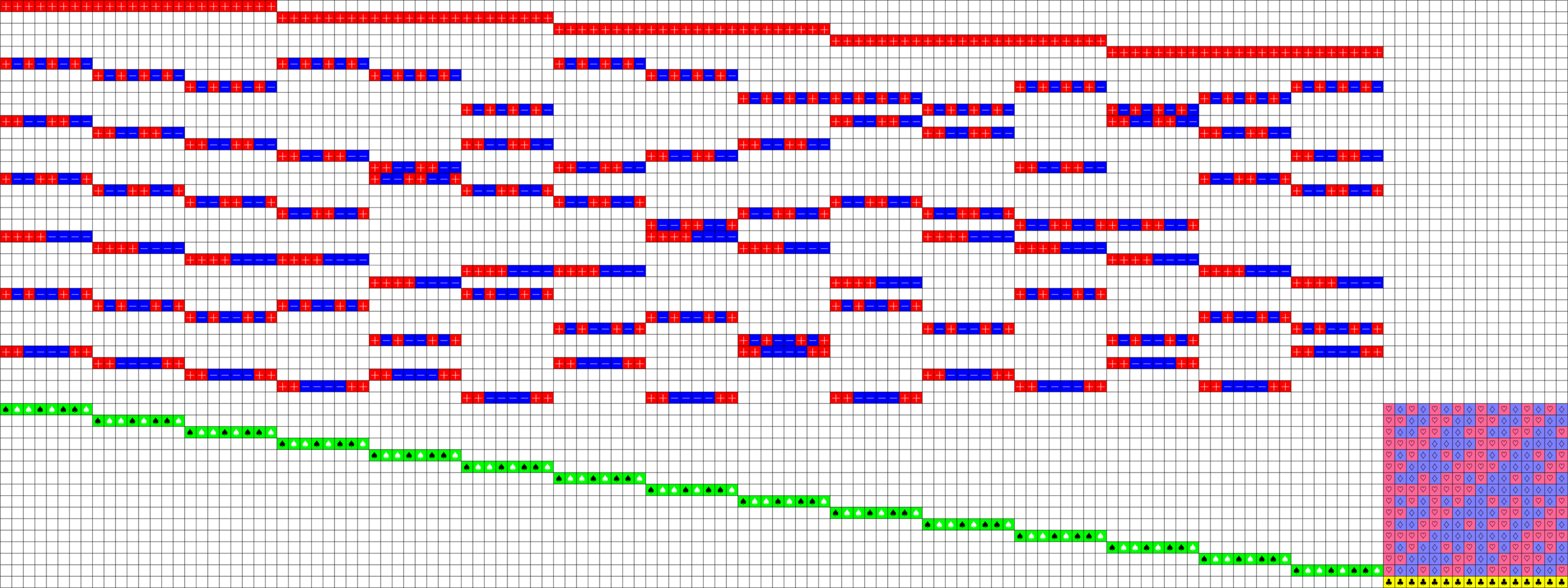
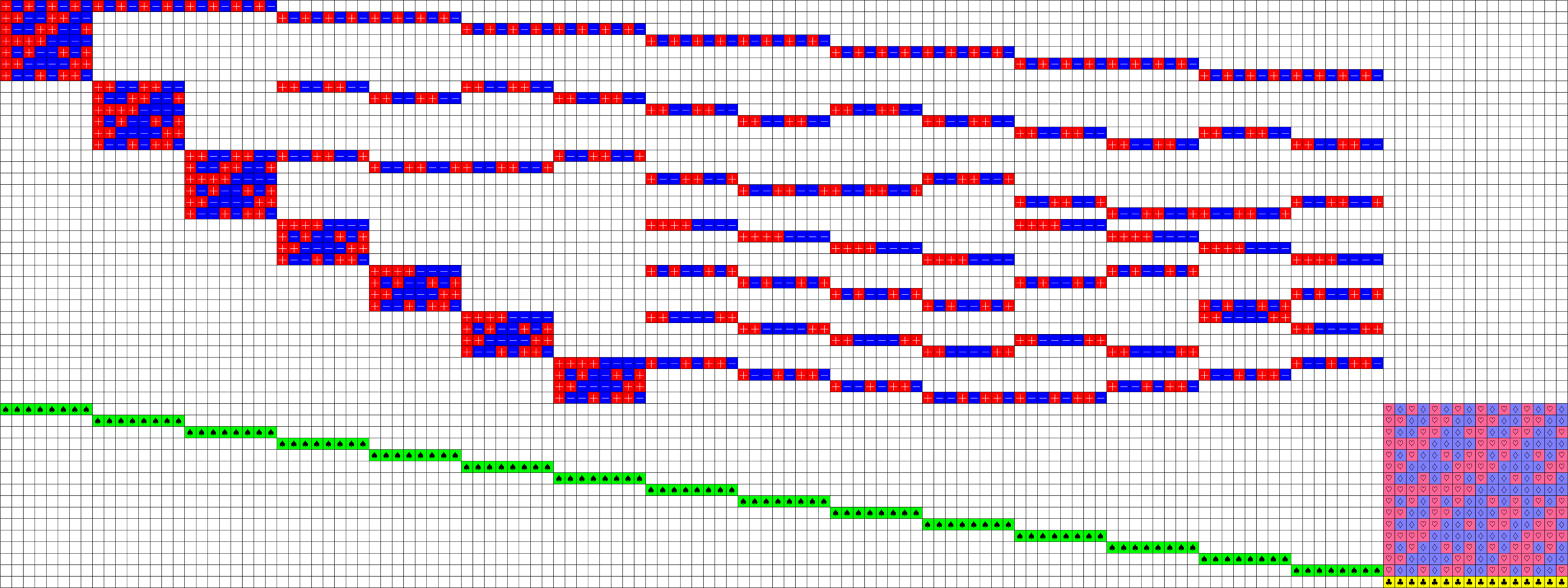






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
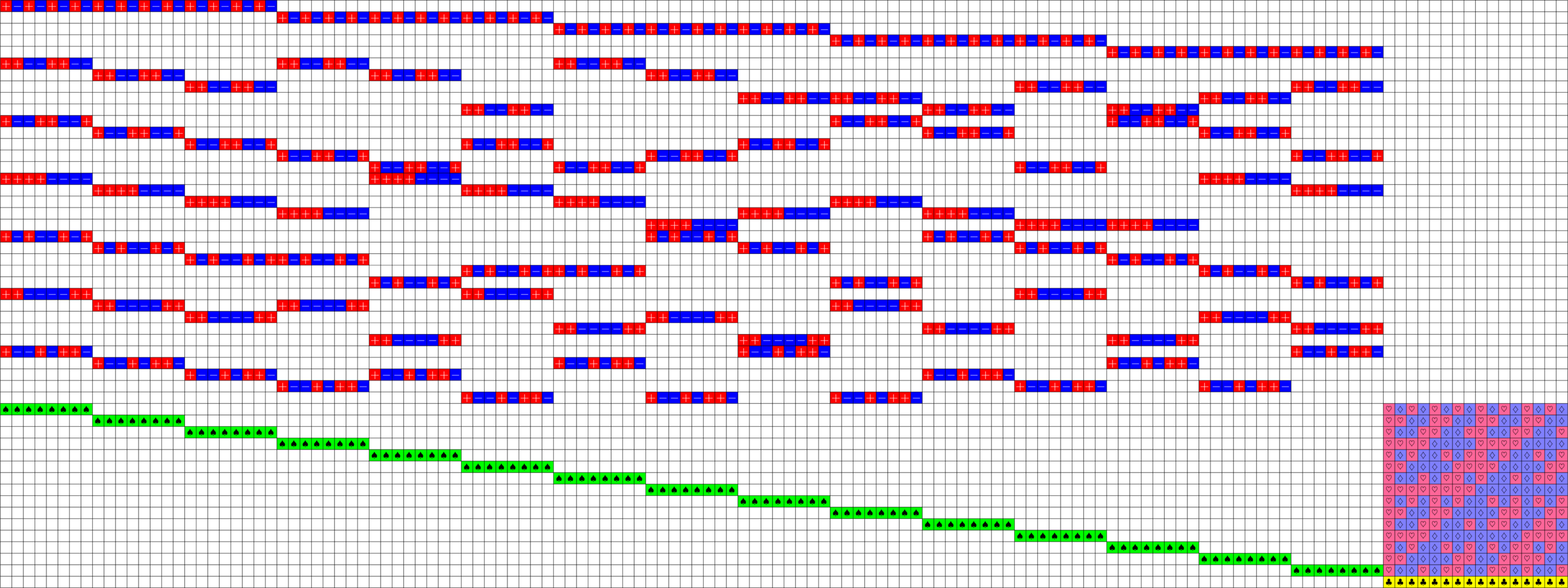
Axial Tremain ETFs:
Theorem (Fickus, J,Mixon, Peterson '18). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 2\) \(\text{mod}\ 3\),
then there exists a strongly regular graph with parameters:
\[v=h(2h+1),\ k=\frac{(h+2)(2h-1)}{2},\ \lambda=\frac{(h-1)(h+4)}{2},\ \mu = \frac{h(h+2)}{2}\]


This gave us a new ETF!
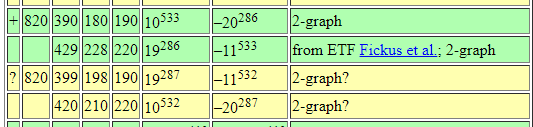
From Brouwer's table online:
How can I make these vectors sum to zero?






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


The Bible



These are the graphs associated with a real \(15\times 36\) ETF.
\(NO_{6}^{-}(2)\)
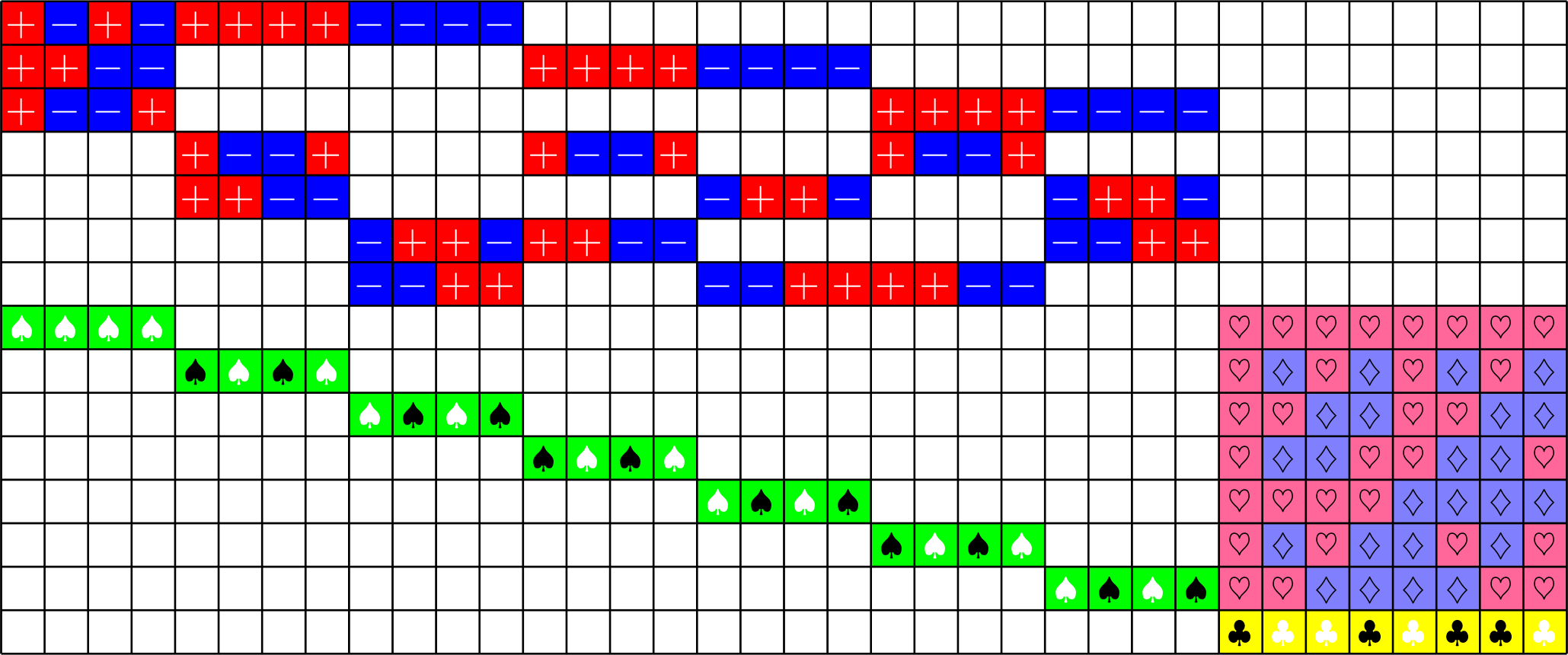






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
\(NO_{6}^{-}(2)\)

- \(\mathbf{1} = [1\ 1\ \cdots\ 1]^{\top}\) is in the kernel.
- This gives us a strongly regular graph on 36 vertices.
- This can be generalized to all other Tremain ETFs.
Centered Tremain ETFs:
Theorem (J). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 1\) or \(2\) \(\text{mod}\ 3\),
then there exists a strongly regular graph with parameters:
\[v=h(2h+1),\quad k=h^2-1,\quad \lambda=\frac{1}{2}(h^2-4),\quad \mu = \frac{1}{2}h(h-1)\]


There exists a \(20\times 20\) Hadamard matrix, and hence an SRG(820,399,198,190), which is new!

From Brouwer's table online:

\(\bigotimes\)

\[\left[\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right.\]
\[\left.\begin{array}{l} \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right]\]
\(I_{3}\otimes\)(\(2\times 3\) ETF)
Hadamard Matrix
Group Divisible Design (GDD)
Group Divisible Design






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
Group Divisible Design






\(\ =+1\)
\(\ =-1\)
\(\ =\sqrt{2}\)
\(\ =-\sqrt{\dfrac{1}{2}}\)
\(\ =+\sqrt{\dfrac{1}{2}}\)
\(\ =\sqrt{\dfrac{3}{2}}\)


\(\ =-\sqrt{2}\)
\(\ =-\sqrt{\dfrac{3}{2}}\)
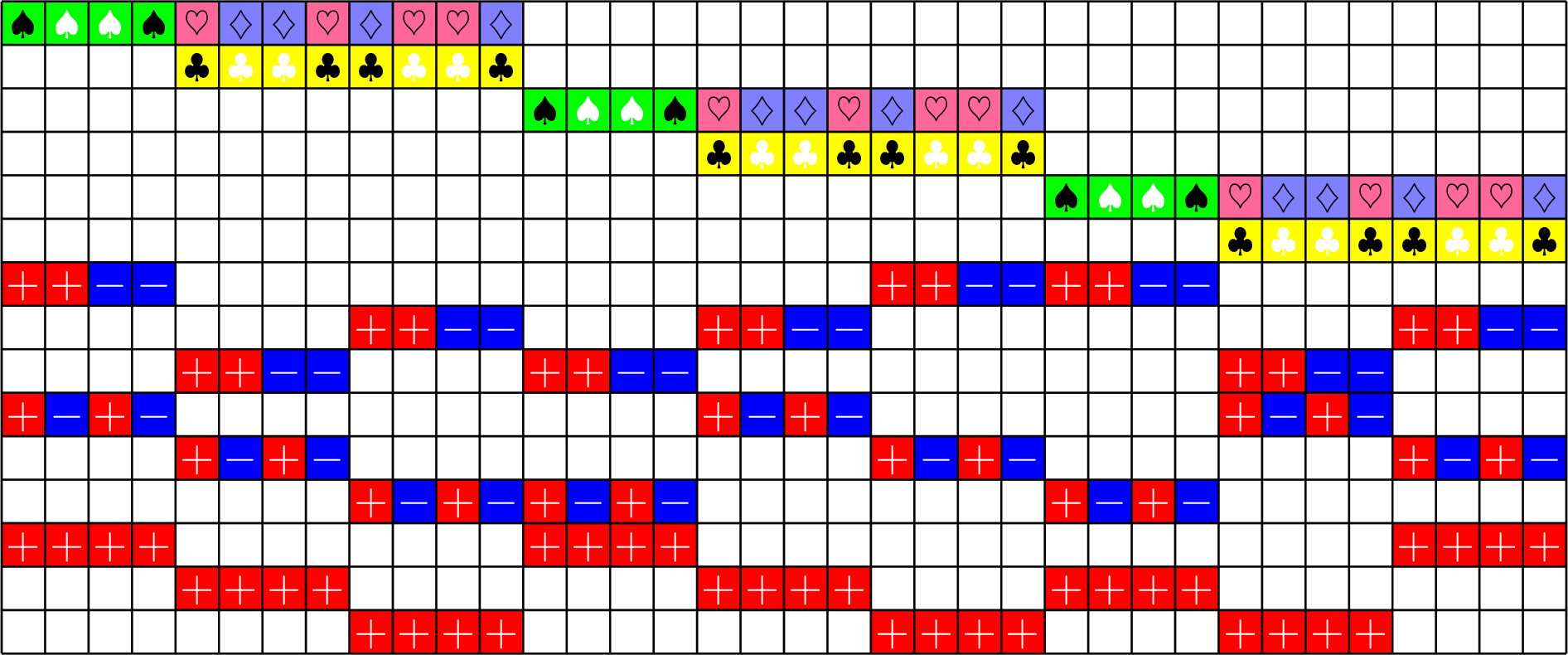
Axial GDD ETFs:
Theorem (J). If there exists an
\(h\times h\) Hadamard matrix with \(h\equiv 1\) \(\text{mod}\ 3\),
then there exists a strongly regular graph with parameters:
\[v=h(2h+1),\ k=\frac{(h+2)(2h-1)}{2},\ \lambda=\frac{(h-1)(h+4)}{2},\ \mu = \frac{h(h+2)}{2}\]


There exists a \(16\times 16\) Hadamard matrix, and hence an SRG(528,279,150,144), which is new!
From Brouwer's table online:

\(3\)-Negative ETFs
2
5
15
51
77
145
187
287
345
477
551
715
3
10
36
136
210
406
528
820
990
1378
1596
2080
\(d\)
\(N\)
Exists
Centered
Axial
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
?
?
?
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
?
?
?
?
?
?
Finding an axial \(77\times 210\)
- Let \(\Phi\) be the known centered \(77\times210\).
- We want to find \(x = \operatorname{argmin}_{\|x\|_{2} = 1}\|\Phi^{\top}x\|_{\infty}\)
- Instead we find \(x = \operatorname{argmin}_{\|x\|_{2} = 1}\|\Phi^{\top}x\|_{4}\)
- Run gradient descent on many random starting vectors
- If \(\Phi^{\top}x\) is a \(\pm1\) vector \(\Rightarrow\) Profit!
Theorem (J). There exists an SRG(210,95,40,45)
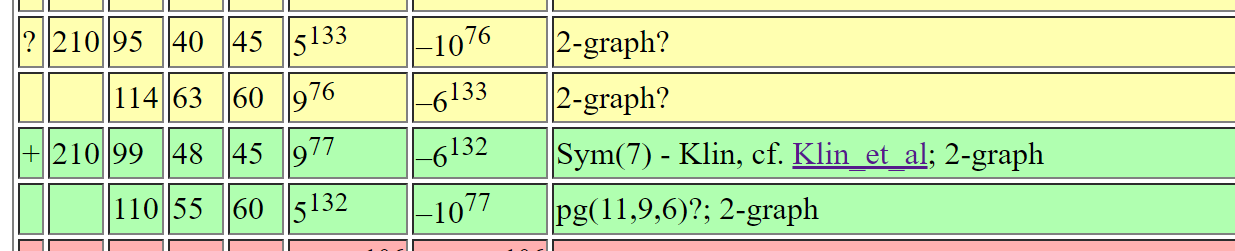
From Brouwer's table online:
Thanks!
- This work was partially supported by NSF #1830066
- Webpage: https://sites.google.com/view/john-jasper-math/home
- Slides: https://slides.com/johnjasper



What species is this?
*ETF table by Dustin Mixon and Matt Fickus
, Spence difference set
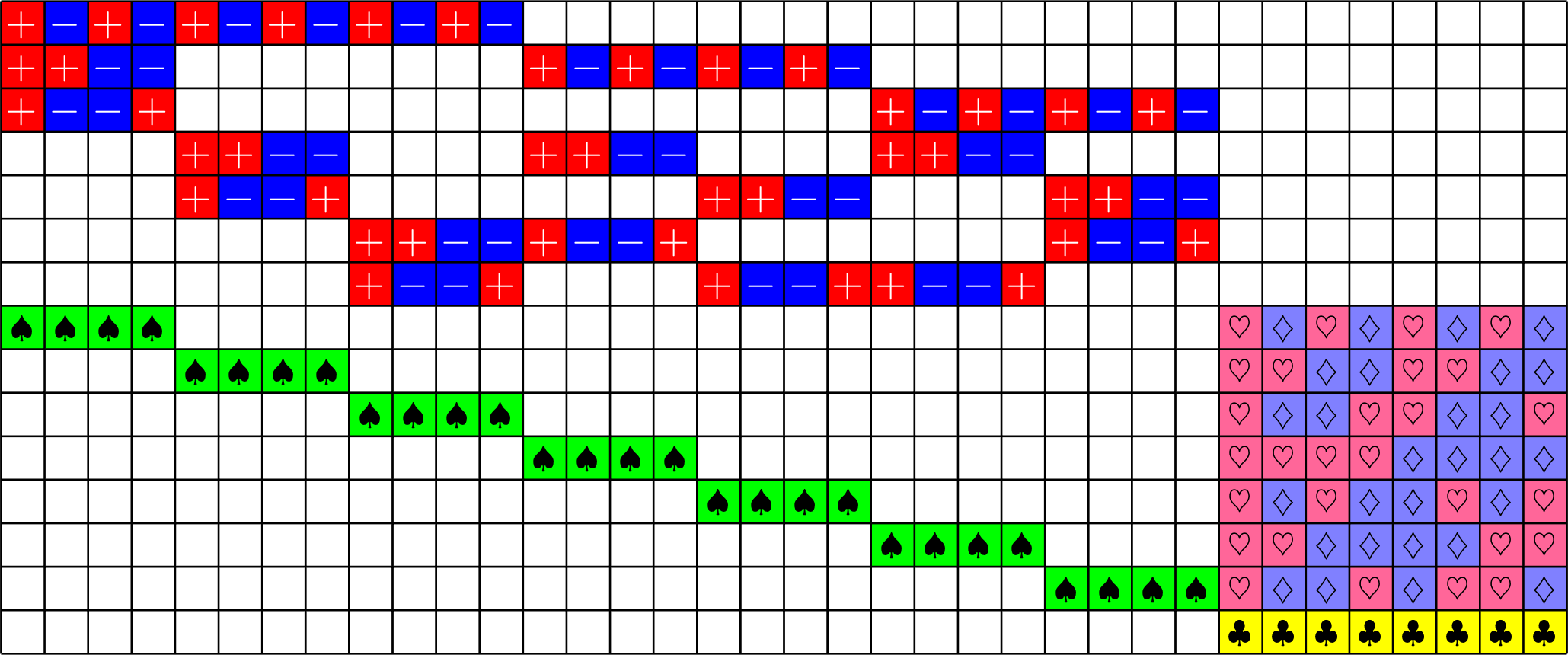
\[\begin{array}{c|cccccc} & (0,0,0,1) & (1,1,0,1) & (0,0,1,0) & (1,0,1,0) & (0,0,1,1) & (0,1,1,1)\\ \hline (0,0,0,1) & (0,0,0,0) & (1,1,0,0) & (0,0,1,1) & (1,0,1,1) & (0,0,1,0) & (0,1,1,0)\\ (1,1,0,1) & (1,1,0,0) & (0,0,0,0) & (1,1,1,1) & (0,1,1,1) & (1,1,1,0) & (1,0,1,0)\\ (0,0,1,0) & (0,0,1,1) & (1,1,1,1) & (0,0,0,0) & (1,0,0,0) & (0,0,0,1) & (0,1,0,1)\\ (1,0,1,0) & (1,0,1,1) & (0,1,1,1) & (1,0,0,0) & (0,0,0,0) & (1,0,0,1) &(1,1,0,1)\\ (0,0,1,1) & (0,0,1,0) & (1,1,1,0) & (0,0,0,1) & (1,0,0,1) & (0,0,0,0) & (0,1,0,0)\\ (0,1,1,1) & (0,1,1,0) & (1,0,1,0) & (0,1,0,1) & (1,1,0,1) & (0,1,0,0) & (0,0,0,0) \end{array}\]
\[D=\{(0,0,0,1),(0,0,1,0),(0,0,1,1),(0,1,1,1),(1,0,1,0),(1,1,0,1)\}\]
is a (McFarland) difference set in \(G=\Z_{2}\times\Z_{2}\times\Z_{2}\times\Z_{2}\)
A McFarland difference set
Each nonzero element appears exactly twice in the difference table:
A McFarland difference set
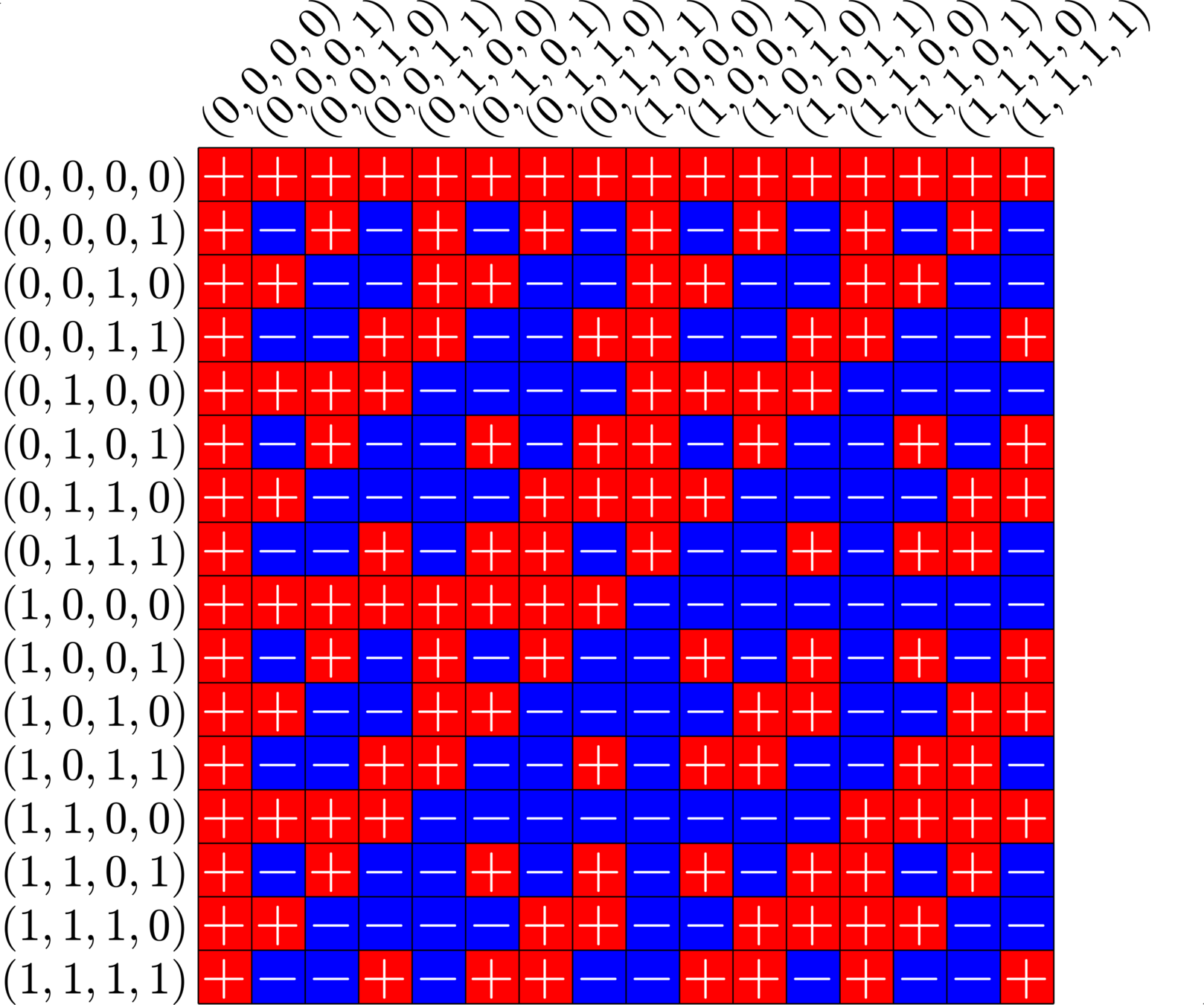
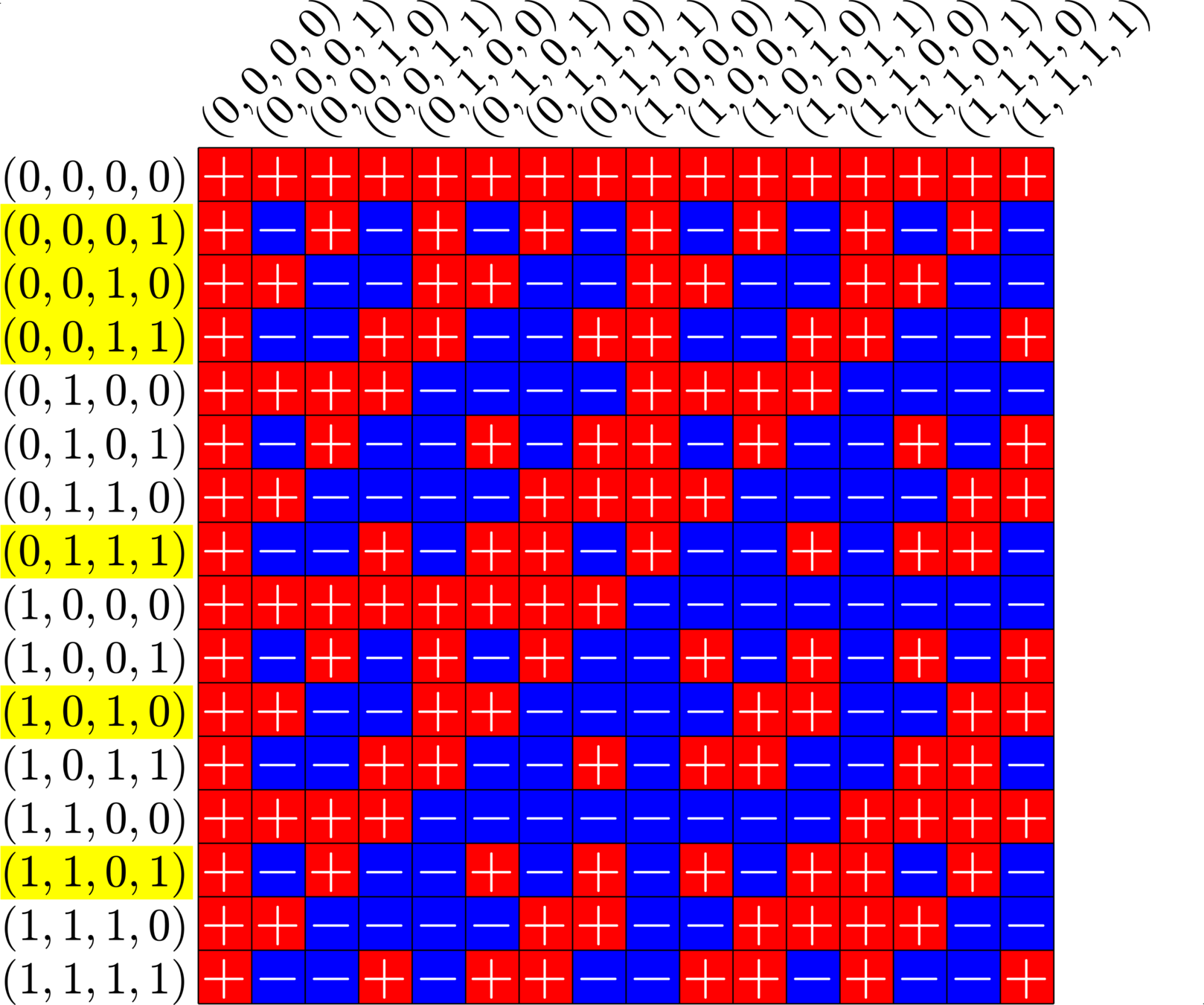
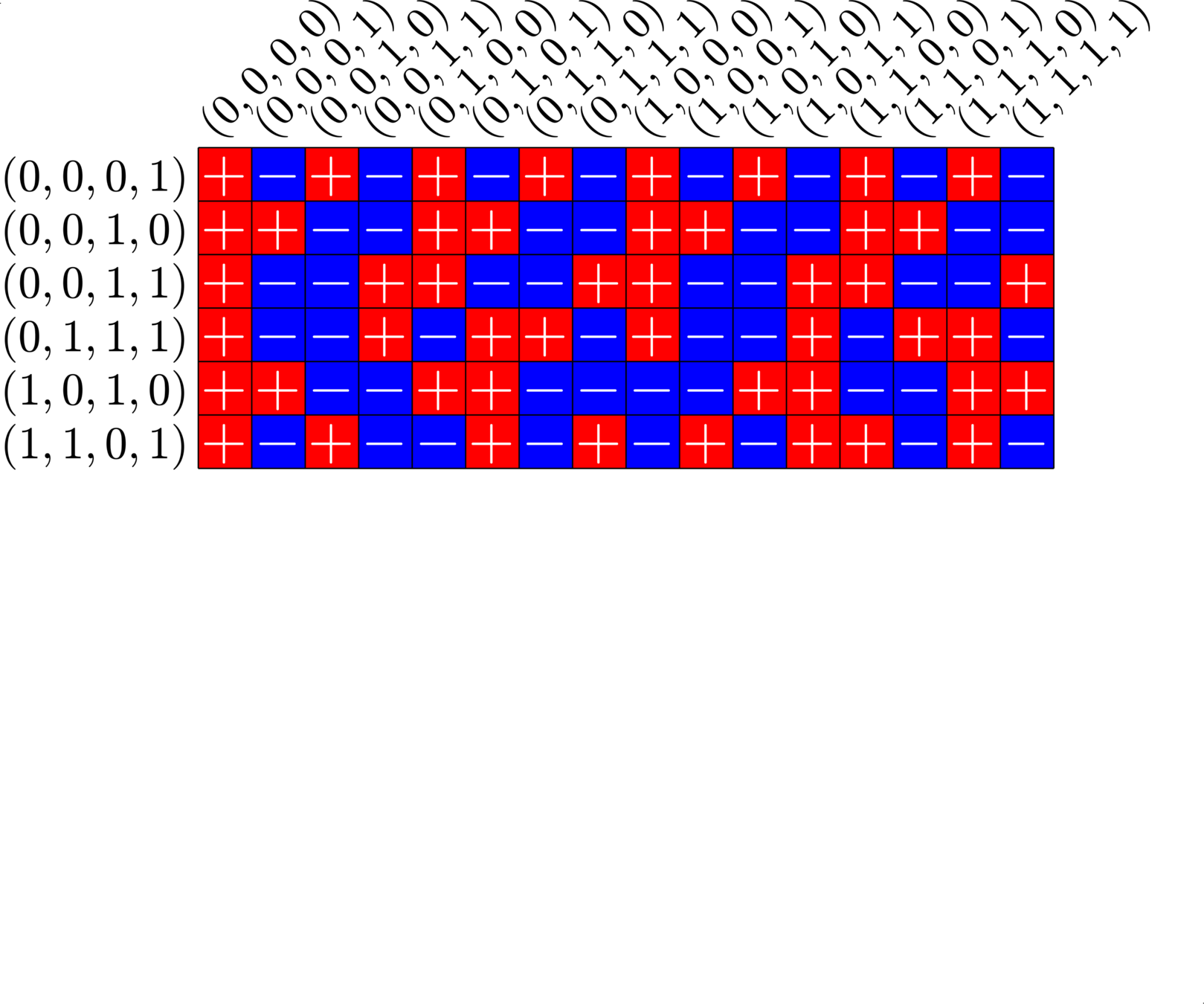
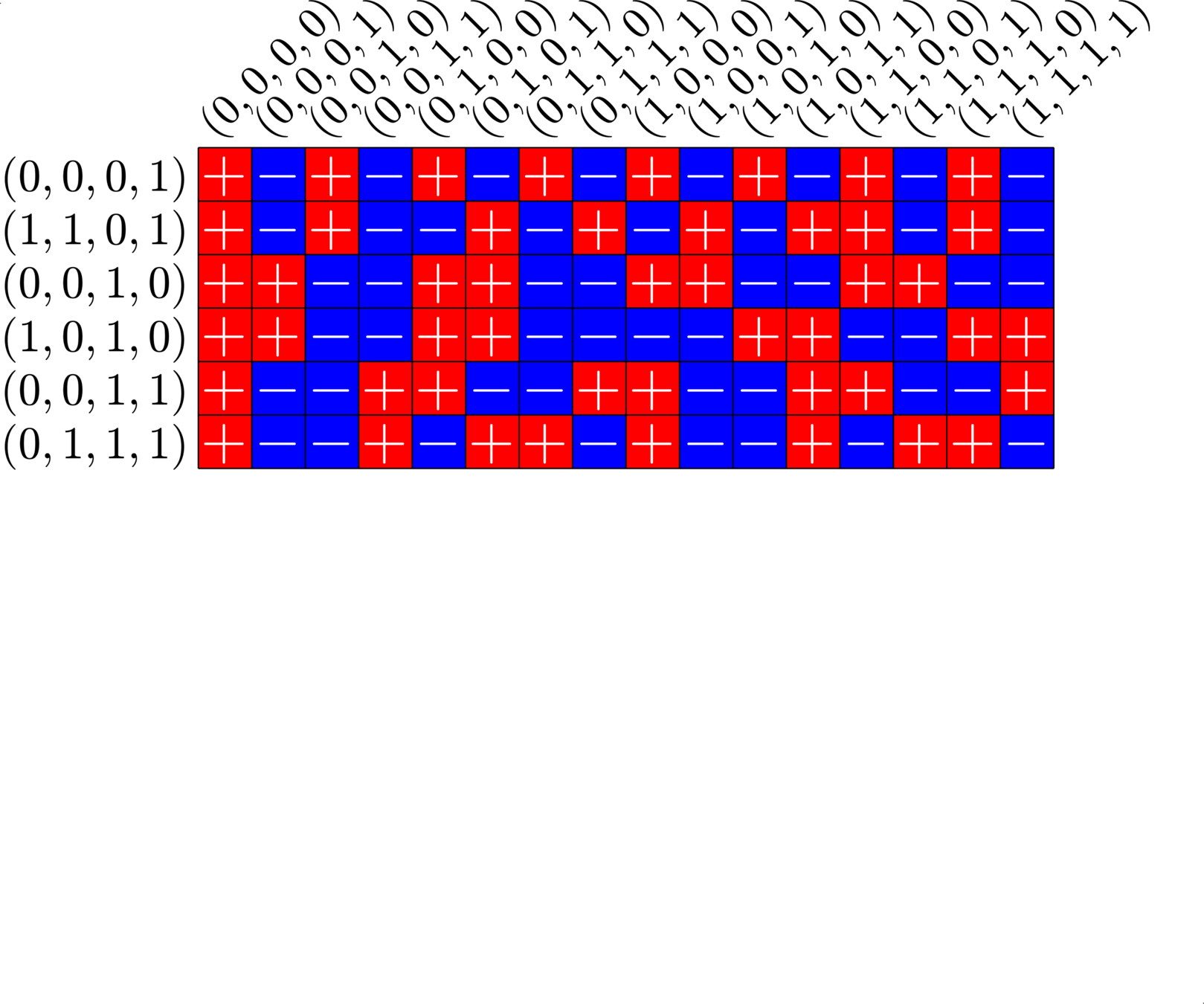
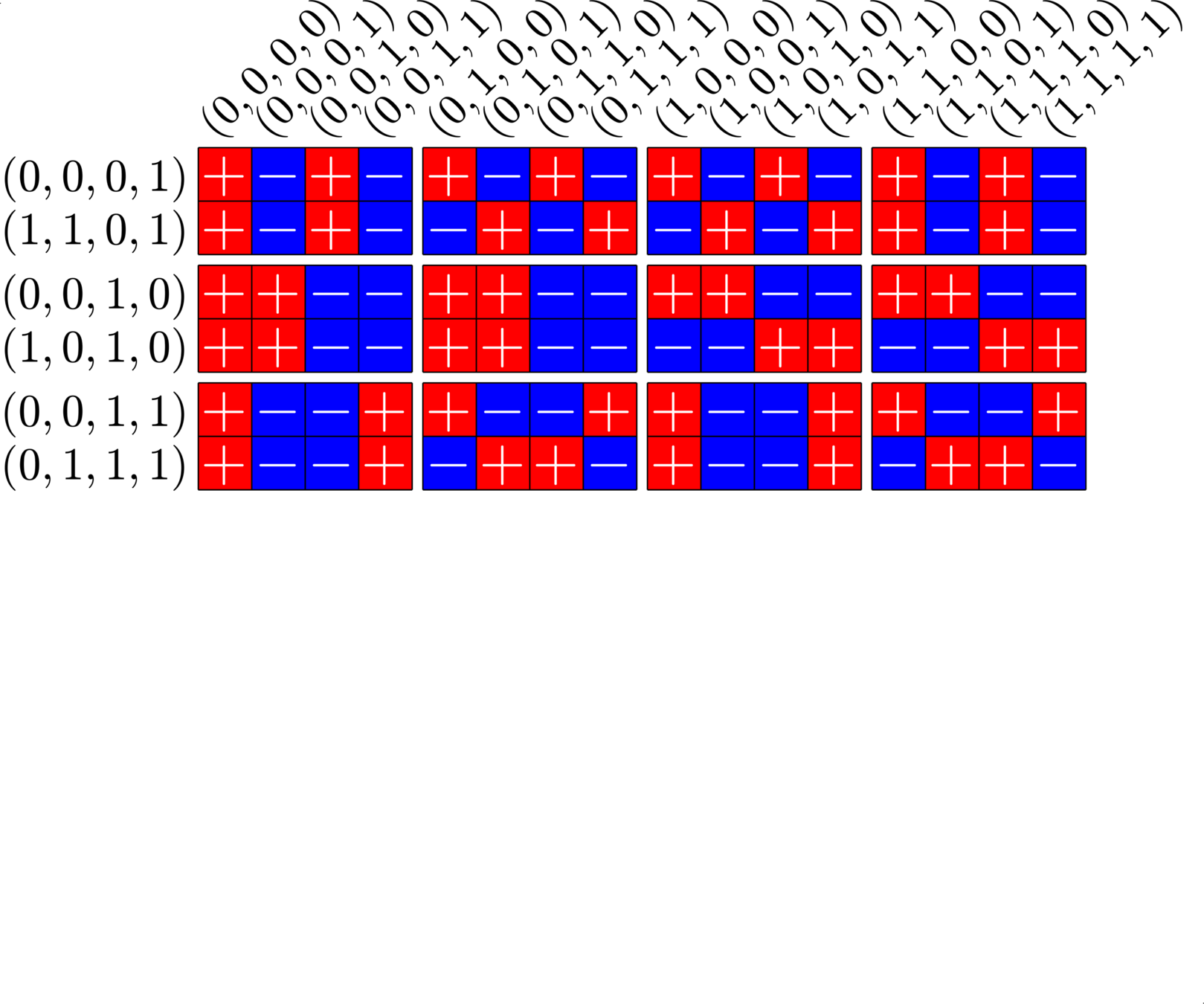


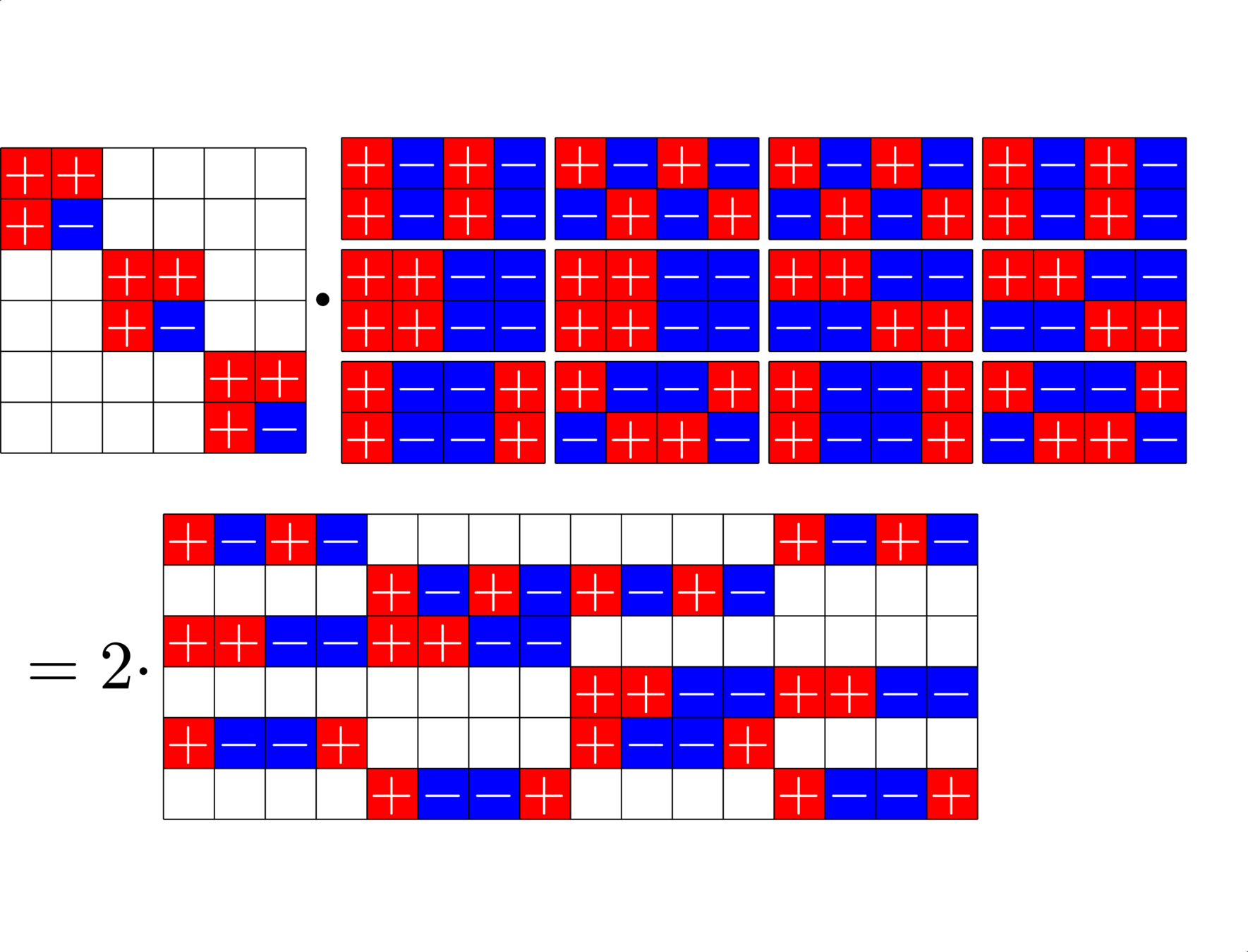
This \(6\times 16\) ETF from a McFarland difference set is also a Steiner ETF


What species is this?
*ETF table by Dustin Mixon and Matt Fickus
, Spence difference set


GDD ETF:
Tremain ETF:
A New Species!
ETFs from GDDs
Theorem (Fickus, JJ '19). Given a
\(d\times n\) ETF


\(k\)-GDD of type \(M^{U}\)
and
provided certain integrality conditions hold, there exists a \(D\times N\) ETF with \(D>d\), \(N>n\) and \(\frac{D}{N}\approx \frac{d}{n}.\)

A New ETF
This GDD
Combined with a \(6\times 16\) ETF, like this one:

produces a complex \(266\times 1008\) ETF, which appears to be new!
\(v=6m+3\)
\(k=3\)
\(r = \frac{v-1}{k-1} = \frac{6m+2}{2} = 3m+1\)
\(b = \frac{vr}{k} = \frac{(6m+3)(3m+1)}{3} = (2m+1)(3m+1)\)
\(\frac{b}{r} = (2m+1)\)
\(H=3m+1\)
\(d = 2\frac{b}{r} + b-\frac{b}{r} = (2m+1)(3m+1) + (2m+1) = (2m+1)(3m+2)\)
\(N = vH = (6m+3)(3m+1) = 3(2m+1)(3m+1)\)
\(N-1 = 3(2m+1)(3m+1) - 1 = 18m^2+15m+2 = (3m+2)(6m+1)\)
\(\alpha=\frac{N}{d} = \frac{ 3(2m+1)(3m+1)}{(2m+1)(3m+2)} = \frac{ 3(3m+1)}{(3m+2)}\)
\(\beta^2 = \frac{N-d}{d(N-1)} = \frac{3(2m+1)(3m+1) - (2m+1)(3m+2)}{ (2m+1)(3m+2)\big(3(2m+1)(3m+1)-1\big)} = \frac{3(3m+1) - (3m+2)}{ (3m+2)\big(3(2m+1)(3m+1)-1\big)}\)
\( = \frac{6m+1}{(3m+2)\big(18m^2+15m+2\big)} = \frac{6m+1}{(3m+2)(3m+2)(6m+1)} = \frac{1}{(3m+2)^2}\)
\(K = \frac{N-1}{2}+\frac{\alpha-1}{2\beta} = \frac{1}{2}\left((3m+2)(6m+1)+\left(\frac{ 3(3m+1)}{3m+2}-1\right)(3m+2)\right)\)
\( = \frac{1}{2}\left((3m+2)(6m+1)+\left(6m+1)\right)\right) = \frac{1}{2}(3m+3)(6m+1)\)
Vectors that are as spread out as possible
Theorem (the Welch bound). Given a collection of unit vectors
\(\Phi=(\varphi_{i})_{i=1}^{N}\) in \(\mathbb{C}^d\), the coherence satisfies
\[\mu(\Phi):=\max_{i\neq j}|\langle \varphi_{i},\varphi_{j}\rangle|\geq \sqrt{\frac{N-d}{d(N-1)}}.\]
Equality holds if and only if the following two conditions hold:
- Tight: There is a constant \(A>0\) such that \[\sum_{i=1}^{N}|\langle v,\varphi_{i}\rangle|^{2} = A\|v\|^{2} \quad\text{for all } v.\]
- Equiangular: There is a constant \(\alpha\) such that \[|\langle\varphi_{i},\varphi_{j}\rangle| = \alpha\quad\text{for all }i\neq j.\]
A collection of equal norm vectors which is both equiangular and tight is known as an equiangular tight frame (ETF). These are also known as Welch bound equality codes.
\(f(x) = \|\Phi x\|_{p}^{p}\)
\(\frac{\|\Phi (x+h)
AMS Cincinnati Spring 2023
By John Jasper
AMS Cincinnati Spring 2023
- 517



