Day 17:

Orthogonal projections and Gram-Schmidt

Norms

Definition. Given an inner product space \(V\) and a vector \(v\in V\), then norm of \(v\) is the number

\[\|v\| = \sqrt{\langle v,v\rangle}.\]

Orthonormal bases

Definition. Let \(V\) be an inner product space. A set \(\mathcal{B}=\{v_{1},\ldots,v_{k}\}\subset V\) is called an orthonormal basis for \(V\) if \(\mathcal{B}\) is a basis for \(V\) and for \(i,j\in\{1,2,\ldots,k\}\)

\[\langle v_{i},v_{j}\rangle = \begin{cases} 1 & i=j,\\ 0 & i\neq j.\end{cases}\]

Orthonormal bases

Example. In \(\mathbb{P}_{2}\) with inner product

\[\langle f(x),g(x)\rangle = \int_{0}^{1} f(x)g(x)\,dx\]

the set \(\{1,x,x^2\}\) is a basis, but it is not an orthonormal basis. Indeed, note that

\[\langle 1,x\rangle = \int_{0}^{1}x\,dx = \frac{1}{2}.\]

Example. In \(\mathbb{P}_{2}\) with inner product

\[\langle f(x),g(x)\rangle = \int_{-1}^{1} f(x)g(x)\,dx\]

the set \[\left\{\frac{\sqrt{2}}{2},\frac{\sqrt{6}}{2}x,\frac{\sqrt{10}}{4}(3x^2-1)\right\}\] is an orthonormal basis. (Check it yourself)

Orthogonal bases

In some cases it is more convenient not to use a basis where the norms of the vectors are not all \(1\).

 

Definition. Given a vector \(v\) in an inner product space \(V\), the vector \(v\) is called normalized if \(\|v\|=1\). Given \(v\neq 0\), the vector \(\frac{v}{\|v\|}\) is called the normalized vector in the direction of \(v\).

Definition. If \(V\) is an inner product space, and \(\mathcal{B}:=\{v_{1},v_{2},\ldots,v_{k}\}\subset V\), then we call \(\mathcal{B}\) an orthogonal basis for \(V\) if \(\mathcal{B}\) is a basis for \(V\) and \[\left\{\frac{v_{1}}{\|v_{1}\|}\frac{v_{2}}{\|v_{2}\|},\ldots,\frac{v_{k}}{\|v_{k}\|}\right\}\] is an orthonormal basis for \(V\).

Example. In \(\mathbb{P}_{2}\) with inner product with the inner product from the last example, the set \(\left\{1,x,3x^2-1\right\}\) is an orthogonal basis for \(\mathbb{P}_{2}\).

Orthonormal bases

Let \(V\) be a subspace of \(\R^{n}\). Assume \(\mathcal{B}=\{v_{1},\ldots,v_{k}\}\) is an orthonormal basis for \(V\). Define the matrix

\[A = \begin{bmatrix} v_{1} & v_{2} & \cdots & v_{k}\end{bmatrix}.\]

 

Let \(v\in V.\) Since \(\mathcal{B}\) is a basis, there are unique scalars \(\alpha_{1},\ldots,\alpha_{k}\) such that

\[v = \alpha_{1}v_{1} + \alpha_{2}v_{2} + \cdots +\alpha_{k}v_{k}.\]

However, if we take a dot product:

\(v_{i}\cdot v = v_{i}\cdot\big(\alpha_{1}v_{1} + \alpha_{2}v_{2} + \cdots +\alpha_{k}v_{k}\big)\)

                                   \(= \alpha_{1}(v_{i}\cdot v_{1}) + \alpha_{2}(v_{i}\cdot v_{2}) + \cdots +\alpha_{k}(v_{i}\cdot v_{k}) = \alpha_{i}\)

 

Hence, the coefficient on \(v_{i}\) must be the scalar \(v_{i}\cdot v\). That is,

\[v = \sum_{i=1}^{k}(v_{i}\cdot v) v_{i} = \sum_{i=1}^{k}(v_{i}^{\top}v) v_{i}= AA^{\top}v.\]

Orthonormal bases

Additionally, for any \(v\in V\) we have

\[ = \left(\sum_{i=1}^{k} (v_{i}\cdot v) v_{i}^{\top}\right)\left(\sum_{j=1}^{k} (v_{j}\cdot v) v_{j}\right)\]

\[ =\sum_{i=1}^{k}\sum_{j=1}^{k} (v_{i}\cdot v) v_{i}^{\top}(v_{j}\cdot v) v_{j}\]

\[ =\sum_{i=1}^{k}|v_{i}\cdot v|^2\]

\[ =\sum_{i=1}^{k}\sum_{j=1}^{k} (v_{i}\cdot v)(v_{j}\cdot v) v_{i}^{\top} v_{j}\]

\[\|v\|^{2}  = v^{\top}v= \left(\sum_{i=1}^{k} (v_{i}\cdot v) v_{i}\right)^{\top}\left(\sum_{j=1}^{k} (v_{j}\cdot v) v_{j}\right)\]

Another way to state this is \(\|v\| = \|A^{\top}v\|\).

Orthonormal bases

Additionally, for any \(v\in V\) we have

\[ = \left(\sum_{i=1}^{k} (v_{i}\cdot v) v_{i}^{\top}\right)\left(\sum_{j=1}^{k} (v_{j}\cdot v) v_{j}\right)\]

\[ =\sum_{i=1}^{k}\sum_{j=1}^{k} (v_{i}\cdot v) v_{i}^{\top}(v_{j}\cdot v) v_{j}\]

\[ =\sum_{i=1}^{k}|v_{i}\cdot v|^2\]

\[ =\sum_{i=1}^{k}\sum_{j=1}^{k} (v_{i}\cdot v)(v_{j}\cdot v) v_{i}^{\top} v_{j}\]

\[\|v\|^{2}  = v^{\top}v= \left(\sum_{i=1}^{k} (v_{i}\cdot v) v_{i}\right)^{\top}\left(\sum_{j=1}^{k} (v_{j}\cdot v) v_{j}\right)\]

Another way to state this is \(\|v\| = \|A^{\top}v\|\).

Theorems about norms and inner products

 

Theorem (The polarization identity). If \(V\) is an inner product space, and \(v,w\in V\), then

\[\|v+w\|^{2} = \|v\|^{2}+2\langle v,w\rangle + \|w\|^{2}\]

and thus

\[\langle v,w\rangle = \frac{1}{2}\left(\|v+w\|^2 - \|v\|^{2} - \|w\|^{2}\right).\]

Proof. Using the properties of an inner product we have

\[\|v+w\|^{2} = \langle v+w,v+w\rangle = \langle v,v+w\rangle + \langle w,v+w\rangle\]

\[=\langle v,v\rangle + \langle v,w\rangle + \langle w,v\rangle + \langle w,w\rangle\]

\[=\|v\|^2 + \langle v,w\rangle + \langle v,w\rangle + \|w\|^2\]

\[=\|v\|^2 + 2\langle v,w\rangle + \|w\|^2.\]

The other conclusion follows by rearranging the first equality. \(\Box\)

Theorem (the Pythagorean Theorem). Suppose \(V\) is an inner product space and \(v,w\in V\). Then, \(\langle v,w\rangle= 0\) if and only if

\[\|v\|^{2} + \|w\|^2 = \|v+w\|^2.\]

Proof. By the polarization identity \[\|v+w\|^{2} = \|v\|^{2}+2\langle v,w\rangle + \|w\|^{2}\]

\(\Box\)

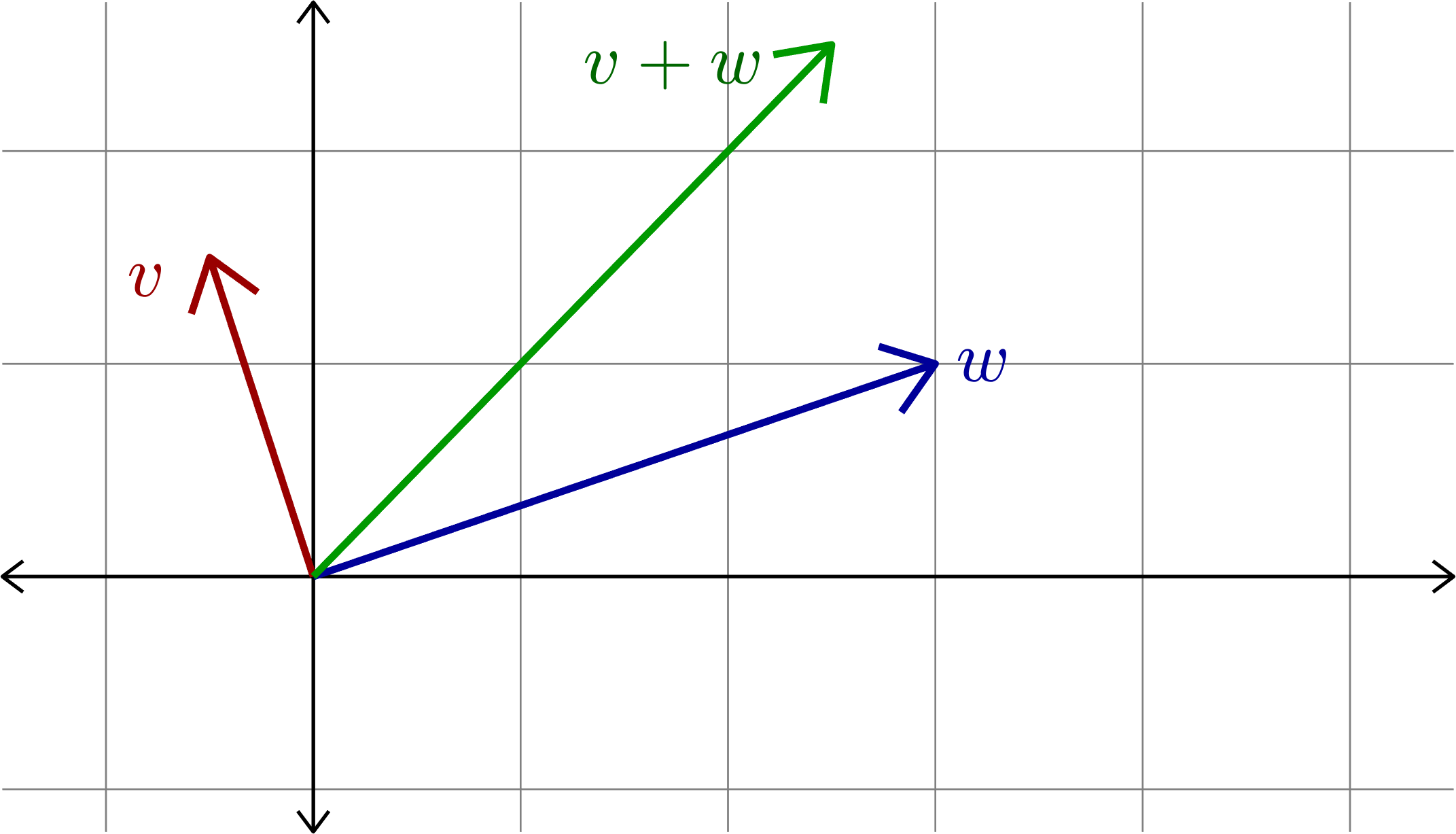
Theorem (the Cauchy-Schwarz inequality). Suppose \(V\) is an inner product space. If \(v,w\in V\), then

\[|\langle v,w\rangle|\leq \|v\|\|w\|.\]

Moreover, if equality occurs, then \(v\) and \(w\) are dependent.

Proof. If \(v=0\) then both sides of the inequality are zero, hence we are done. Moreover, note that \(v\) and \(w\) are dependent.

Suppose \(v\neq 0\). Define the scalar \(c = \frac{\langle v,w\rangle}{\|v\|^2}\), and compute

\[ \]

\[ = \|w\|^{2} - 2\frac{\langle v,w\rangle}{\|v\|^2}\langle w,v\rangle + \frac{|\langle v,w\rangle|^2}{\|v\|^4}\|v\|^{2}  = \|w\|^{2} - \frac{|\langle v,w\rangle|^2}{\|v\|^2}\]

\[0 \leq \|w-cv\|^{2} = \|w\|^{2} - 2\langle w,cv\rangle + \|cv\|^{2} = \|w\|^{2} - 2c\langle w,v\rangle + c^2\|v\|^{2}\]

Rearranging this inequality we have

\[\frac{|\langle v,w\rangle|^2}{\|v\|^2}\leq \|w\|^{2}.\]

Note, if this inequality is actually equality, then we have \(\|w-cv\|=0\), that is \(w-cv=0\). This implies \(v\) and \(w\) are dependent. \(\Box\)

Theorem (the Triangle inequality). Suppose \(V\) is an inner product space. If \(v,w\in V\), then

\[\|v+w\|\leq \|v\|+\|w\|.\]

Moreover, if equality occurs, then \(v\) and \(w\) are dependent.

Proof. First, note that \(\langle v,w\rangle\leq |\langle v,w\rangle|\). Using the polarization identity and the Cauchy-Schwarz inequality we have

 

 

\[\leq \|v\|^{2} + 2\|v\|\|w\| + \|w\|^{2} = \big(\|v\|+\|w\|\big)^{2}.\]

\[\leq \|v\|^{2} + 2|\langle v,w\rangle| + \|w\|^{2}.\]

\[\|v+w\|^{2} = \|v\|^{2}+2\langle v,w\rangle + \|w\|^{2}\]

Note that if \(\|v+w\|=\|v\|+\|w\|\), then we must have

\[\|v\|^{2} + 2|\langle v,w\rangle| + \|w\|^{2} = \|v\|^{2} + 2\|v\|\|w\| + \|w\|^{2}\]

and thus \(|\langle v,w\rangle|=\|v\|\|w\|\). By the Cauchy-Schwarz inequality, this implies \(v\) and \(w\) are dependent. \(\Box\)

Quiz. 

1. For \(x,y\in\mathbb{R}^{2}\) such that \(\langle x,y\rangle = 2\) it _______________ holds that \(\|x\|=\|y\|=1\).
2. For \(x,y\in\mathbb{R}^{2}\) such that \(\langle x,y\rangle = 0\) it _______________ holds that \(|\langle x,y\rangle| = \|x\|\|y\|\).
3. For normalized \(x,y\in\mathbb{R}^{2}\) such that \(\|x+y\|^{2} = \|x\|^{2} + \|y\|^{2}\) it _______________ holds that \(|\langle x,y\rangle| = \|x\|\|y\|\).
4. For nonzero vectors \(x,y\in\mathbb{R}^{n}\) it _______________ holds that \(\|x+y\|^{2} = \|x\|^{2}+\|y\|^{2}\) and \(\|x+y\|=\|x\|+\|y\|\).