Day 19:
The projection theorem
What if \(Ax=b\) has no solution?
Example: Consider the equation
\[\begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\end{bmatrix} = \begin{bmatrix} 3\\ 5\\ 7\\ 9\end{bmatrix}\]
This equation has a unique solution \(\mathbf{x}=[1\ \ 2]^{\top}\).
This equation has a solution since
\[\begin{bmatrix} 3\\ 5\\ 7\\ 9\end{bmatrix}\in C\left(\begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\end{bmatrix}\right) = \text{span}\left\{\begin{bmatrix} 1\\ 1\\ 1\\ 1\end{bmatrix},\begin{bmatrix} 1\\ 2\\ 3\\ 4\end{bmatrix}\right\}\]
What if \(Ax=b\) has no solution?
Example: Consider the equation
\[\begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\end{bmatrix} = \begin{bmatrix} 3.1\\ 4.8\\ 7.13\\ 9\end{bmatrix}\]
This equation has NO a solution since
\[\begin{bmatrix} 3.1\\ 4.8\\ 7.13\\ 9\end{bmatrix}\notin C\left(\begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\end{bmatrix}\right) = \text{span}\left\{\begin{bmatrix} 1\\ 1\\ 1\\ 1\end{bmatrix},\begin{bmatrix} 1\\ 2\\ 3\\ 4\end{bmatrix}\right\}\]
Note that if \(b\) is in the above column space, then
\[b = \begin{bmatrix} c+d\\ c+2d\\ c+3d\\ c+4d\end{bmatrix}\quad\Leftrightarrow\quad b=\begin{bmatrix} b_{1}\\ b_{2}\\ b_{3}\\ b_{4}\end{bmatrix} \text{ such that \(b_{j+1}-b_{j}\) is constant}\]
What to do if we are given an equation \(Ax=b\) that has no solution.
Note that a least squares solution to \(Ax=b\) is not necessarily a solution to \(Ax=b\).
How do we do this?
Find the vector \(\hat{b}\in C(A)\) which is closest to \(b\).
The equation \(Ax=\hat{b}\) has a solution.
A vector \(\hat{x}\) such that \(A\hat{x}=\hat{b}\) is called a least squares solution to \(Ax=b\).
We would like to find the vector \(x\) so that \(Ax\) is as close as possible to \(b\).
Proposition 2. If \(P\) is the orthogonal projection onto \(V\), and \(v\in V\), then \(v\cdot (w-Pw)=0\) for all \(w\in\R^{n}\).
Proof. Let \(w\in\R^{n}\), then we calculate
\[v\cdot (w-Pw) = v^{\top}(w-Pw)=(Pv)^{\top}(w-Pw) = v^{\top}Pw-v^{\top}PPw = 0.\]
Proposition 1. If \(P\) is the orthogonal projection onto \(V\), then \(P^2=P\) and \(P^{\top}=P\).
Proof. To show that \(P^2=P\), it is enough to check that \(P^{2}w=Pw\) for all \(w\in\R^{n}\). Note that \(Pw\in V\), and hence \(P^{2}w=P(Pw)=Pw\).
Let \(\{e_{1},\ldots,e_{k}\}\) be an orthonormal basis for \(V\) (this exists by the Gram-Schmidt orthogonalization procedure). Let \(A\) be a matrix with columns \(\{e_{1},\ldots,e_{k}\}\). Then, \(P=AA^{\top}\), and we have
\[P^{\top} = (AA^{\top})^{\top} = (A^{\top})^{\top}A^{\top} = AA^{\top} = P.\]
\(\Box\)
\(\Box\)
Proposition 3. If \(V\) is a subspace, and \(P\) and \(Q\) are both orthogonal projections onto \(V\), then \(P=Q\).
Proof. Assume toward a contradiction that there is some vector \(w\) such that \(Pw\neq Qw\), that is, \(Pw-Qw\neq 0\). Let \(v\in V\), then we have
\((Pw-Qw)\cdot v = (Pw)\cdot v - (Qw\cdot v) = (Pw)^{\top}v - (Qw)^{\top}v \)
\(\Box\)
\[= w^{\top}P^{\top}v - w^{\top}Q^{\top}v= w^{\top}Pv - w^{\top}Qv = w^{\top}v - w^{\top}v=0\]
This shows that \(Pw-Qw\) is orthogonal to any \(v\in V\). However, \(Pw-Qw\in V\), and thus
\[0 = (Pw-Qw)\cdot (Pw-Qw)\]
However, this implies that \(Pw-Qw=0\) \(\Rightarrow\Leftarrow\)
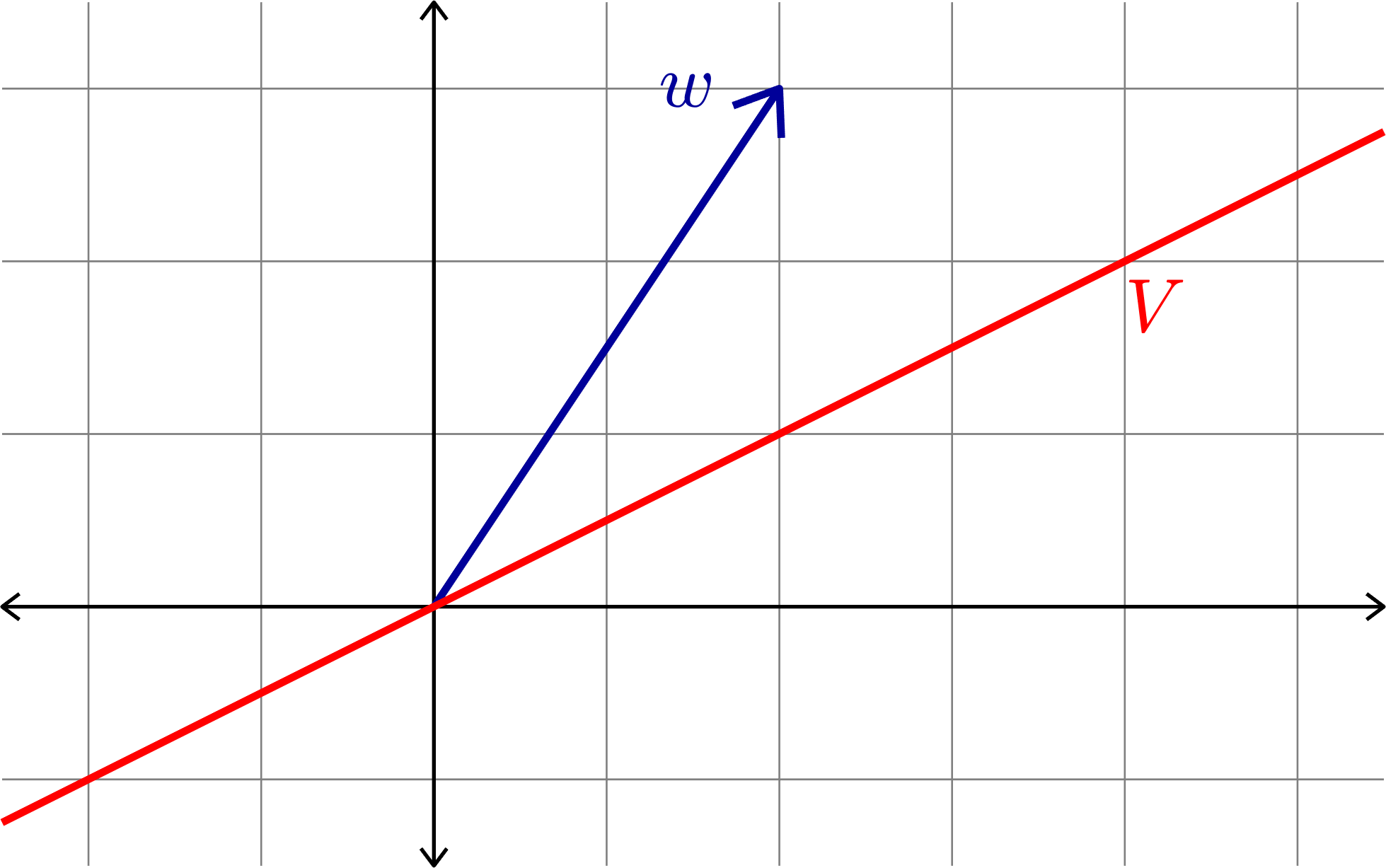
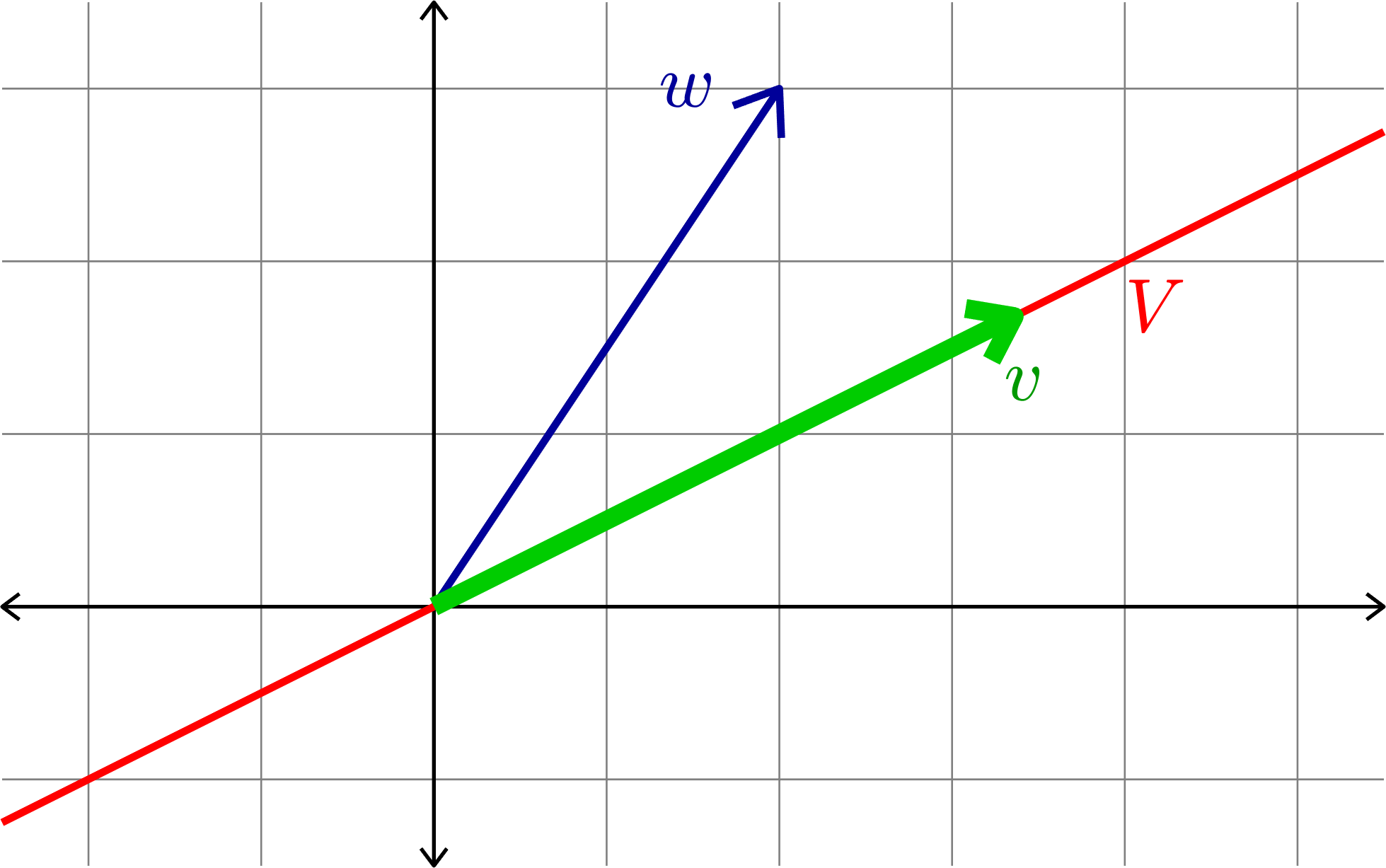
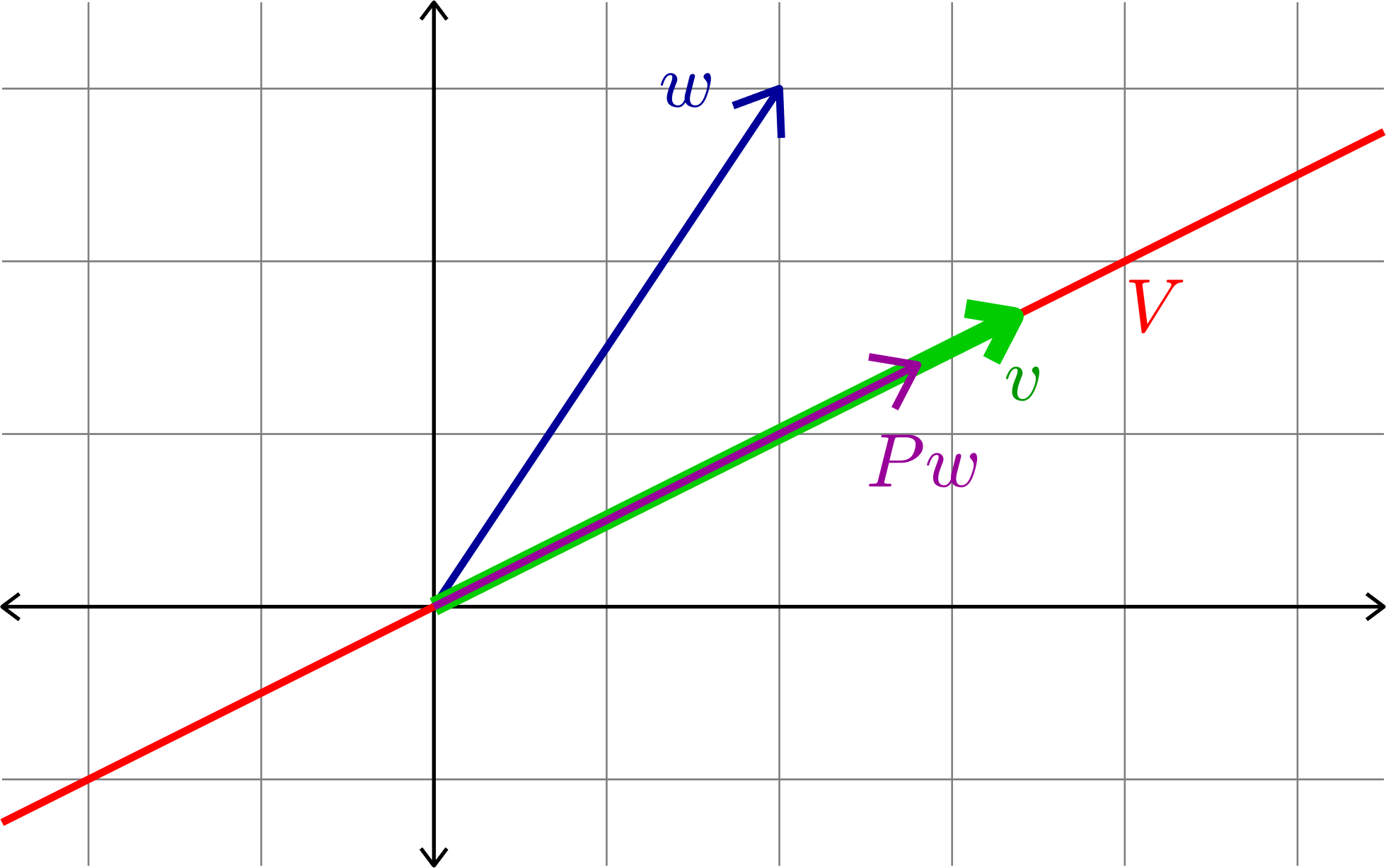
Theorem. (The Projection Theorem) If \(V\) is a subspace of \(\R^{n}\), \(w\in\R^{n}\), and \(P\) is the orthogonal projection onto \(V\), then
\[\|w-Pw\|\leq \|w-v\| \quad\text{ for all }v\in V.\]
Proof. By Proposition 2 we see that \(w-Pw\) is orthogonal to \(v\) for every \(v\in V\), and hence orthogonal to \(Pw-v\) for all \(v\in V\). By the Pythagorean Theorem we have
\[\|w-Pw\|^{2} + \|Pw-v\|^{2} = \|w-v\|^{2}.\]
This implies the theorem.
\(\Box\)
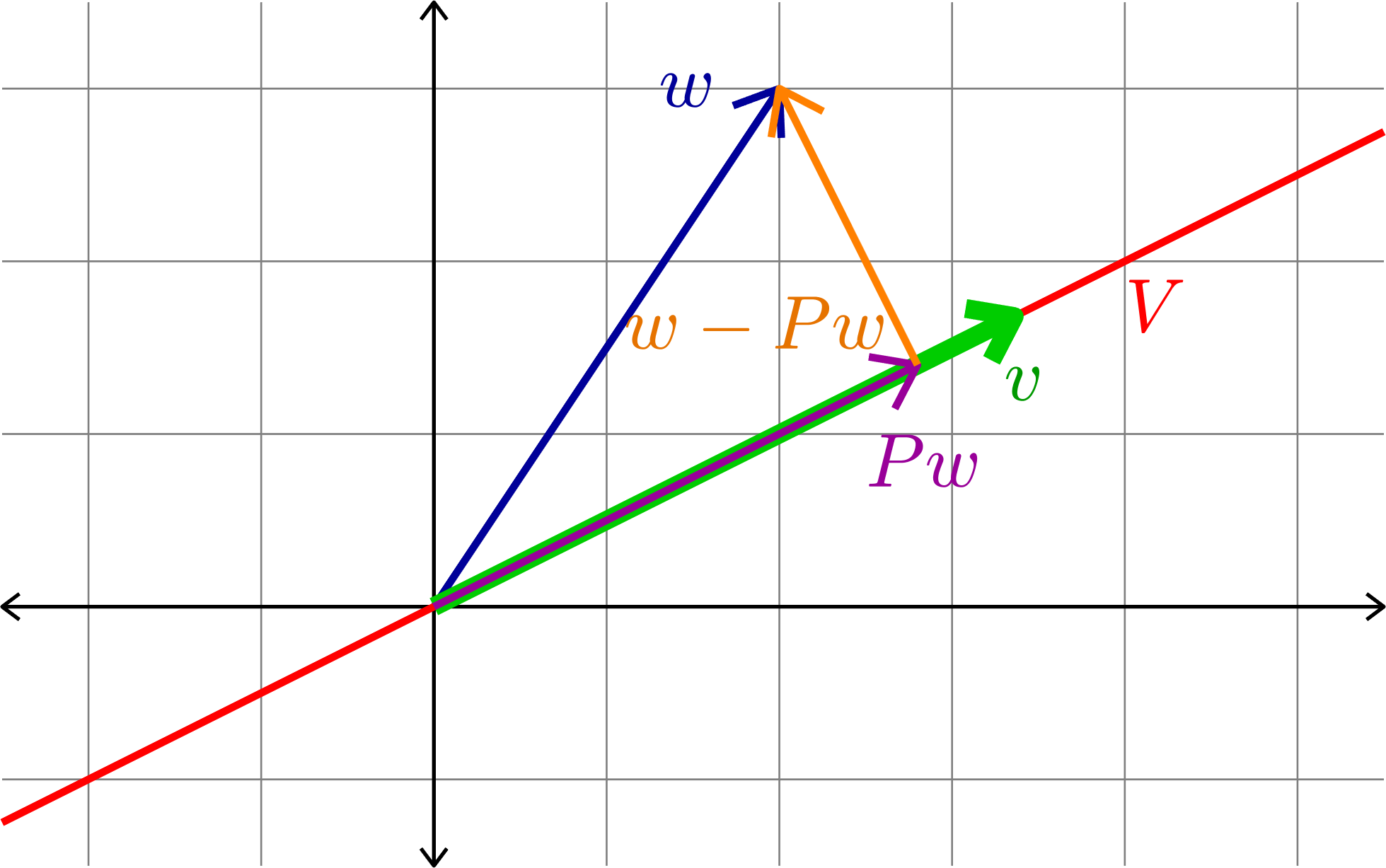
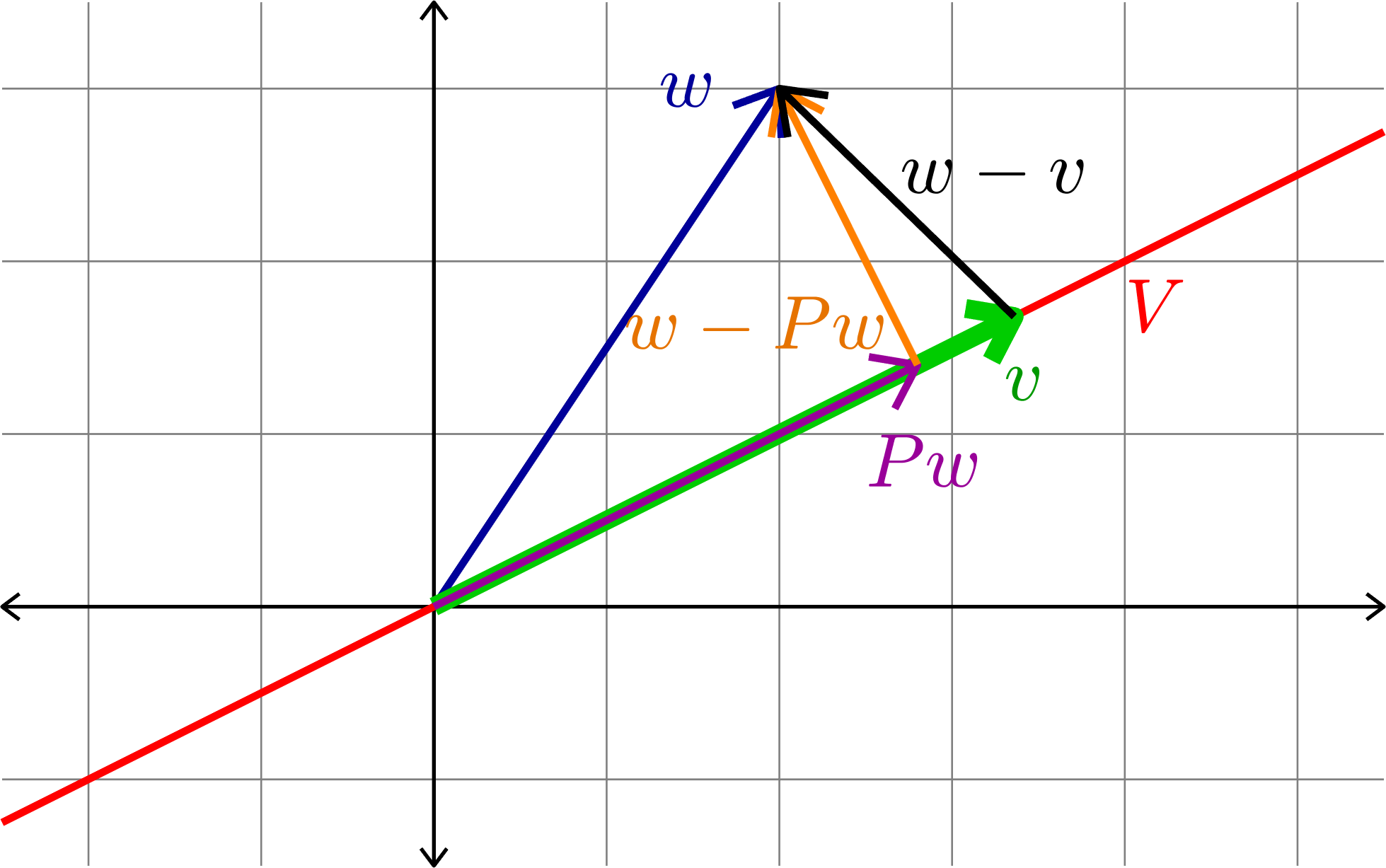
Notice that \(\|x-y\|\) is the distance between \(x\) and \(y\).
This theorem says that \(Pw\) is the closest point to \(w\) in the subspace \(V\).
What to do if we are given an equation \(Ax=b\) that has no solution.
By the Projection Theorem, if \(P\) is the projection onto \(C(A)\), then \(Pb\) is the closest vector in \(C(A)\) to \(b\).
Since \(Pb\in C(A)\), the equation \(Ax=Pb\) has a solution.
A solution to \(Ax=Pb\) is a least squares solution.
Closest linear data:
Hence, "linear" data is just vectors in \(C(L)\) where
\[L = \begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ \vdots & \vdots\\ 1 & n\end{bmatrix}\]
Closest linear data:
The data seems to be close to "linear."
What is linear data? We would say that the data
\[y=\begin{bmatrix} y_{1} & y_{2} & y_{3} & \cdots & y_{n}\end{bmatrix}^{\top}\]
is linear if \(y_{k+1}-y_{k}\) is the same number for all \(k\in\{1,\ldots,n-1\}\).
If \(y\) is linear, and \(m=y_{2}-y_{1}\) then we have
\[y=\begin{bmatrix} y_{1}\\ y_{2}\\ y_{3}\\ \vdots\\ y_{n}\end{bmatrix} = \begin{bmatrix} y_{1}\\ y_{1}+m\\ y_{1}+2m\\ \vdots\\ y_{1}+(n-1)m\end{bmatrix} = \begin{bmatrix} y_{0}+m\\ y_{0}+2m\\ y_{0}+3m\\ \vdots\\ y_{0}+nm\end{bmatrix} = y_{0}\begin{bmatrix} 1\\ 1\\ 1\\ \vdots\\ 1\end{bmatrix} + m\begin{bmatrix} 1\\ 2\\ 3\\ \vdots\\ n\end{bmatrix}\]
where \(y_{0} = y_{1}-m\).
Closest linear data:
Consider the following data \(y\). We want to find the closest "linear" data. That is, we want to find a vector \(\hat{y}\in C(L)\) so that \(\|y-\hat{y}\|\) is as small as possible. By the previous theorem, if \(P\) is the orthogonal projection onto \(C(L)\), then \(\hat{y} = Py\).
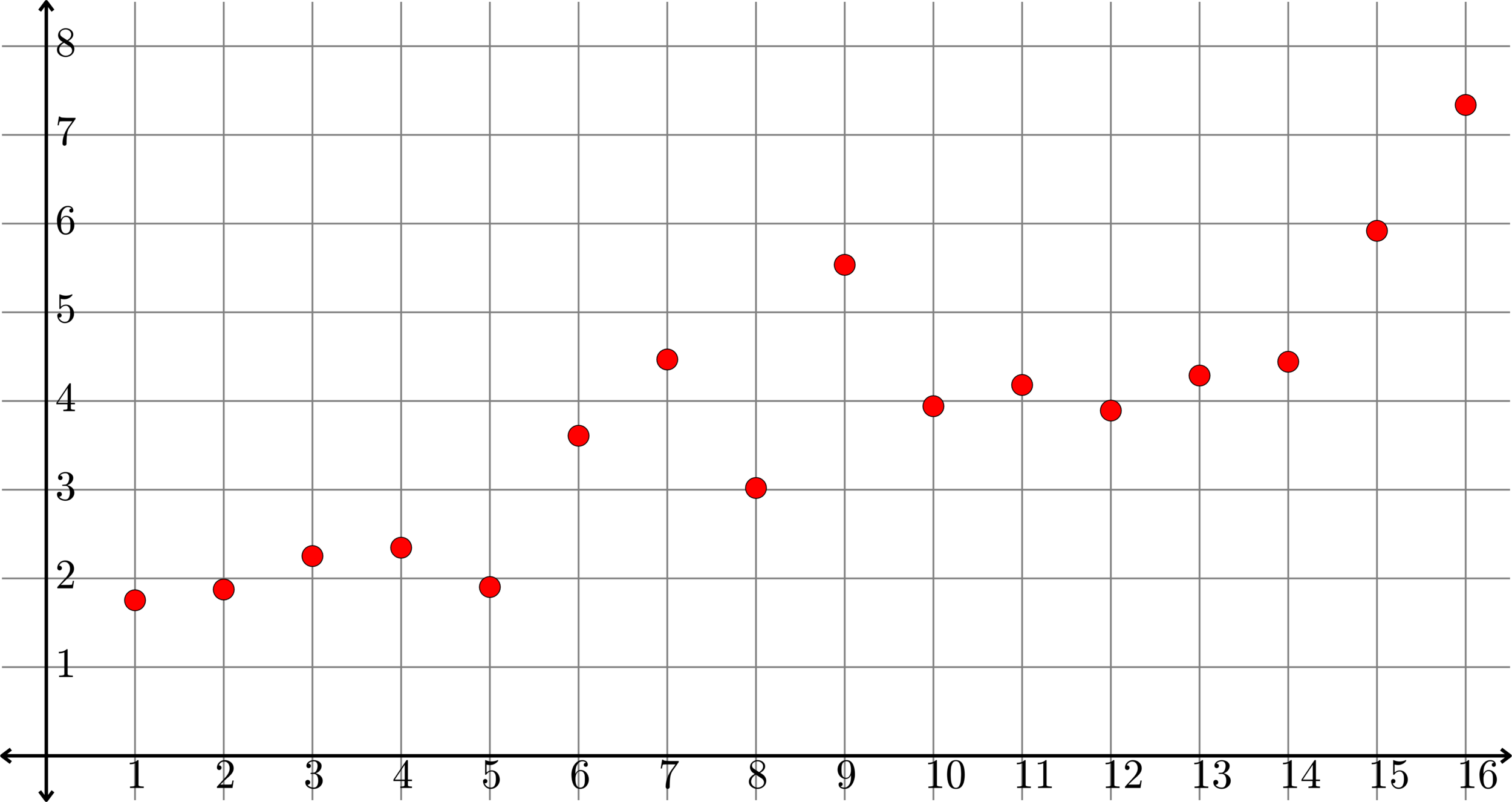

\(y=\)
We want to find the orthogonal projection onto \(C(L)\).
So, we will apply the Gram-Schmidt procedure to the columns of \(L\). Set \[e_{1} = \frac{1}{\sqrt{n}}\begin{bmatrix} 1\\ 1\\ 1\\ \vdots\\ 1\end{bmatrix}\]
\[=\begin{bmatrix} 1\\ 2\\ 3\\ \vdots\\ n\end{bmatrix} - \frac{n(n+1)}{2\sqrt{n}}\frac{1}{\sqrt{n}}\begin{bmatrix} 1\\ 1\\ 1\\ \vdots\\ 1\end{bmatrix} = \begin{bmatrix} 1\\ 2\\ 3\\ \vdots\\ n\end{bmatrix} - \frac{n+1}{2}\begin{bmatrix} 1\\ 1\\ 1\\ \vdots\\ 1\end{bmatrix} = \begin{bmatrix}1-\frac{n+1}{2}\\ 2-\frac{n+1}{2}\\ 3-\frac{n+1}{2}\\ \vdots\\ n-\frac{n+1}{2}\end{bmatrix}\]
\[w_{2} = \begin{bmatrix} 1\\ 2\\ 3\\ \vdots\\ n\end{bmatrix} - \left(\frac{1}{\sqrt{n}}\begin{bmatrix}1 & 1 & 1 & \cdots & 1\end{bmatrix}\begin{bmatrix}1\\ 2\\ 3\\ \vdots\\ n\end{bmatrix}\right)\frac{1}{\sqrt{n}}\begin{bmatrix} 1\\ 1\\ 1\\ \vdots\\ 1\end{bmatrix}\]
\[e_{2} = \frac{1}{\|w_{2}\|}w_{2}\]
\[ = \frac{1}{2}\begin{bmatrix}1-n\\ 3-n\\ 5-n\\ \vdots\\ 2n-1-n\end{bmatrix}\]
Example. \(n=16\)
\[e_{1} = \frac{1}{4}\begin{bmatrix}1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\end{bmatrix},\quad e_{2} = \frac{1}{\sqrt{1360}}\begin{bmatrix} -15\\ -13\\ -11\\ -9\\ -7\\ -5\\ -3\\ -1\\ 1\\ 3\\ 5\\ 7\\ 9\\ 11\\ 13\\ 15 \end{bmatrix}\]
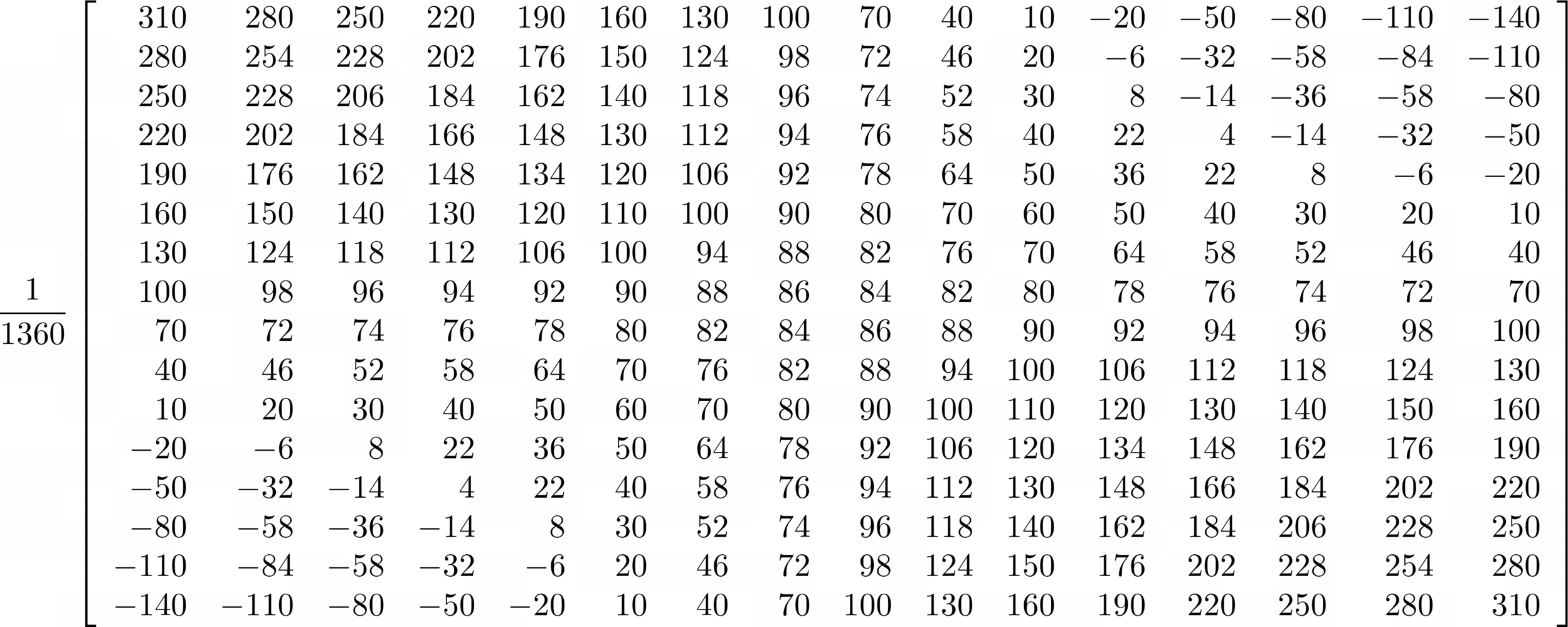
The Projection matrix:
\(P=\)


\(y=\)
\(Py=\)
If \(z\) is any other "linear" data, then \(\|y-z\|\geq \|y-Py\|\).
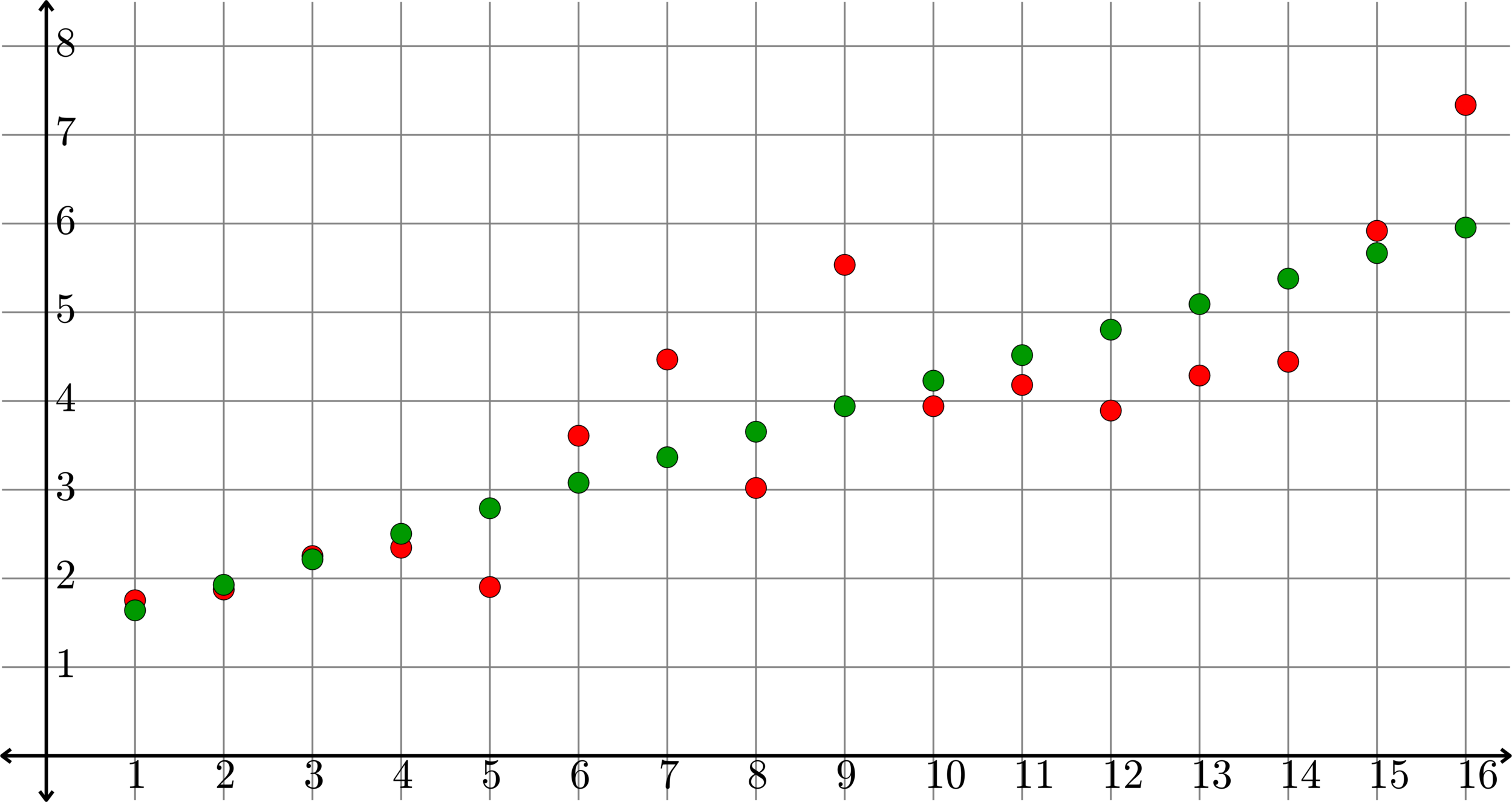
The vector \(y\) is plotted in red.
The vector \(Py\) is plotted in green.
We can solve \(Lx=Py\):
\[\begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ 1 & 4\\ 1 & 5\\ 1 & 6\\ 1 & 7\\ 1 & 8\\ 1 & 9\\ 1 & 10\\ 1 & 11\\ 1 & 12\\ 1 & 13\\ 1 & 14\\ 1 & 15\\ 1 & 16\end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\end{bmatrix} = \]

\(\Rightarrow x_{1} = 1.3523,\ \text{and}\ x_{2} = 0.2877\)
So, the best fit line to this data would be \(y=0.2877x+1.3523\)
Projections in Inner Product Spaces
Definition. Let \(V\) be an inner product space and let \(W\subset V\) be a subspace. A linear map \(P:V\to V\) is an orthogonal projection onto \(W\) if
- \(Pv\in W\) for all \(v\in V\)
- \(Pw=w\) for all \(w\in W\)
- \(\langle Pv,v-Pv\rangle = 0\) for all \(v\in V\).
Theorem. (The Projection Theorem) If \(V\) is an inner product space, \(W\subset V\) is a subspace, \(v\in V\), and \(P\) is the orthogonal projection onto \(W\), then
\[\|v-Pv\|\leq \|v-w\| \quad\text{ for all }w\in W.\]
Exercise: Prove the analogs of Propositions 1,2, and 3 for projection in general inner-product spaces.
Projections in Inner Product Spaces
Theorem. If \(V\) is an inner product space, and \(W\subset V\) is a subspace with orthonormal basis \(\{f_{1},f_{2},\ldots,f_{k}\}\), then the map \(P:V\to V\) given by
\[Pv = \sum_{i=1}^{k}\langle v,f_{i}\rangle f_{i}\]
is the orthogonal projection onto \(W\).
Proof. Exercise.
Example. Consider the inner product space \(\mathbb{P}_{2}\) with inner product
\[\langle f(x),g(x)\rangle = \int_{-1}^{1}f(x)g(x)\,dx.\]
We wish to find the element of the subspace \(\mathbb{P}_{1}\subset \mathbb{P}_{2}\) that is closest to the polynomial \(x^2-2x\).
To do this, we need to find the projection onto \(\mathbb{P}_{1}\), and hence we need an orthonormal basis for \(\mathbb{P}_{1}\).
Since \[\langle 1,x\rangle = \int_{-1}^{1}x\,dx = 0\] we see that \(\{1,x\}\) is an orthogonal basis for \(\mathbb{P}_{1}.\) If we normalize, then see that \(\{f_{1},f_{2}\}\), where \[f_{1} = \frac{1}{\sqrt{2}}\quad\text{and}\quad f_{2}(x) = \sqrt{\frac{3}{2}}x\] is an orthonormal basis.
Projections in Inner Product Spaces
Example. By the previous theorem \(P:\mathbb{P}_{2}\to\mathbb{P}_{2}\) given by
\[P(f(x)) = \langle f(x),f_{1}(x)\rangle f_{1}(x) + \langle f(x),f_{2}(x)\rangle f_{2}(x)\] is the orthogonal projection onto \(\mathbb{P}_{1}\).
By the Projection Theorem
\[P(x^2-2x) = \langle x^2-2x,\tfrac{1}{\sqrt{2}}\rangle \tfrac{1}{\sqrt{2}} + \langle x^2-2x,\sqrt{\tfrac{3}{2}}x\rangle \sqrt{\tfrac{3}{2}}x\]
Projections in Inner Product Spaces
\[= \tfrac{1}{2}\langle x^2-2x,1\rangle 1 + \tfrac{3}{2}\langle x^2-2x,x\rangle x\]
is the closest point in \(\mathbb{P}_{1}\) to the polynomial \(x^2-2x\). Note that, "closest" here means that \(\|x^2-2x-f(x)\|\) is as small as possible for all \(f(x)\in\mathbb{P}_{1}\).
\[\langle x^2-2x,1\rangle = \int_{-1}^{1}x^2-2x\,dx = \frac{2}{3}\]
\[\langle x^2-2x,x\rangle = \int_{-1}^{1}(x^2-2x)x\,dx = -\frac{4}{3}\]
Hence \(P(x^2-2x) = \frac{1}{3} - 2x\).
Example. The function \(x^2-2x\) is graphed in blue. The closest linear polynomial \(-2x+\frac{1}{3}\) is graphed in red.
Projections in Inner Product Spaces

Linear Algebra Day 19
By John Jasper
Linear Algebra Day 19
- 917



