Theory of NP-Completeness

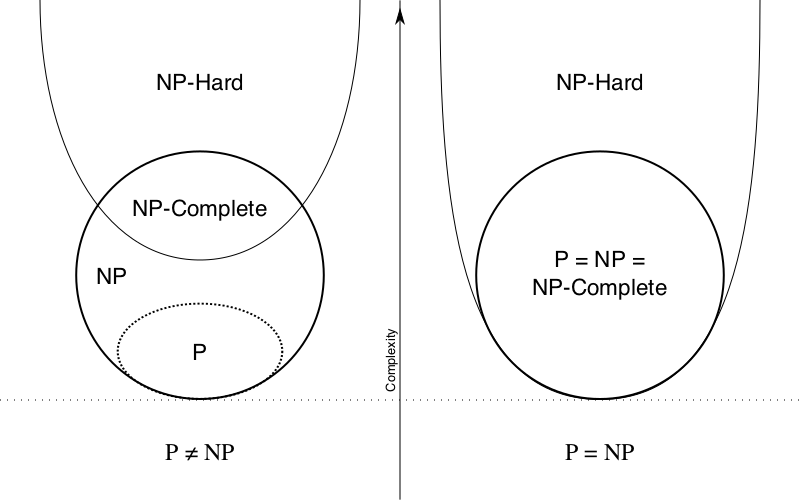
Definitions:

• P - deterministic polynomial-time decision problems
• NP - non-deterministic turing machine problems that can be verified in polynomial-time.
• NP-Hard - at least as hard as the hardest problems in NP.

Theory of NP-Completeness

NP-Complete:

• A decision problem D is
  NP-complete if:

  • D is in NP, and
  • Every problem in NP is reducible to D in polynomial time

Proof

Approach:

 

• We transform Exact Cover by 3-Sets to Partition into Triangles

• Polynomial time transformation using local replacement.

Local Replacement:

• Pick some aspect of the know NP-Complete problem instance to make up a collection of basic units.
• We obtain the corresponding instance of the target problem by replacing each basic unit in a uniform way with a different structure.
• ​The key point is that each replacement constituted only local modification of structure.

Proof

• Let the set X with |X| = 3q and the collection C of 3 element subsets of X be an arbitrary instance of Exact Cover by 3 Sets.

• We shall construct a graph G=(V,E), with |V|=3q', such that the desired partition exists for G if and only if C contains exact cover. 

Proof:

Proof

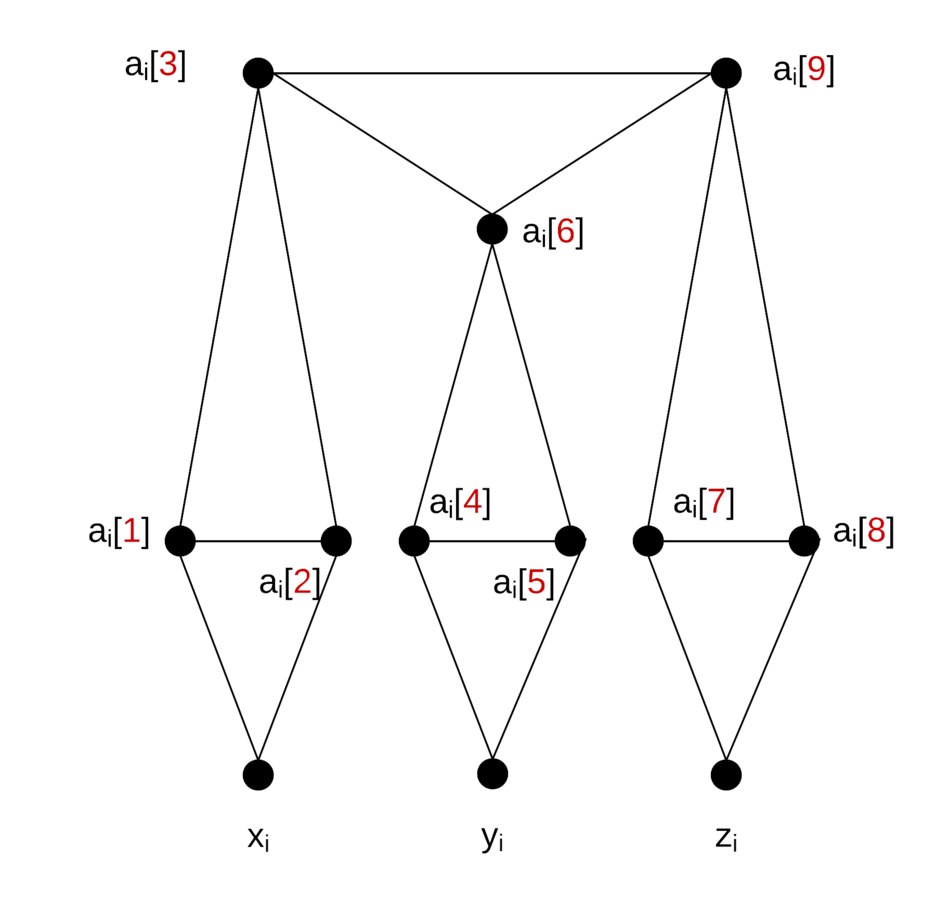
• The basic units of the Exact Cover by 3 Sets instance are the 3-element subsets in C.

 

• The local replacement substitutes for each such subset c_i = { x_i , y_i , z_i } ∈ C the collection E_i of 18 edges shown in the figure below:

Proof:

Proof

• The only vertices that appear in edges belonging to more than a single E_i are those that are in the set X.

• |V|  =  |X| + 9 |C|  =  3q + 9 |C|   so that q' = q + 3 |C| and is therefore an instance of Partition into Triangles.

Proof:

Proof

• If  c₁, c₂, ... , c_q are the 3 element subsets from C in any EXACT COVER for X, then the corresponding partition  V = V1 U V2 U ... U Vq' is given by taking

 

{a_i[1], a_i[2], x_i},  {a_i[4], a_i[5], y_i}

{a_i[7], a_i[8], z_i},  {a_i[3], a_i[6], a_i[9] }

 

from the vertices meeting E_i wherever c_i = { x_i , y_i , z_i } IS in the exact cover, and by taking:

 

{a_i[3], a_i[6], a_i[9]},  {a_i[3], a_i[6], a_i[9]},  {a_i[3], a_i[6], a_i[9]} 

 

from the vertices meeting E_i whenever c_i IS NOT in the exact cover.

 

Proof:

Proof

• Let us say that it was  {a_i[1], a_i[2], x_i}

• Then  {a_i[4], a_i[5], y_i}{a_i[7], a_i[8], z_i},  and {a_i[3], a_i[6], a_i[9] }

   

  must also be in the triangle partition. 

Proof:

Proof

• Therefore each x appears in exactly one chosen c_i

Proof:

• This also implies that we choose exactly q c_i elements of C.

• We have shown that G can be partitioned into
  q' = q + |C| triangles if and only if  C contains an exact cover of q sets for X.