Average Ehrhart coefficients & symplectic Hecke eigenbases
Joshua Maglione
Polytopes
A polytope is the convex hull of finitely many points in \(\mathbf{R}^n\).
A lattice polytope is the convex hull of finitely many points in \(\mathbf{Z}^n\subset \mathbf{R}^n\).
For us: "polytope" means "lattice polytope"
Discrete Volumes
For a polytope \(P\) and \(k\in \mathbf{Z}_{\geqslant 0}\) the \(k\)th dilate is \(kP = \{k\cdot p ~|~ p \in P\}\)
The discrete volume of a polytope \(P\) is \(\# (P\cap \mathbf{Z}^n)\).
\lim_{k\to \infty} \dfrac{\#(kP\cap \mathbf{Z}^n)}{k^n} = \mathrm{vol}(P)
E_P : \mathbf{Z}_{\geqslant 0} \to \mathbf{Z}, \qquad k\mapsto \#(kP\cap\mathbf{Z}^n)
Corollary. The degree is \(\leqslant n\). The coefficient of \(t^n\) is \(\mathrm{vol}(P)\).
Ehrhart
polynomial
Ehrhart polynomials
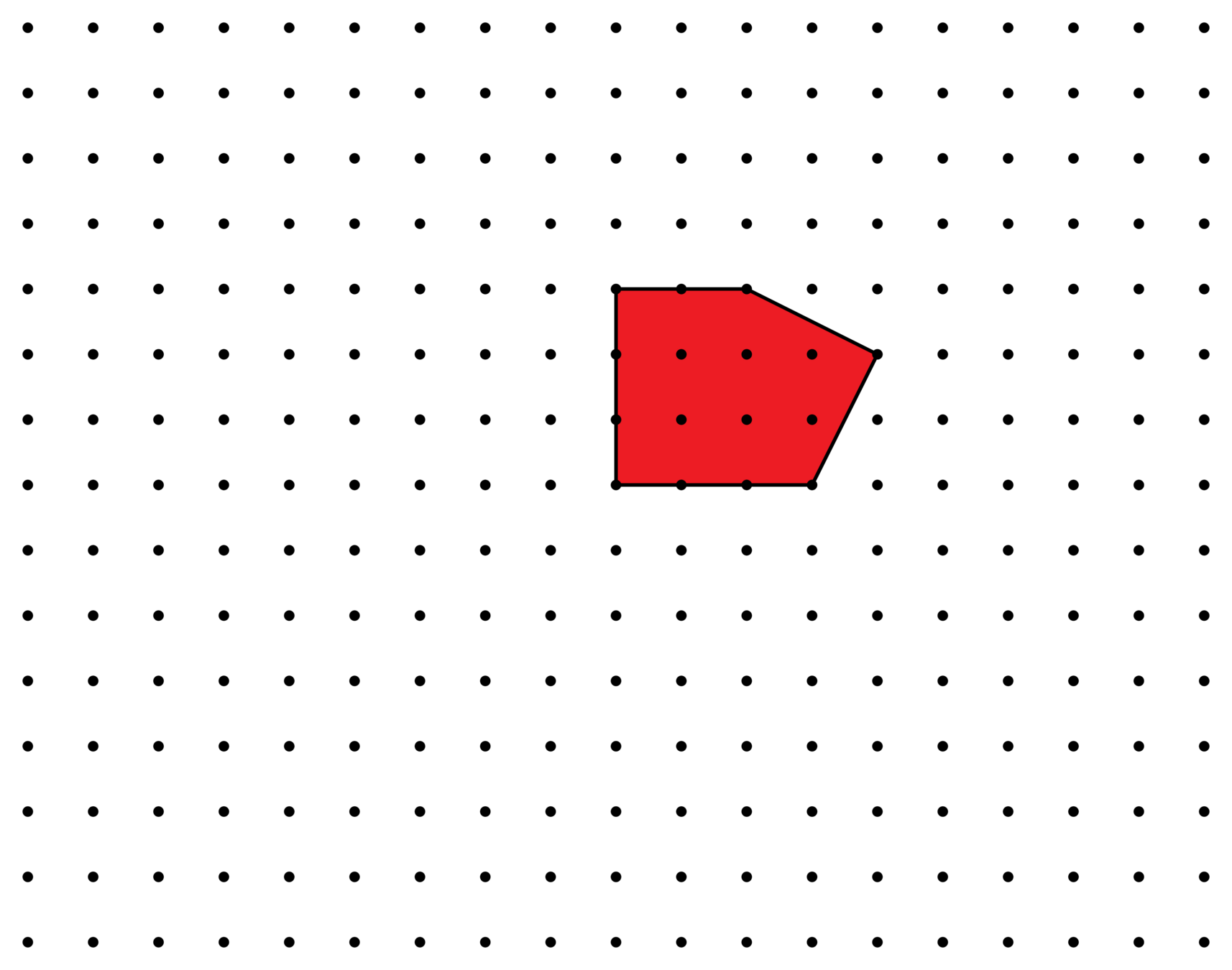
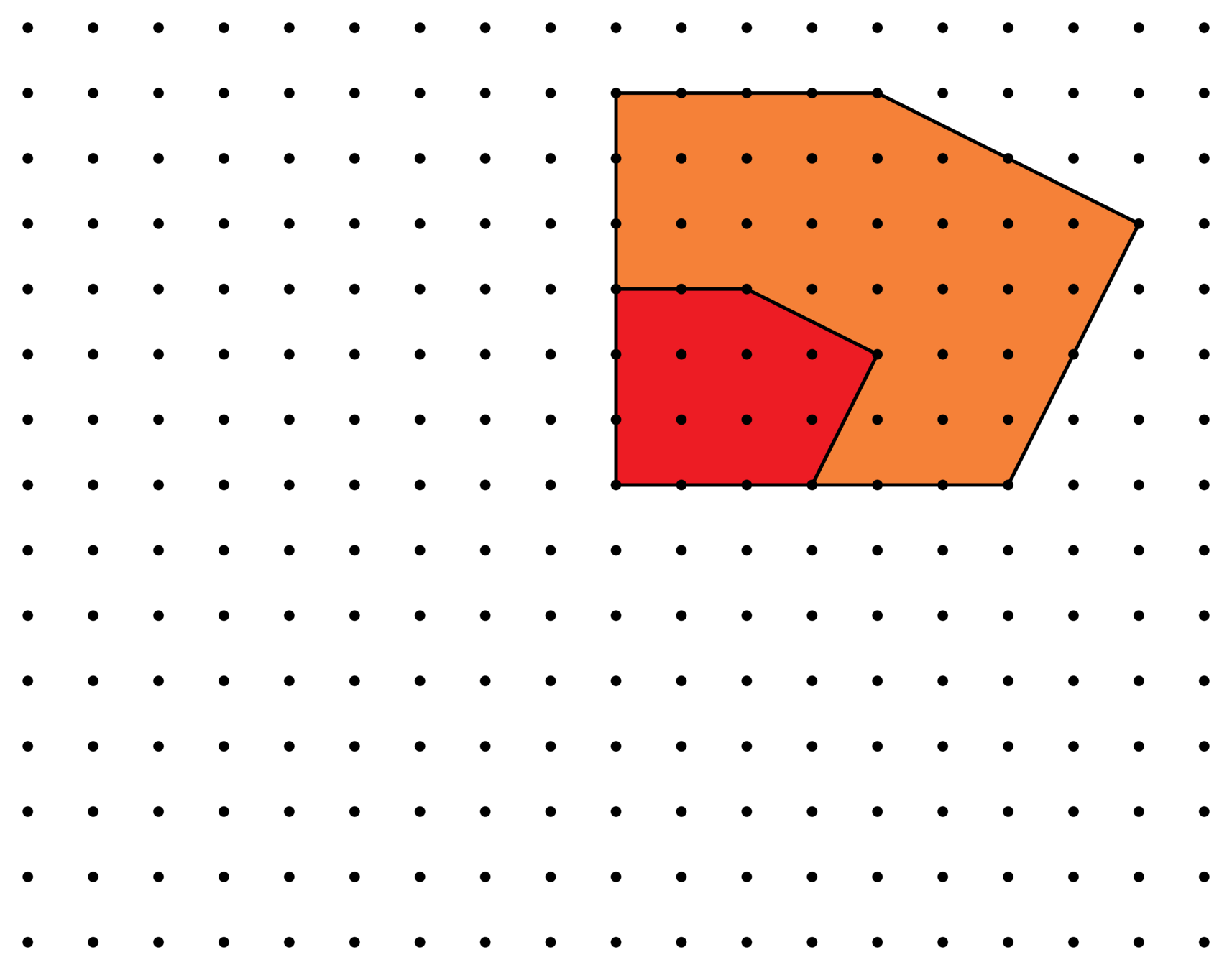
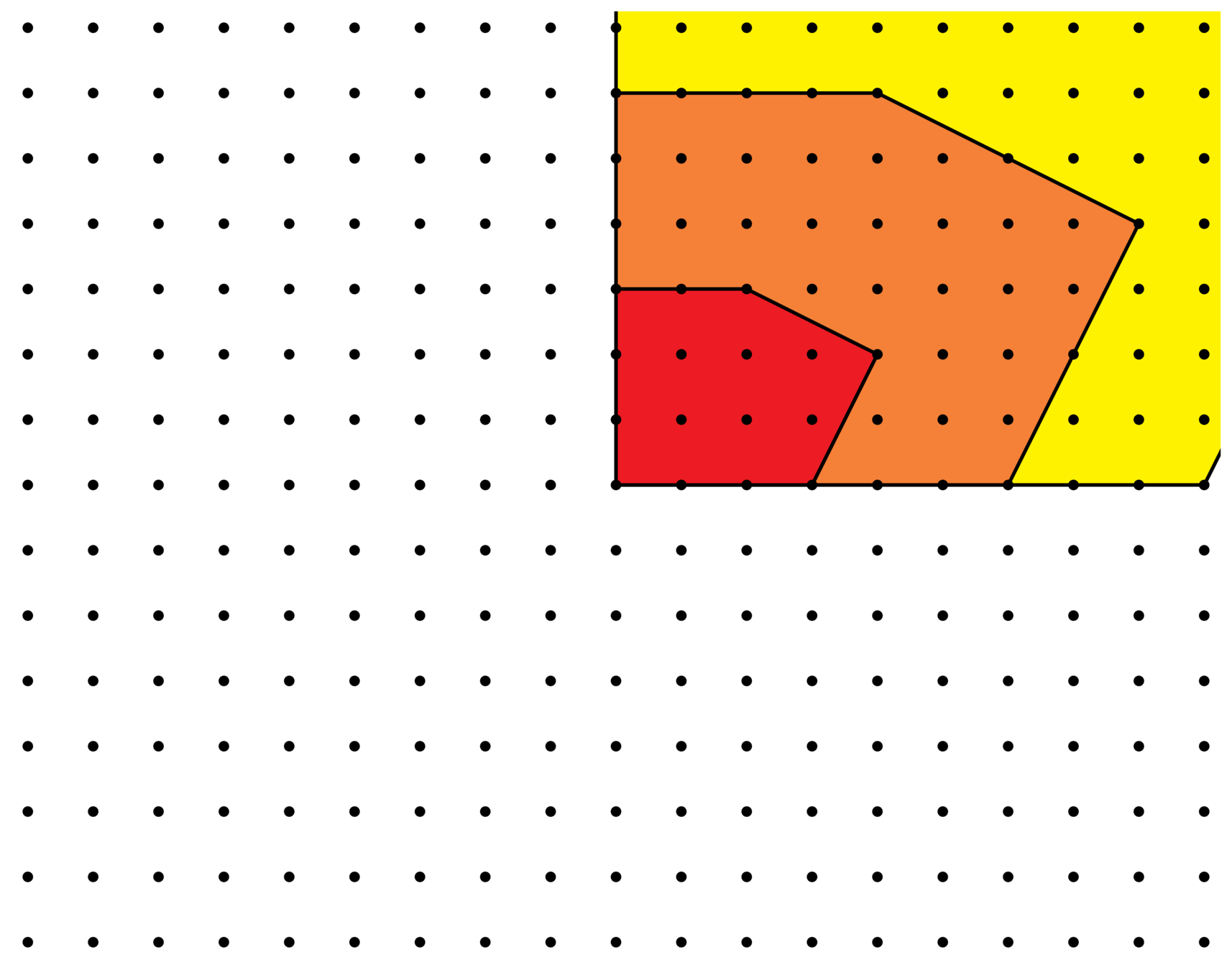
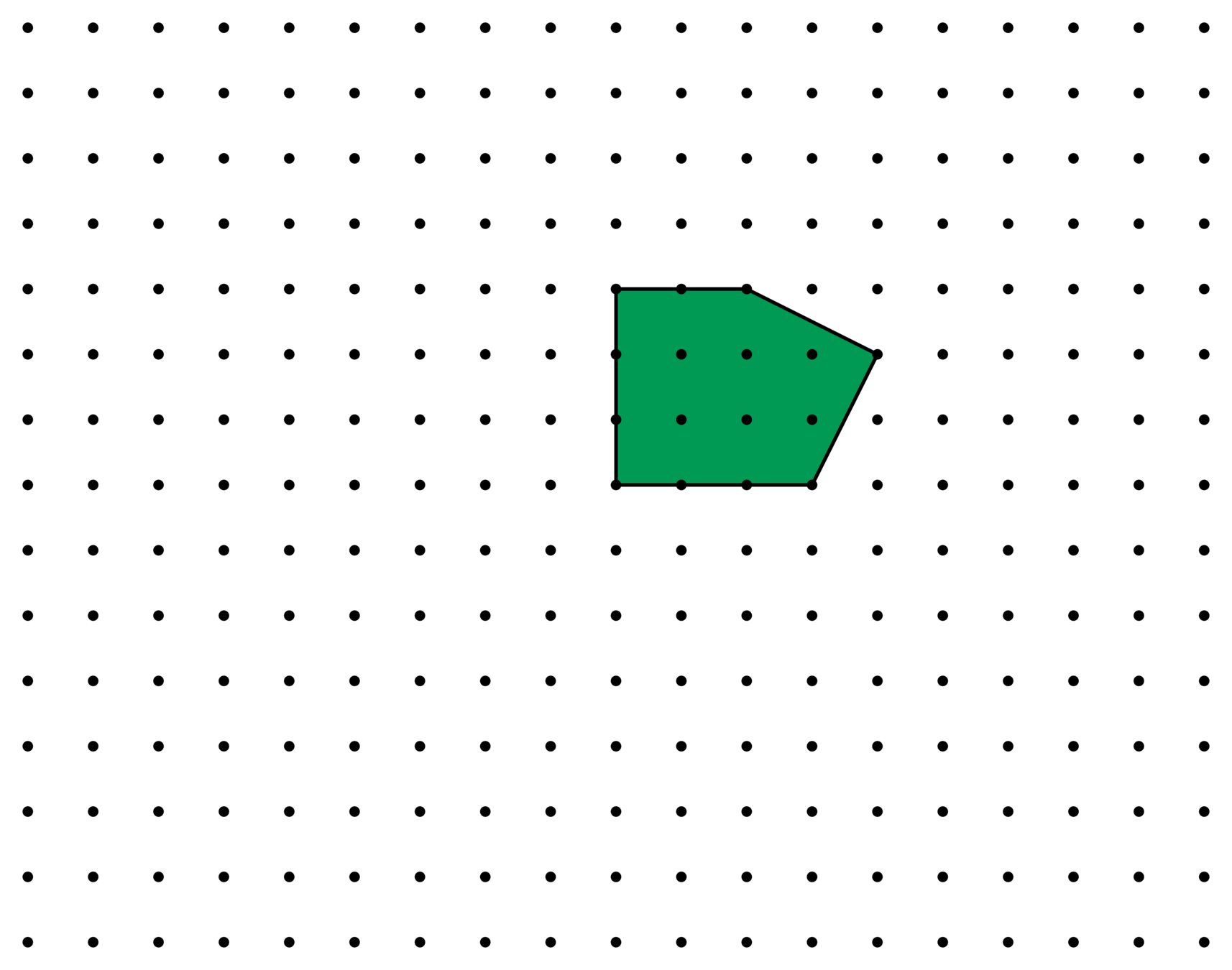
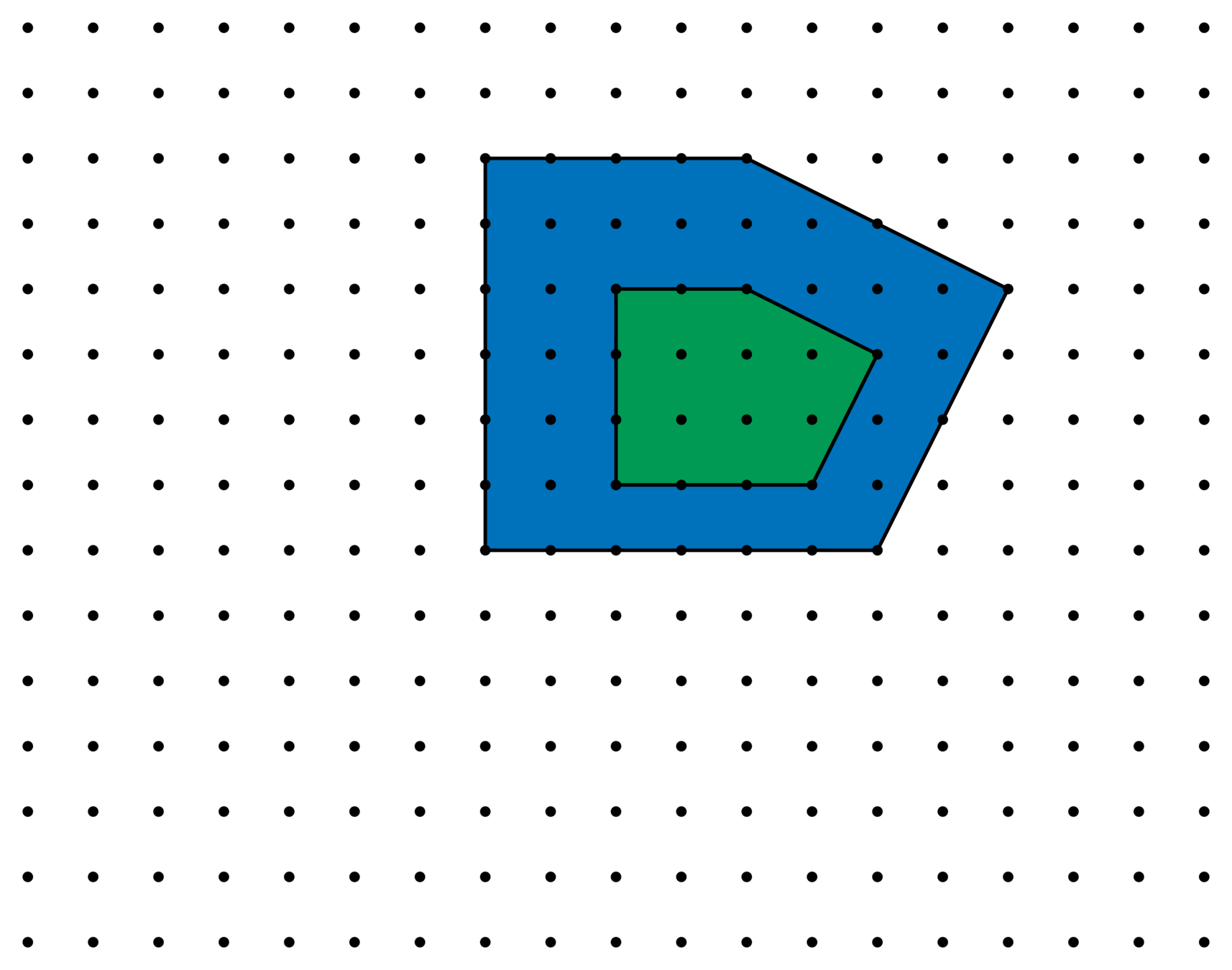
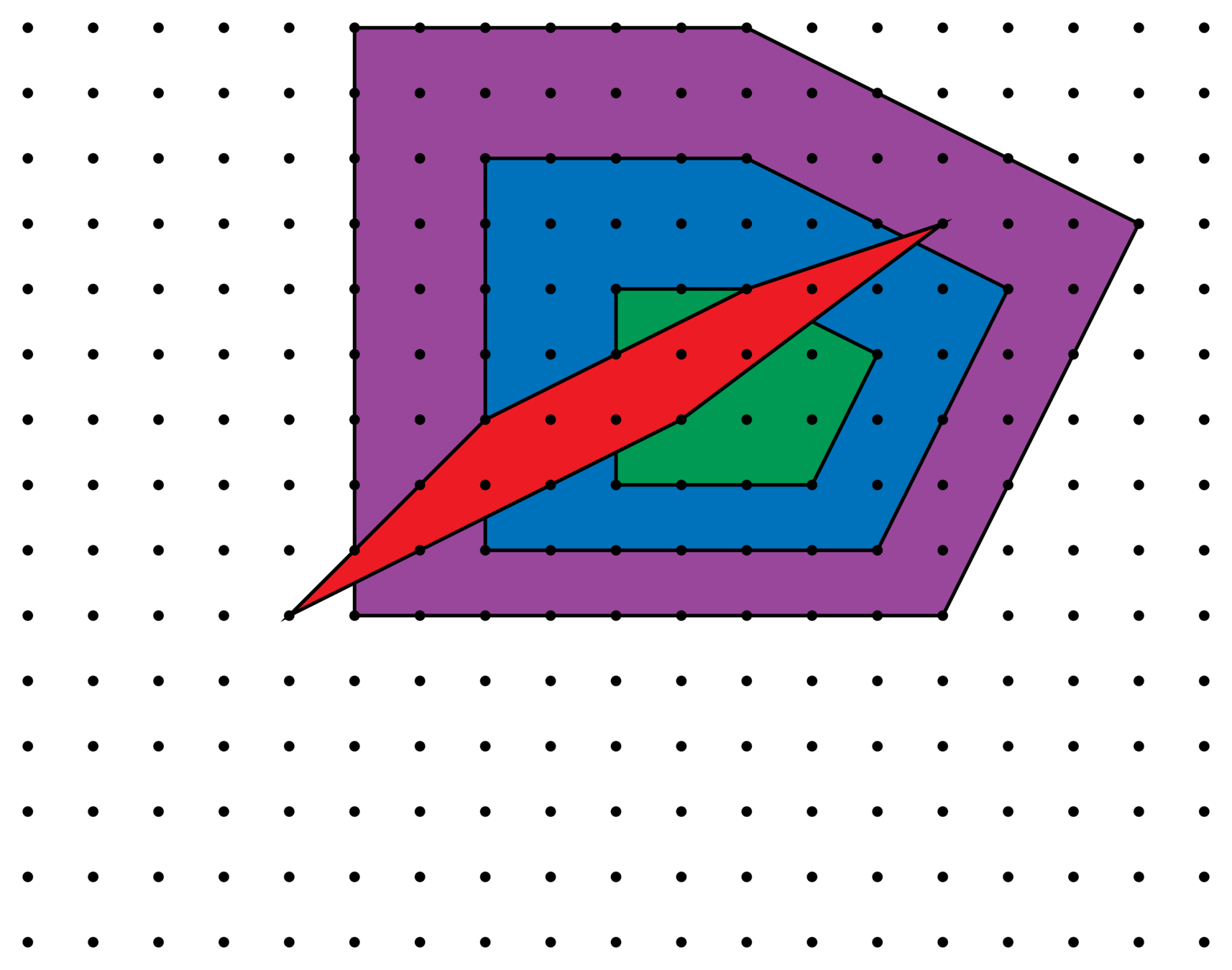
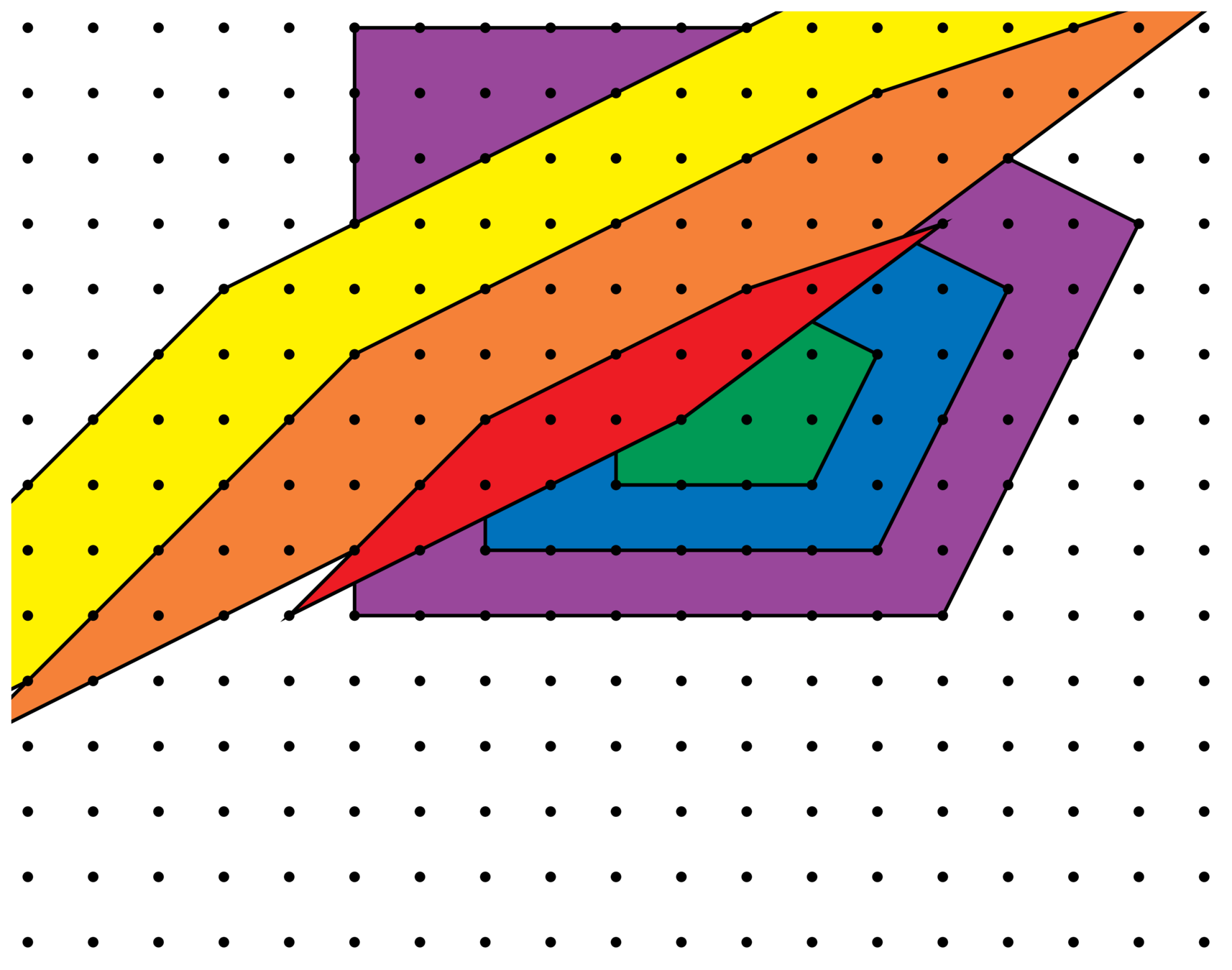
\(E(t) = 10t^2 + 5t + 1\)
\(E_P^{\Lambda}(t)\) : Ehrhart polynomial
\(t \mapsto \#(tP\cap \Lambda)\)
lattice: \(\Lambda = \mathbf{Z}^2\)
\(E(1)=16\)
\(E(3)=106\)
\(E(2)=51\)
Other coefficients with meaning?
Let \(E_P^{\Lambda}(t) = c_0 + c_1t + \cdots + c_nt^n\). For \(\ell\in \{0,\dots, n\}=[n]_0\), define
\mathscr{E}_{n, \ell}^{\Lambda}(P) = c_{\ell}.
Thus, \(\mathscr{E}_{n,\ell}^{\Lambda}\) is the function on polytopes in \(\mathbf{R}^n\) extracting the \(\ell\)th coefficient of its Ehrhart polynomial.
More
complicated
\begin{aligned}
\mathscr{E}_{n,n} &= \mathrm{vol} \\
\mathscr{E}_{n,n-1} &= \frac{1}{2}\mathrm{vol}_{\partial} \\
&~~\vdots \\
\mathscr{E}_{n,0} &= 1
\end{aligned}
\Lambda = \mathbf{Z}^n
Example: \((a,b,c)\)-simplex
\mathscr{E}_{3,0}(P) = 1 \qquad \mathscr{E}_{3,2}(P) = \frac{ab+bc+ca+1}{4} \qquad \mathscr{E}_{3,3}(P) = \frac{abc}{6}
(0,0,0)
(0,0,0)
(0,0,c)
(0,b,0)
(a,0,0)
P =
\((a,b,c)\) co-prime
Here, \(S\) is a Dedekind sum. With
\mathscr{E}_{3,1}(P) = \frac{1}{12}\left(\frac{ab}{c} + \frac{bc}{a} + \frac{ca}{b} + \frac{1}{abc} + 3(a+b+c) + 9\right) - S
s(p, q) = \sum_{i=1}^q \left(\left(\frac{i}{q}\right)\right) \left(\left(\frac{pi}{q}\right)\right)
((x)) = \begin{cases}
0 & x\in \mathbf{Z}, \\
x - \lfloor x\rfloor -1/2 & x\not\in \mathbf{Z},
\end{cases}
S = s(ab, c) + s(bc, a) + s(ca, b)
Brion & Vergne (1997) proved that \(\mathscr{E}_{n,\ell}\) are given by certain differential Todd operators acting on \(\mathrm{vol}\) for simple polytopes.
\mathrm{Todd}(z) = \dfrac{z}{1 - \mathrm{exp}(-z)} = 1 + \frac{1}{2}z + \sum_{k=1}^{\infty}(-1)^{k-1}\dfrac{B_{2k}}{(2k)!}z^{2k}
Unimodular invariant valuations
An \(\mathbf{R}\)-valued function \(\varphi\) on polytopes is a valuation if
\varphi(P) + \varphi(Q) = \varphi(P\cup Q) + \varphi(P\cap Q)
whenever \(P, Q, P\cap Q, P\cup Q\) are polytopes and \(\varphi(\varnothing)=0\).
A valuation \(\varphi\) is unimodular invariant if for all \(\alpha\in \mathrm{Aut}(\Lambda)\!\leqslant\! \mathrm{Aff}_{n}(\mathbf{R})\)
\varphi = \varphi\alpha.
Valuations capture
"geometric" measurements
Examples:
- Volume
- Surface area
- Mean width
- Euler characteristic
is a basis for the space of unimodular invariant valuations.
\left\{\mathscr{E}_{n,0},\; \mathscr{E}_{n,1},\; \dots,\; \mathscr{E}_{n,n}\right\}
Theorem (Betke & Kneser (1985)). The set
The Ehrhart coefficients encode all geometric measurements.
Betke & Kneser is a discrete analogue of Hadwiger's Theorem (1957).
The analogy, unfortunately, does not carry over to the properties of the valuations \(\mathscr{E}_{n,\ell}\).
The \(n+1\) intrinsic volumes are a basis for the space of certain valuations on compact convex bodies in \(\mathbf{R}^n\).
\sum_{m=0}^{\infty} E_P(m) t^m = \dfrac{h^*_0(P) + h^*_1(P)t + \cdots + h^*_n(P)t^n}{(1 - t)^{n+1}}
We can form the Ehrhart series:
Ehrhart series & \(h^*\)-polynomial
The \(h_i^*\) are unimodular invariant but not valuations.
Stanley (1980) proved non-negativity:
\begin{aligned}
h_0^*(P) &= 1, & h_k^*(P) &\in \mathbf{Z}_{\geqslant 0}
\end{aligned}
and, in (1993), monotonicity:
P\subseteq Q \implies \forall i,\ h_i^*(P)\leqslant h_i^*(Q)
Is there anything special about Ehrhart coefficients?
\sum_{i=0}^n{\color{blue}\mathscr{E}_{n,i}(P)}t^i = \sum_{i=0}^n {\color{blue}h_i^*(P)} \binom{t + n - i}{n} = \sum_{i=0}^n {\color{blue}f_i^*(P)} \binom{t - 1}{i}
Breuer (2012) defined the \(f^*\)-polynomial writing Ehrhart polynomial in a different polynomial basis:
Jochemko & Sanyal (2018) proved that the \(f^*_i\) form the essentially unique basis for \(\mathrm{UIV}_n\) which are non-negative and monotone.
unimodular invariant
valuations
Unique* Hecke eigenfunctions
Theorem (Alfes, M, & Voll (2025)). The valuations
\{\mathscr{E}_{2n,0}, \mathscr{E}_{2n, 1}, \dots, \mathscr{E}_{2n, 2n}\}
form a symplectic Hecke eigenbasis for the space of \(\mathrm{UIV}_{2n}\).
Theorem (Gunnells & Rodriguez Villegas (2007)). The valuations
\{\mathscr{E}_{n,0}, \mathscr{E}_{n, 1}, \dots, \mathscr{E}_{n, n}\}
form a Hecke eigenbasis for the space of \(\mathrm{UIV}_n\).
Up to independent scaling, this is the unique basis of such valuations.
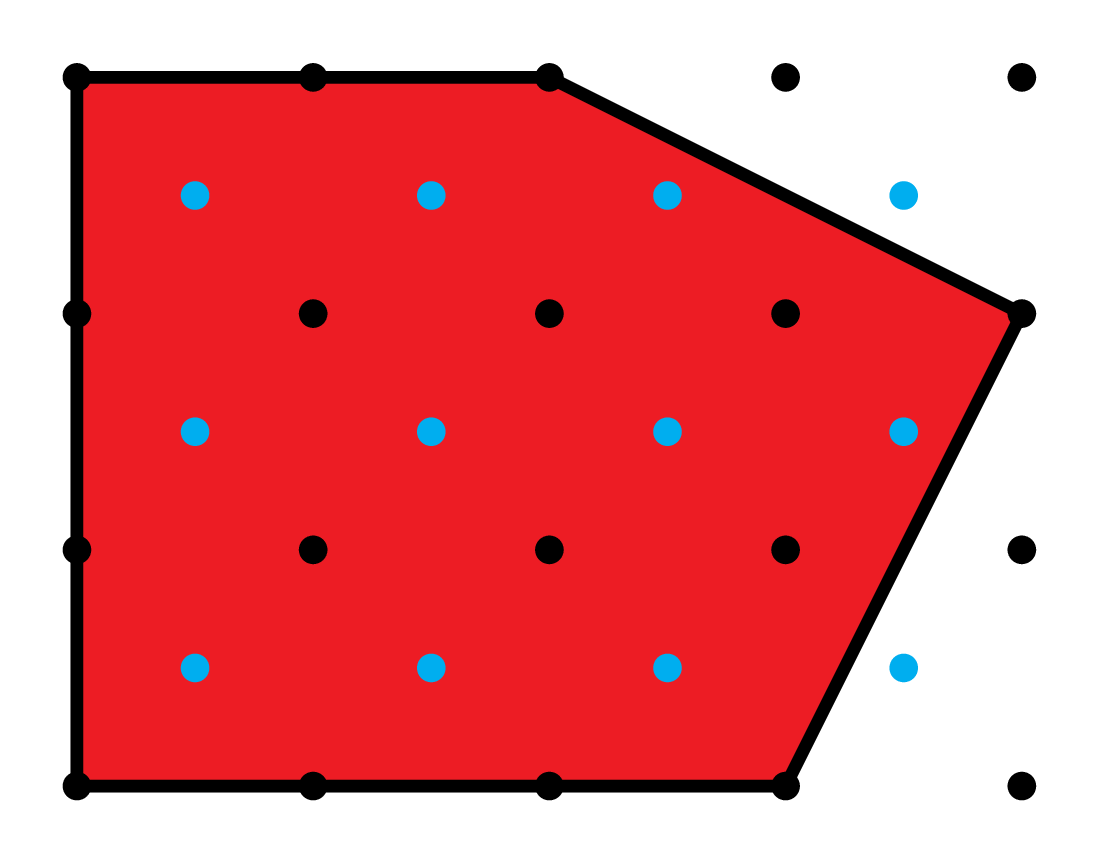
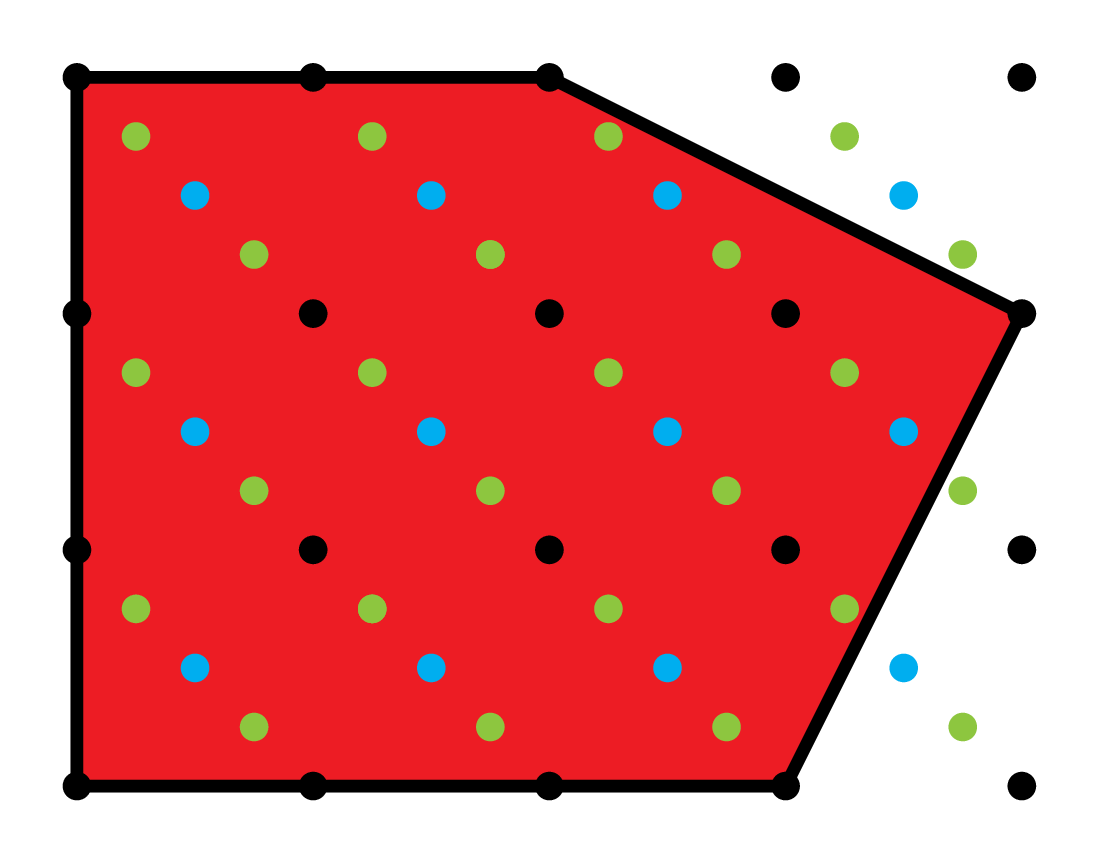
Lattice perspective
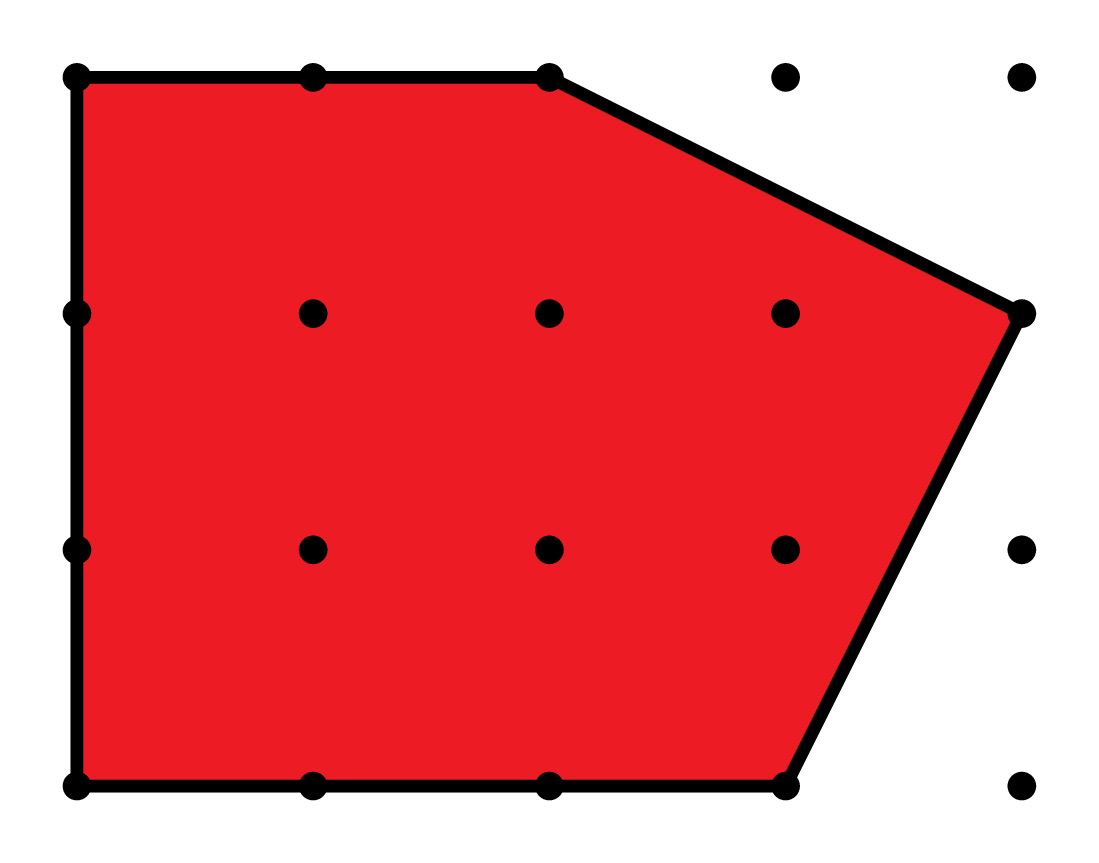
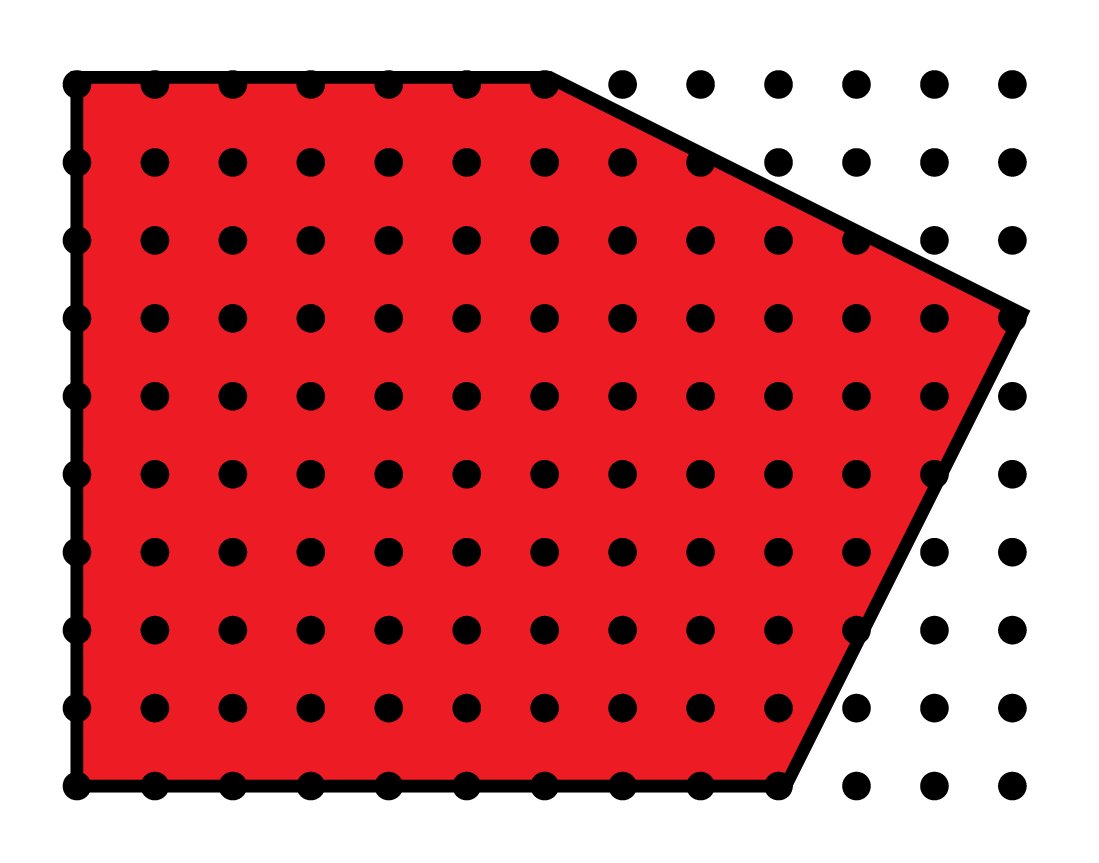
\(\mathbf{Z}^n\)
\(\frac{1}{2}\mathbf{Z}^n\)
\(\frac{1}{3}\mathbf{Z}^n\)
\#(kP \cap \mathbf{Z}^n) = \#(P \cap \tfrac{1}{k}\mathbf{Z}^n)
Consider how \(\mathscr{E}_{n,\ell}^{\Lambda}\) changes as we refine \(\mathbf{Z}^n\subseteq \Lambda\subset \mathbf{Q}^n\).
Represent a lattice \(\Lambda\) by a matrix, whose rows generate \(\Lambda\).
\mathbf{Z}^2 \leftrightsquigarrow \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
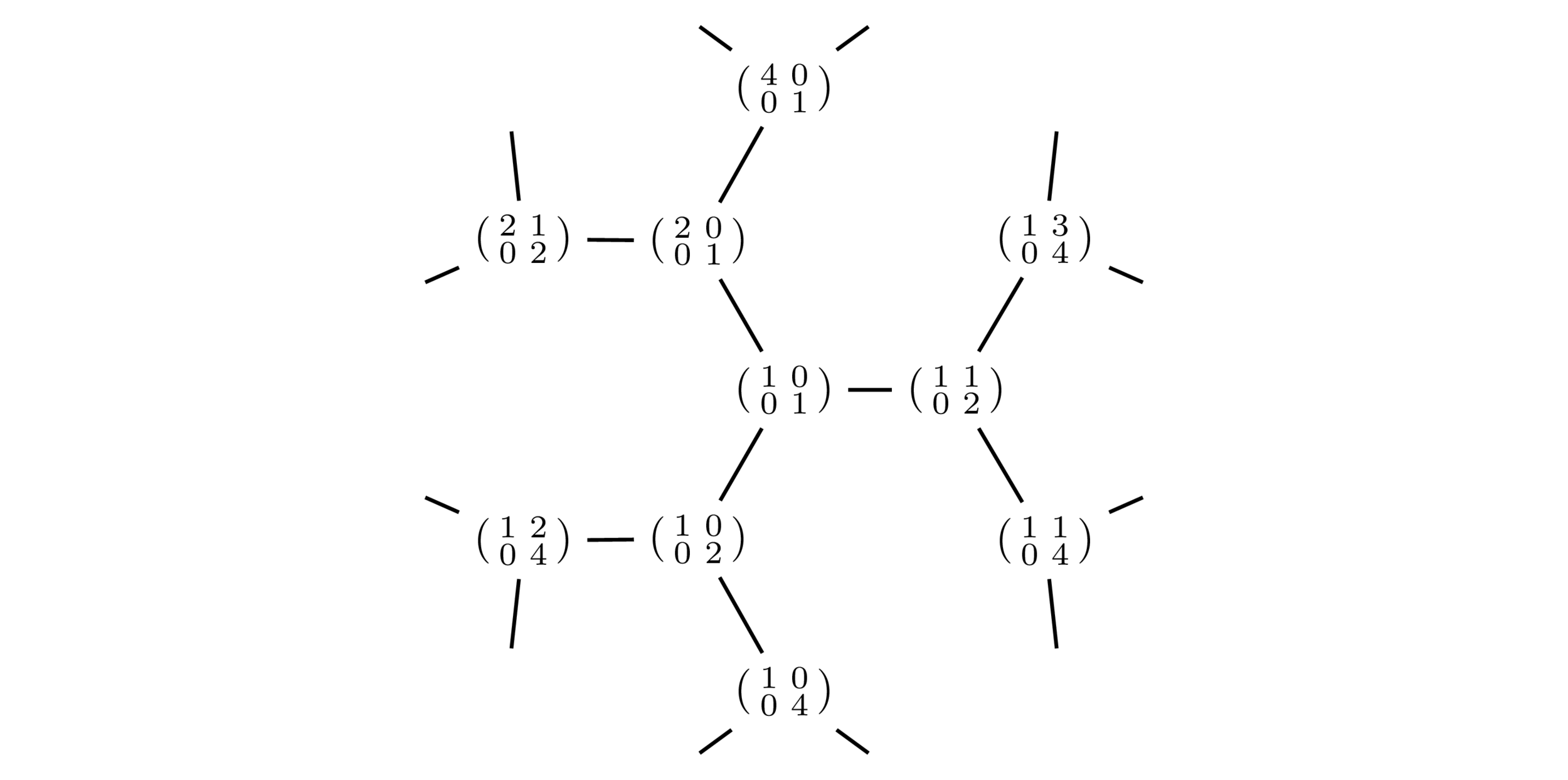
Lattices \(\Lambda\supseteq\mathbf{Z}^2\)
\Lambda = 2^{-1}\left(\begin{smallmatrix}
\phantom{0} & \phantom{0} \\ \phantom{0} & \phantom{0}
\end{smallmatrix}\right)
\Lambda = 4^{-1}\left(\begin{smallmatrix}
\phantom{0} & \phantom{0} \\ \phantom{0} & \phantom{0}
\end{smallmatrix}\right)
\Lambda \mapsto \mathcal{E}_{2, 1}^{\Lambda}(\phantom{poly})
\begin{aligned}
\mathrm{conv}&\{(0,0), (0,3), (2,3),\\
&\;(3,0), (4,2)\}
\end{aligned}
\begin{aligned}
\mathrm{conv}&\{(0,0), (0,2), (1,4),\\
&\;(3,2), (4,0)\}
\end{aligned}
\begin{aligned}
\mathrm{conv}&\{(0,0), (0,2), (1,4),\\
&\;(3,2), (4,0)\}
\end{aligned}
\begin{aligned}
\mathrm{conv}&\{(0,0), (0,1), (1,0)\}
\end{aligned}
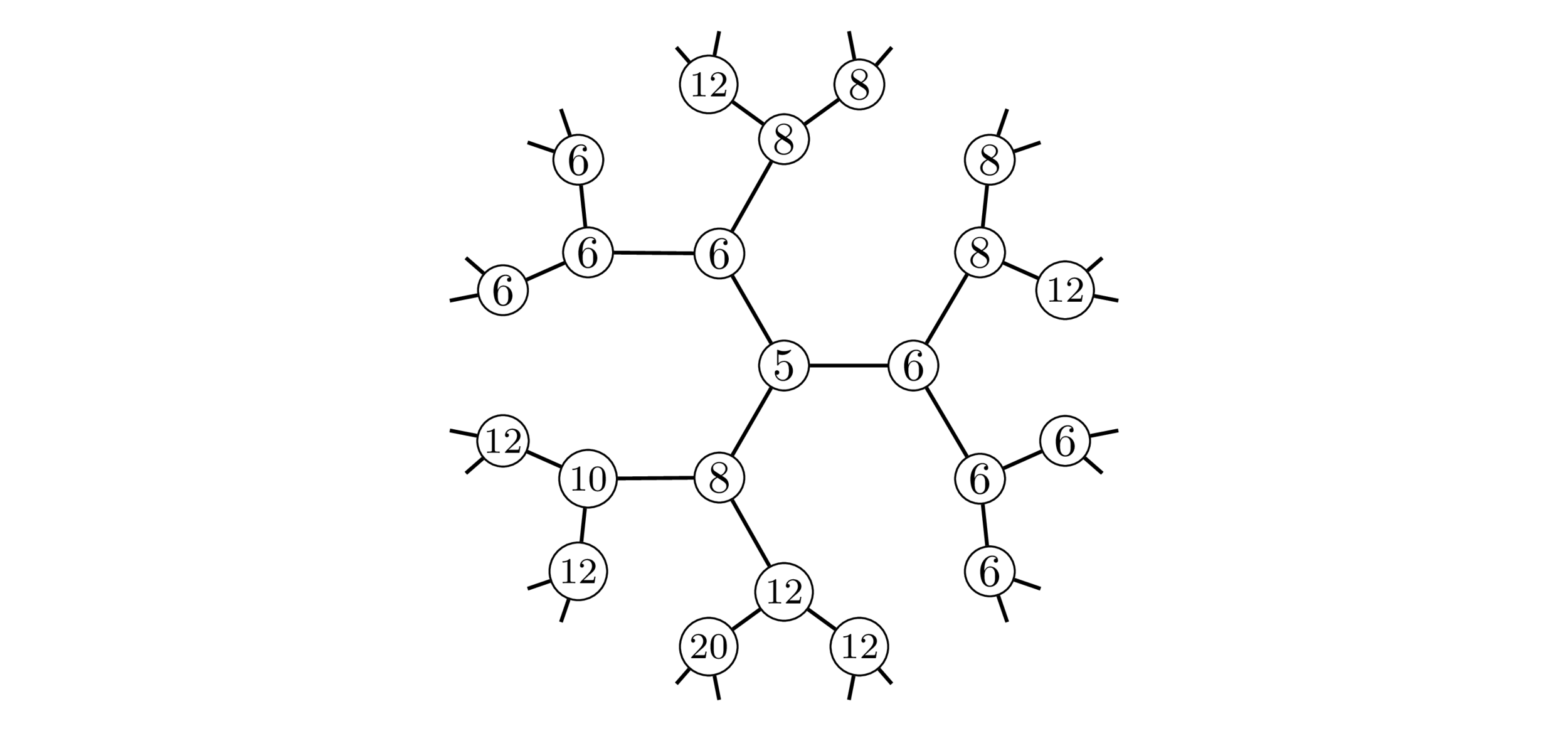
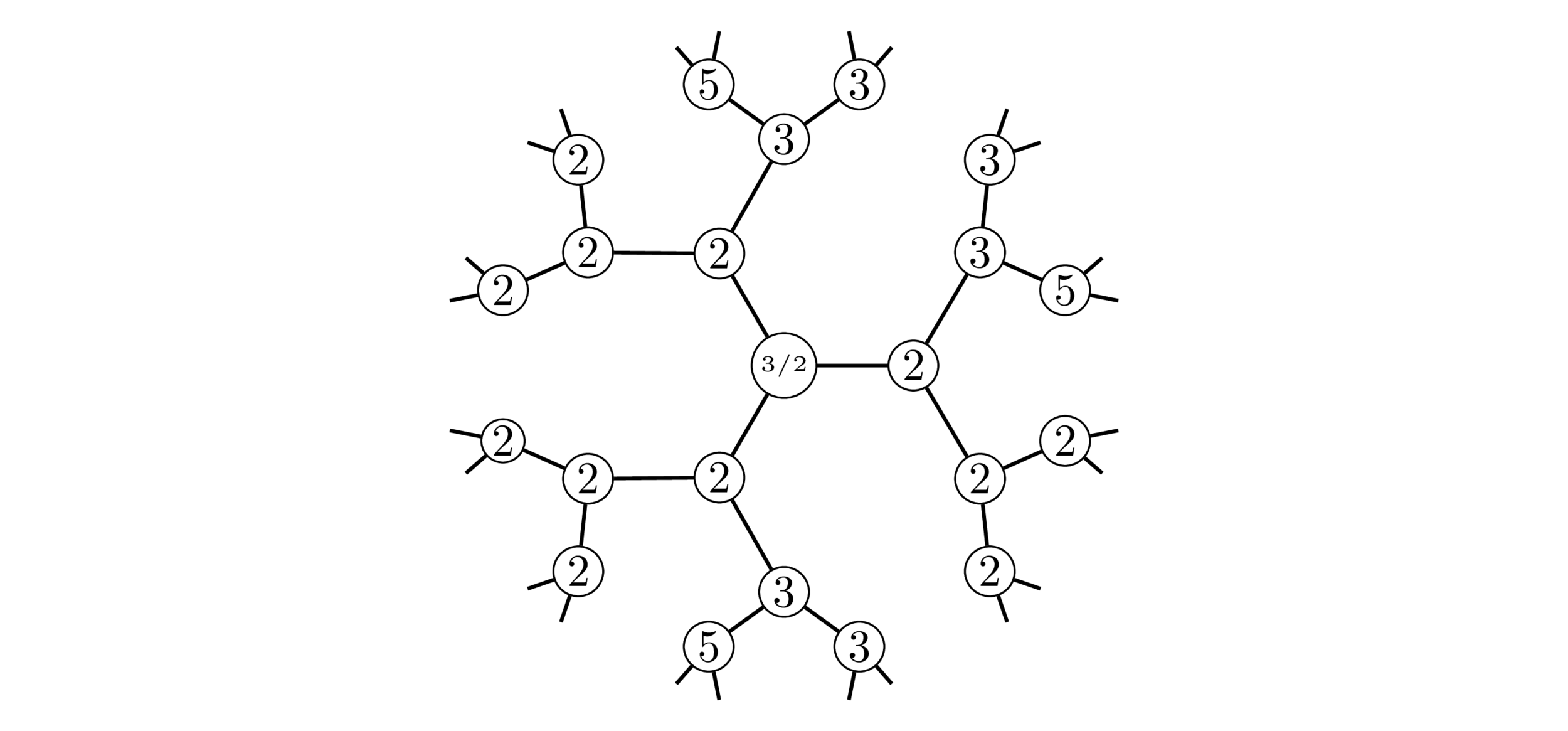
Normalized sums of coefficients
Fix a polytope \(P\), with \(\mathscr{E}_{n,\ell}(P)\neq 0\). Define
where \(\Lambda\supseteq\mathbf{Z}^n\) runs over all lattices in \(\mathbf{Q}^n\) with \(\#(\Lambda/\mathbf{Z}^n)=m\).
Just as a lattice generated from a matrix from \(\mathrm{GL}_n(\mathbf{Q})\cap\mathrm{Mat}_n(\mathbf{Z})\),
a symplectic lattice is generated from one in \(\mathrm{GSp}_{2n}(\mathbf{Q})\cap\mathrm{Mat}_{2n}(\mathbf{Z})\).
\mathcal{C}_{P,\ell}^{\mathsf{A}} : \mathbf{N} \longrightarrow \mathbf{Q}
m \longmapsto \dfrac{1}{\mathscr{E}_{n,\ell}(P)} \sum_{\Lambda} \mathscr{E}_{n,\ell}^{\Lambda}(P),
Define \(\mathcal{C}_{P,\ell}^{\mathsf{C}} : \mathbf{N}\to \mathbf{Q}\) similarly but restricted to symplectic lattices.
We computed \(\mathcal{C}_{P,1}^{\mathsf{A}}(2)\) and \(\mathcal{C}_{P,1}^{\mathsf{A}}(4)\).
An arithmetic function
Write \(\mathsf{X}\) for either \(\mathsf{A}\) or \(\mathsf{C}\).
Theorem (Alfes, M, & Voll (2025)).
(Independence) For polytopes \(P\) and \(Q\), with \(\dim P=\dim Q\),
(Multiplicativity) For \(a,b\in \mathbf{N}\) with \(\mathrm{gcd}(a,b)=1\),
\mathcal{C}_{P,\ell}^{\mathsf{X}}(ab) = \mathcal{C}_{P,\ell}^{\mathsf{X}}(a)\mathcal{C}_{P,\ell}^{\mathsf{X}}(b).
\mathcal{C}_{P,\ell}^{\mathsf{X}}=\mathcal{C}_{Q,\ell}^{\mathsf{X}}.
Growth rate of coefficients
For functions \(f,g : \mathbb{R}\to \mathbb{R}\), we write
f(N) \sim g(N) \quad \iff \quad \lim_{N\to \infty} \dfrac{f(N)}{g(N)} = 1.
Proposition (Alfes, M, & Voll (2025)).
Let \(\ell\in \{0,1,\dots, n\}\). Assuming \(\mathscr{E}_{n,\ell}(P)\neq 0\),
\sum_{m=1}^{N} \mathcal{C}_{P,\ell}^{\mathsf{A}}(m) \,\sim\, \begin{cases}
\frac{\zeta(n-\ell)}{n} \zeta(2)\zeta(3) \cdots \zeta(n-1) N^n & \text{if }\ell\leqslant n-2, \\[0.5em]
\frac{1}{n}\zeta(2)\zeta(3) \cdots \zeta(n-2) N^n \log N & \text{if }\ell=n-1, \\[0.5em]
\frac{1}{n+1} \zeta(2)\zeta(3) \cdots \zeta(n) N^{n+1} & \text{if }\ell=n.
\end{cases}
Here, \(\zeta\) is the Riemann zeta function.
Averaging over all lattices
Corollary.
Let \(P\) be an \(n\)-dimensional polytope in \(\mathbf{Z}^n\) and \(\ell\in \{0,1,\dots, n-2\}\). The average \(\ell\)th Ehrhart coefficient of \(P\), running over all \(\Lambda\supseteq\mathbf{Z}^n\) in \(\mathbf{Q}^n\) with finite co-index, approaches
\dfrac{\zeta(n-\ell)}{\zeta(n)} \mathscr{E}_{n,\ell}(P).
Example. For \(n=3\), the average linear coefficient approaches
\dfrac{\pi^2}{6\zeta(3)}\mathscr{E}_{3,1}(P) \approx 1.37\cdot\mathscr{E}_{3,1}(P)
Example. For \(n=4\), the average quadratic coefficient approaches
\dfrac{15}{\pi^2}\mathscr{E}_{4,2}(P) \approx 1.52\cdot \mathscr{E}_{4,2}(P)
Growth rate (symplectic edition)
Theorem (Alfes, M, & Voll (2025)).
For each \(\ell\in \{0,1,\dots, 2n\}\) there exists \(c_{n,\ell}\in\mathbb{R}\) such that
\sum_{m=1}^{N}\mathcal{C}_{P,\ell}^{\mathsf{C}}(m) \,\sim\, c_{n,\ell}\sqrt{N^{n+1}}\sqrt[n]{N^{\max(0,\ell-n)+1}}(\log N)^{\delta_{n,\ell}}
For \(i,j\in\mathbb{N}_0\), write \(\delta_{i,j}\) for the Kronecker delta symbol.
For \(n=2\) (i.e. in \(4\) dimensions) we completely know \(c_{2,\ell}\):
\begin{aligned}
c_{2,0} &= \frac{7\zeta(3)}{8}, &
c_{2,1} &= \frac{\zeta(2)^2\zeta(3)}{12\zeta(5)}, &
c_{2,2} &= \frac{5}{8}, &
c_{2,3} &= \frac{2\zeta(2)^2\zeta(3)}{5\zeta(5)}, &
c_{2,4} &= \frac{7\zeta(3)}{12}.
\end{aligned}
Averaging over symplectic lattices
When \(n=2\) and \(\ell=1\), the average linear coefficient is
Corollary.
Let \(P\) be \(2n\)-dimensional in \(\mathbf{Z}^{2n}\). The average \(\ell\)th Ehrhart coefficient, running over all symplectic lattices, converges only when \(\ell\in\{0,1,\dots, n-1\}\). Its limit is
\dfrac{c_{n,\ell}}{c_{n,0}} \mathscr{E}_{2n,\ell}(P).
\dfrac{\pi^4}{63\zeta(5)}\mathscr{E}_{4,1}(P) \approx 1.49 \cdot \mathscr{E}_{4,1}(P).
Modular form analogue
Previous theorems stem from the understanding extracted from the Hecke operators.
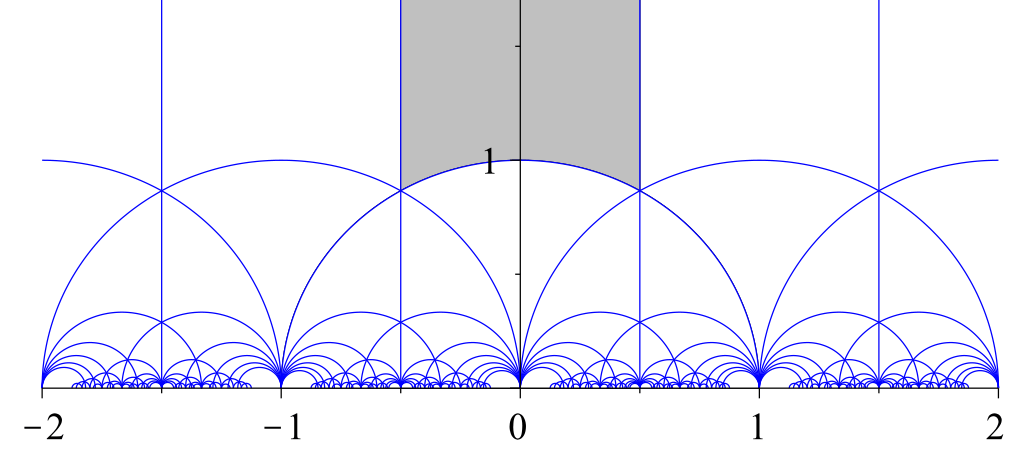
Points in \(\mathrm{SL}_2(\mathbf{Z})\setminus \mathbf{H}\)
\(\mathrm{GL}_n(\mathbf{Z})\setminus\{\text{Polytopes}\}\)
Modular form weight \(k\)
\(\mathscr{E}_{n,k}\)
\leftrightsquigarrow
\begin{aligned}
G^+ &= \mathrm{GSp}_{2n}(\mathbf{Q}_p)\cap \mathrm{Mat}_{2n}(\mathbf{Z}_p), &
\Gamma &= \mathrm{GSp}_{2n}(\mathbf{Z}_p)
\end{aligned}
The (symplectic) Hecke ring \(\mathcal{H}\) is the set of functions \(G^+ \to \mathbf{Z}\) that:
- are continuous (thus, locally constant),
- have compact support,
- are constant on \(\Gamma\)-double cosets.
\(\mathbf{Z}\)-basis for \(\mathcal{H}\) : characteristic functions on \(\Gamma\)-double cosets.
\mathcal{H} = \mathbf{Z}[T_0, T_1, \dots, T_n].
\begin{aligned}
D_0 &= \begin{pmatrix}
I_n & \\ & pI_n
\end{pmatrix}, &
D_k &= \begin{pmatrix}
I_{n-k} & & & \\
& pI_k & & \\
& & p^2I_{n-k} & \\
& & & pI_k
\end{pmatrix}.
\end{aligned}
We define matrices \(D_0,\dots, D_n\in G^+\): for \(k\in \{1,\dots, n\}\),
Let \(T_k\in\mathcal{H}\) be the characteristic function on \(\Gamma D_k\Gamma\). Thus,
(symplectic)
elemtary
divisors
For \(f\in\mathrm{UIV}_{2n}\), define \(Tf\in\mathrm{UIV}_{2n}\) via
where
\(\Gamma\setminus \Gamma g \Gamma\) : set of lattices with prescribed elementary divisors,
Extend linearly to define an action of \(\mathcal{H}\) on \(\mathrm{UIV}_{2n}\).
Let \(T\in\mathcal{H}\) be the characteristic function for \(\Gamma g\Gamma\), so associated with some elementary divisors.
What does this action look like on our generators \(T_k\)?
Tf(P) = \sum_{\Gamma h \,\in\, \Gamma \setminus \Gamma g\Gamma} f(h\cdot P)
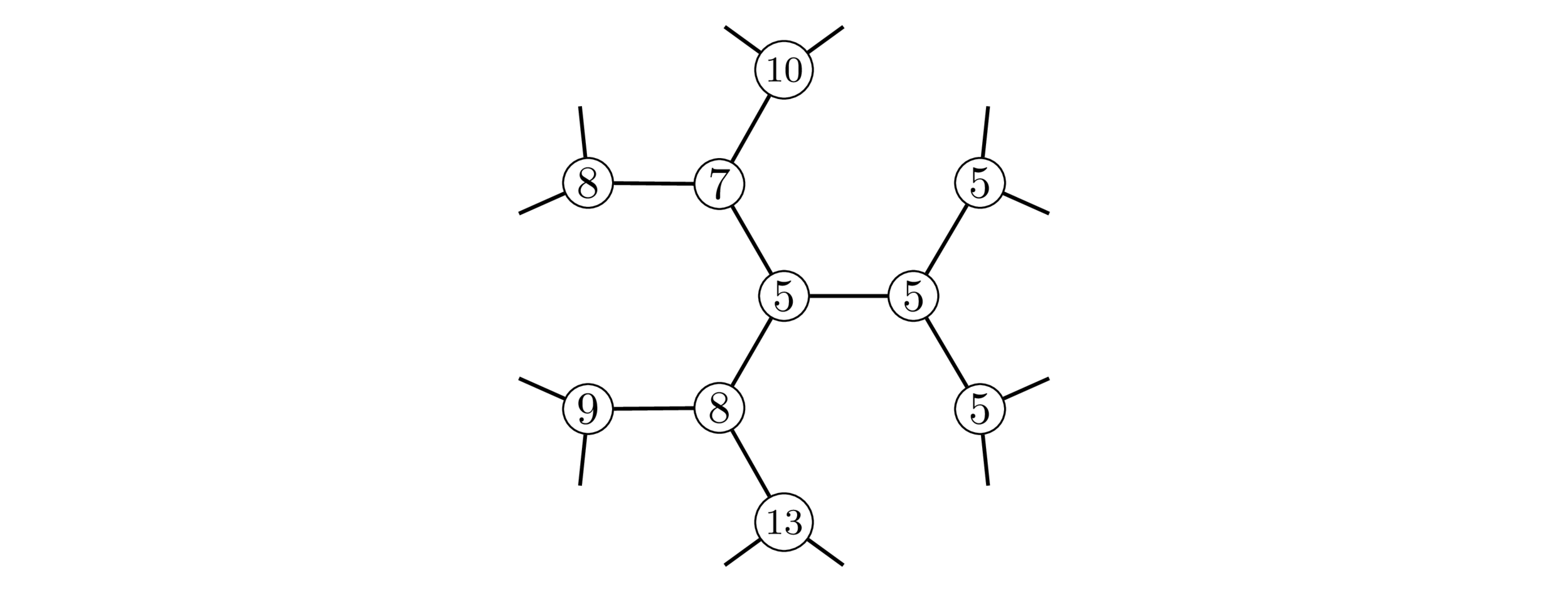
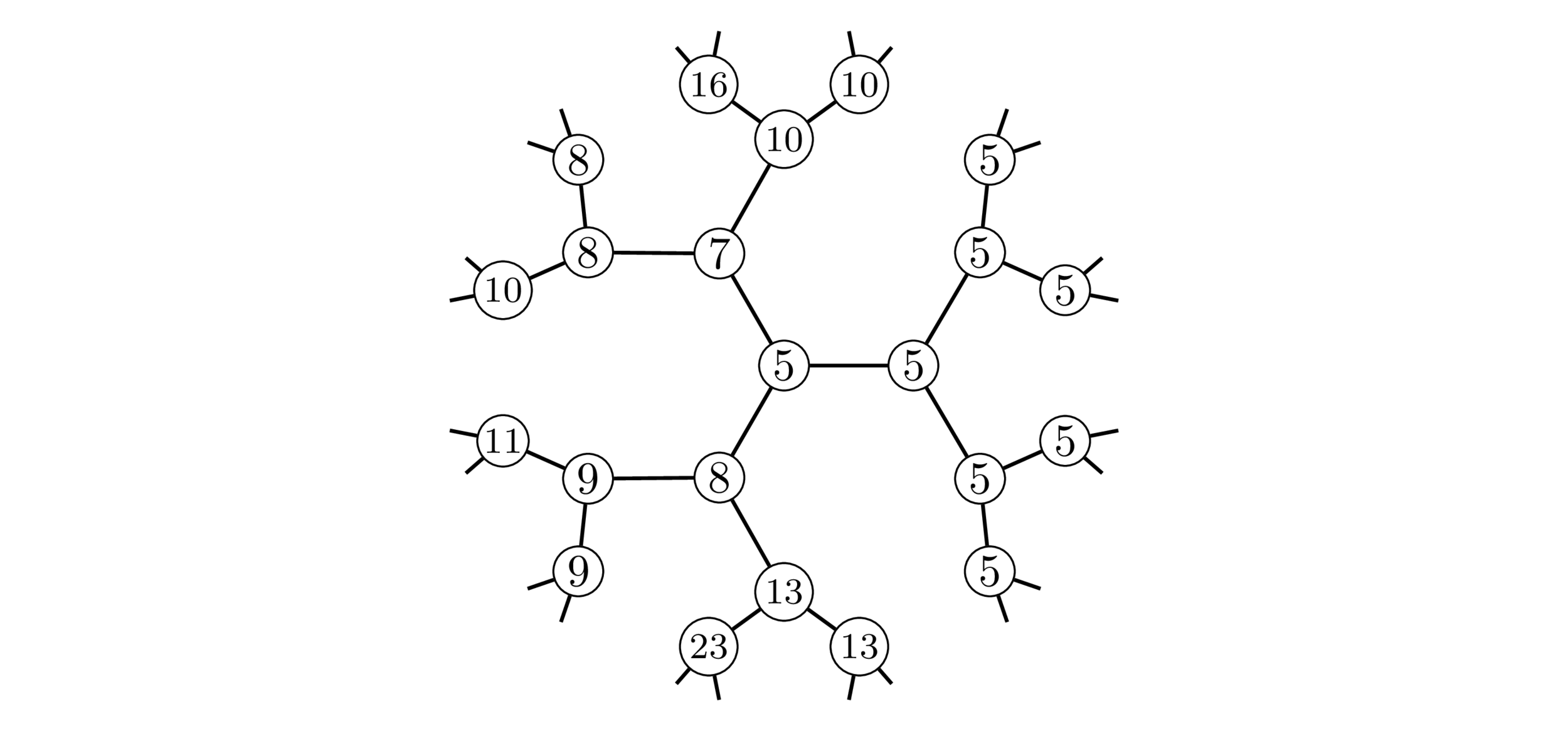
\(h\cdot P\) : given by some integer matrix in \(\Gamma h\) acting on vertices.
Each matrix corresponds to a \(\Gamma\)-left coset.
Colors correspond to \(\Gamma\)-double cosets.
\Gamma\begin{pmatrix}
1 \\ &1 \\ &&p \\ &&&p
\end{pmatrix}\Gamma
T_0
\Gamma\begin{pmatrix}
1 \\ &p \\ &&p^2 \\ &&&p
\end{pmatrix}\Gamma
T_1
\Gamma\begin{pmatrix}
p \\ &p \\ &&p \\ &&&p
\end{pmatrix}\Gamma
T_2
Knowing that the \(\mathscr{E}_{2n,\ell}\) form a symplectic Hecke eigenbasis means we can take advantage of the theory of spherical functions.
Leads to a nice interpretation of the associated zeta function:
\mathcal{Z}_{n,\ell,p}^{\mathsf{X}}(s) = \sum_{\Gamma g \,\in\, \Gamma\setminus \Gamma G^+\Gamma} \dfrac{\mathscr{E}_{2n,\ell}(g\cdot P)}{\mathscr{E}_{2n,\ell}(P)} \left|\Lambda_{g} : \Lambda_0\right|^{-s}.
Ehrhart–Hecke zeta functions
Lattice
from \(\Gamma g\)
To understand growth of \(\mathcal{C}_{P,\ell}^{\mathsf{X}}\), need to understand \(\mathcal{Z}_{n,\ell,p}^{\mathsf{X}}\) for all \(p\):
\mathcal{Z}_{n,\ell}^{\mathsf{X}}(s) := \sum_{m=1}^{\infty} \mathcal{C}_{P,\ell}^{\mathsf{X}}(m)\, m^{-s} = \prod_{p\text{ prime}} \mathcal{Z}_{n,\ell,p}^{\mathsf{X}}(s)
Main method of proof: lattice enumeration from M & Voll (2024).
\mathcal{Z}_{n,\ell}^{\mathsf{A}}(s) = \zeta(s - \ell) \cdot \zeta(s - 1) \zeta(s-2)\cdots \zeta(s - n + 1)
Type A case is simpler. We know the global zeta function:
\mathcal{Z}_{n,\ell,p}^{\mathsf{C}}(s) = \sum_{I,J\subseteq [n]} \Psi_{n,I,J}(p^{-1}) \prod_{i\in I}
\dfrac{p^{\binom{i+1}{2} + i(n-i)}t^n}{1-p^{\binom{i+1}{2} +
i(n-i)}t^n} \prod_{j\in J} \dfrac{p^{\binom{j+1}{2} + j(n-j) - n +
\ell}t^n}{1-p^{\binom{j+1}{2} + j(n-j) - n + \ell}t^n}
Theorem (Alfes, M, & Voll (2025)).
Setting \(t = p^{-s}\),
\Psi_{n,I,J}(Y) = \text{$Y$-multinomial coefficient} \times \prod (1 - Y^k)^{e_k}
Type C case is more subtle. We know the local zeta function:
Summary
The \(\mathscr{E}_{2n,\ell}\) form a symplectic Hecke eigenbasis of \(\mathrm{UIV}_{2n}\).
Theory of spherical functions on \(p\)-adic groups provide tools to study growth of coefficients.
Thank you!
- Unique* valuations with this property
- is \(\zeta(n-\ell)/\zeta(n)\) for \(\ell\in\{0,\dots, n-2\}\) over all lattices,
The average \(\ell\)th coefficient of the Ehrhart polynomial...
- converges for \(\ell\in \{0,\dots, \frac{2n}{2} - 1\}\) over sympletic lattices.
Average Ehrhart coefficients and symplectic Hecke eigenbases
By Josh Maglione
Average Ehrhart coefficients and symplectic Hecke eigenbases
Ehrhart showed that the function counting lattice points of dilates of lattice polytopes in Euclidean space is a polynomial. The coefficients of this polynomial, therefore, provide interesting information about the original lattice polytope. We consider the functions that map lattice polytopes to the l-th coefficient of their Ehrhart polynomials. These functions form a basis for the space of so-called unimodular invariant valuations. We show that, in even dimensions, these functions are in fact simultaneous symplectic Hecke eigenfunctions. We leverage this and apply the theory of spherical functions and their associated zeta functions to prove analytic, asymptotic, and combinatorial results about arithmetic functions averaging l-th Ehrhart coefficients. No prior knowledge of any of topics in this abstract should be necessary to enjoy this talk. We report on joint with Claudia Alfes and Christopher Voll.
