Dynamic Programming
simplify a complicated problem by breaking it down into simpler sub-problems in a recursive manner
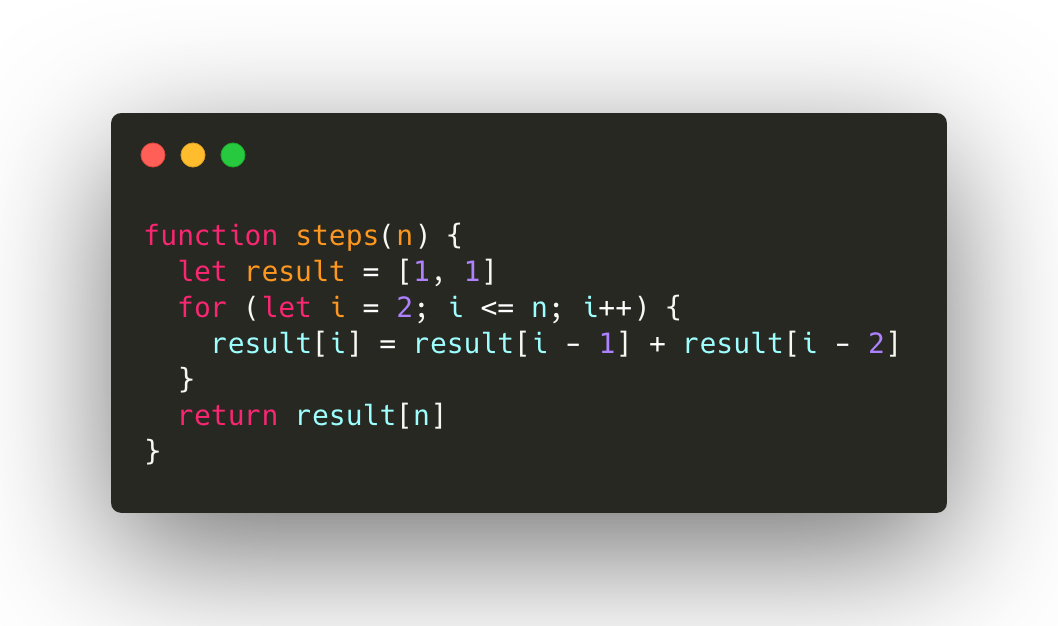
Q: Climbing Stairs
You are climbing a stair case.
It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps.
In how many distinct ways can you climb to the top?
EASY
Recursion
DP

Q: Perfect Squares
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.
NORMAL
Input: 12
Output: 3 (4+4+4)

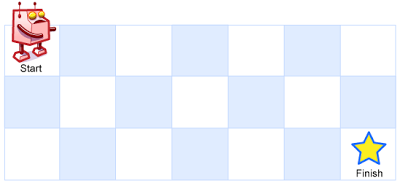
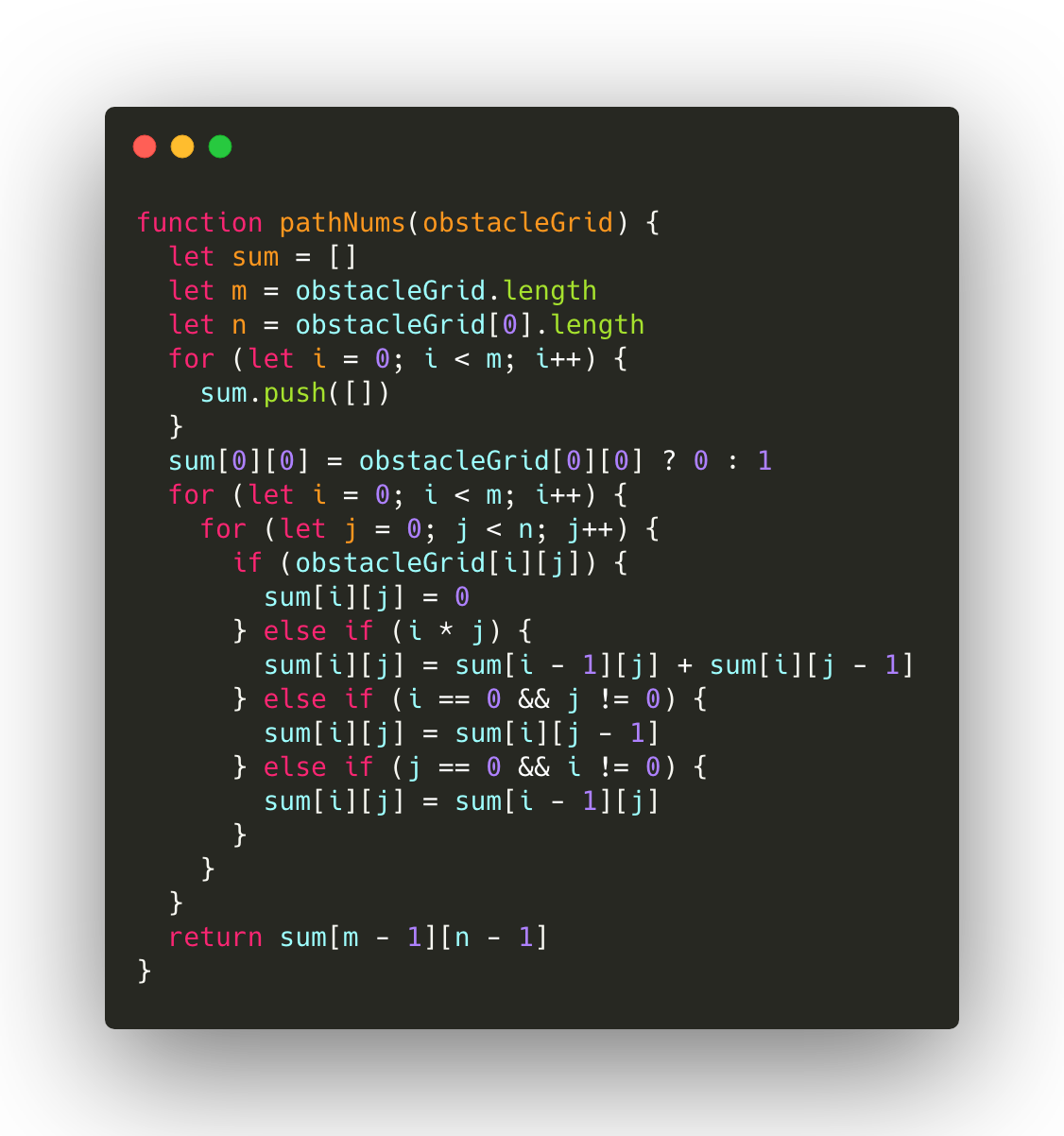
Q: Unique Paths
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?
NORMAL
Q: Unique Paths
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Q: Edit Distance
HARD
Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.
You have the following 3 operations permitted on a word:
1. Insert a character
2. Delete a character
3. Replace a character
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
1. define the state dp[i][j] to be the minimum number of operations to convert word1[0..i) to word2[0..j)
2. For the base case, dp[i][0] = i and dp[0][j] = j
3. if word1[i - 1] == word2[j - 1], then no more operation is needed and dp[i][j] = dp[i - 1][j - 1]
4. If word1[i - 1] != word2[j - 1], we need to consider three cases.
Replace word1[i - 1] by word2[j - 1] (dp[i][j] = dp[i - 1][j - 1] + 1);
If word1[0..i - 1) = word2[0..j) then delete word1[i - 1] (dp[i][j] = dp[i - 1][j] + 1);
If word1[0..i) + word2[j - 1] = word2[0..j) then insert word2[j - 1] to word1[0..i) (dp[i][j] = dp[i][j - 1] + 1).
So dp[i][j] will just be the minimum of the above three cases.

Thank you
Dynamic Programming
By Joson Chen
Dynamic Programming
- 269



