A generalized semi-supervised elastic-net
Juan C. Laria
juancarlos.laria@uc3m.es
The semi-supervised framework
unsupervised
The semi-supervised framework
supervised
The semi-supervised framework
semi-supervised
The semi-supervised framework
semi-supervised
transfer-model
Elastic-net regularization
\|\bm{y} - \bm{X}\bm{\beta} \|_2^2 + \lambda_1 \|\bm{\beta}\|_1+
\lambda_2 \|\bm{\beta}\|_2^2
lasso
ridge
\bm{X}, \bm{y}
Joint trained elastic-net
\|\bm{y} - \bm{X}\bm{\beta} \|_2^2 + \gamma_1\|T(\gamma_2)\bm{\beta}\|_2^2 + \lambda_1 \|\bm{\beta}\|_1+ \lambda_2 \|\bm{\beta}\|_2^2
T(\gamma_2) = \sqrt{\gamma_2}\bm{U}(\bm{\Sigma}^2 + \gamma_2\bm{I})^{-1/2} \bm{U}^\top \bm{X}_U
\bm{X}_U = \bm{U \Sigma V}^\top
\bm{X}, \bm{y} , \bm{X}_U
Culp, M. (2013). On the semisupervised joint trained elastic net. Journal of Computational and Graphical Statistics 22 (2), 300–318.
Extended linear joint trained framework
\|\bm{y} - \bm{X}\bm{\beta} \|_2^2 + \gamma_1\|T(\gamma_2, \gamma_3)\bm{\beta}\|_2^2
T(\gamma_2, \gamma_3) = \sqrt{\gamma_2}\bm{U}(\bm{\Sigma}^2 + \gamma_2\bm{I})^{-1/2} \bm{\Sigma} \bm{V}^\top + \gamma_3 \bm{1} \bm{\mu}^\top.
\bm{X}_U - \bm{1}\bm{\mu}^\top = \bm{U \Sigma V}^\top
\bm{X}, \bm{y} , \bm{X}_U
Søgaard Larsen, J. et. al (2020). Semi-supervised covariate shift modelling of spectroscopic data. (in-press)
Semi-supervised elastic-net
L(\bm{\beta}~|~\bm{y},\bm{X}) + \gamma_1 L(\bm{\beta}~|~\bar{\bm{y}} , T(\gamma_2, \gamma_3))+ \lambda_1\|\bm{\beta}\|_1 + \lambda_2\|\bm{\beta}\|_2^2
T(\gamma_2, \gamma_3) = \sqrt{\gamma_2}\bm{U}(\bm{\Sigma}^2 + \gamma_2\bm{I})^{-1/2} \bm{\Sigma} \bm{V}^\top + \gamma_3 \bm{1} \bm{\mu}^\top.
\bm{X}_U - \bm{1}\bm{\mu}^\top = \bm{U \Sigma V}^\top
\bm{X}, \bm{y} , \bm{X}_U
\| \cdot \|_2^2
logit()
\bm{X}_U = \bm{U \Sigma V}^\top
T(\gamma_2) = \sqrt{\gamma_2}\bm{U}(\bm{\Sigma}^2 + \gamma_2\bm{I})^{-1/2} \bm{U}^\top \bm{X}_U
T(\gamma_2, \gamma_3)
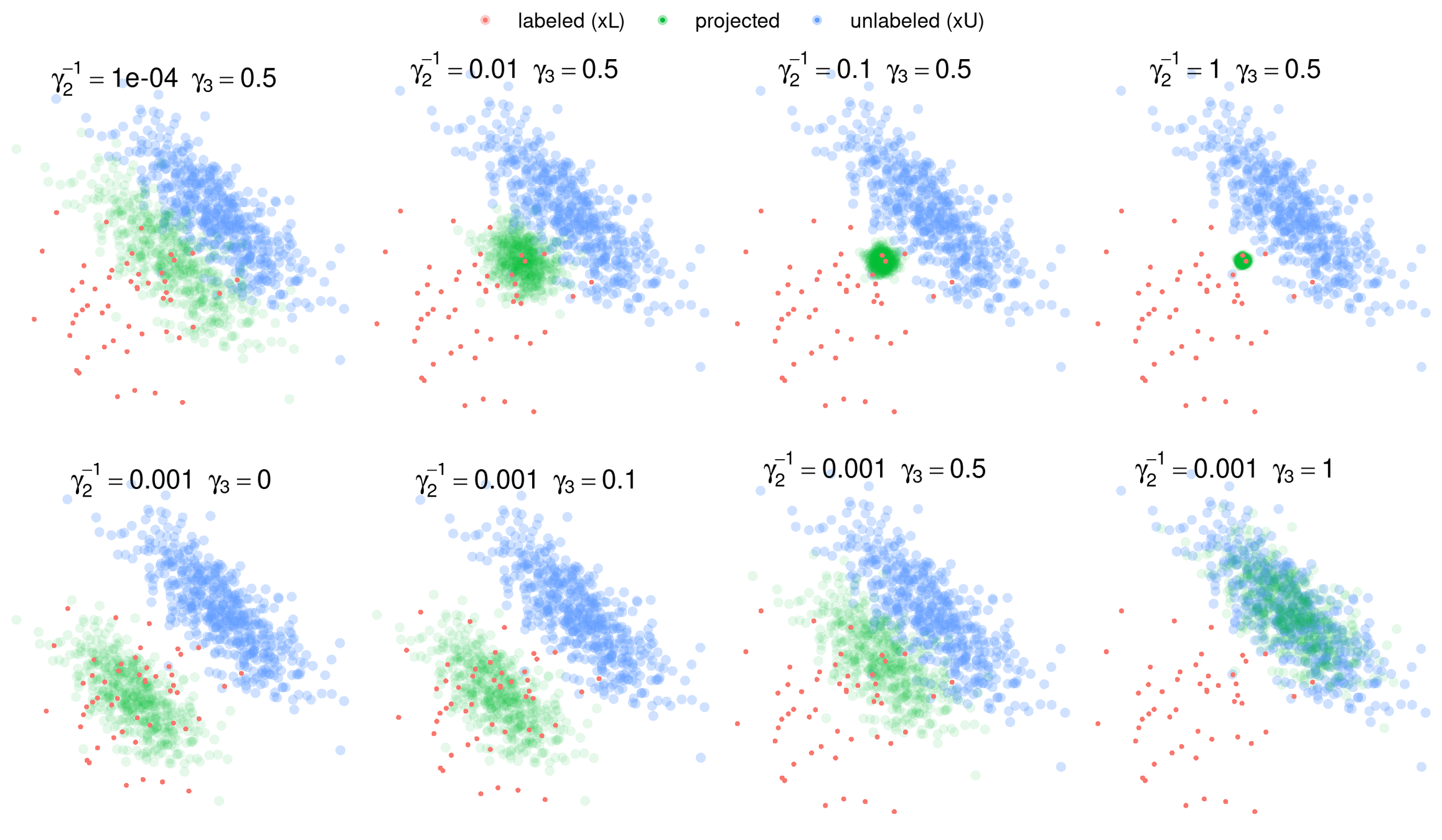
Optimization
L(\bm{\beta}) + \lambda_1\|\bm{\beta}\|_{1} + \lambda_2\|\bm{\beta}\|_{2}^2\\
\textnormal{ where }\\
L(\bm{\beta}) = R(\bm{\beta}~|~\bm{y},\bm{X}) + \gamma_1 R(\bm{\beta}~|~\bar{\bm{y}} , T(\gamma_2, \gamma_3))
elastic-net with custom loss function
- Fast iterative shrinkage-thresholding algorithm (FISTA)
- Acelerated (block) gradient descent approach
Implementation
-
We develop a flexible and fast implementation for s2net in R, written in C++ using RcppArmadillo and integrated into R via Rcpp modules.
-
The software is available in the s2net package
install.packages("s2net")
library(s2net)
vignette(package = "s2net")Hyper-parameter tuning
library(cloudml)
cloudml_train("main_script.R", config = "tuning.yml")FLAGS <- flags(
flag_numeric("lambda1", 0.01, "Lasso weight"),
flag_numeric("lambda2", 0.01, "Ridge weight"),
flag_numeric("gamma1", 0.1, "s2net global weight"),
flag_numeric("gamma2", 100, "s2net covariance parameter"),
flag_numeric("gamma3", 0.5, "s2net shift parameter")
)- Cloud based solution
- Easy to implement
- Blackbox grid/random search, bayesian optimization available
- Limited resources in the free tier
- Can be pricey
- Slow - not suitable for fast algorithms
- All dependencies should be available from CRAN - otherwise it is very difficult to make it work
Hyper-parameter tuning
- Cloud based solution that runs locally
- Extremely fast, given the hardware
- Open source
- Very difficult to implement
- Needs local hardware, or renting a cluster in the cloud
- Native scala hyper-parameter tuning functions are only available for popular methods.
- You have to implement your search function that works with your method.
library(sparklyr)
result = spark_apply(grid, my_function, context = datos)THANK you!
s2net
By Juan Carlos Laria