Rigid Motions on Discrete Spaces
by Kacper Pluta
Show me a Rigid Motion
Solar System Animation: https://youtu.be/gvSUPFZp7Yo
\left|
\begin{array}{lllll}
\mathcal{U} & : & \mathbb{C} & \to & \mathbb{C} \\
& & \mathbf{x} & \mapsto & \mathbf{a} \cdot \mathbf{x} + \mathbf{t}
\end{array}
\right.
Rigid Motions on
\mathbb{C}
Properties
- Do preserve distances
- Bijective
\mathbf{a}
- a unit modulus complex number
\mathbf{t}
- a complex number
\theta = \arg(\mathbf{a})
- a rotation angle
\left|
\begin{array}{lllll}
\mathcal{U} & : & \mathbb{R}^2 & \to & \mathbb{R}^2 \\
& & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t}
\end{array}
\right.
Rigid Motions on
\mathbb{R}^2
\mathbf{R}
- a rotation matrix
\mathbf{t}
- a translation vector
Properties
-
Isometry
-
Bijective
Show me a Discrete Object
Show me a Digitized Rigid Motion
U = \mathcal{D}\ \circ \mathcal{U}
Properties
- Non-injective
- Non-surjective
- Do not preserve distances
\mathcal{U}
Digitized Rigid Motions
where
\mathcal{D}
is a digitization operator
U = \mathcal{D}\ \circ \mathcal{U}
Properties
- Non-injective
- Non-surjective
- Do not preserve distances
\mathcal{U}
Digitized Rigid Motions
where
\mathcal{D}
is a digitization operator
Agenda
Part I: 2D Discrete Spaces
- Introduction to 2D Regular Grids
- Neighborhood Motion Maps
- Digitized Rigid Motions on Square vs. Hexagonal Grids
- Bijective Digitized Rotations on Square Grid
Part II: 3D Digital Space
- Introduction to Cubic Grid
- Quick Introduction to 3D Rigid Motions
- Spatial Rotations and Quaternions
- Bijectivity of 3D Digitized Rotations
Conclusion & Perspectives
Part I:
2D Discrete Spaces
Contributions in Short
- A general framework to study digitized rigid motions
- Comparison of the digitized rigid motions defined on the square and hexagonal grids
-
Characterization of bijective digitized:
- rigid motions on the square grid
- rotations on the hexagonal grid
- Three algorithms to characterize if a digitized rigid motion is bijective when restricted to a finite set
I Am Going to Talk About
- A general framework to study digitized rigid motions
- Comparison of the digitized rigid motions defined on the square and hexagonal lattices
- Characterization of bijective digitized rigid motions on the square grid
Introduction to 2D Regular Grids
The Lattices
\mathbb{Z}[\omega] = \mathbb{Z} \oplus \mathbb{Z}\omega, \omega = -\frac{1}{2} + \frac{\sqrt{3}}{2} i
The grids are then denoted by
\mathcal{H}
\mathbb{Z}[i] = \mathbb{Z} \oplus \mathbb{Z}i
Eisenstein:
and Gaussian:
integers
Properties
| Property | Gaussian integers | Eisenstein integers |
|---|---|---|
| conjugate | ||
| squared modulus | ||
| units |
\bar{\mathbf{x}} = a - b i
\bar{\mathbf{x}} = (a - b) - b \omega
| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 + b^2
| \mathbf{x} | = \mathbf{x} \cdot \bar{\mathbf{x}} = a^2 - a b + b^2
\Upsilon = \{ \pm 1, \pm i \}
\Upsilon = \{ \pm 1, \pm \omega, \pm \bar{\omega} \}
| divisibility |
\mathbf{y} | \mathbf{x} \text{ if } \exists \mathbf{z} \in \mathbb{Z}[\varkappa] \text{ such that } \mathbf{x} = \mathbf{y}
\cdot \mathbf{z} \text{ and } \mathbf{y} \in \mathbb{Z}[\varkappa]
| greatest common divisor |
|
\gcd(\mathbf{x}, \mathbf{y}) = \mathbf{z} \in \mathbb{Z}[\varkappa]\text{ is defined as a largest }
\mathbf{z} \in \mathbb{Z}[\varkappa]\text{ (up to multiplications by units) which }
\text{divides both } \mathbf{x}\text{ and }\mathbf{y}
\text{Giving } a, b \in \mathbb{Z}\text{ and }\mathbf{x},\mathbf{y}, \in \mathbb{Z}[\varkappa], \varkappa \in \{i, \omega\}
Square grid
+ Memory addressing
+ Sampling is easy to define
Hexagonal grid
+ Uniform connectivity
+ Equidistant neighbors
+ Sampling is optimal
- Sampling is not optimal (ask bees)
- Neighbors are not equidistant
- Connectivity paradox
- Memory addressing is not trivial
- Sampling is difficult to define
Pros and Cons
Square grid
+ Memory addressing
+ Sampling is easy to define
Hexagonal grid
+ Uniform connectivity
+ Equidistant neighbors
+ Sampling is optimal
~ Memory addressing is not trivial
~ Sampling is difficult to define
Pros and Cons
- Sampling is not optimal (ask bees)
- Neighbors are not equidistant
~ Connectivity paradox
Digitization Model
A digitization cell of
0
denoted by
\mathcal{C}(0).
Digitization Model
The digitization operator is defined as
\mathcal{D}: \mathbb{C} \rightarrow \mathbb{Z}[\varkappa]
such that
\forall \mathbf{x} \in \mathbb{C}, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}[\varkappa]
\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).
and
\mathbf{p}
\mathbf{k}
From Continuous to Discrete
Neighborhood Motion Maps
Bijective Digitized Rotations on Hexagonal Lattice
Conditions for Bijectivity
Conditions for Bijectivity
A digitized rotation is bijective if and only if
\forall \mathbf{p} \in \mathbb{Z}[\omega] \; \exists ! \mathbf{q} \in \mathbb{Z}[\omega]
such that
\mathcal{U}(\mathbf{q}) \in \mathcal{C}(\mathbf{p}).
\mathcal{U}
- a continuous rotation
\mathcal{C}(\mathbf{p})
- a digitization cell centered at
\mathbf{p}
\mathbb{Z}[\omega]
- the hexagonal lattice
Conditions for Bijectivity
"Double" Surjectivity Condition for Bijectivity
\mathbf{a} \in \mathbb{C}
\mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(\mathcal{U}(\mathbf{q}))
- a complex number
- a rotated digitization cell
Set of Remainders
The "double" surjectivity condition is then
provided that
S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_1(0) =
S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\frac{\mathbf{a}}{|\mathbf{a}|}}(0).
Set of Remainders
The "double" surjectivity condition is then
provided that
S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{\mathbf{a}}(0) =
S_{\mathbf{a}}(\mathbb{Z}[\omega], \mathbb{Z}[\omega]) \cap \mathcal{C}_{|\mathbf{a}|}(0).
Factorization of Primitive Eisenstein Integers
s, t \in \mathbb{Z}
0 < s < t
and
t - s
not being divisible by 3.
a = s^2 + 2 s t, b = t^2 + 2 s t
and
c = s^2 + t^2 + s t,
such that
Factorization of Primitive Eisenstein Integers
A bunch of facts
Set of Remainders
The "double" surjectivity condition is then
provided that
Proving Bijectivity
Proving Bijectivity
Step 1: For which s and t,
or
are in the green but not in
the black hexagonal cell.
Proving Bijectivity
Proving Bijectivity
From the equation of the green line we obtain:
Proving Bijectivity
From the equation of the green line we obtain:
Then, we substitute t with s + e to arrive at
which are violated when s = 1 or when s > 1 and e = 1.
Proving Bijectivity
There are few more things to check in this step. See the manuscript (Lemma 5.3)/article (Lemma 7).
Proving Bijectivity
Step 2: Check if for s = 1 or s > 1 and e = 1, the uncommon space of the hexagonal cells does not contain Eisenstein integers.
s = 1
s > 1, t = s + 1
Proving Bijectivity
The Square Grid
The Hexagonal Grid
Neighborhood
The neighborhood of
\mathbf{p} \in \mathbb{Z}[\varkappa]
(of squared radius
r \in \mathbb{R}_+
):
\mathcal{N}_r(\mathbf{p}) = \big\{ \mathbf{p} + \mathbf{d} \in \mathbb{Z}[\varkappa] \mid |\mathbf{d} |^2 \leq r \big\}
Neighborhood Motion Maps
r \in \mathbb{R}_+
U
and
\left|
\begin{array}{lllll}
\mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\
& & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}).
\end{array}
\right.
\mathbf{p}
\mathbf{p}
The neighborhood motion map of
\mathbf{p} \in \mathbb{Z}[\varkappa]
for a given rigid motion
Neighborhood Motion Maps
r \in \mathbb{R}_+
U
and
\left|
\begin{array}{lllll}
\mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\
& & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}).
\end{array}
\right.
\mathbf{p}
\mathbf{p}
The neighborhood motion map of
\mathbf{p} \in \mathbb{Z}[\varkappa]
for a given rigid motion
Neighborhood Motion Maps
The neighborhood motion map of
\mathbf{p} \in \mathbb{Z}[\varkappa]
for a given rigid motion
r \in \mathbb{R}_+
U
and
\left|
\begin{array}{lllll}
\mathcal{G}^U_r & : & \mathcal{N}_r(0) & \to & \mathcal{N}_{r'}(0) \\
& & \mathbf{d} & \mapsto & U(\mathbf{p} + \mathbf{d}) - U(\mathbf{p}).
\end{array}
\right.
\mathbf{p}
\mathbf{p}
Remainder Map Step-by-Step
\mathbf{p}
Remainder Map step-by-step
\mathbf{p}
Remainder Map Step-by-Step
\mathcal{U}(\mathbf{p} + \mathbf{d}) =
\mathbf{a} \cdot \mathbf{d}
+\ \mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p} + \mathbf{d})
Remainder Map Step-by-Step
\mathcal{U}(\mathbf{p} + \mathbf{d}) =
\mathbf{a} \cdot \mathbf{d}
+\ \mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p} + \mathbf{d})
U(\mathbf{p})
\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
Remainder Map Step-by-Step
Without loss of generality,
U(\mathbf{p})
is the origin, and then
\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
\mathbf{a} \cdot \mathbf{d}
\mathbf{d}
\mathcal{U}(\mathbf{p}) - U(\mathbf{p})
Remainder Map Step-by-Step
Without loss of generality,
U(\mathbf{p})
is the origin, and then
\mathcal{U}(\mathbf{d}) = \mathbf{a} \cdot \mathbf{d} + \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
\mathbf{a} \cdot \mathbf{d}
\mathbf{d}
\mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(\mathbf{p})
\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
Remainder Map Step-by-Step
The remainder map defined as
\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})
where the range
\mathcal{C}(\mathbf{0})
is called the remainder range.
\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
Remainder Map Step-by-Step
The remainder map defined as
\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p}) \in \mathcal{C}(\mathbf{0})
where the range
\mathcal{C}(\mathbf{0})
is called the remainder range.
\mathcal{F}(\mathbf{p}) = \mathcal{U}(\mathbf{p}) - U(\mathbf{p})
U(\mathbf{p})
\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
Remainder Map and Critical Rigid Motions
Remainder Map and Critical Rigid Motions
U(\mathbf{p})
\mathcal{U}(\mathbf{p})
\mathcal{U}(\mathbf{p}+\mathbf{d})
Such critical cases can be observed via the relative positions of ,
\mathcal{F}(\mathbf{p})
\mathcal{H} - \mathbf{a} \cdot \mathbf{d}
That is to say
\mathcal{C}(\mathbf{0}) \cap (\mathcal{H} - \mathbf{a} \cdot \mathbf{d}).
and are formulated as the translations .
Remainder Map and Critical Rigid Motions
\mathcal{H} - \mathbf{a} \cdot \mathbf{d}
Critical Lines
\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
Critical Lines
\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
Critical Line Segments
\mathscr{H} = \bigcup \limits_{\mathbf{d} \in \mathcal{N}_r(0)} (\mathcal{H} - \mathbf{a}\cdot \mathbf{d}) \cap \mathcal{C}(0)
Frames
Each region bounded by the critical line segments is called a frame.
Frames
Each region bounded by the critical line segments is called a frame.
Frames
Each region bounded by the critical line segments is called a frame.
Frames
For any
\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})
if and only if
\mathcal{F}(\mathbf{p})
and
\mathcal{F}(\mathbf{q})
the same frame.
Proposition
are in
Frames
For any
\mathbf{p}, \mathbf{q} \in \mathbb{Z}[\varkappa], \mathcal{G}^U_r(\mathbf{p}) = \mathcal{G}^U_r(\mathbf{q})
if and only if
\mathcal{F}(\mathbf{p})
and
\mathcal{F}(\mathbf{q})
the same frame.
Proposition
are in
Remainder Range Partitioning
At most 25 frames per partitioning.
Remainder Range Partitioning
At most 81 frames per partitioning.
Remainder Range Partitioning
At most 49 frames per partitioning.
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Neighborhood Motion Maps Graph
Preservation of Information
Non-injective and Non-surjective Digitized Rigid Motions
Non-injective and Non-surjective Digitized Rigid Motions
Non-injective and Non-surjective Digitized Rigid Motions
Loss of Information
\mathcal{F}(\mathbb{Z}[i])
Pythagorean Rotations
If
\cos\theta
and
\sin\theta
are rational numbers, then the remainder map has
a finite number of images.
\mathcal{F}(\mathbb{Z}[i])
Pythagorean Rotations
There exists a one-to-one relation between primitive Pythagorean
Lemma
triples:
(a,b,c) \in \mathbb{Z}^3, a < b < c \text{ and } \gcd(a,b,c) = 1
and rational
rotations.
\mathcal{F}(\mathbb{Z}[i])
Pythagorean Rotations
Such primitive Pythagorean triples can be generated from:
p, q \in \mathbb{Z}
such that
0 < q < p
and
p - q
being odd.
Finally,
a = p^2 - q^2, b = 2 p q
and
c = p^2 + q^2.
\mathcal{F}(\mathbb{Z}[i])
Pythagorean Rotations
The number of images of the remainder map is equal to
Corollary
c\text{.}
\mathcal{F}(\mathbb{Z}[\omega])
For what kinds of parameters has the remainder map a finite number of images?
Eisenstein Rational Rotations
Eisenstein Rational Rotations
If
\cos\theta = \frac{2a -b}{2 c}
and
\sin\theta = \frac{\sqrt{3}b}{2 c}
where
(a,b,c)\in \mathbb{Z}^3, \gcd(a,b,c) = 1
and
0 < a < c < b,
Proposition
then the remainder map has a finite number
of images equal to
\mathcal{F}(\mathbb{Z}[\omega])
c\text{.}
Eisenstein Rational Rotations
\mathcal{F}(\mathbb{Z}[\omega])
is a primitive Eisenstein triple which can be
s, t \in \mathbb{Z}
such that
0 < s < t
and
t - s
not being
divisible by 3. Finally,
a = s^2 + 2 s t, b = t^2 + 2 s t
and
c = s^2 + t^2 + s t.
(a,b,c) \in \mathbb{Z}^3
Such
generated from:
Loss of Information
Bijective Digitized Rigid Motions on Square Grid
Which Digitized Rigid Motions are Bijective?
Question 1: Can non-rational rigid motions be bijective?
Question 1: Can non-rational rigid motions be bijective?
Question 2: Can a non-bijective rational rotation followed by a translation be bijective?
Globally Bijective Digitized Rigid Motions
Globally Bijective Digitized Rigid Motions
Question 3: What are the possible translations which can be applied with a bijective digitized rotation?
f_\downarrow^0
c
s
r
w
What are the possible translations which can follow a bijective digitized rotation?
What are the possible translations which can follow a bijective digitized rotation?
\phi
\psi
What are the possible translations which can follow a bijective digitized rotation?
c
s
r
w
A digitized rigid motion is bijective if and only if it is composed of a rotation by an angle defined by a twin Pythagorean triple (a, b, c) and a translation
\mathbf{t} = \mathbf{t}' + \mathbb{Z}\psi + \mathbb{Z}\phi,
\phi
\psi
where
\mathbf{t}' \in \left(-\frac{1}{2c}, \frac{1}{2c}\right) \oplus \left(-\frac{1}{2c}, \frac{1}{2c} \right) i.
Proposition
Bijective Digitized Rigid Motions of Finite Subsets of The Square Grid
\mathbb{Z}[i]
Is a given digitized rigid motion bijective when restricted to a finite subset of
?
Bijective Digitized Rigid Motions Are Not Dense
\mathcal{F}(S)
Forward Algorithm
\mathcal{F}(S)
Forward Algorithm
\text{Complexity: } \mathcal{O}(|S|)
Backward Algorithm - Step 1
Backward Algorithm - Step 1
\phi
\psi
(-1,3)
(-1,3)
Backward Algorithm - Step 2
Backward Algorithm - Step 2
Backward Algorithm - Step 3
Backward Algorithm - Step 3
\text{Complexity: } \mathcal{O}(q) + \mathcal{O}(\log \min(a,b)) + \mathcal{O}(\sqrt{|S|})
Step 1
Step 2
Step 3
Forward
Depends on the size of the finite set
Backward
Depends on the square root of the finite set size and the parameters of the rational rotations
Backward vs. Forward Algorithm
Backward vs. Forward Algorithm
When the size of the finite set is relatively low and the number of elements in the non-injective zones is relatively high, the forward algorithm is usually a better choice than the backward algorithm and vice versa.
Finding Local Bijectivity Angle Interval
Finding Local Bijectivity Angle Interval
\mathcal{F}(S)
Finding Local Bijectivity Angle Interval
U(S)
What are the intervals of the parameters around the initial ones such that the corresponding transformations remain bijective when restricted to the set?
Our strategy in short: Fix the translation and then find a rotation angles interval using the notion of "hinge angles".
Finding Local Bijectivity Angle Interval
Finding Local Bijectivity Angle Interval
\cos \alpha = \frac{p_1 \lambda + p_2 \left(k + \frac{1}{2} \right)}{p_1^2 + p_2^2}
\lambda = \sqrt{p_1^2 + p_2^2 - \left(k + \frac{1}{2} \right)^2}
Finding Local Bijectivity Angle Interval
Finding Local Bijectivity Angle Interval
\cos \alpha = \frac{p_1 \lambda + p_2 \left(k - t_2 + \frac{1}{2} \right)}{p_1^2 + p_2^2}
\lambda = \sqrt{p_1^2 + p_2^2 - \left(k - t_2 + \frac{1}{2} \right)^2}
Finding Local Bijectivity Angle Interval
Finding Local Bijectivity Angle Interval
Finding Local Bijectivity Angle Interval
Part II:
3D Discrete Spaces
Introduction to 3D Digital Geometry
The Cubic Grid
The cubic lattice is then:
Digitization Model
A digitization cell of
\mathbf{x}
denoted by
\mathcal{C}(\mathbf{x}).
Digitization Model
The digitization operator is defined as
\mathcal{D}: \mathbb{R}^3 \rightarrow \mathbb{Z}^3
such that
\forall \mathbf{x} \in \mathbb{R}^3, \exists! \mathcal{D}(\mathbf{x}) \in \mathbb{Z}^3
\mathbf{x} \in \mathcal{C}(\mathcal{D}(\mathbf{x})).
and
Quick Introduction to 3D Rigid Motions
\left|
\begin{array}{lllll}
\mathcal{U} & : & \mathbb{R}^3 & \to & \mathbb{R}^3 \\
& & \mathbf{x} & \mapsto & \mathbf{R} \mathbf{x} + \mathbf{t}
\end{array}
\right.
Rigid Motions on
\mathbb{R}^3
Properties
-
Do preserve distances
-
Bijective
\mathbf{R}
- rotation matrix
\mathbf{t}
- translation vector
U = \mathcal{D}\ \circ \mathcal{U}_{|\mathbb{Z}^3}
Properties
- Non-injective
- Non-surjective
- Do not preserve distances
\mathcal{U}(\mathbb{Z}^3)
Digitized Rigid Motions
Contributions in Short
- An algorithm to characterize bijective digitized rotations
- An algorithm to compute all possible images of a finite digital set under digitized rigid motions
I am Going to Talk About
An algorithm to characterize bijective digitized rotations
Spatial Rotations and Quaternions
Spatial Rotations and Quaternions
\mathbb{H} = \{a + b i + c j + d k | a,b,c,d \in \mathbb{R} \}
with
i^2 = j^2 = k^2 = i j k = {-1}
Properties:
- Hamilton product is not commutative
- Any rotation can be written as
\mathcal{U} : \mathbf{x} \mapsto q \mathbf{x} q^{-1}
where
q \in \mathbb{H}, \mathbf{x} \in \mathbb{R}^3
- We can derive a rotation matrix
where
K = a^2 + b^2 + c^2 + d^2
The figure source: http://www.3dgep.com/understanding-quaternions/
Bijectivity of 3D Digitized Rotations
Bijectivity of 3D Digitized Rotations
Remainders
3D digitized rotation is then
bijective when
\forall \mathbf{y} \in \mathbb{Z}^3\ \exists! \mathbf{x} \in \mathbb{Z}^3, S_q(\mathbf{x},\mathbf{y}) \in \mathcal{C}(\mathbf{0})
Remainders
Equivalently and more computationally friendly (we will see later)
such that
S_{q}(\mathbb{Z}^3,\mathbb{Z}^3) \cap ((\mathcal{C}(\mathbf{0}) \cup q \mathcal{C}(\mathbf{0}) q^{-1}) \setminus (\mathcal{C}(\mathbf{0}) \cap q \mathcal{C}(\mathbf{0}) q^{-1})) = \varnothing
Group Spanned by Values of
S_q
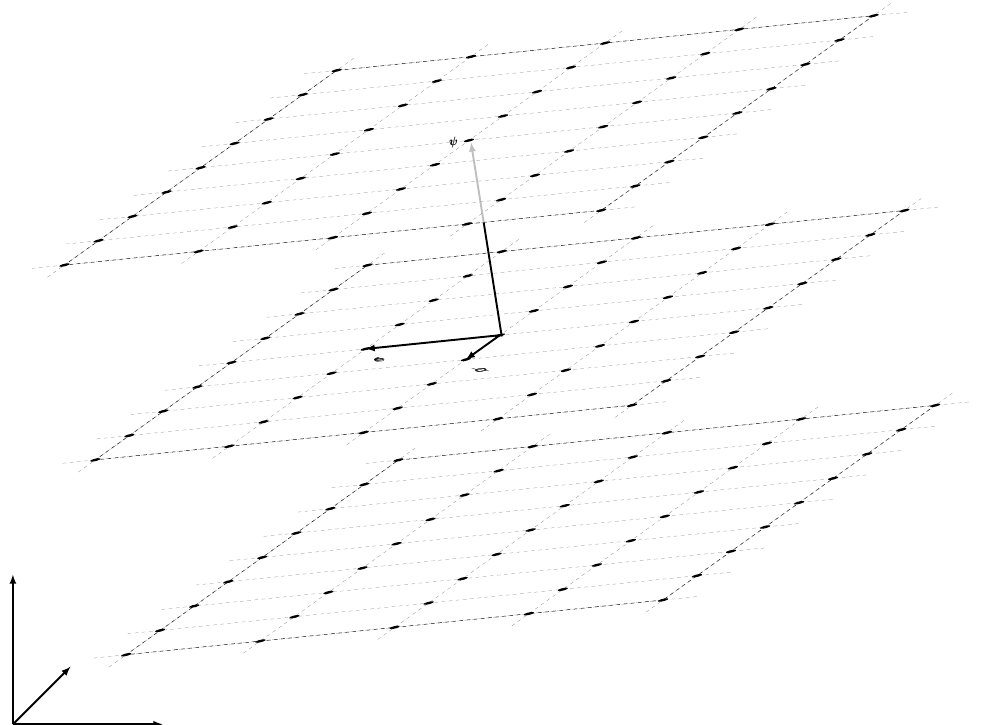
Proposition
If all the generators of
\mathcal{G}_q
have only rational terms, then there exist vectors
which are the
minimal generators of
\mathcal{G}_q.
Group Spanned by Values of
S_q
Lemma
If
\mathcal{G}_q
is dense, then the
corresponding 3D digitized rotation is not bijective.
Group Spanned by Values of
S_q
Conjecture
If
\mathcal{G}_q
has a dense factor,
the corresponding digitized rotation is not bijective.
Lipschitz Quaternions and Rational Rotations
Proposition
There is a two-to-one correspondence between the set of Lipschitz quaternions
\mathbb{L} = \{ a+ b i + c j + d k | a,b,c,d \in \mathbb{Z}\}
such that the
\gcd(a,b,c,d) = 1,
and the set of rational rotations.
where
K = a^2 + b^2 + c^2 + d^2.
\mathbf{R} =
Bijectivity Characterization Algorithm
Turning into Integers
Since we have
q \cdot \mathbf{x} \cdot q^{-1}
where
q^{-1} = \frac{\bar{q}}{|q|^2}
and
\mathcal{G}_q
is rational, we can
multiply by
|q|^2
and obtain an integer lattice.
Reducing the Left Factor
We are allowed to divide on the left by q while keeping integer valued functions.
Characterization Algorithm Step 1
To check if
\mathbf{w} \in \mathbb{Z}^4
belongs to values
of
S'_{q},
first verify whether
a w_1 - b w_2 - c w_3 - d w_4 = 0
Characterization Algorithm Step 2
Then we solve the following Diophantine system:
\mathbf{Az} = \mathbf{w}
where
\mathbf{z}^t = (\mathbf{x}, \mathbf{y}) \in \mathbb{Z}^6
and
The complexity of reducing
\mathbf{A} \text{ is } \mathcal{O}(\log^2N(\mathbf{A})).
The final complexity is
\mathcal{O}(|q|^3 + \log^2N(\mathbf{A})).
Some Experimental Results
Conclusion and Perspectives
- A general framework to study 2D digitized rigid motions
- Comparison of the digitized rigid motions defined on square and hexagonal lattices
-
Characterization of bijective digitized:
- rigid motions on the square grid
- rotations on the hexagonal grid
- 3D rotations on the cubic grid
- Algorithms to characterize if a digitized rigid motion is bijective when restricted to a finite set
- An algorithm to compute, under 3D digitized rigid motions, all possible images of a finite digital set
Conclusion
Conclusion and Perspectives
- Analytical characterization of 3D bijective rigid motions
- Extension of the study to the triangular grid
-
Identification of minimal 3D sets that break 6-connectivity under digitized rigid motions
Perspectives
Rigid Motions on Discrete Spaces
By Kacper Pluta
Rigid Motions on Discrete Spaces
Kacper Pluta's PhD defense presentation.
