week 04

Clustering and Community Detection

Social Network Analysis

03-2

Community Detection General Idea

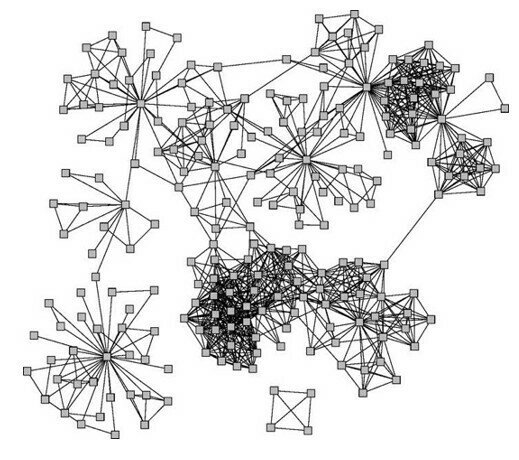
Connected and undirected graphs

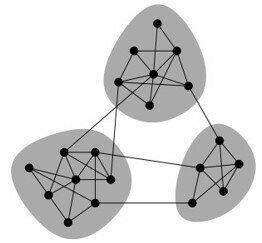
Network Communities

What makes a community (cohesive subgroup):

  • Mutuality of ties. Everyone in the group has ties (edges) to one another
  • Compactness. Closeness or reachability of group members in small number of steps, not necessarily adjacency
  • Density of edges. High frequency of ties within the group
  • Separation. Higher frequency of ties among group members compared to non-members

Wasserman and Faust

Graph cliques

A clique is a complete (fully connected) subgraph, i.e. a set of vertices  where each pair of vertices is connected.

Cliques can overlap

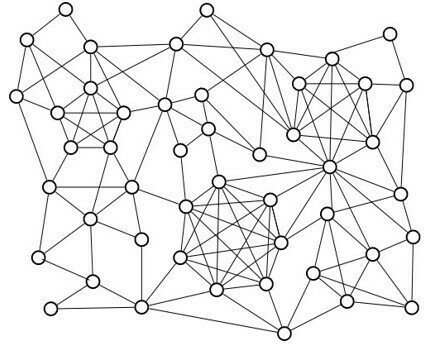
Graph cliques

  • A maximal clique is a clique that cannot be extended by including one more adjacent vertex (not included in larger one)
  • A maximum clique is a clique of the largest possible size in a given graph
  • Graph clique number is the size of the maximum clique

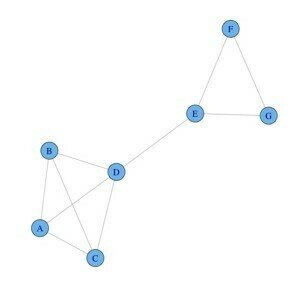
Graph cliques

Maximum cliques

Maximal cliques:

       Clique size:          2     3    4    5

Number of cliques:  11   21   2    2

Network comminities

Network communities are groups of vertices such that vertices inside the  group connected with many more edges than between groups.

Community detection is an assignment of vertices to communities.  Will consider non-overlapping communities, graph cuts

Community detection

Consider only sparse graphs m «n2  Each community should be connected  Combinatorial optimization problem:

- optimization criterion (cut, conductance, modularity)

- optimization method

Exact solution NP - hard

(bi-partition: n = n1 + n2, n!/(n1!n2!) combinations)

Solved by greedy, approximate algorithms or heuristics. Recursive top-down 2-way partition, multiway partition. Balanced class partition vs communities

recursive partitioning

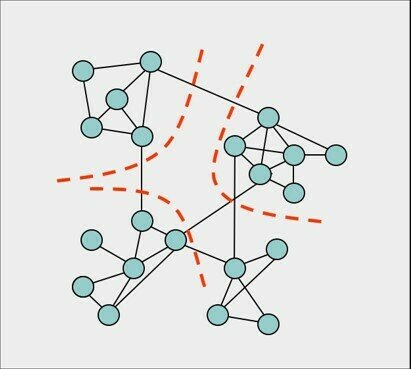
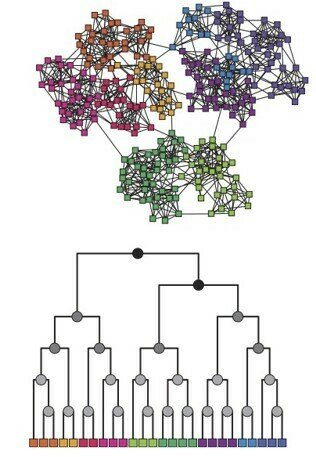
Edge betweenness

Focus on edges that connect communities.

Edge betweenness - number of shortest paths σst (e) going through edge e

Construct communities by progressively removing edges

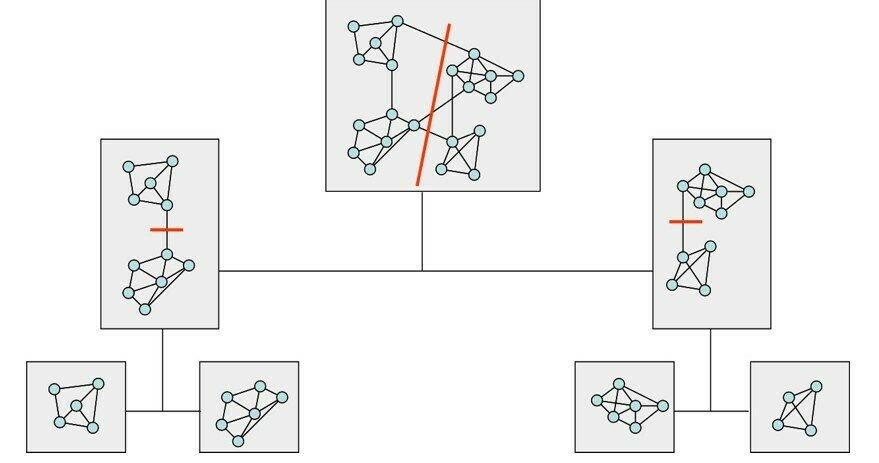
C_B(e) = \sum_{s \neq t} {\dfrac{\sigma_{st}(e)}{\sigma_{st}}}

Edge betweenness algorithm

Newman-Girvan, 2004

Algorithm: Edge Betweenness

Input: graph G(V,E)

Output: Dendrogram/communities

Repeat

          For all e ∈ E compute edge betweenness CB (e);

          remove edge ei with largest CB (ei ) ;

until edges left;

 

If bi-partition, then stop whrn graph splits in two components (check for connectedness)

Hierarchical algorithm, dendrogram

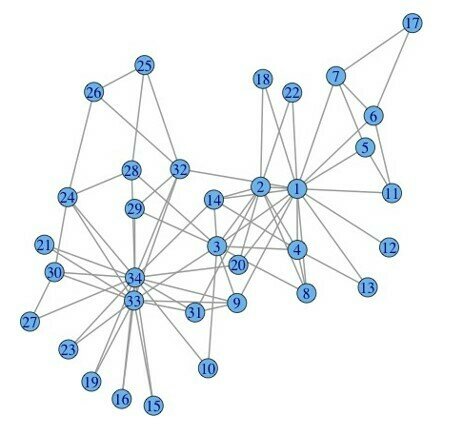
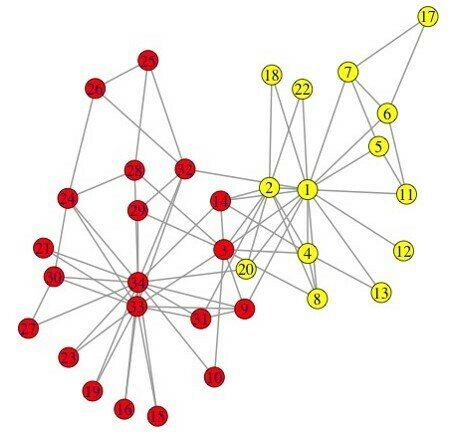
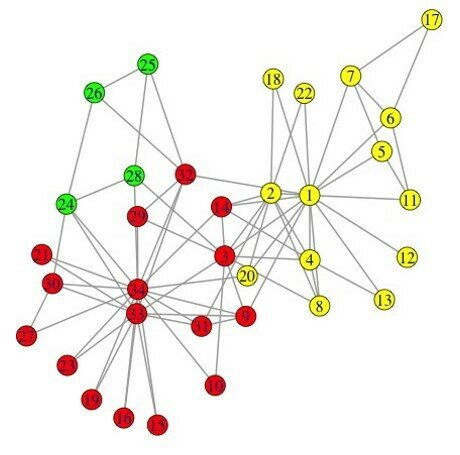
03-3

Community Detection Quality

  • Various goodness metrics that evaluate structural properties of communities.
  • Density - fraction of internal edges out of total number of possible edges.
  • Conductance - fraction of total edge volume that points outside the cluster.
  • Modularity - the difference of the number of edges in a community and the expected number of edges (assuming you have an identical degree distribution).

Community Detection Metrics

Fortunato, Newman, 20 years of network community detection, Nature Physics, 2022, [pdf]

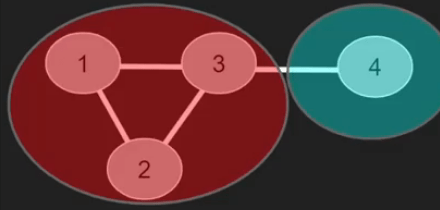
Metric: Density

D(S) = \dfrac{2E_s}{|S|(|S|-1)}
D({1,2,3,4}) = \dfrac{2\times5}{4(4-1)} = \dfrac{10}{12}

Example:

Metric: Conductance

C(S) = \dfrac{O_s}{2E_s+O_s}
C(S) = \dfrac{3}{2\times5+3} = \dfrac{3}{13}

Example:

Measure of internal and external connectivity. The fraction of edges pointing outside a community

Metric: Modularity

  • A global metriic: defined per-network, not per-community
  • Measure of internal and external connectivity. How well network partitions into modules
  • Higher values are better
\mathbb{Q}(\mathbb{C}) = \dfrac{1}{2|E|}\sum_{u,v \in V}\left(A_{u,v}-\dfrac{d_u d_v}{2|E|}\right)\delta(\mathbb{C}_u\mathbb{C}_v)
\dfrac{1}{2|E|} -

normalize by degree sum

\sum_{u,v \in V}(A_{u,v}-\dfrac{d_u d_v}{2|E|}) -

sum goes through every pair of verticies

\delta(\mathbb{C}_u\mathbb{C}_v) -

Kronecker delta function == 1 only if u and v are in the same community

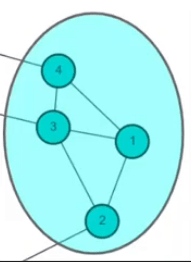
Metric: Modularity

v=1 v=2 v=3 v=4
u = 1 (0 - (2*2)/8)*1 (1 - (2*2)/8)*1 (0 - (2*1)/8)*0
u = 2 (1 - (2*2)/8)*1 (0 - (2*2)/8)*1  (1 - (2*3)/8)*1  (0 - (2*1)/8)*0
u = 3 (1 - (3*2)/8)*1  (0 - (3*3)/8)*1 
u = 4 (0 - (1*2)/8)*0 (0 - (1*2)/8)*0 (0 - (1*1)/8)*1

Q = 1/8 * (...+...+...)=-0.031

\mathbb{Q}(\mathbb{C}) = \dfrac{1}{2|E|}\sum_{u,v \in V}\left(A_{u,v}-\dfrac{d_u d_v}{2|E|}\right)\delta(\mathbb{C}_u\mathbb{C}_v)

Modularity - Values

  • Modularity bounded in range [-0.5, 1]
  • All nodes in a single community or all nodes in their own community \( \rightarrow Q=0 \)
  • Nonzero values represent deviations from randomness (for better or worse)
  • values > 0.3 is an indicator of good community structure

Modularity - Another Equation

\mathbb{Q}(\mathbb{C}) = \dfrac{|E(c)|}{2|E|} - \left(\dfrac{\sum_{u \in c}d_v}{2|E|}\right)^2
\mathbb{Q}(\mathbb{C}) = \dfrac{1}{2|E|}\sum_{u,v \in V}\left(A_{u,v}-\dfrac{d_u d_v}{2|E|}\right)\delta(\mathbb{C}_u\mathbb{C}_v)
=

Modularity: Directed and Weighted

\mathbb{Q}(\mathbb{C}) = \dfrac{1}{|E|}\sum_{u,v \in V}\left(A^o_{u,v}-\dfrac{d^o_u d^i_v}{|E|}\right)\delta(\mathbb{C}_u\mathbb{C}_v)
\mathbb{Q}(\mathbb{C}) = \dfrac{1}{2|W_E|}\sum_{u,v \in V}\left(A_{u,v}-\dfrac{d^w_u d^w_v}{2|E|}\right)\delta(\mathbb{C}_u\mathbb{C}_v)

Weighted:

Directed:

  • \( o \) - outgoing edges
  • \( i \) - ingoing

Modularity score

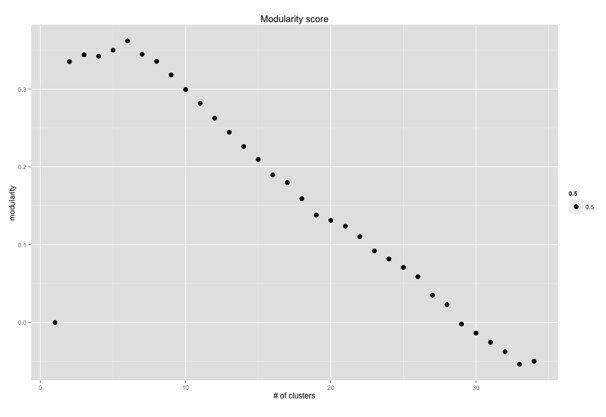
03-4

Modularity Maximization Heuristics

Modularity Maximization Heuristics

Input

Desired

output

Spectral modularity maximization

Newman, Finding community structure in networks using the eigenvectors of matrices, 2006

  • Algorithm: Spectral modularity maximization: two-way partition
  • Input: adjacency matrix \( A \)
  • solve for maximal eigenvector \( Bx = \lambda x \) ;
  • set \( s= sign(x )_{max} \)

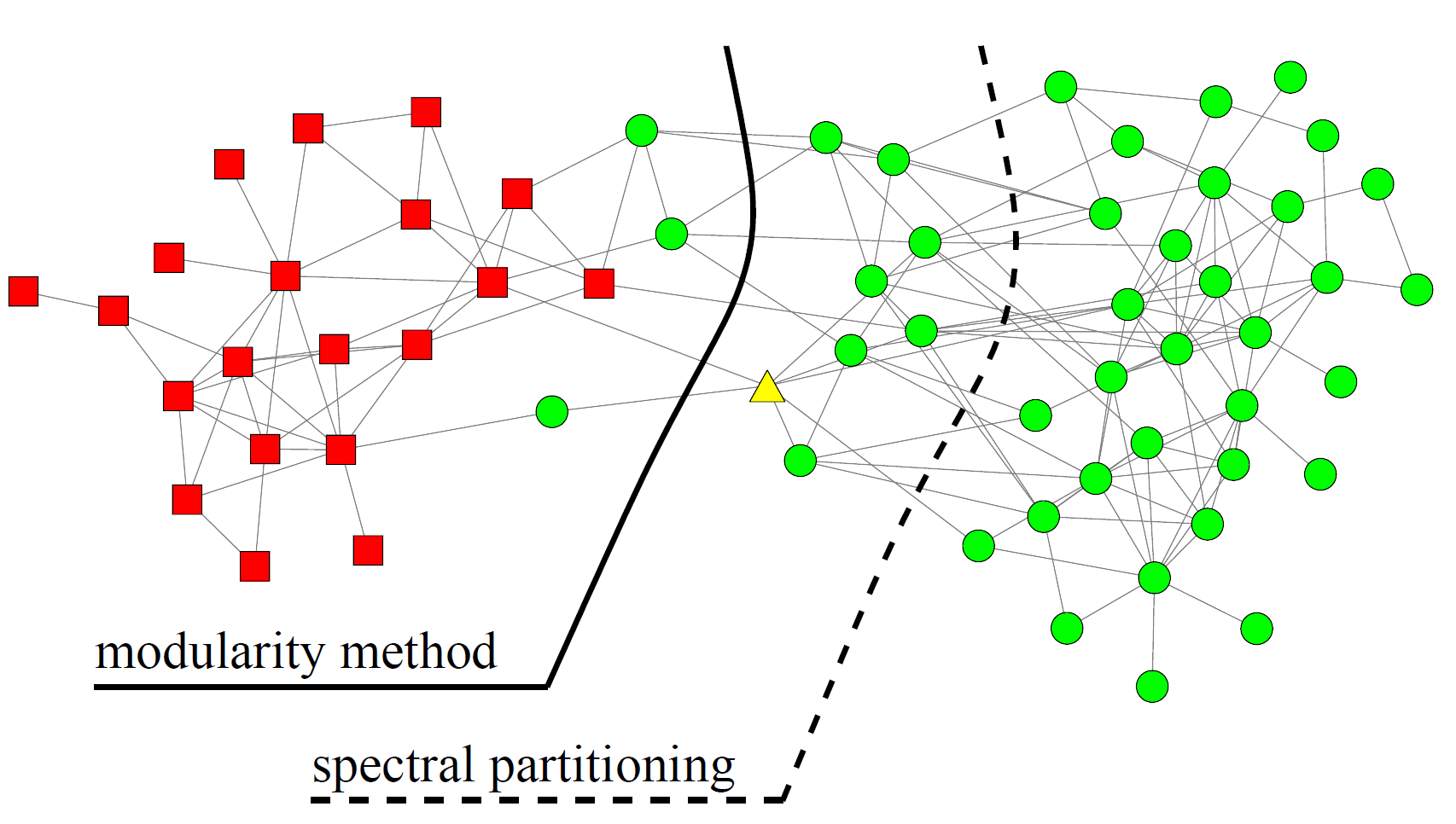
clusters = 5, modularity = 0.437

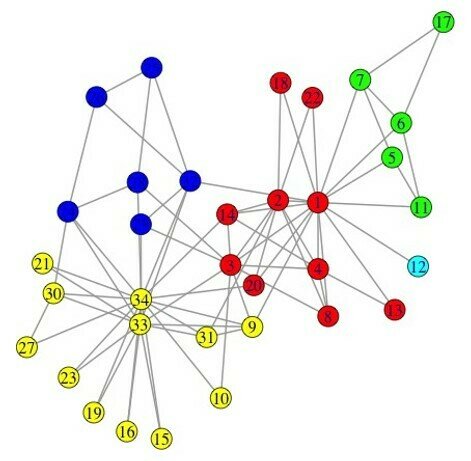
The Louvain method

  • Heuristic method for greedy modularity  optimization
  • Find partitions with high modularity
  • Multi-level (multi-resolution) hierarchical scheme
  • Scalable

Blondel, Fast unfolding of communities in large networks, 2008

The Louvain method: 1st phase

  • Put each node in a graph into a distinct community (one node per community)
  • For each node \( i \), the algorithm performs two calculations:
    • compute the modularity delta \( (\Delta Q) \) when putting node \( i \) into the community of some other neighbour \( j \)
    • Move \( i \) to a community of node \( j \) that yelds the largest gain in \( \Delta Q \)

Fast community unfolding algoritm

Algorithm: Fast unfolding

Input: Graph \( G(V,E) \)

Output: Communities

Assign every node to is own community:

repeat

      repeat

           

 

 

       until no more improvement (local max of modularity):

       Nodes from communities merged into "super nodes":

       Weight on the links added up

 until no more changes (max modularity):

For every node evaluate the modularity delta \( (\Delta Q) \) when putting node \( i \) into the community of some other neighbour \( j \);
Move \( i \) to a community of node \( j \) that yelds the largest gain in \( \Delta Q \).

Phase 1: Partitioning

\Delta Q(D \rightarrow i \rightarrow C ) = \Delta Q(D \rightarrow i) + \Delta Q(i \rightarrow C)
\Delta Q(D \rightarrow i)

Removing \( i \) from \( D \)

\Delta Q(i \rightarrow C)

Merging \( i \) into \( C \)

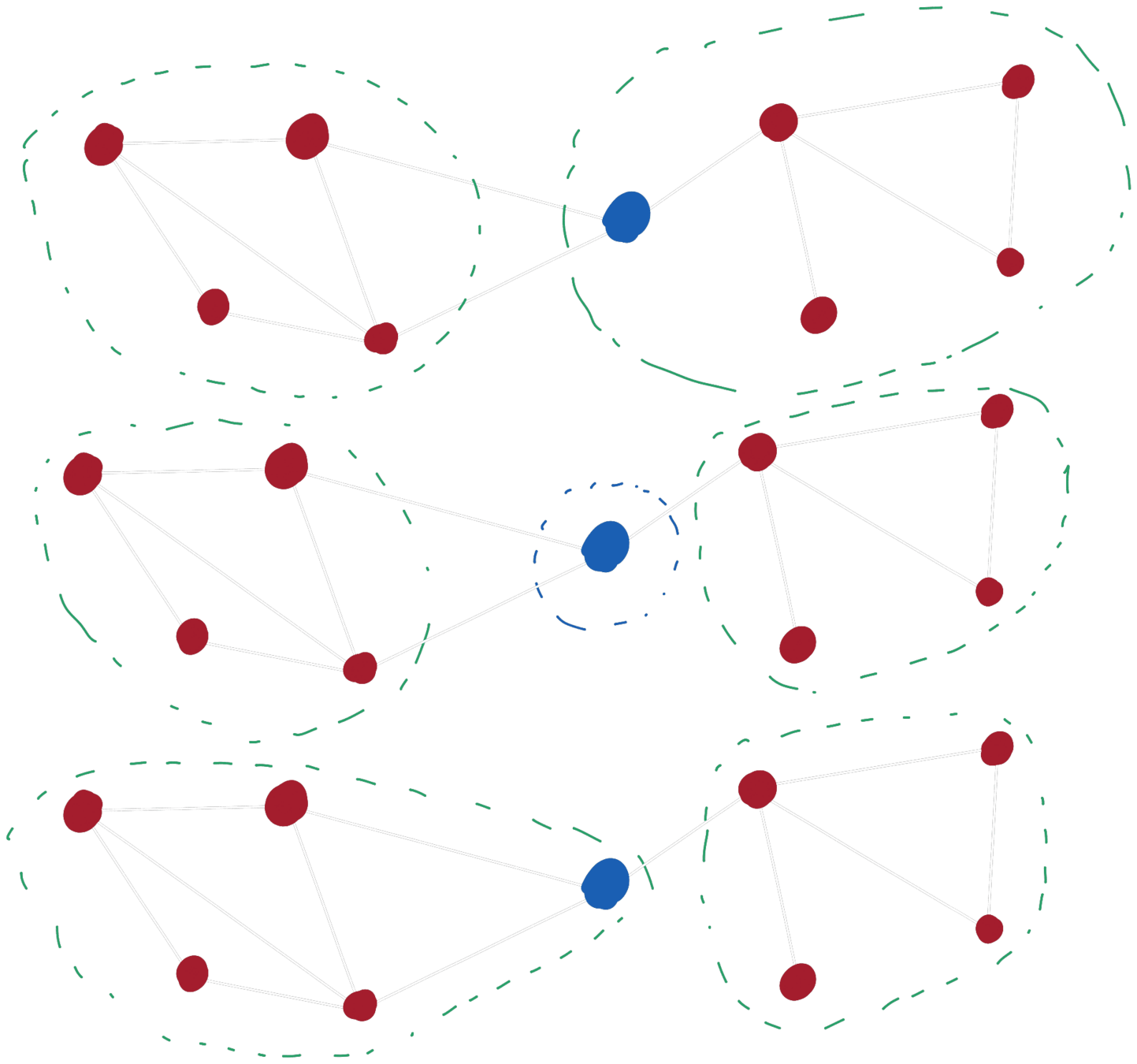
Before

Intermediate

After

\( D - i \)

\( D - i \)

\( C + i \)

\( C \)

\( D \)

\( C \)

\( i \)

\( i \)

\( i \)

Phase 2: Summary

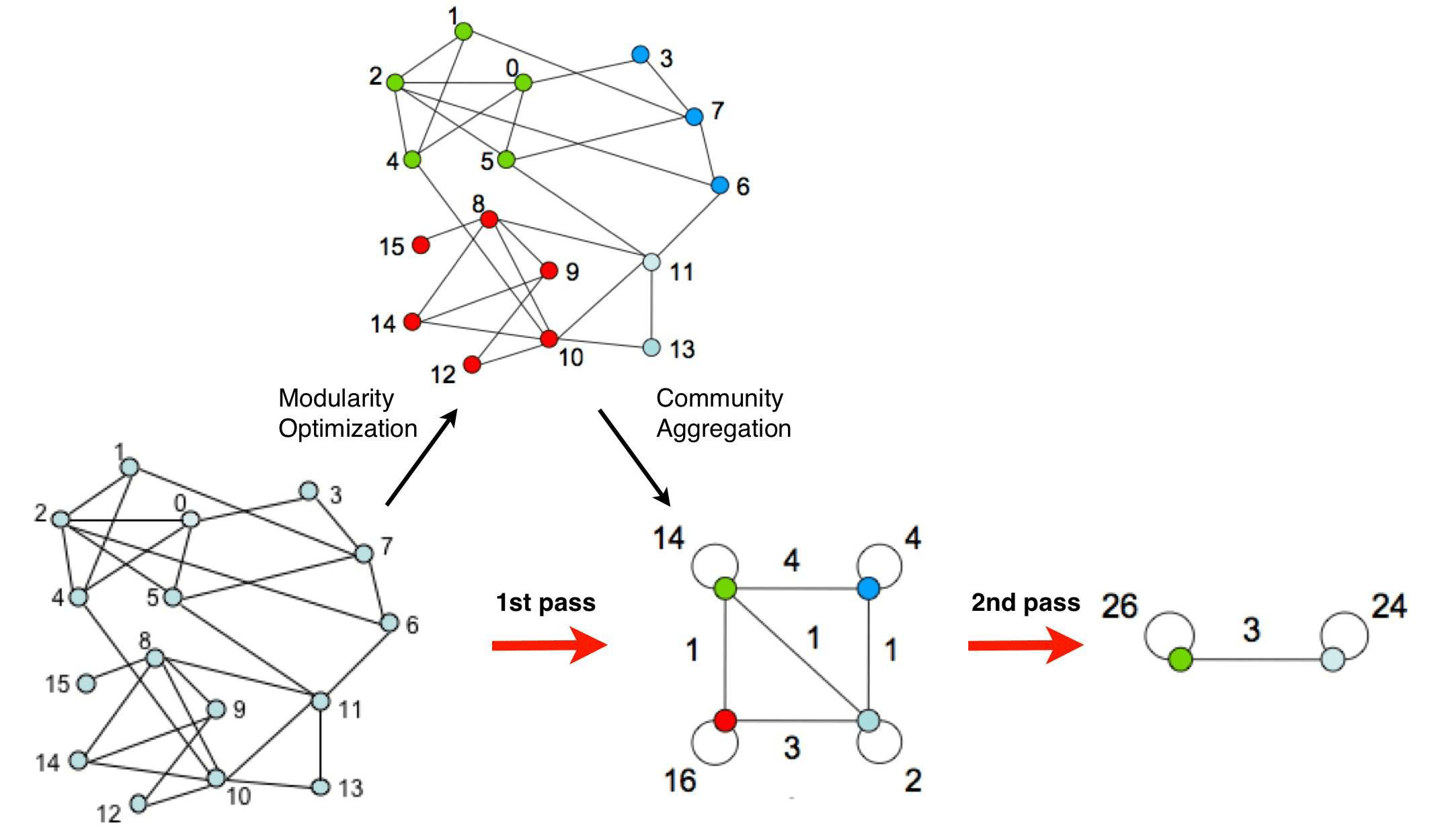
Each pass is made of two phases:

  • one where modularity is optimized by allowing only local changes of communities;
  • one where the found communities are aggregated in order to build a new network of communities. The passes are repeated iteratively until no increase of modularity is possible.

best: clusters = 6, modularity = 0.345

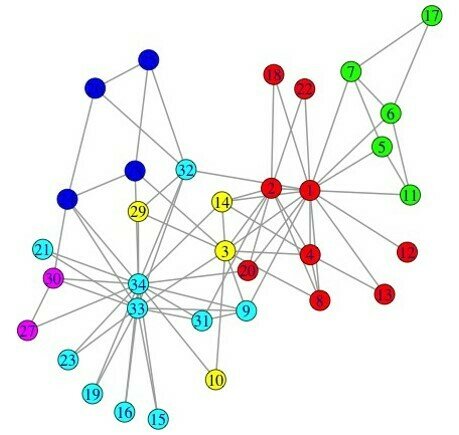
03-5

Exact/Approximate Modularity Maximization

Exact/Approximate Modularity Maximization

Input

Desired

output

Modularity-Maximizing Graph Communities via Mathematical Programming

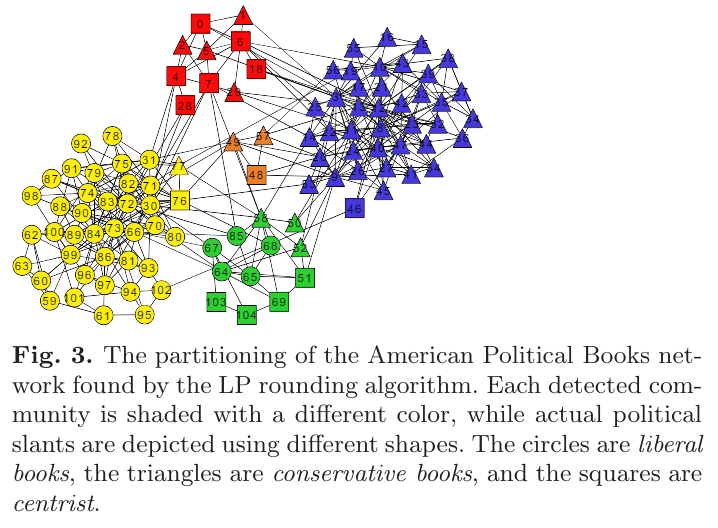
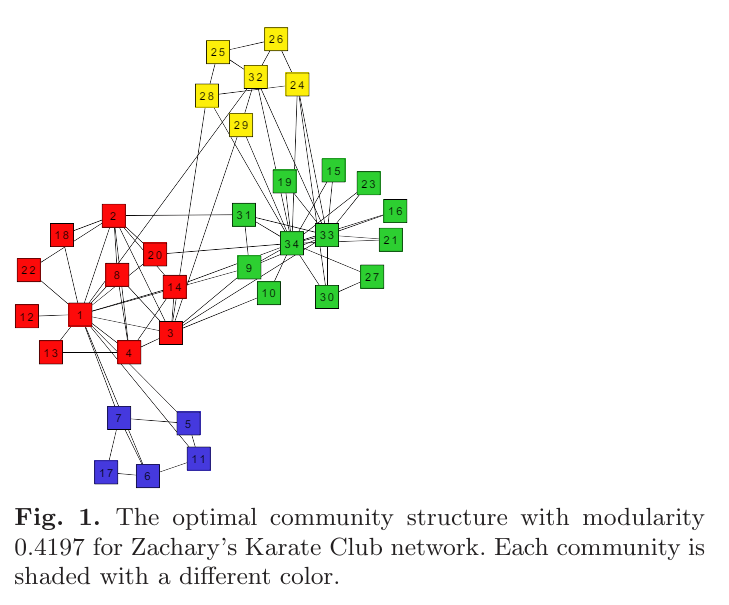
Bayan algorithm

https://github.com/saref/bayan

03-6

Other Community Detection Algorithms

Other Methods

  1. Kernigan-Lin bisection (Kernigan and Lin 1970)
  2. RB Potts model with
  3. Chinese whispers
  4. Walktrap
  5. k-cut
  6. Asynchronous label propagation
  7. Infomap
  8. Genetic Algorithm
  9. Semi-synchronous Label propagation
  10. Constant Potts Model (CPM)

Other Methods

  1. Significant scales
  2. Stochastic Block Model SBm)
  3. SBM with Monte Carlo Markov Chain
  4. WCC
  5. Surprise
  6. Diffusion Entropy Reducer
  7. GemSec
  8. Bayesian Planted Partition
  9. Markov Stability

Input

Desired

output

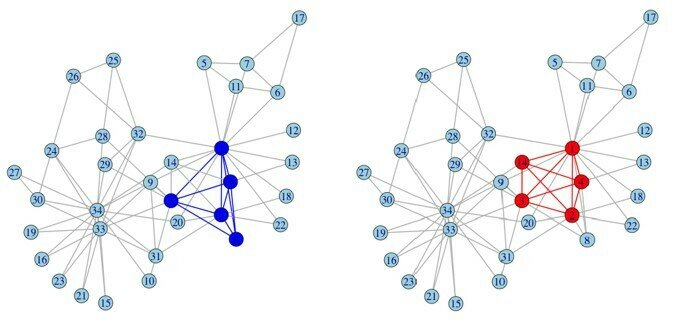
Label propagation algorithm

​Input: Graph G (V,E)

Output: Communities

Initialize labels on all nodes:

Randomized node order:

repeat

          For every node replace its label with occurring with the highest

             frequency among neighbors (ties are broken uniformly randomly);

until  every node has a label that the maximum number of the neighbors have;

Raghavan, Near linear time algorithm to detect community structures in large-scale networks, '07

clusters = 3, modularity = 0.435

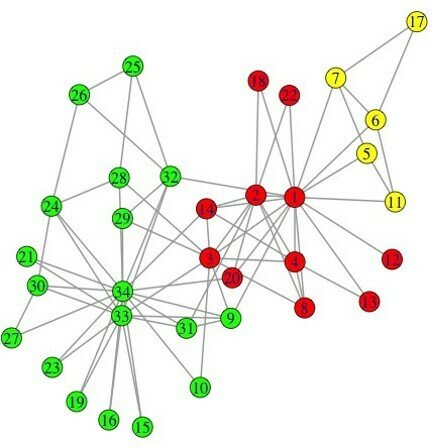
clusters = 4, modularity = 0.445

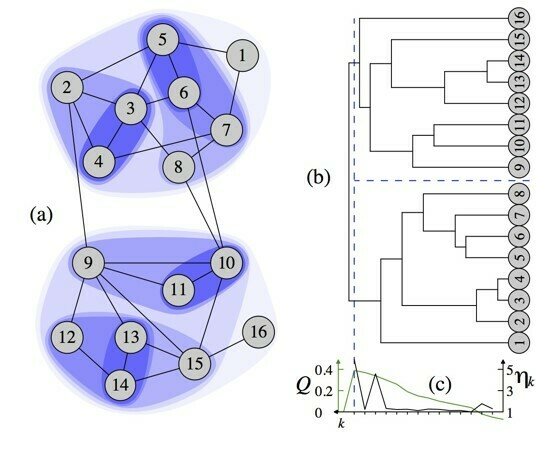
Walktrap

Algorithm: Walktrap community detection

Input: Graph G(V,E)

Output: Dendrogram/communities

Assign each vertex to its own community:

Compute random walk distance between adjacent vertices:

for n-1 steps do

           choose two "closest" communities and merge them:

           update distance between communities

ens

P. Pons and M. Latapy, 2006

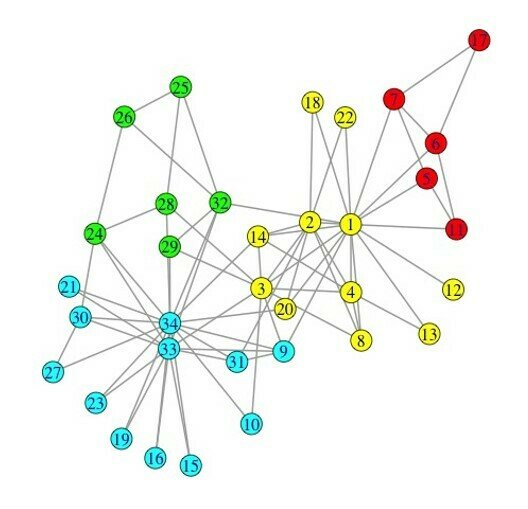
clusters = 4, modularity = 0.440

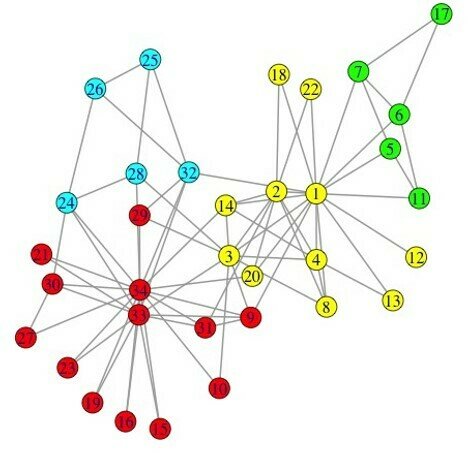
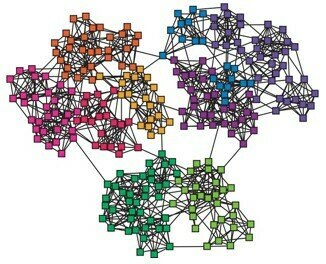
Community detection:

Graph partitioning(sparse cuts)

Vertex clustering (vertex similarity)

image from W. Liu , 2014

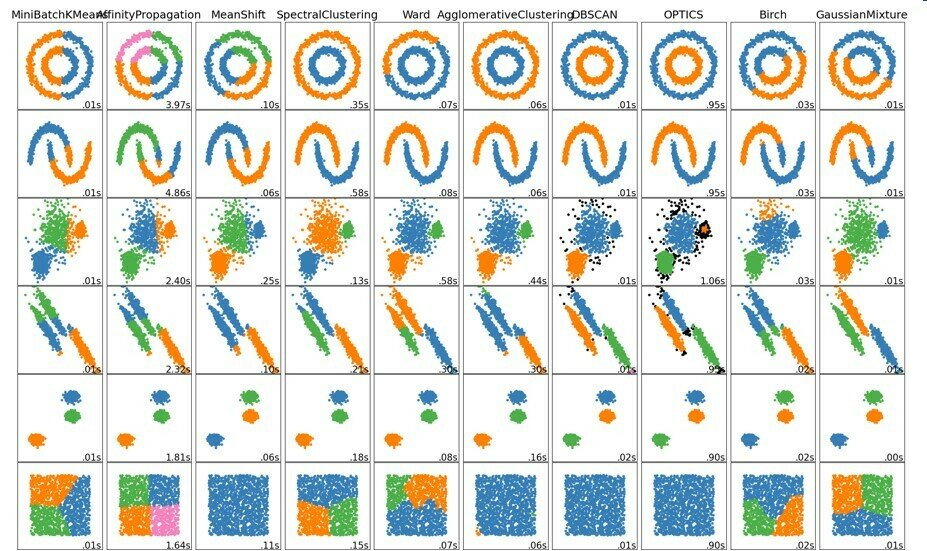
Clustering methods

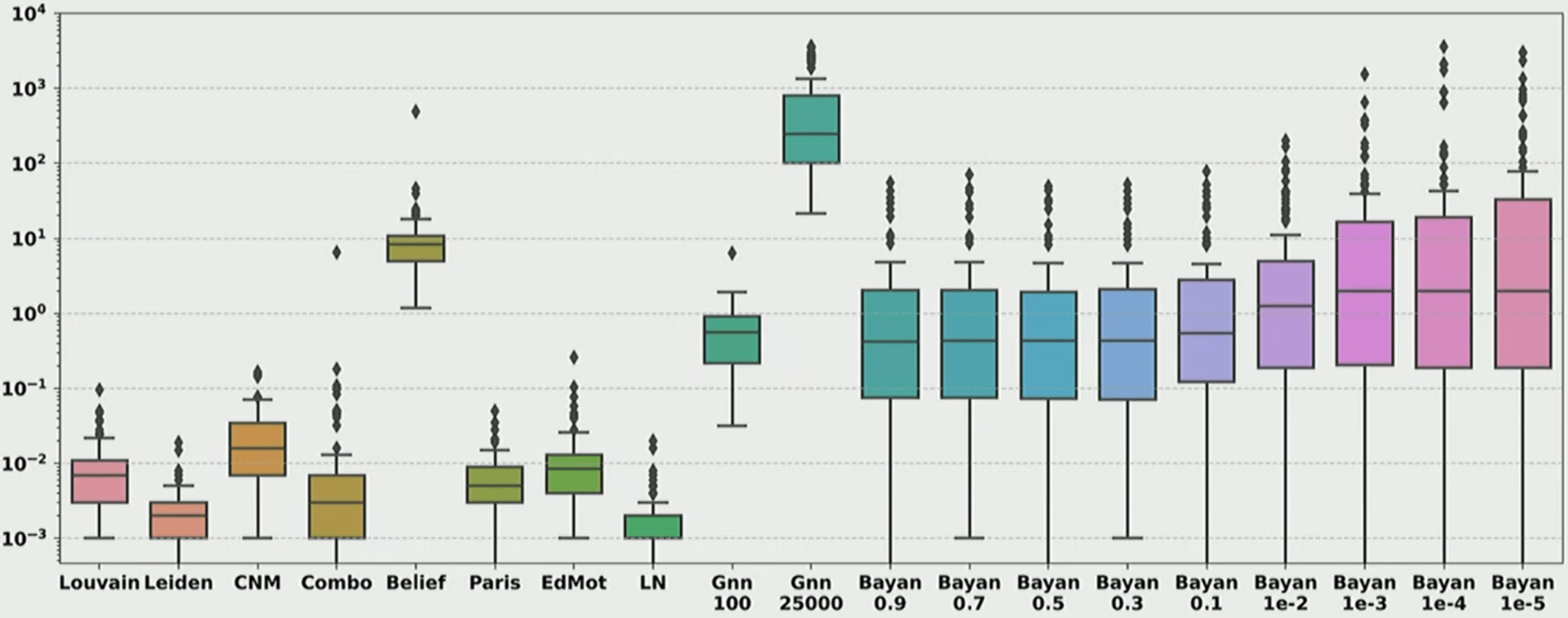
Takeaway

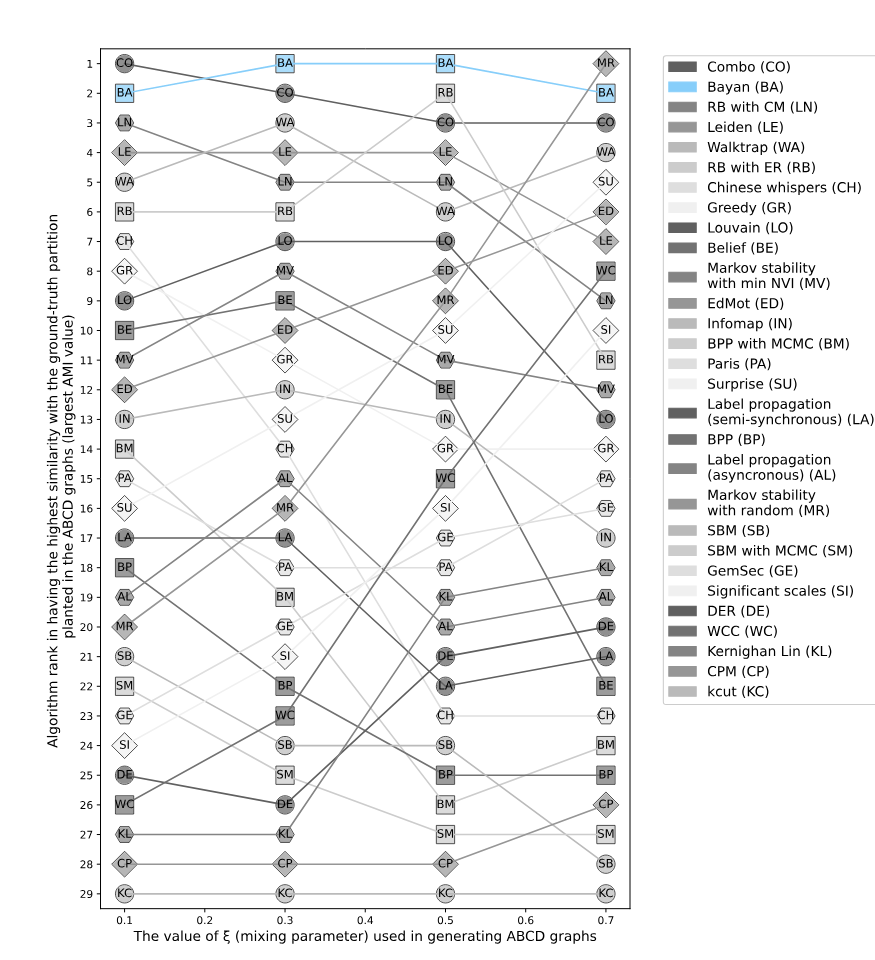
  • Heuristic modularity maximization algorithms rarely maximize modularity
    • ​Only 19.4%-43.9% of the times on synthetic and real networks
  • Suboptimal partitions of heuristic algorithms are disproportionately dissimilar to any optimal partition

Temporal community Detection

  1. Global:                                                                                    
  • Community Detection from scratch and match
  • Dependent or Temporal Trade - off Community Detection
  • Simultaneous or Offline Community Detection
  • Online Community Detection in fully Temporal Networks and in growing Temporal Networks
  1. Local: Community Detection in Temporal Networks using Seed Nodes

State-of-the-Art in Community Detection in Temporal Networks (2022)

References

Contest 1

3 prizewinners:

  • first 10
  • second, third 9
  • Modularity > strong baseline (0.657) = 8
  • Modularity > weak baseline (0.65) = 6
  • Any solution = 4
  • 1 submission per day.
  • All submission's are supposed to be supported with code.
  • The code should reproduce declared Modularity in 6/10 starts with different random seeds.

Deadline:

- 10 October (AoE)

- best solutions are supposed to be discussed 17 October

deck

By karpovilia

Made with Slides.com

deck

  • 197

More from karpovilia