week 07

Graph Neural Networks

Social Network Analysis

Message Passing

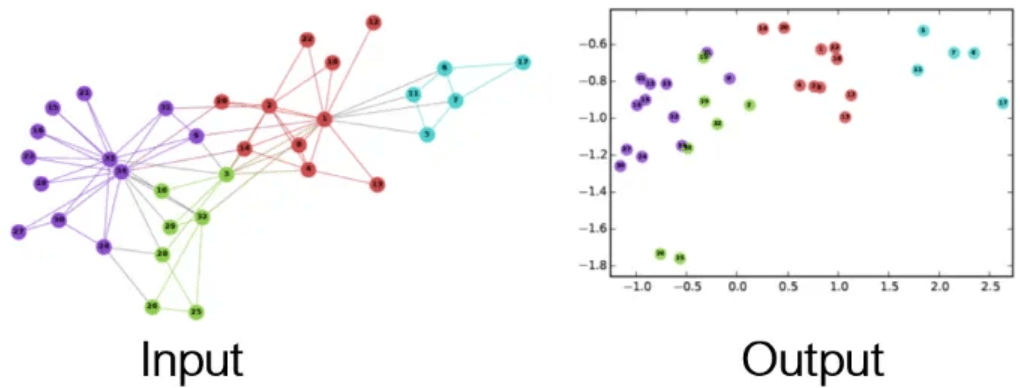
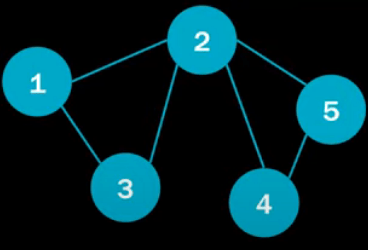
  • Our goal is to assign our nodes meaningful coordinates (embeddings)

coordinates allow us to create decision boundaries for classification problems

  • An embedding of a node should consider it's connections

i,e, nodes that share many connections should have similar embeddings

Why

Example

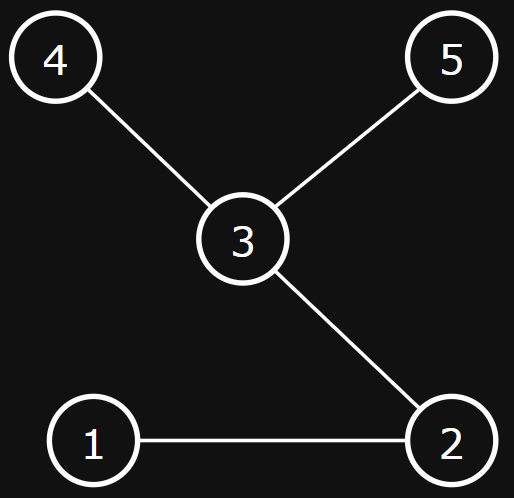
  • Nodes: people
  • Node features: age, net worth
  • Edges: in phone contacts
  • Edge features: number of phone calls in last year

Intuition

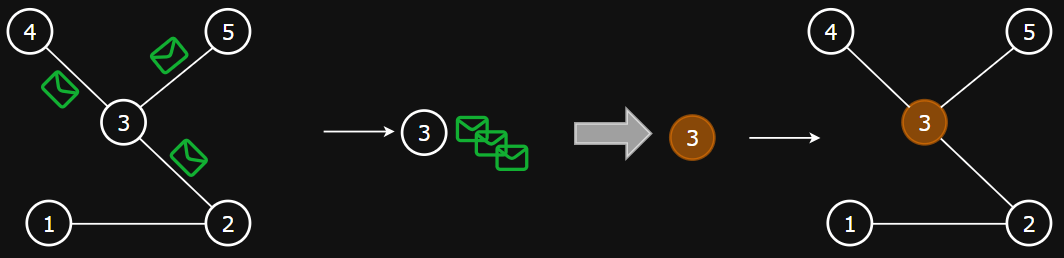
  • Goal: to calculate neighborhood-aware embeddings for nodes
  • Approach:
  • Messages are sent between nodes via the edges
  • Nodes use these messages to update its embedding

Framing the problems

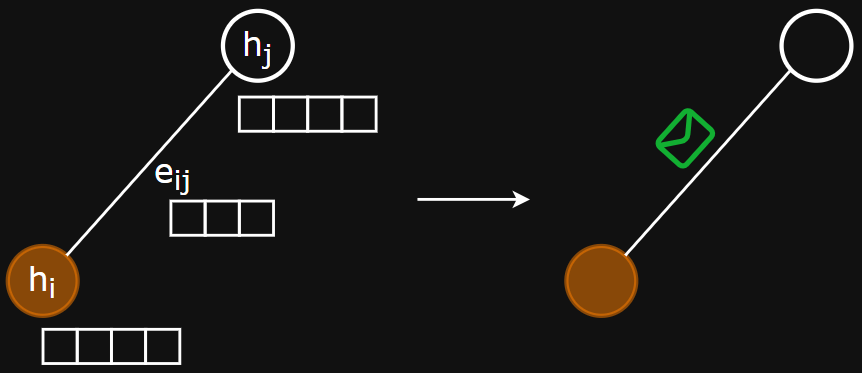
  • Message function - computes the message using node/edge features
  • Aggregation function - combines the set of messages into a fixed-length vector that represents the neighbourhood
  • Update function - computes new node embeddings using aggregated messages and the old node embedding

Message function

m_{i, j}^{(k)}=M\left(h_i^{(k)}, h_j^{(k)}, e_{i j}\right)
M\left(h_i^{(k)}, h_j^k, e_{i j}^{k)}\right) \longrightarrow

Graph Attention Networks [link]  [pdf]

Message function examples

\begin{aligned} & m_{i, j}^{(k)}=M\left(h_i^{(k)}, h_j^{(k)}, e_{i j}\right) \\ & m_{i, j}^{(k)}=h_j^{(k)}-\text { Neighbor copy } \\ & m_{i, j}^{(k)}=\frac{h_j^{(k)}}{\left|N_j\right|}-\text { Normalized neighbor copy } \\ & m_{i, j}^{(k)}=\alpha\left(h_i^{(k)}, h_j^{(k)}\right) h_j^{(k)}-\text { Attention } \end{aligned}

Aggregation function

\hat{m}=\bigoplus{j \in N_i} m_{i, j}^{(k)}

aggregate all the messages from the neighborhood of i

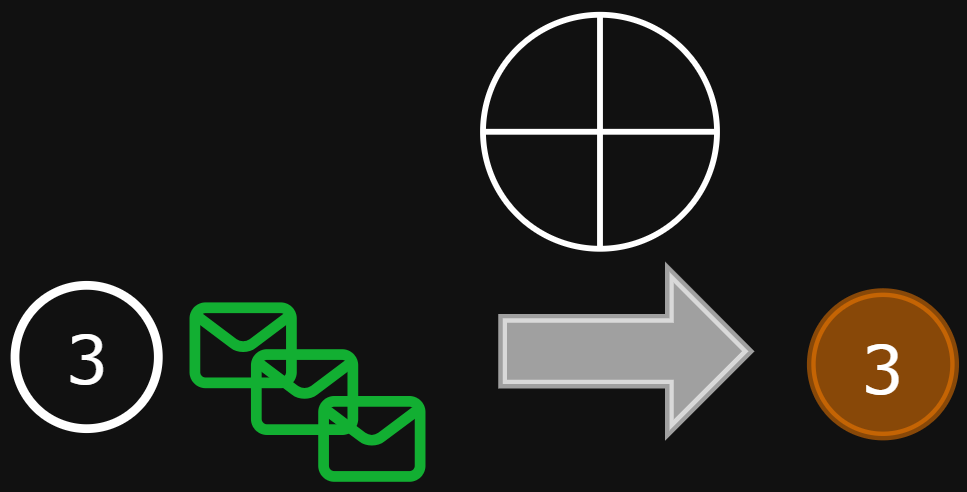
Aggregation function properties

  • Fixed-lentgh representation regardless of neighborhood size
  • Permutation invariant: gives the same answer regardless of how you order the inputs

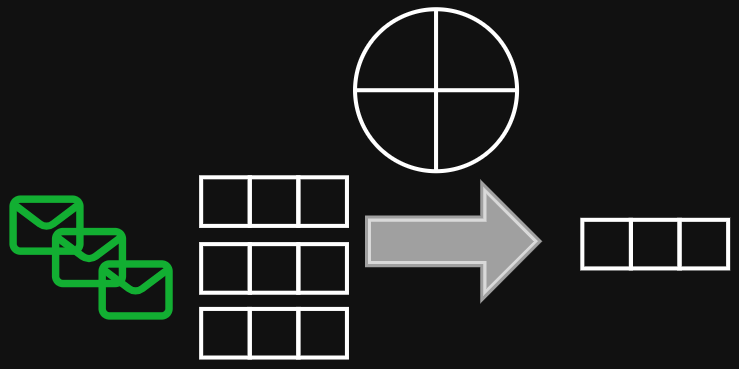
Aggregation function examples

\hat{m}_{i, j}^{(k)}=\oplus m_{i j}^{(k)}
\hat{m}_{i, j}^{(k)}=\sum_{j \in N_i} m_{i j}^{(k)} \quad \text {- Sum }
\hat{m}_{i, j}^{(k)}=\frac{1}{\left|N_i\right|} \sum_{j \in N_i} m_{i j}^{(k)} \text { - Average }
\hat{m}_{i, j}^{(k)}=\max _{j \in N_i} m_{i j}^{(k)} \quad-\text { Max }

Update function

h_i^{(k+1)}=\varphi\left(h_i^{(k)}, \hat{m}_i^{(k)}\right)

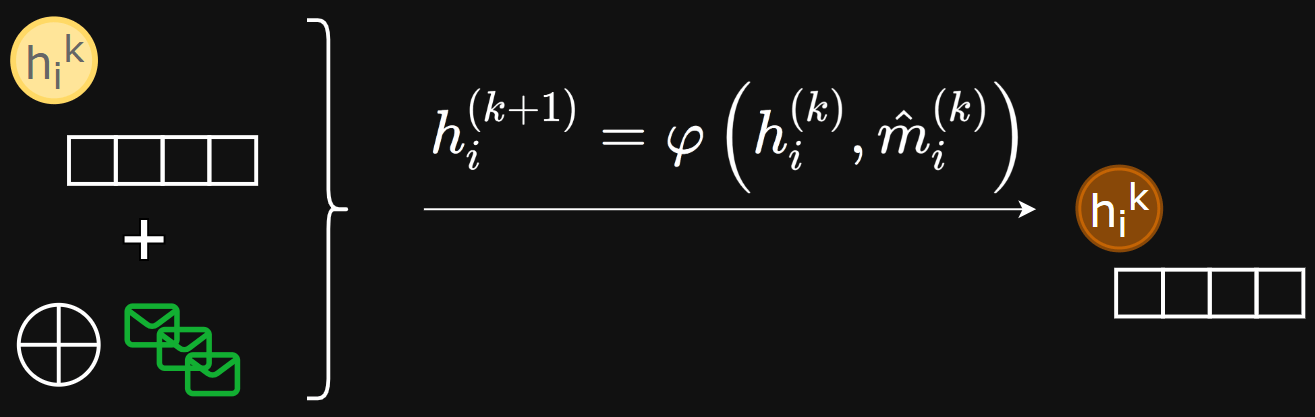
Update function examples

h_i^{(k+1)}=\varphi\left(h_i^{(k)}, \hat{m}_i^{(k)}\right)
h_i^{(k+1)}=\sigma\left(W^{(k+1)}, \hat{m}_i^{(k)}\right)
h_i^{(k+1)}=\sigma\left(W_{\text {self }}^{(k+1)} h_i^{(k)}+W_{n e i g h}^{(k+1)} \hat{m}_i^{(k)}+b^{(k+1)}\right)
h_i^{(k+1)}=\sigma\left(W^{(k+1)}, \operatorname{CONCAT}\left(h_i^{(k)} \hat{m}_i^{(k)}\right)\right)

Architecture examples - GCN

h_i^{(k+1)}=\sigma\left(W^{(k+1)}, \hat{m}_i^{(k)}\right)
\hat{m}_{i, j}^{(k)}=\sum_{j \in N_i} m_{i j}^{(k)}=\sum_{j \in N_i} \frac{1}{c_{i j}} h_j^{(k)}
h_i^{(k+1)}=\sigma\left(W^{(k+1)} \sum_{j \in N_i} \frac{1}{c_{i j}} h_j^{(k)}\right)

Examples in code - GraphSage

h_i^{(k+1)}=\sigma\left(W^{(k+1)} C O N C A T\left(h_i^k, \frac{1}{\left|N_i\right|} \sum_{j \in N_i} h_j^{(k)}\right)\right)

SAGEConv [link]

Message passing and reducing [link]

Graph Attention Networks

Examples

Examples

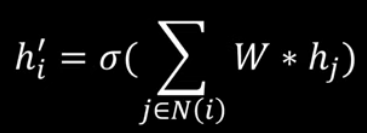
Examples

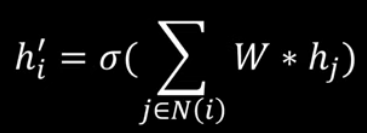
Examples

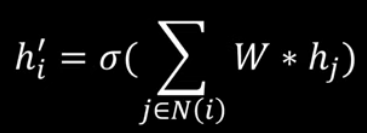
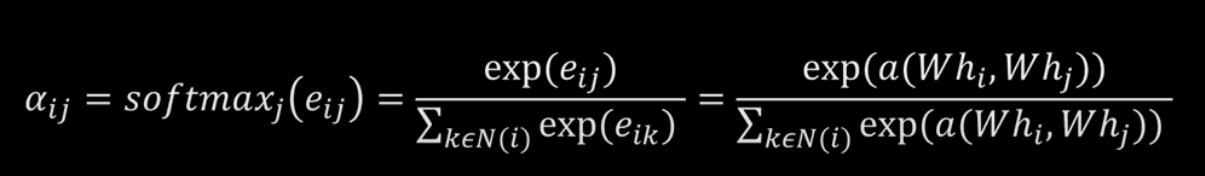
Graph Classification and Regression Overview

Examples

  • Predict if this molecule:
  • Is toxic
  • Activates a protein / Treats a disease
  • General properties of molecules
  • Predict the biological taxonomy of a protein interaction network
  • What type of object a point cloud represents
  • The expression made by a face, represented as a mesh

Overall Architecture

  • Input features X for nodes and edges, when available
  • OPTIONAL: Preprocess features by passing through an MLP, shared across the nodes 
  • Stack GNN layers to incorporate graph neighborhood information and get node embeddings
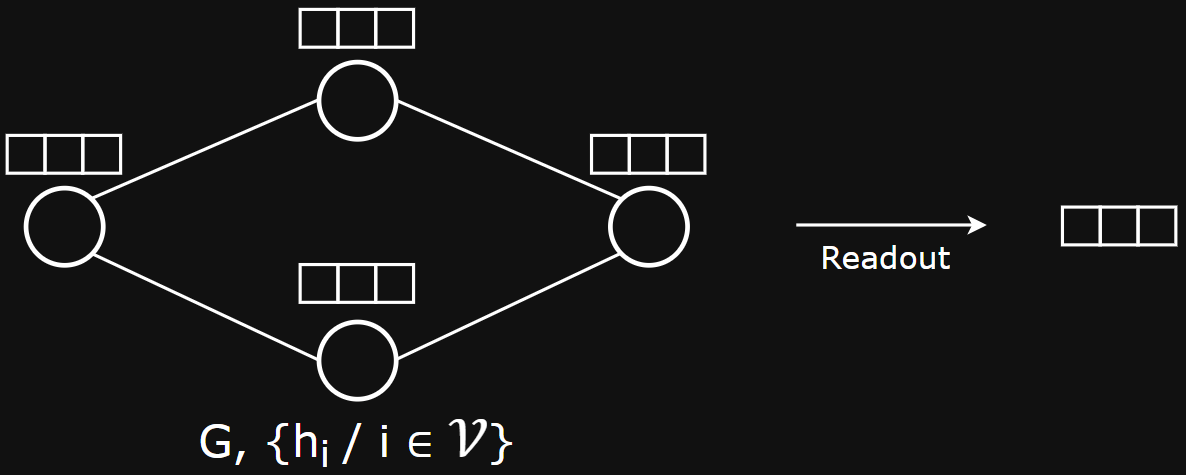
  • Use a Readout function to pool node-level embeddings into a graph-level embedding 
  • Use the graph-level embedding to make a prediction (e.g., with an MLP) on the graph
  • Loss functions are the standards: cross-entropy for classification tasks, mean-squared error for regression

Graph Pooling

Graph Pooling with Set Pooling

  • Set pooling: map a set of embeddings to a single embedding
  • I.e.,
\left\{h_i \mid i \in V\right\} \rightarrow h_G
  • Does not consider graph topology
  • Sets do not have a natural order and the operation should therefore be Permutation Invariant
  • Can use the same Permutation Invariant functions we used when creating node-neighborhood representations in GNNs: aggregation functions like SUM, MEAN, MAX, …, etc. 
  • E.g.,
h_G=\sum_{i \in V}h_i

Graph Pooling with Coarsening

  • Iteratively down-samples, typically by clustering nodes and representing the cluster by a single embedding 
  • For each iteration, the adjacency matrix is changing
  • Clustering operation needs to be differentiable so operation can be used end-to-end
  •  E.g. Graph U-Nets which projects nodes into 1-dimension using learnable linear layer and chooses k-largest ones as subset for next iteration.

H. Gao, S. Ji: Graph U-Nets [link]

Nuances of Graph Batching 

  • In previous tasks, we had one large graph and were sampling nodes and their k-hop neighborhoods 
  • Now: 1 sample = 1 full graph, no edges between graphs in the batch 
  • How should we do message passing? 
  • Could loop over each graph and run MP separately (slow)

The batched “super-graph”

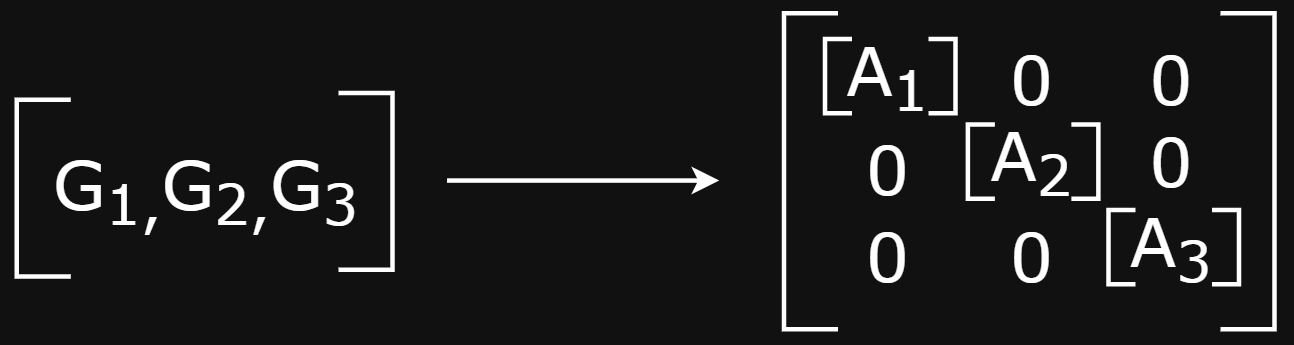
  • Alternatively, could create a “super-graph” that creates a block-diagonal adjacency matrix of disconnected components and run MP once (fast)  
  • This creates book-keeping complexity of keeping track of which node belongs to which graph. This is important when need to do graph pooling to get graph-level embeddings 
  • This is DGL’s approach and they provide tooling for managing this complexity (e.g., Batching and Reading Out Ops)

Batching and Reading Out Ops [link]

The batched “super-graph”

Graph Classification Exercise 

  • ogbg-molhiv [link]  dataset from Open Graph Benchmark: 
  • Predict whether a molecule (graph) inhibits HIV replication
  • 41k molecules from MoleculeNet [link]
  • Average of 26 nodes and 28 edges per graph
  • Natural features for both atoms (nodes) and bonds (edges):
  • Categorical in nature and the features are therefore integers that indicate the category mapping for each column
  • List of features is here, but include things like atomic number, bond type, …, etc.
  • OGB provides classes for converting these categorical/integer features into embeddings: AtomEncoder [link] and BondEncoder [link]
  • Split into train/val/test based on molecular structure
  • To evaluate generalization, the test nodes have structural differences from those in the training set

Practice in DGL

  • Started as research project out of NYU Shanghai
  • Joined forces with AWS and is now developed/maintained there in collaboration with NVIDIA and the open source community
  • Differentiated by speed and scalability
  • Supports multi-GPU and multi-machine with multi-GPU
  • Documentation has nice section of tutorials for learning and there are many examples in github
  • Backend is framework agnostic

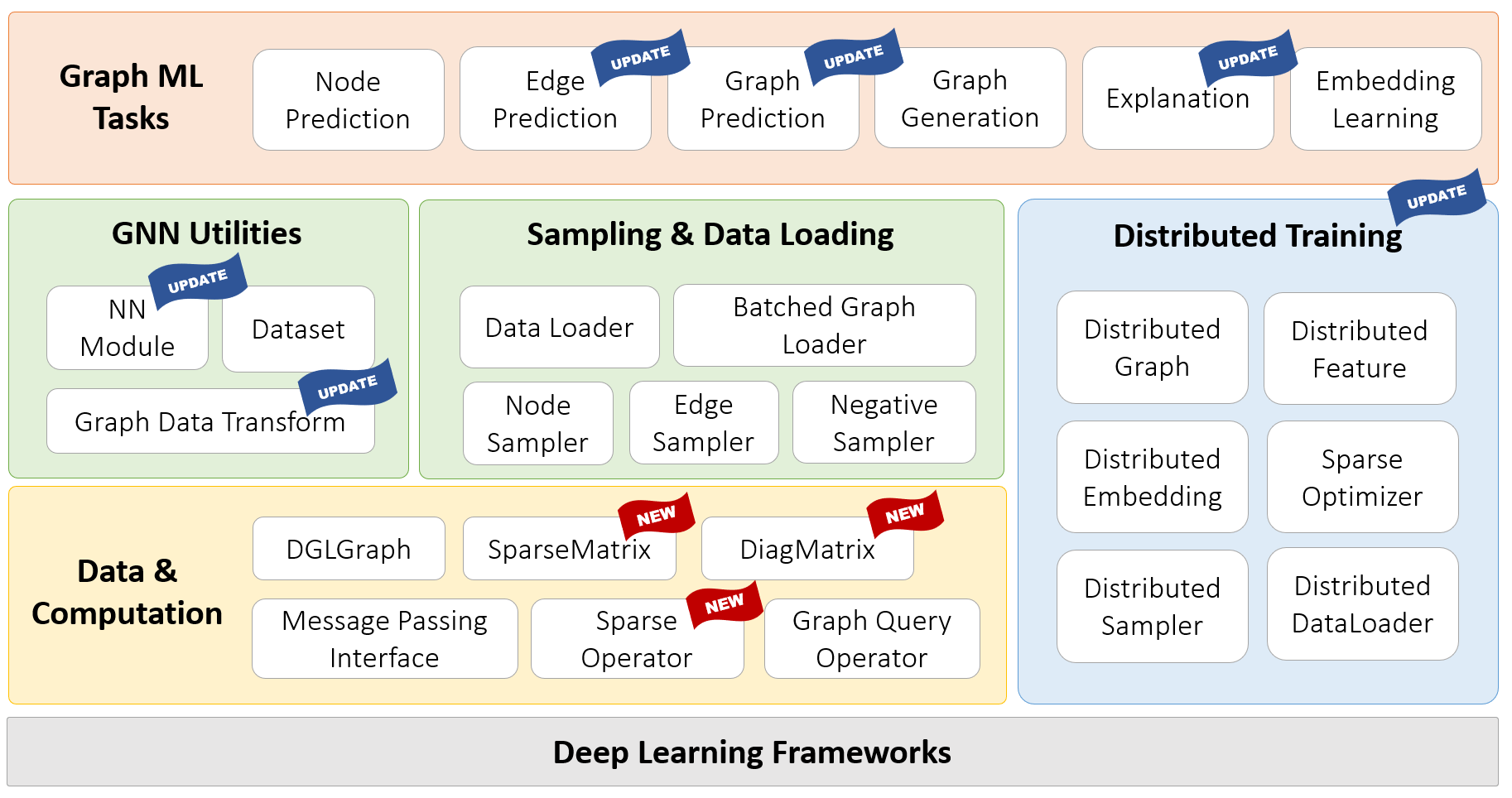
Deep Graph Library (DGL)

DGL 1.0 release

dgl blog [link]

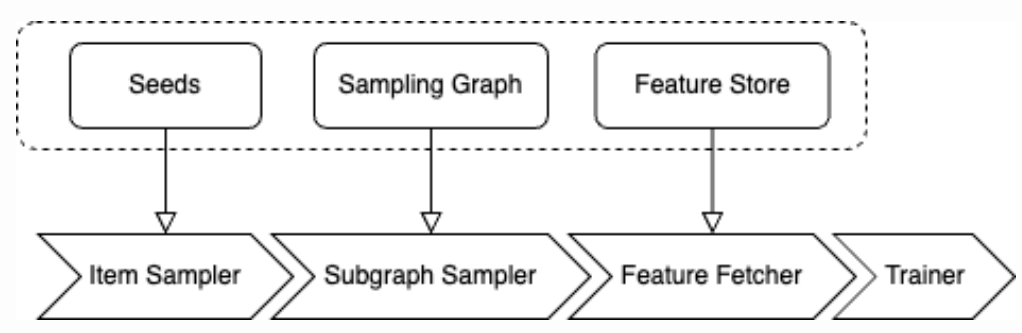
DGL 2.0 release

dgl blog [link]

Useful APIs and data structures

  • Named node and edge features
  • g.ndata['x']=X
  • g.edata['a']=E
  • Graph processing
  • dgl.add_reverse_edges(g)
  • dgl.add_self_loop(g)
  • Graph querying
  • g.num_nodes()
  • g.num_edges()
  • g.has_edges_between(u,v)
  • g.in_degrees()

 

  • \( h_u=\frac{1}{N_u}\sum_{V \in N_u}x_v \) =  g.update_all(fn.copy_u('x', 'm'), fn.mean('m','h'))
  • Message passing APIs
  • Increasingly supporting heterogeneous graphs

PyTorch Geometric (PyG)

 Built on top of PyTorch

  • Developed at TU Dortmund and Stanford Universities
  • Overlap with group that runs the Open Graph Benchmark
  • Standardizes the API around defining “message” and “update” functions, along with specifying an aggregator
  • Has a large set of built-in datasets and implementations

New(er) comers

  •  Jraph
  • Comes from DeepMind
  • Built on top of JAX
  •  TensorflowGNNs
  • Alpha release announced Nov 2021
  • Keras-style API
  • A stated emphasis on heterogeneous graphs

Open Graph Benchmark

  • Larger and more realistic benchmark graph datasets
  •  Node, Link and Graph property prediction tasks
  • Wrapped in a Python package for easy loading into PyGand DGL
  • Comes with a pre-defined train/val/test split
  • Also comes with built in “Evaluators” for each dataset to ensure performance is consistently measured
  • Each dataset has a leaderboard, each row is a method’s performance with paper + code
  • There’s also a “Large-Scale” version with much larger graphs

node classification colab

OGB [link]

  • Wang, M., Zheng, D., Ye, Z., Gan, Q., Li, M., Song, X., ... & Zhang, Z. (2019). Deep graph library: A graph-centric, highly-performant package for graph neural networks [pdf]

 

  • Fey, M., & Lenssen, J. E. (2019). Fast Graph Representation Learning with PyTorch Geometric Computer software [link]

 

  • Godwin*, J., Keck*, T., Battaglia, P., Bapst, V., Kipf, T., Li, Y., Sanchez-Gonzalez, A. (2020). Jraph: A library for graph neural networks in jax(Version 0.0.1.dev). Opgehaalvan [link]

 

  • Hu, W., Fey, M., Zitnik, M., Dong, Y., Ren, H., Liu, B., ... & Leskovec, J. (2020). Open graph benchmark: Datasets for machine learning on graphs [pdf]

Extra - Improving Scalability

The problem(s)

  • Many real-world/industrial graphs are billions of nodes and edges, perhaps 100s of billions
  • E.g., E-commerce products, reviews, transactions, sign-in events
  • You may not even be able to fit this into memory
  • In small-world graphs like social networks, ~6 GNN layers means every node in the graph is needed to calculate each node embedding

Sampling

  • Idea: maybe you don’t need the full graph to compute useful embeddings
  • In fact, having this source of randomness may make your model generalize better to new, slightly different neighborhoods
  • Can sample at different levels:
  • Subset of neighbors of each node during message passing
  • A set of nodes for each GNN layer
  • A subset of the graph for the full GNN

Node-level Sampling

  • Random neighbor sampling: for each node, only choose a subset of neighbors for message passing (e.g., GraphSAGE)
  • Still suffers from exponential growth with layers, but controllable
  • Importance sampling: try to improve the variance of your estimate by smarter sampling
  •  FastGCN and LADIES use importance sampling at the layer-level to reduce exponential growth to linear growth.

W. L. Hamilton, R. Ying, J. Leskovec: Inductive Representation Learning on Large Graphs [link]

J. Chen, T. Ma, C. Xiao: FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling [link]

D. Zou, Z. Hu, Y. Wang, S. Jiang, Y. Sun, Q. Gu: Layer-Dependent Importance Sampling for Training Deep and Large Graph Convolutional Networks [link]

Subgraph sampling

  • Cluster-GCN: Find densely connected clusters and only sample neighbors in the same cluster
  • GraphSAINT: Create random subgraphs for each minibatch and model with a GCN as if it were the full graph

W. Chiang, X. Liu, S. Si, Y. Li, S. Bengio, C. Hsieh: Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks [link]

H. Zeng, H. Zhou, A. Srivastava, R. Kannan, V. Prasanna: GraphSAINT: Graph Sampling Based Inductive Learning Method [link]:

Pre-computation

  • Idea: instead of doing message passing before each MLP layer, do graph-based processing once
  • Assumes that the non-linearity between GNN layers is not important, so the model fitting phase is ~ logistic regression
  • Can be done in one big batch-processing job, not during training process
  • Simple Graph Convolution (SGC): \( H = softmax(A^KX\theta) \)
  • Scalable Inception Graph Neural Networks (SIGN): Similar to SGC, but also consider general operators, not just powers of A (e.g., counting triangles, diffusion operators like Personalized Page Rank,..., etc) and concatenate results as features

M. Chen, Z. Wei, Z. Huang, B. Ding, Y. Li: Simple and Deep Graph Convolutional Networks [link]

F. Frasca, E. Rossi, D. Eynard, B. Chamberlain, M. Bronstein, F. Monti: SIGN: Scalable Inception Graph Neural Networks [link]

H. Wang, Z. Wei, J. Gan, S. Wang, Z. Huang: Personalized PageRank to a Target Node, Revisited [pdf]

Resource management

  • There are optimizations that can be made to improve resource utilization
  • GNNAutoScale caches historical embeddings from previous minibatches to avoid re-computing them
  • ROC and DistGNN enable fast/scalable distributed training via memory and graph partitioning optimizations

M. Fey, Jan E. Lenssen, F. Weichert, J. Leskovec: GNNAutoScale: Scalable and Expressive Graph Neural Networks via Historical Embeddings [link]

Z. Jia, S. Lin, M. Gao, M. Zaharia, A. Aiken: Improving the accuracy? scalability, and perfomance of graph neural networks with ROC [pdf]

V. Md, S. Misra, G. Ma, R. Mohanty, E. Georganas, A. Heinecke, D. Kalamkar, N. K. Ahmed, S. Avancha: DistGNN: Scalable Distributed Training for Large-Scale Graph Neural Networks [link]

Deep Graph Library (DGL)

By karpovilia

Made with Slides.com

Deep Graph Library (DGL)

  • 236

More from karpovilia