FLoC 2018
Selected Talks
Dependency Quantified Boolean Formulas
| QBF |
|
PSPACE-complete |
| DQBF | Dependencies explicitly specified | NEXPTIME-complete |
Every \(\exists\) depends on all \(\forall\) before it.
Dependency Quantified Boolean Formulas
\(\forall x_1...\forall x_n \exists y_1(D_{y1}).. y_n(D_{yn}) : \phi \)
with \(D_{yi} \subseteq \{x_i, ..., x_n\}\)
General Form:
Dependency Quantified Boolean Formulas
Example:
\(\forall x_1, x_2, x_3 \exists y_1 (x_1,x_2), y_2(x_1,x_3):\phi\)
\(\forall x_1\)
\(\forall x_2\)
\(\forall x_3\)
\(\exists y_1\)
\(\exists y_2\)
\(S_{y_1}(t,t)\)
\(S_{y_1}(t,t)\)
\(S_{y_1}(t,f)\)
\(S_{y_1}(t,f)\)
\(S_{y_2}(t,t)\)
\(S_{y_2}(t,f)\)
\(S_{y_2}(t,t)\)
\(S_{y_2}(t,f)\)
Dependency Quantified Boolean Formulas
Example:
\(\forall x_1, x_2, x_3 \exists y_1 (x_1,x_2), y_2(x_1,x_3):\phi\)
\(\forall x_1\)
\(\forall x_2\)
\(\forall x_3\)
\(\exists y_1\)
\(\exists y_2\)
Dependency Quantified Boolean Formulas
Example application: Partial Equivalence Checking
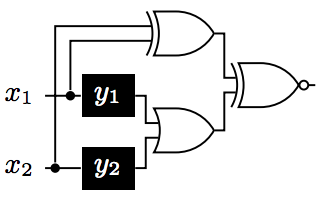
\(\forall x_1 x_2 \exists y_1 y_2\) \(\forall x_1 \exists y_1 \forall x_2 \exists y_2\) \(\forall x_1 \exists y_2 \forall x_2 \exists y_1\)
Linearizations cannot express the problem
Rabe: "DQBF can encode existential quantification over functions"
Dependency Quantified Boolean Formulas
Solved using:
- Incomplete Approximations: implicit depencies \(\supseteq\) explicit
- Search + Skolem clauses
- Universal Expansion
- until QBF: Eliminate \(x_i\) from incomparable dependency sets (MAXSAT)
- until SAT: (potentially) exponential increase of variables
- (information fork resolution)
Dependency Quantified Boolean Formulas
More expressive/harder problems
Can model \[\forall x : (\forall y : \phi(x,y)) \land (\forall z : \psi(x,z))\]
without loss of information/smaller search space
Approximation Fixpoint Theory and the Well-Founded Semantics of Higher-Order Logic Programs
See original slides
PySAT: A Python Toolkit for
Prototyping with SAT Oracles
- Python toolkit for working with multiple SAT solvers
- Its MAXSAT implementation won the MAXSAT competition
FLoC 2018
By krr
FLoC 2018
- 1,535


