Functionals and Bases

Outline

  • Functionals of exchange and correlation (Ch 5,8)

  • Pseudopotentials (Ch 10,11)

  • Choosing basis (Ch 12-15)

  • KKR approach (Ch 16.3)

Recap

Many-body problem

\hat{H}=\sum\limits_{i=1}^{N_e}\frac{-\hbar^2\nabla_i^2}{2m}+ \sum\limits_{I=1}^{N_n}\frac{-\hbar^2\nabla_I^2}{2M_I}+\sum\limits_{i,I}V_{en}(\mathbf{r}_i-\mathbf{R}_I)\\ +\frac{1}{2}\sum\limits_{i,j}V_{ee}(\mathbf{r}_i-\mathbf{r}_j)+\frac{1}{2}\sum\limits_{I,J}V_{nn}(\mathbf{R}_I-\mathbf{R}_J)

no generic exact solution

Kohn-Sham equations

Minimizing the constrained energy functional:

\displaystyle \frac{-\hbar^2\nabla^2}{2m}\varphi_i(\mathbf{r})+ \underbrace{\left(v_\text{ext}(\mathbf{r})+\int\frac{n(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\text{d}\mathbf{r}'+\frac{\delta E_{xc}[n]}{\delta n}\right)}_{v_{eff}(\mathbf{r})}\varphi_i(\mathbf{r}) =\epsilon_i\varphi_i(\mathbf{r})

Exchange-correlation potential:

\displaystyle v_{xc}(\mathbf{r})=\frac{\delta E_{xc}[n(\mathbf{r})]}{\delta n(\mathbf{r})}

HK theorems tell us that we can progress based just on the density \(n(\mathbf{r})\) !

What does and does not exact DFT do ?

  • Are excitation energies given correctly by the exact density functional theory?
    Yes. In principle, all properties are determined since the entire Hamiltonian is determined.
  • Are excitation energies given correctly by minimization of the exact Hohenberg–Kohn functional?
    No. The functional evaluated near the minimum provides no information about excitations, which are associated with saddle points at higher energies.
  • Are static susceptibilities given correctly by the ground state functional?
    Yes. All static susceptibilities are second derivatives of ground state energies with respect to external fields.
  • Is the exact Fermi surface of a metal given by the exact ground state density functional theory?
    Yes. This is not a trivial question for two reasons. First, for the question to be meaningful, the many-body metal must have a well-defined Fermi surface; for the present purposes, we assume this. Second, it is not a priori obvious that the Fermi surface is a ground state property.
  • Must a Mott insulator (an insulator due to correlations among the electrons) be predicted correctly by the exact density functional theory?
    Yes. This follows from the above arguments on a metal in the special case where the Fermi surface vanishes.

How can we get \(E_{xc}\) ?

 

  • We guess?!?

     
  • We assume density is locally smooth and build on the homogeneous electron gas!

     
  • Benchmark against experiments!

     
  • Try to keep parameters at bay.

Homogeneous electron gas

E_{xc}=E_x+E_c
E_x=-\frac{3}{4}\left (\frac{6}{\pi} n \right )^\frac{1}{3}=-\frac{3}{4\pi}\left (\frac{9\pi}{4} \right )^\frac{1}{3}/r_s
E_c=?

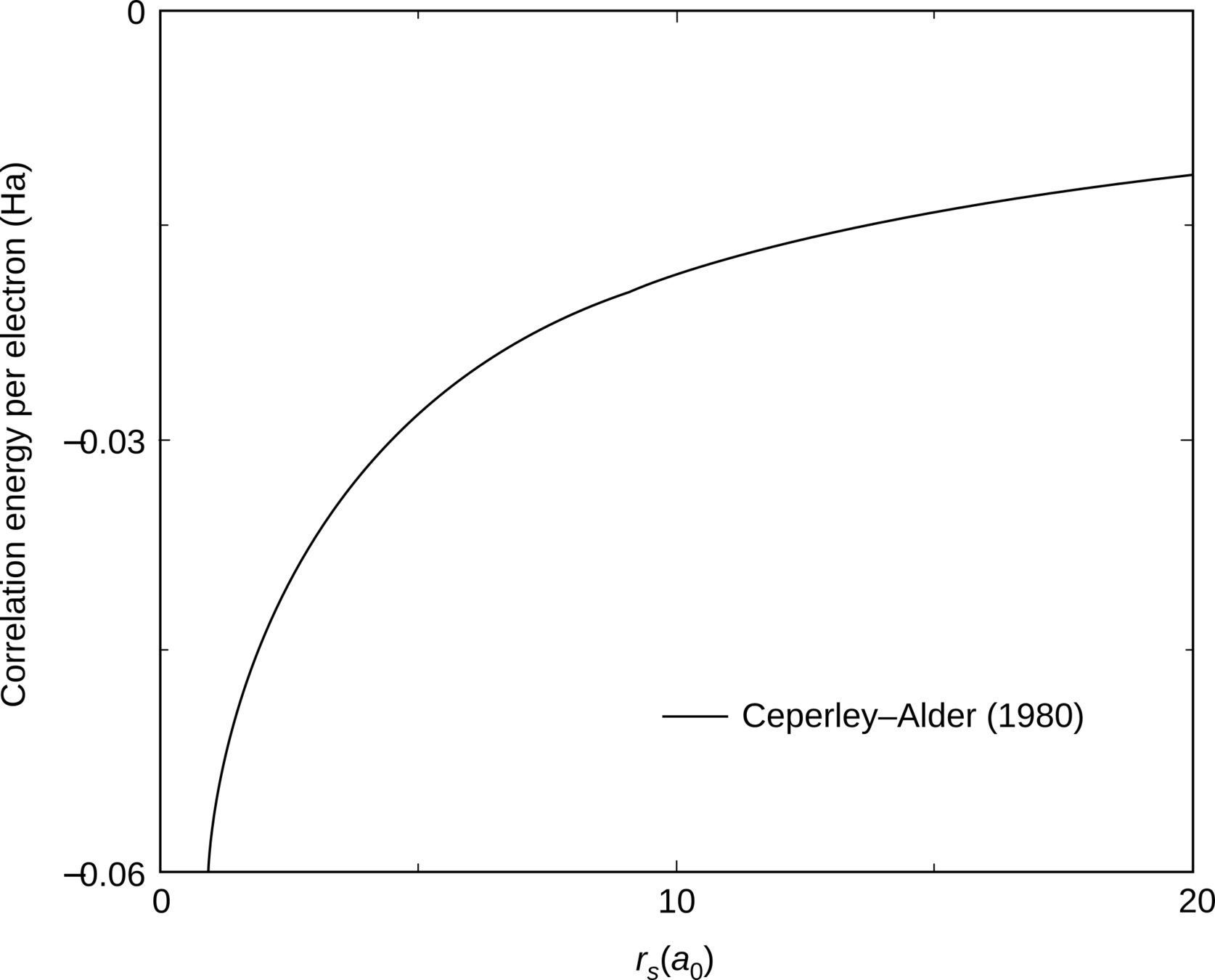
use an exact numerical method:

QMC

Ceperley and Alder Phys. Rev. Lett. 45, 566 (1980)

Interpolation formulas for \(E_{c}\) 

Perdew and Zunger; Phys. Rev. B 23, 5048  (1981)
Vosko, Wilkes, and Nussair; Can. J. Phys. 58, 1200 (1980)

Functionals of exchange and correlation

  • S: The Slater exchange, ρ4/3 with theoretical coefficient of 2/3, also referred to as Local Spin Density exchange [Hohenberg64, Kohn65, Slater74]. Keyword if used alone: HFS.
  • XA: The XAlpha exchange, ρ4/3 with the empirical coefficient of 0.7, usually employed as a standalone exchange functional, without a correlation functional [Hohenberg64, Kohn65, Slater74]. Keyword if used alone: XAlpha.
  • B: Becke’s 1988 functional, which includes the Slater exchange along with corrections involving the gradient of the density [Becke88b]. Keyword if used alone: HFB.
  • PW91: The exchange component of Perdew and Wang’s 1991 functional [Perdew91, Perdew92, Perdew93a, Perdew96, Burke98].
  • mPW: The Perdew-Wang 1991 exchange functional as modified by Adamo and Barone [Adamo98].
  • G96: The 1996 exchange functional of Gill [Gill96, Adamo98a].
  • PBE: The 1996 functional of Perdew, Burke and Ernzerhof [Perdew96a, Perdew97].
  • O: Handy’s OPTX modification of Becke’s exchange functional [Handy01, Hoe01].
  • TPSS: The exchange functional of Tao, Perdew, Staroverov, and Scuseria [Tao03].
  • RevTPSS: The revised TPSS exchange functional of Perdew et. al. [Perdew09, Perdew11].
  • BRx: The 1989 exchange functional of Becke [Becke89a].
  • PKZB: The exchange part of the Perdew, Kurth, Zupan and Blaha functional [Perdew99].
  • wPBEh: The exchange part of screened Coulomb potential-based final of Heyd, Scuseria and Ernzerhof (also known as HSE) [Heyd03, Izmaylov06, Henderson09].
  • PBEh: 1998 revision of PBE [Ernzerhof98].
  • VWN: Vosko, Wilk, and Nusair 1980 correlation functional(III) fitting the RPA solution to the uniform electron gas, often referred to as Local Spin Density (LSD) correlation [Vosko80] (functional III in this article).
  • VWN5: Functional V from reference [Vosko80] which fits the Ceperly-Alder solution to the uniform electron gas (this is the functional recommended in [Vosko80]).
  • LYP: The correlation functional of Lee, Yang, and Parr, which includes both local and non-local terms [Lee88, Miehlich89].
  • PL (Perdew Local): The local (non-gradient corrected) functional of Perdew (1981) [Perdew81].
  • P86 (Perdew 86): The gradient corrections of Perdew, along with his 1981 local correlation functional [Perdew86].
  • PW91 (Perdew/Wang 91): Perdew and Wang’s 1991 gradient-corrected correlation functional [Perdew91, Perdew92, Perdew93a, Perdew96, Burke98].
  • B95 (Becke 95): Becke’s τ-dependent gradient-corrected correlation functional (defined as part of his one parameter hybrid functional [Becke96]).
  • PBE: The 1996 gradient-corrected correlation functional of Perdew, Burke and Ernzerhof [Perdew96a, Perdew97].
  • TPSS: The τ-dependent gradient-corrected functional of Tao, Perdew, Staroverov, and Scuseria [Tao03].
  • RevTPSS: The revised TPSS correlation functional of Perdew et. al. [Perdew09, Perdew11].
  • KCIS: The Krieger-Chen-Iafrate-Savin correlation functional [Rey98, Krieger99, Krieger01, Toulouse02].
  • BRC: Becke-Roussel correlation functional [Becke89a].
  • PKZB: The correlation part of the Perdew, Kurth, Zupan and Blaha functional [Perdew99].
  • VP86: VWN5 local and P86 non-local correlation functional.
  • V5LYP: VWN5 local and LYP non-local correlation functional.
  • VSXC: van Voorhis and Scuseria’s τ-dependent gradient-corrected correlation functional [VanVoorhis98].
  • HCTH/*: Handy’s family of functionals including gradient-corrected correlation [Hamprecht98, Boese00, Boese01]. HCTH refers to HCTH/407, HCTH93 to HCTH/93, HCTH147 to HCTH/147, and HCTH407 to HCTH/407. Note that the related HCTH/120 functional is not implemented.
  • tHCTH: The τ-dependent member of the HCTH family [Boese02]. See also tHCTHhyb below.
  • B97D: Grimme’s functional including dispersion [Grimme06]. B97D3 requests the same but with Grimme’s D3BJ dispersion [Grimme11].
  • M06L [Zhao06a], SOGGA11 [Peverati11], M11L [Peverati12], MN12L [Peverati12c] N12 [Peverati12b] and MN15L [Yu16a] request these pure functionals from the Truhlar group.

Non-empirical Functionals 

\displaystyle E^{LDA}_{xc}[n]=\int \epsilon_{LDA}(n)n(r) \mathrm{d}r
\displaystyle E^{GGA}_{xc}[n]=\int \epsilon_{GGA}(n,|\nabla n|)n(r) \mathrm{d}r
\displaystyle E^{LSDA}_{xc}[n_\uparrow,n_\downarrow]=\int \epsilon_{LSDA}(n_\uparrow,n_\downarrow)n(r) \mathrm{d}r

No fitting to experiments, based only on general rules of quantum mechanics!

Hybrid functionals

A mixture of the exactly calculable HF exchange and other \(E_{xc}\) parametrizations

E^{HF}_{x}=-\frac{1}{2}\displaystyle\sum_{ij}\int \mathrm{d}\mathbf{r}_1\mathrm{d}\mathbf{r}_2 \frac{\psi^*_i(\mathbf{r}_1)\psi^*_j(\mathbf{r}_2)\psi_i(\mathbf{r}_2)\psi_j(\mathbf{r}_1)}{r_{12}}
\begin{aligned} B^{B3LYP}_{xc}&=E^{LDA}_x+a_0(E^{HF}_x-E^{LDA}_x)\\ &+a_x(E^{GGA}_x-E^{LDA}_x)\\ &+E^{LDA}_c+a_c(E^{GGA}_c-E^{LDA}_c)\\ a_0&=0.20,\, a_x=0.72,\,a_c=0.81 \end{aligned}

A. D. Becke, J. Chem. Phys. 98, 5648 (1993)

Addresses some of the spectral problems of LDA and GGA.

The prefered choice among chemists.

Fitted to experimental data!!

Which functional should I choose?

  • At any given time, and for any given property and system, there is at most a “best” answer.                                                                                
  • Experience and benchmarking are always needed to find that best answer.

Rappoport et al.   Encyclopedia of Inorganic Chemistry  (2009)

Properties obeyed by “exact Kohn–Sham theory”

  • Are static charge and spin susceptibilities given correctly by the ground state functional?
    Yes. All static susceptibilities are second derivatives of ground state energies with respect to external fields. Thus they must be given correctly by the variation of the ground state Kohn–Sham functional as functions of external fields. 
  • Is the macroscopic polarization in a crystal given correctly by the Kohn–Sham theory in terms of the density n(r) in the bulk of the crystal?
    No. It has long been known that the polarization could not be derived simply from the density. Recent developments derive the polarization from the phases of the wavefunctions not given correctly by the Kohn–Sham orbitals.
  • Is the exact Fermi surface of a metal given by eigenvalues in the exact Kohn–Sham theory?
    No. Even though the density is reproduced, the Fermi surface may not be correct due to the requirement of a local potential.
  • Must a Mott insulator – an insulator due to correlations among the electrons – be predicted correctly by the eigenvalues in the exact Kohn–Sham theory?
    No. This follows from the above arguments on a metal that the Fermi surface is not correct in general.
  • Are excitation energies given correctly by the eigenvalues of the Kohn–Sham equations?
    No. The eigenvalues are not the true energies for adding or subtracting electrons, nor for neutral excitations.
  • Is any excitation energy given correctly by an eigenvalue of the Kohn–Sham equations?
    Yes. The highest eigenvalue in a finite system must be correct [354] since that state dominates the long-range tail of the density, which is defined to be correct.
  •  Is it possible to determine excitation energies by any means using the Kohn–Sham theory?
    Yes. This question is in the spirit of the Hohenberg–Kohn existence proofs. Since the Kohn–Sham density is exact by construction, it follows from the Hohenberg–Kohn theorems that all properties are determined since the entire Hamiltonian is determined. 

Pseudopotentials

Motivation:

  • Reduction of basis set size
  • Reduction of number of electrons

Approximations:

  • One-electron picture
  • Core electrons are not overlapping with the rest (small core approx)

 

Potential is not local, each angular momentum channel feels different potential:

V_{ps}(\mathbf{r})=\displaystyle\sum_{lm} \left | lm \right \rangle V_{lm}(\mathbf{r}) \left \langle lm \right |

Norm conserving Pseudopotentials

  1. Inside a cut-off radius  \(r_c\), the norm of each pseudo-wavefunction be identical to its corresponding all-electron wavefunction:$${\displaystyle \int _{r<r_{c}}dr^{3}\phi _{\mathbf {R} ,i}({\vec {r}})\phi _{\mathbf {R} ,j}({\vec {r}})=\int _{r<r_{c}}dr^{3}{\tilde {\phi }}_{\mathbf {R} ,i}({\vec {r}}){\tilde {\phi }}_{\mathbf {R} ,j}({\vec {r}})} $$where \( \phi _{\mathbf {R} ,i}\) and \(\tilde {\phi }_{\mathbf {R} ,i}\) are the all-electron and pseudo reference states for the pseudopotential on atom  positioned at \(\mathbf{R}\).                            
  2. All-electron and pseudo wavefunctions are identical outside cut-off radius  \(r_c\) .

 

Ultrasoft Pseudopotentials

\( |p_{\mathbf {R} ,i}\rangle \)​ are duals of ​\(|\tilde{\phi }_{\mathbf{R},j}\rangle \) inside the cutoff 

$$ {\displaystyle \langle p_{\mathbf {R} ,i}|{\tilde {\phi }}_{\mathbf {R} ,j}\rangle _{r<r_{c}}=\delta _{i,j}}$$

Vanderbilt,  Phys. Rev. B 41, 7892 (1990).

  • Norm is not conserved
  • General eigenvalue problem is needed                                                                             
  • The necessary basis is reduced

$$ {\displaystyle q_{\mathbf {R} ,ij}=\langle \phi _{\mathbf {R} ,i}|\phi _{\mathbf {R} ,j}\rangle -\langle {\tilde {\phi }}_{\mathbf {R} ,i}|{\tilde {\phi }}_{\mathbf {R} ,j}\rangle }, $$

$${\displaystyle {\hat {H}}|\Psi _{i}\rangle =\epsilon _{i}{\hat {S}}|\Psi _{i}\rangle }$$

$$ {\displaystyle {\hat {S}}=1+\sum _{\mathbf {R} ,i,j}|p_{\mathbf {R} ,i}\rangle q_{\mathbf {R} ,ij}\langle p_{\mathbf {R} ,j}|}, $$

Transferability

\(r_c\)=?

Softness:

  • number of basis functions needed for converged results

Transferability:

  • same pesudopotential should be good in atoms, molecules and in solids, independent from chemical environment

Large \(r_c\) makes more soft potentials, but throwing out a large chunk of the core  we loose physics 

Transferability

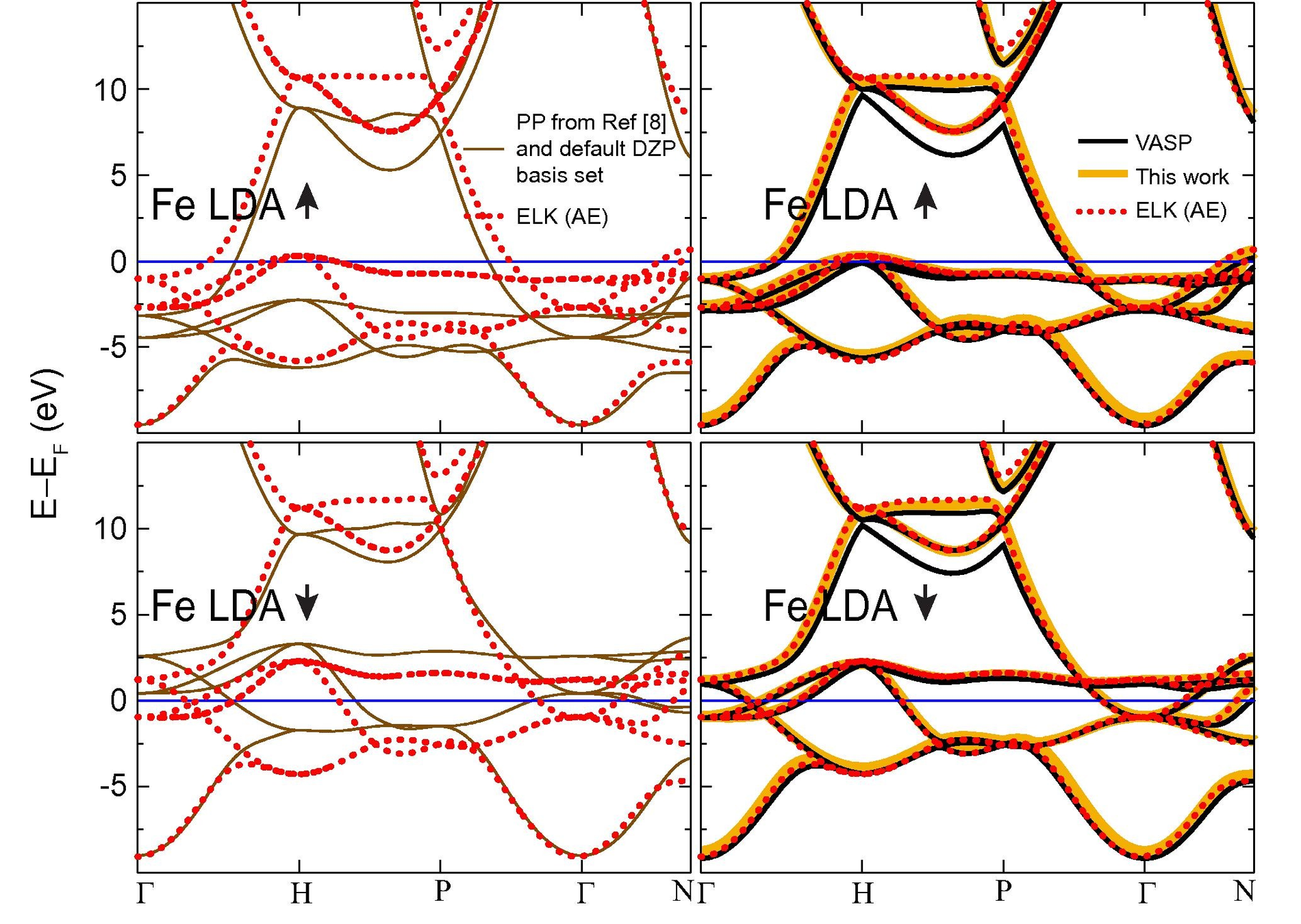
Comp. Mat. Sci. 98, 372 (2015)

The choice of basis

\displaystyle\phi_i(r)=\sum_pa_{ip}\chi_p(r)
PRO CON
Plane waves
 		 -simple to implement
-one convergence parameter		 - resource hungry
- big basis set needed
Atomic like orbitals - small basis
- sparse matrix methods
- scales to BIG systems		 -harder to implement
-many things influence
 convergence
KKR method
baseless method..
relies on scattering approach and Green's functons		 -relativistic effects are easy
-standard for magnetic systems
-most accurate for some  problems		 -harder to implement
-smaller community
-some features not yet  implemented..
\chi_p(\mathbf{r})=\mathrm{e}^{\mathrm{i}\mathbf{p}\cdot\mathbf{r}}
\chi_{nlm}(r)=R_{nl}(\rho)Y_{l}^m(\hat{r})

Plane Wave basis

\chi_p(r)=\mathrm{e}^{\mathrm{i}pr}

Single convergence parameter:

size of basis, #\(p\),  usually BIG

  • atomic potentials are sharp features
  • we need a lot of Fourier components
  • Pseudopotentials help but still a large basis is needed
  • Kinetic term computed via FFT

Projector Augmented  Wave basis

  • Mapping all electron problem to a problem where the core is smooth.

     
  • Augmentation regions around each nucleus are introduced and integrals within each sphere are done in spherical coordinates.       

     
  • Localized functions keep all the information on the core states.

     
  • Similar in mathematical formulation to ultrasoft pseudopotentials.

P. E. Blöchl Phys. Rev. B 50, 17953 (1994)

Numeric Atomic like orbitals

  • Very efficient
  • Less straight forward variational convergence
  • Freedom : RADIAL SHAPE
  • Numerical solution of the Kohn-Sham Hamiltonian for the isolated pseudoatom with the same approximations (xc, pseudos) as for the system

Numeric Atomic like orbitals

\left (-\frac{1}{2r}\frac{\partial^2}{\partial r}r+\frac{l(l+1)}{2r^2}+V_l(r) \right)\phi_l(r)=(\epsilon_l+\delta \epsilon_l) \phi_l(r)

energy shift

single-\(\zeta\)

Energy shift enforces a node in the wavefunction! It is cut after the node!

double-\(\zeta\):

more radial freedom

\phi_{l}^{2\zeta}(r)=\begin{cases} r^{l}(a_{l}-b_{l}r^{2}) & r\le r_{l}^{s}\\ \phi_{l}^{1\zeta}(r) & r\ge r_{l}^{s} \end{cases}

split orbital at radius \(r^s_l\)

polarization:

more angular freedom

  • derived from a perturbation due to a homogeneous electric field
  • wave function with angular momentum \(l+1\)

Numeric atomic orbital

vs

plane wave

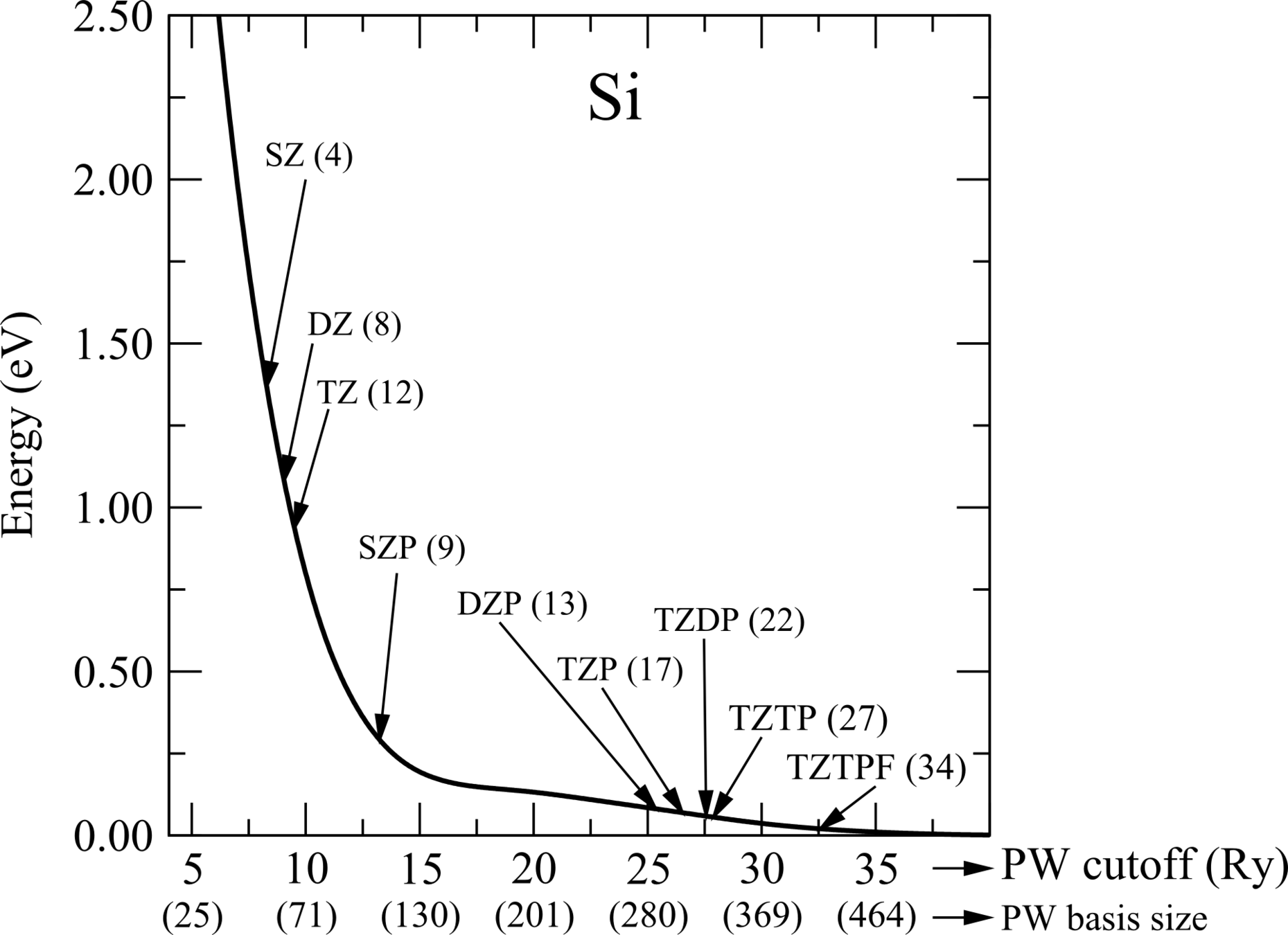
J. Phys.: Condens. Matt. 14, 2745 (2002).

KKR approach

Instead of Schrödinger, we have Green!

 $$\displaystyle \left[{-{\frac {\hbar ^{2}}{2m}}{\nabla ^{2}}+V({\bf {r}})-E}\right]G(E,{\bf {r}},{\bf {r'}})=-\delta ({\bf {r}}-{\bf {r'}})$$

$$({G}^{-1}_0-{V}){G}={I}$$

We know \({G}_0\) analytically even in the case of fully relativistic (Dirac) physics! 

 $$\displaystyle \left[{-{\frac {\hbar ^{2}}{2m}}{\nabla ^{2}}+V({\bf {r}})}\right]\psi({\bf {r}})=E\psi({\bf {r}})$$

\(G=G_0+G_0VG_0+\dots\)

\(G=G_0+G_0TG\)

\(T=V+VG_0V\dots\)

\(T=V+VG_0T\)

 

\(T=(V^{-1}-G_0)^{-1} \)

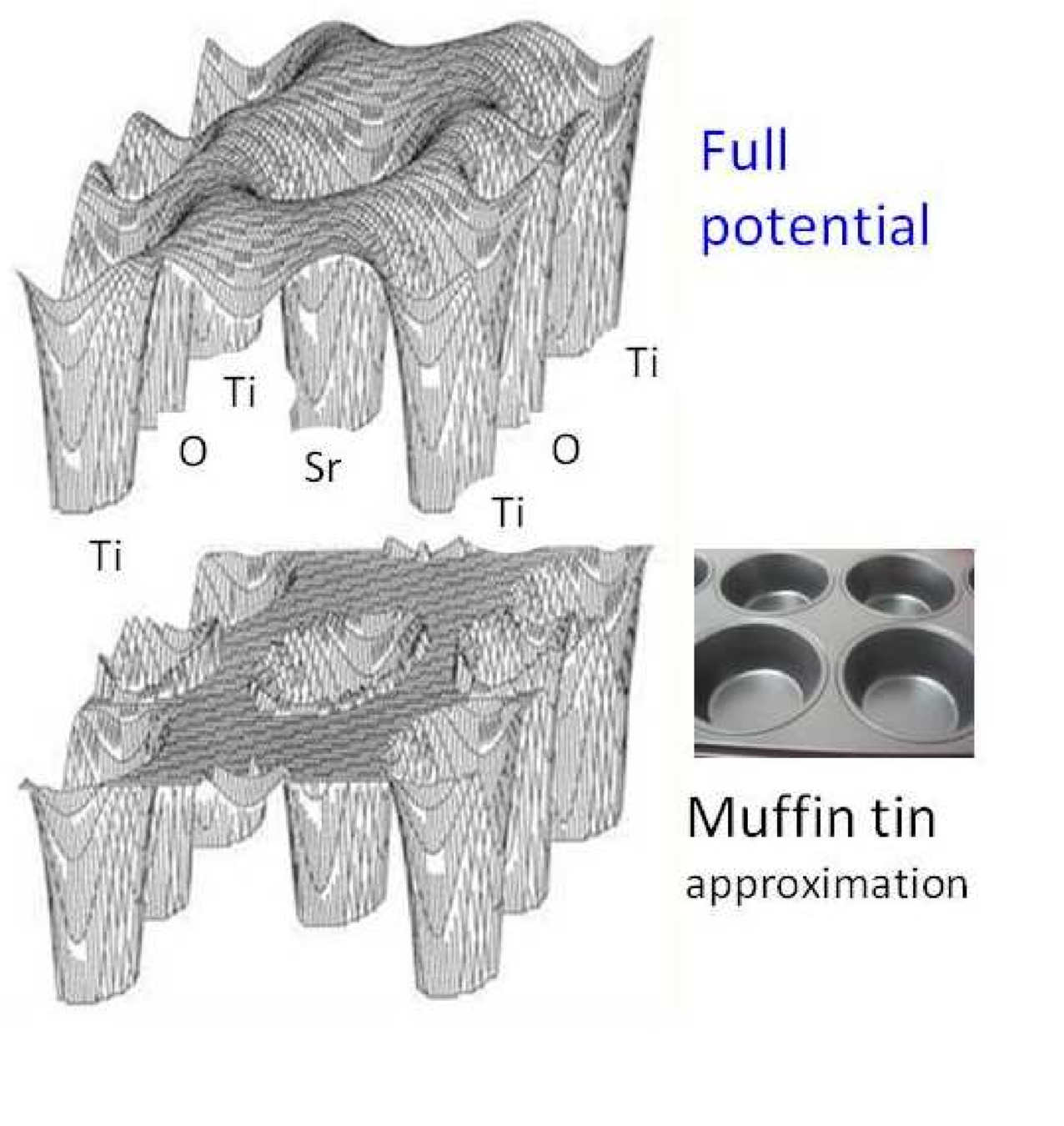
What is DFT good at?

  • structural properties



     
  • electronic structure of simple systems

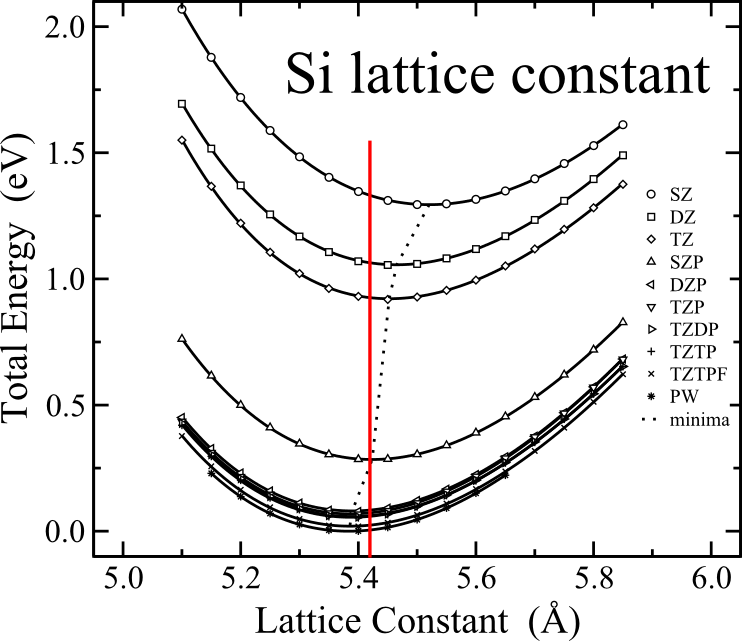
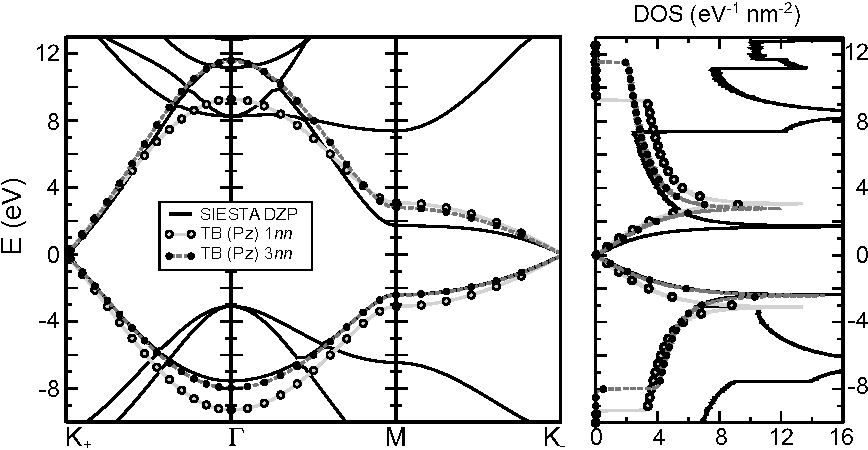
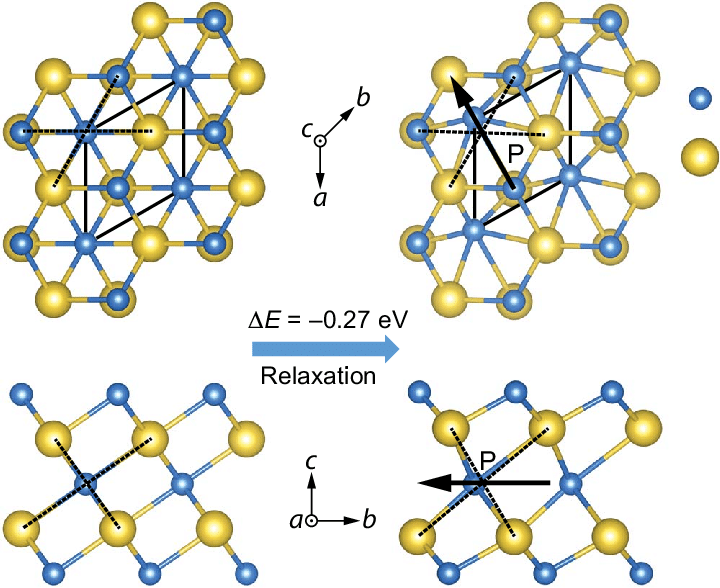
Failures of DFT

  • GAPs
     

 

 

 

  • Strong(ish) interactions

LDA+U:

J. Phys.: Cond. Matt. 9,767 (1997)

DMFT:

Phys. Rev. Lett. 62, 324 (1989)

QMC:

Rev. Mod. Phys. 73, 33 (2001)

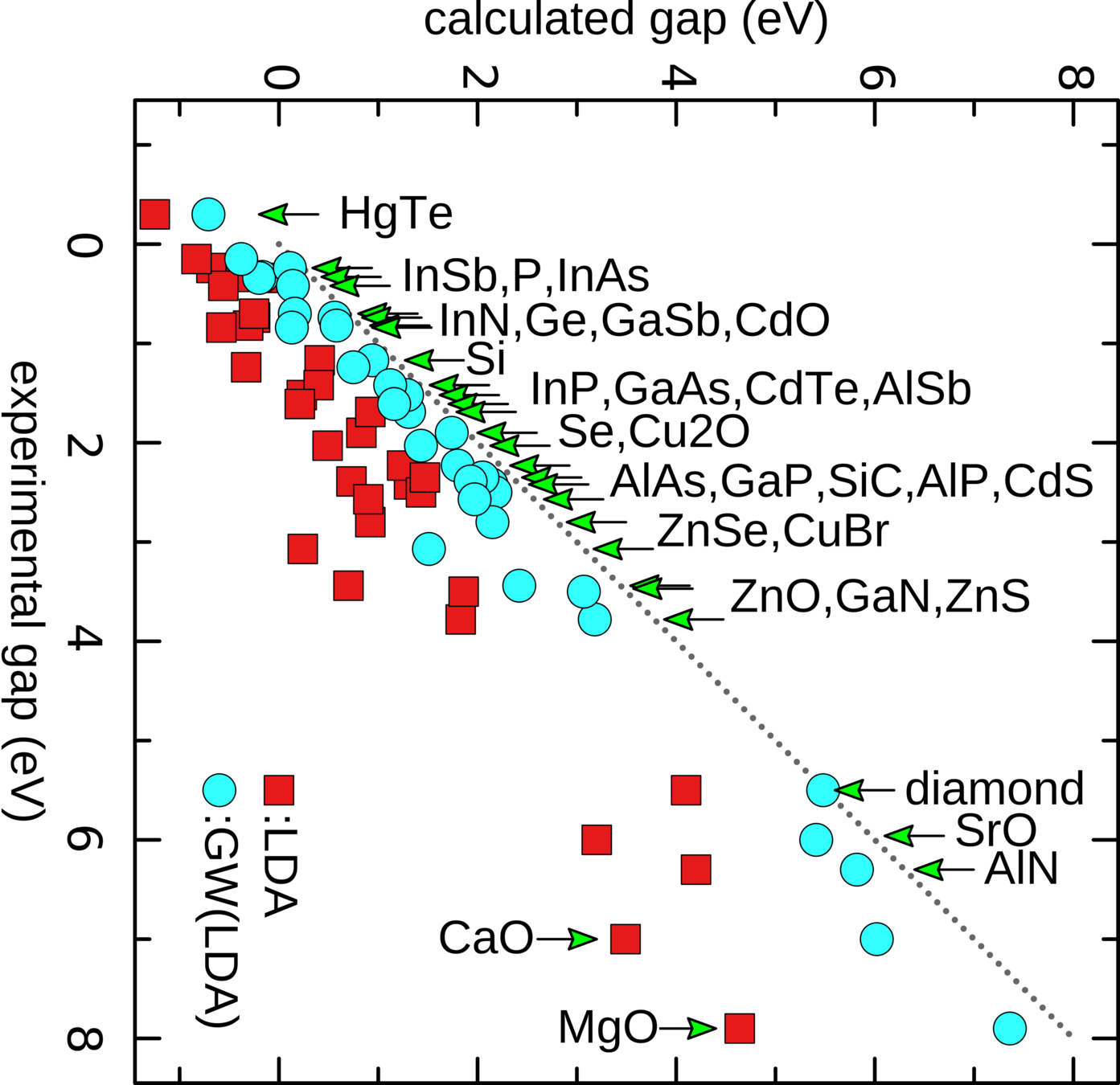
GW:

Phys. Rev. 139, A796 (1965)

BSE:

Phys. Rev. Lett. 75, 818 (1995)

State of the art-plane wave

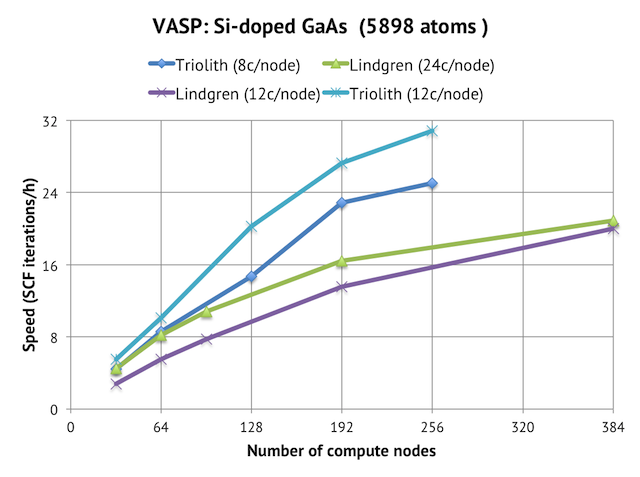
6000 atom

3000 proc

120s/scf

Massively  

parallel

Phonon spectrum

J. Chem. Phys. 143, 064710 (2015)

Excitations with

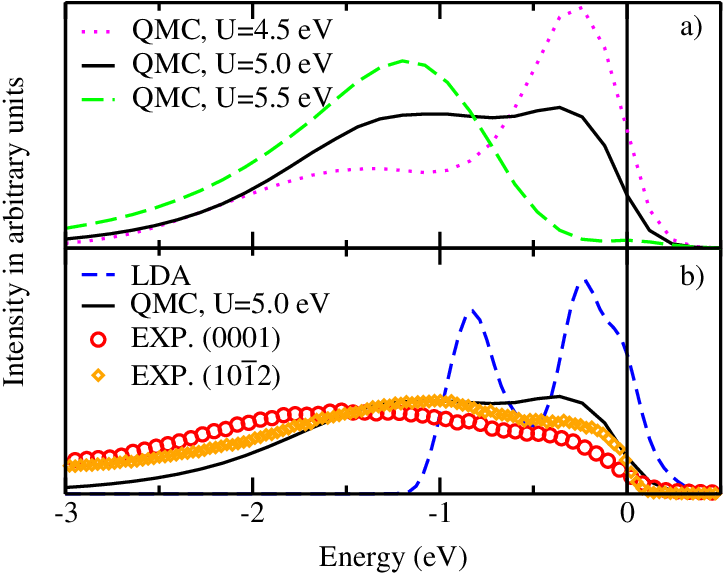
GW method

Phys. Rev. B 75, 235102 (2007)

State of the art-PAO

J. Phys.: Cond. Matt. 27, 054004 (2015)

J. Phys.: Cond. Matt. 26, 305503 (2014)

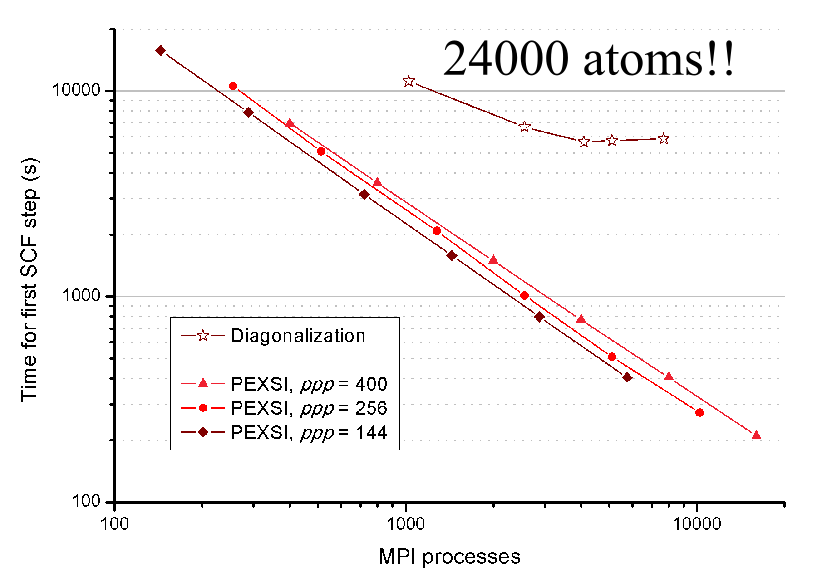
6000 atom

2000 proc

10 sec/scf

SIESTA-PEXSI parallelization

New J.  Phys., 16, 093029 (2014)

Phys. Rev. B 65, 165401 (2002)

Local quantities (e.g. STM)

Ideal as an input for transport calculations

https://launchpad.net/siesta

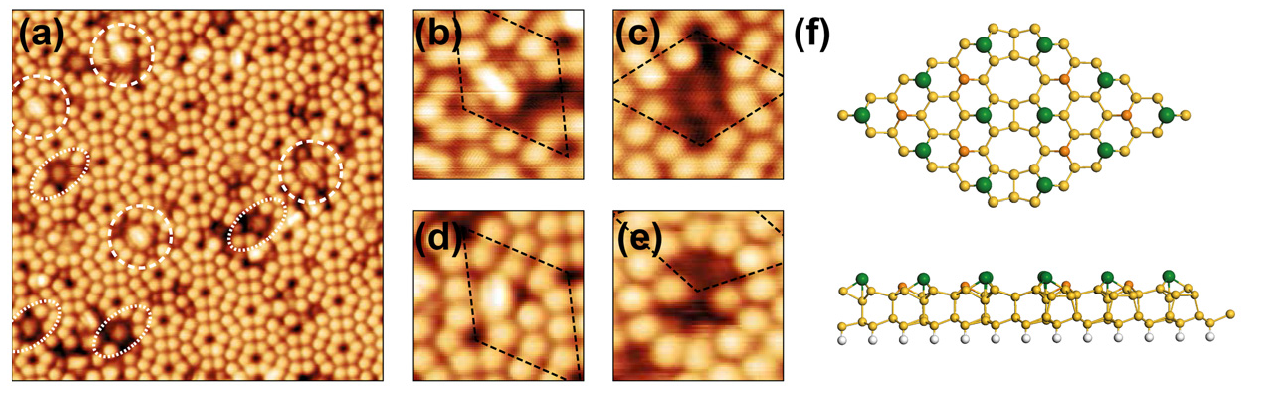
State of the art-KKR

KKRNano @ http://www.judft.de/   massive parallelization

PRB 94, 104511 (2016)

abinitio superconductivity

PRB 89, 224401 (2014)

finite temperature magnetism

PRB 82, 024411 (2010)

ARPES+DMFT

Budapest

München

Jülich

Functionals and Bases

By László Oroszlány

Functionals and Bases

  • 823

More from László Oroszlány