Nodal line semimetals
László Oroszlány ELTE-KRFT
Outline
-
Topology in real and momentum space
-
Topological metals
-
Magnetic oscillations of nodal loop semimetals
Topology
in
real space
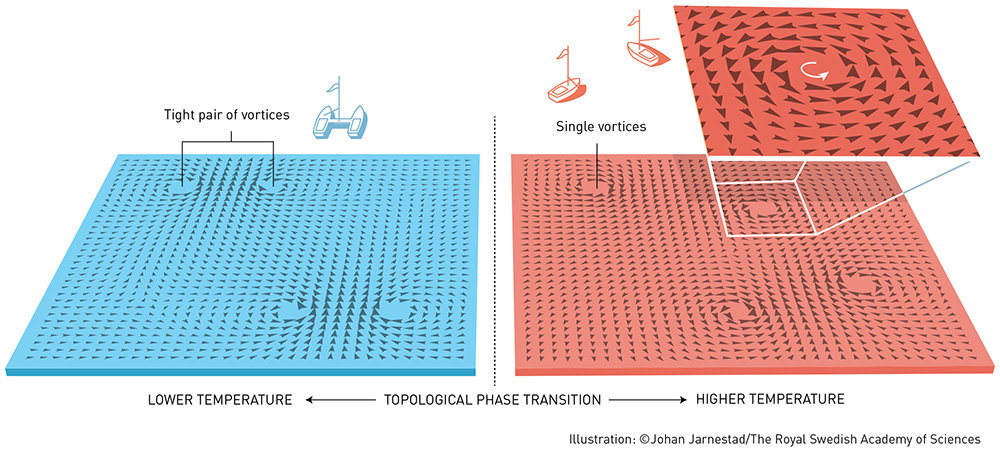
Berezinskii–Kosterlitz–Thouless transition
Berezinskii, Sov. Phys. JETP, 32 493 (1971)
Kosterlitz, Thouless, J. Phys. C, 6 1181 (1973)
2D XY model has a phase transition despite the
Mermin-Wagner theorem!
Skyrmions in magnetic systems
Phys. Rev. Lett. 87, 037203 (2001)
\vec{r}=
\left(\begin{array}{c}
r_x\\
r_y
\end{array}\right)
\vec{d}(\vec{r})=
\left(\begin{array}{c}
d_x(\vec{r})\\
d_y(\vec{r})\\
d_z(\vec{r})
\end{array}\right)
\displaystyle
C=\frac{1}{4\pi}\int \vec{d}\cdot \left(\partial_x\vec{d}\times\partial_y\vec{d}\right) \mathrm{d}S
Chern
number
Nuclear Physics 31, 556 (1962)
Topology
in
momentum space
Two band lattice models
U
T_x
T_y
H(\vec{k})=U+\displaystyle\sum_p \mathrm{e}^{\mathrm{i}\vec{k}\cdot \vec{a}_p}T_p+\mathrm{e}^{-\mathrm{i}\vec{k}\cdot \vec{a}_p}T^\dagger_p
two bands
H(\vec{k})=d_0(\vec{k})\sigma_0+\vec{d}(\vec{k})\cdot\vec{\sigma}
also parametrizes the eigenstates on the Bloch spehre
SSH:The mother of all topological insulators
H=\vec{d}(k)\cdot \vec{\sigma}
\vec{d}(k)=\left(\begin{array}{c}
v+w\cos(k)\\
w\sin(k)\\
0
\end{array}\right)
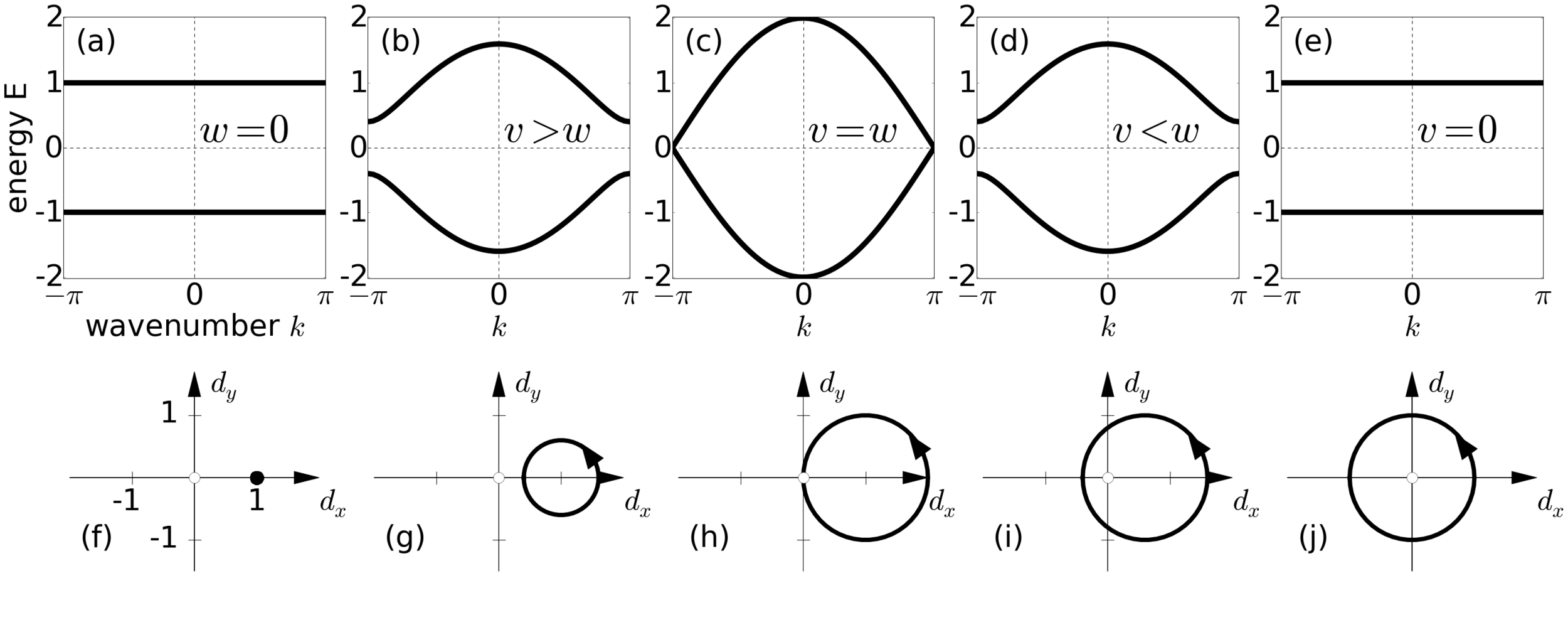
W. P. Su, J. R. Schrieffer, and A. J. Heeger Phys. Rev. Lett. 42, 1698 (1979)
Winding
number
chiral symmetry
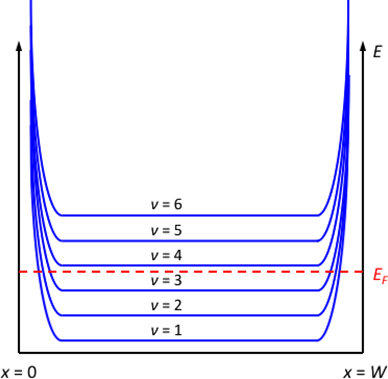
Bulk boundary correspondence
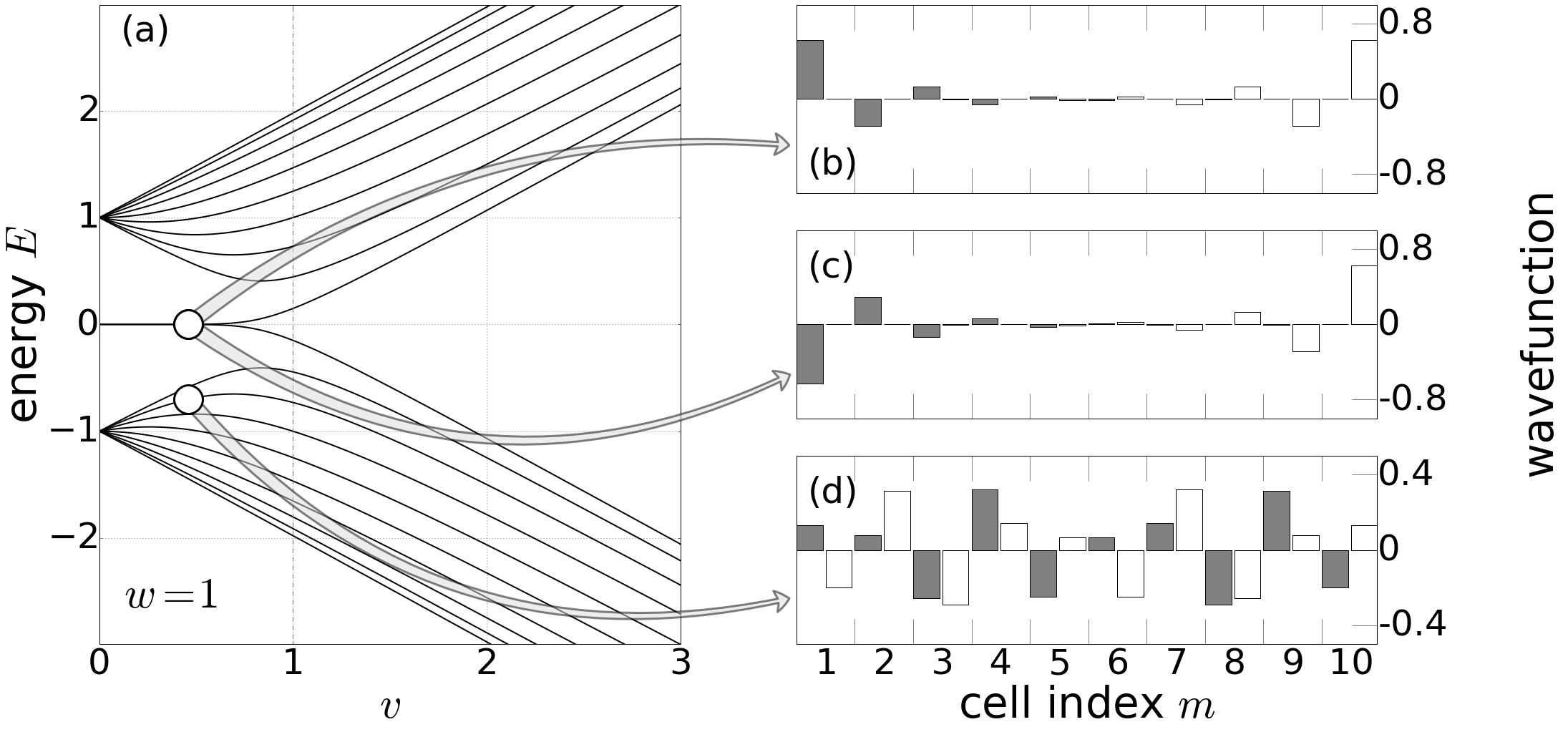
Finite bulk winding number edge states
Chern insulators
\vec{k}=
\left(\begin{array}{c}
k_x\\
k_y
\end{array}\right)
\vec{d}(\vec{k})=
\left(\begin{array}{c}
d_x(\vec{k})\\
d_y(\vec{k})\\
d_z(\vec{k})
\end{array}\right)
BZ
d_x
d_z
d_y
d_x
d_z
d_y
C=0
C=1
"sitting in the origin staring towards infinity"
\rightarrow C
v. Klitzing, Dorda, Pepper Phys. Rev. Lett. 45, 494 (1980)
Haldane Phys. Rev. Lett. 61, 2015 (1988)
Qi, Wu, Zhang Phys. Rev. B 74, 085308 (2006)
Quantum Hall effect & Chern insulators
TRI topological insulators in 2D & 3D
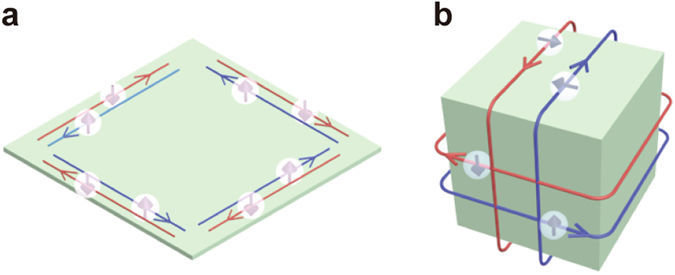
Hasan, Kane Rev. Mod. Phys. 82 3045 (2010)
Topological metals
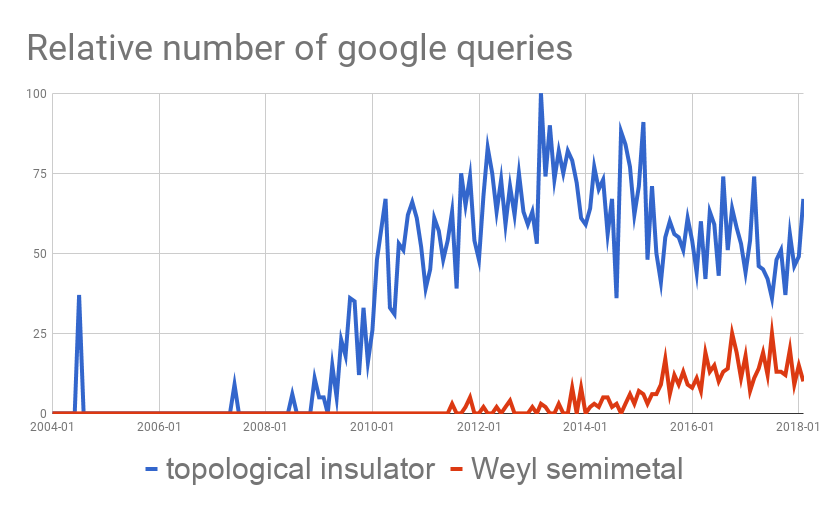
Weyl Semimetals
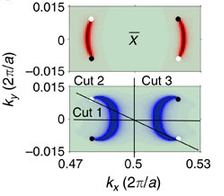
TaAs surface, Nat. Comm. 6, 7373 (2015)
Weyl points+symmetry =nodal lines
\displaystyle H=\left(5t-2t\sum_i \cos(k_i)\right)\sigma_x+2t\sin(k_y)\sigma_y+2t\sin(k_z)\sigma_z
E=0
H=\vec{d}(\vec{k})\cdot \vec{\sigma}
E_\pm=\pm|\vec{d}(\vec{k})|
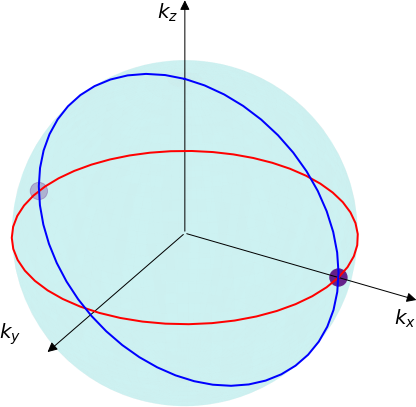
chiral symmetry
Physical realizations and interesting models
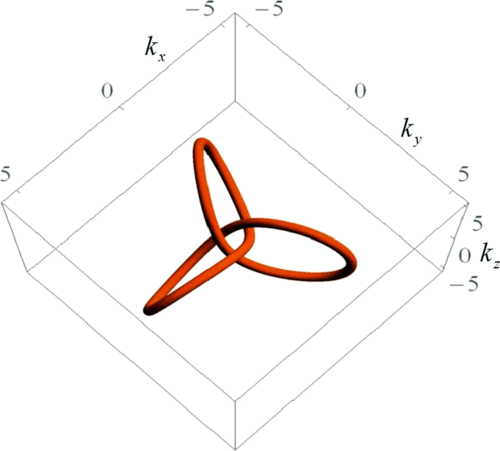
Nodal knots
Phys. Rev. B 96, 201305(R) (2017)
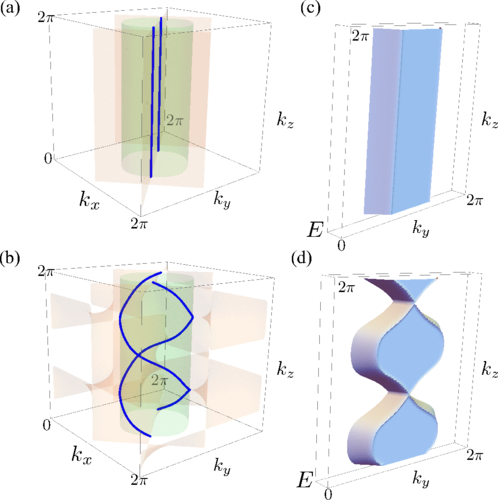
Nodal links
Phys. Rev. B 96, 081114(R) (2017)
A good summary: Adv. Phys. X 3, 1414631 (2018)
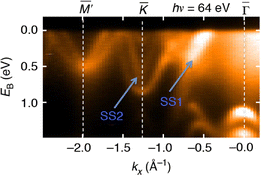
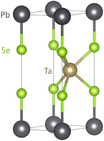
PbTaSe
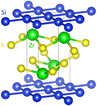
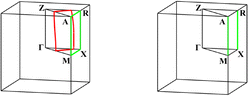
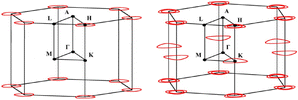
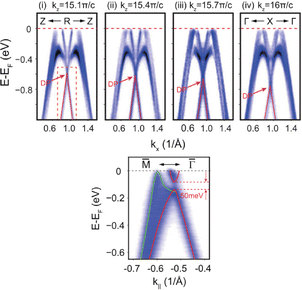
ZrSiS
Magnetic oscillations
in
nodal loop semimetals
SdH & dHvA in 3D: Extremal Fermi surfaces
|\psi_R\rangle
\mathcal{C}
\vec{B}
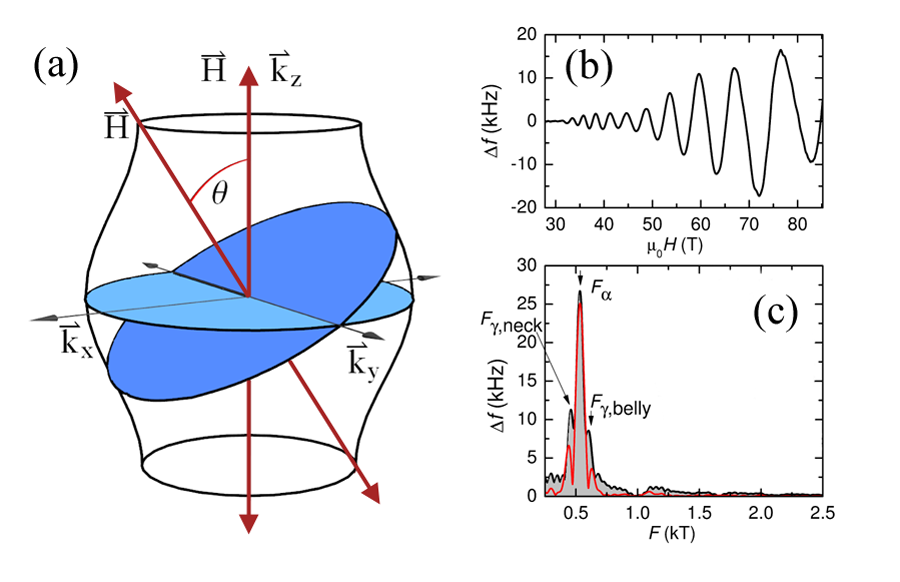
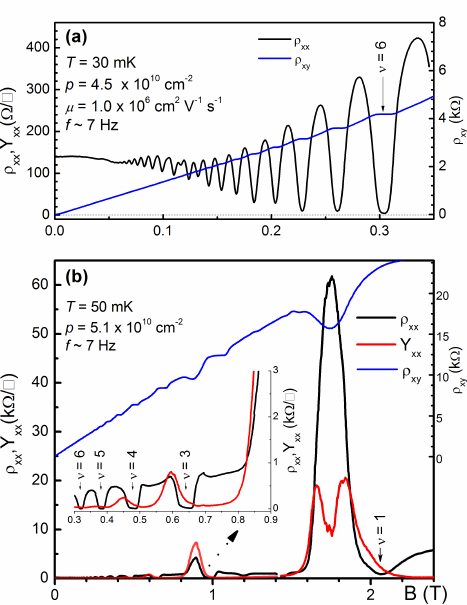
Topological content of magnetic oscillations
\frac{\mathcal{A}(E)\hbar}{eB}=2\pi(n+\gamma)
Onsager quantization condition:
Phil. Mag. 43, 1006 (1952)
Berry's phase:
Proc. R. Soc. Lond. A 392, 45 (1984)
\phi=\mathrm{i}\displaystyle\oint_C\mathrm{d}R\langle \psi_R|\partial_R|\psi_R\rangle
d_x
d_y
d_z
=\pi\left(1-2\gamma\right)
H=\vec{d}_R\cdot\vec{\sigma}
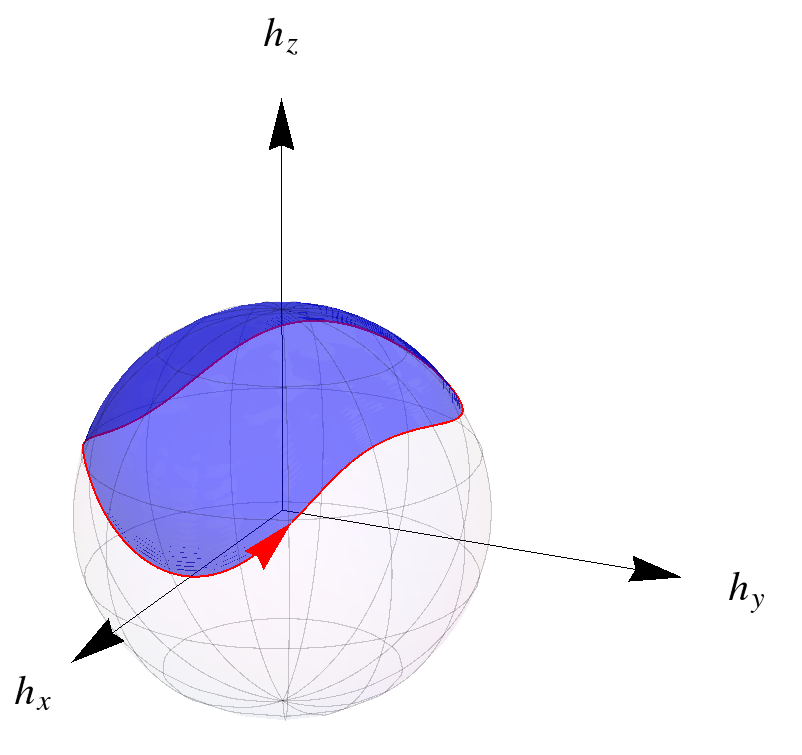
Two band models
Chiral symmetry quantizes Berry's phase!
\varrho(E)=\displaystyle{\sum_n \delta(E-E_n)}
DOS oscillatory in 1/B
nice pedagogical summary for 2D
JN Fuchs https://arxiv.org/pdf/1306.0380.pdf
Simplest case
H=\frac{p^2}{2m}
\vec{A}=By\vec{e_x}
H=\frac{(p_x-eBy)^2+p_y^2+p_z^2}{2m}
E=\frac{\hbar e B}{m}\left (n+\frac{1}{2} \right)+\frac{p_z^2}{2m}
\gamma=\frac{1}{2} !
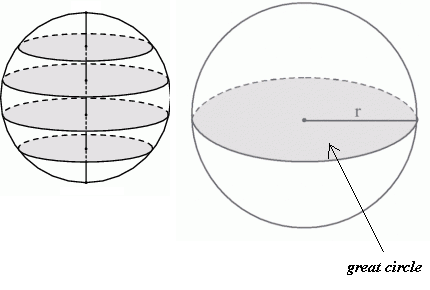
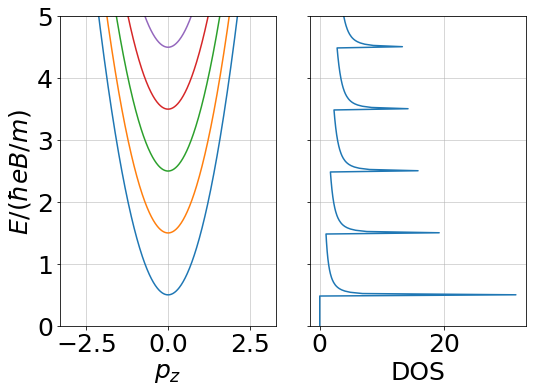
No Berry's phase!
There is "nothing to wind" !
only trivial oscillations!
\vec{B}=-B\vec{e_z}
Weyl semimetals
H=v\vec{p}\cdot\vec{\sigma}
\vec{A}=By\vec{e_x}
H=v\left [(p_x-eBy)\sigma_x+p_y\sigma_y+p_z\sigma_z\right ]
\vec{B}=-B\vec{e_z}
H^2=v^2\left [(eBy)^2+p_y^2+p_z^2\right ]\sigma_0+v^2\hbar eB\sigma_z
H^2=\left [2v^2\hbar eB\left (n+\frac{1}{2}\right)+v^2p_z^2\right ]\sigma_0+v^2\hbar eB\sigma_z
E_n=\pm v\sqrt{2\hbar eB n+p_z^2}
\gamma=0!
non trivial Berry's phase!
"it always winds"
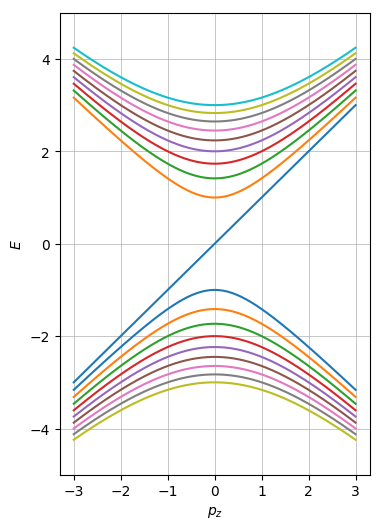
n=0 is special ...
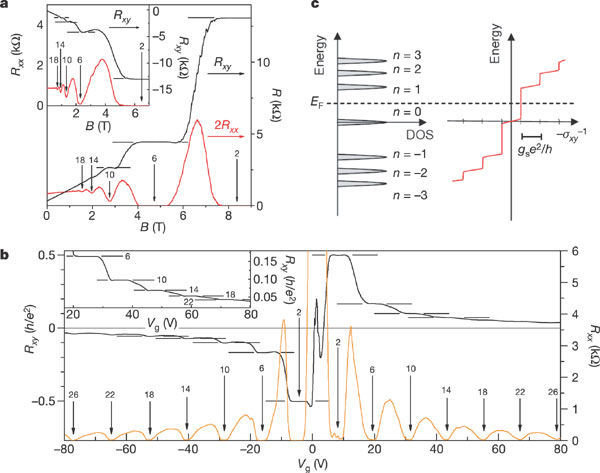
Nature 438, 201 (2005)
Berry phase and the triumph of graphene
H=v\vec{p}\cdot\vec{\sigma}
E=\pm v\sqrt{2\hbar eBn}
\gamma=0,\,\phi=\pi
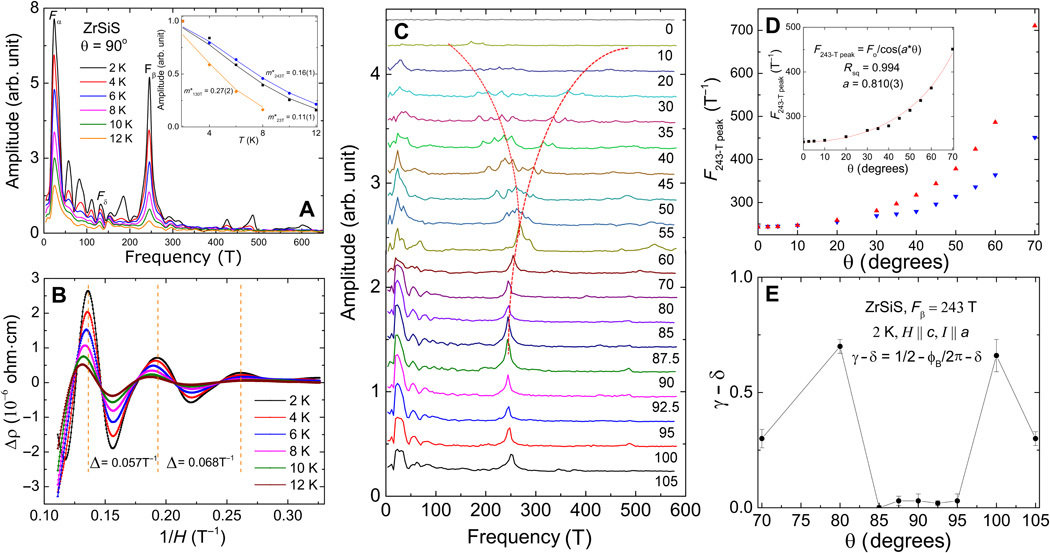
Magnetic oscillations in ZrSiS: experiments
Science Advances 2, e1601742 (2016)
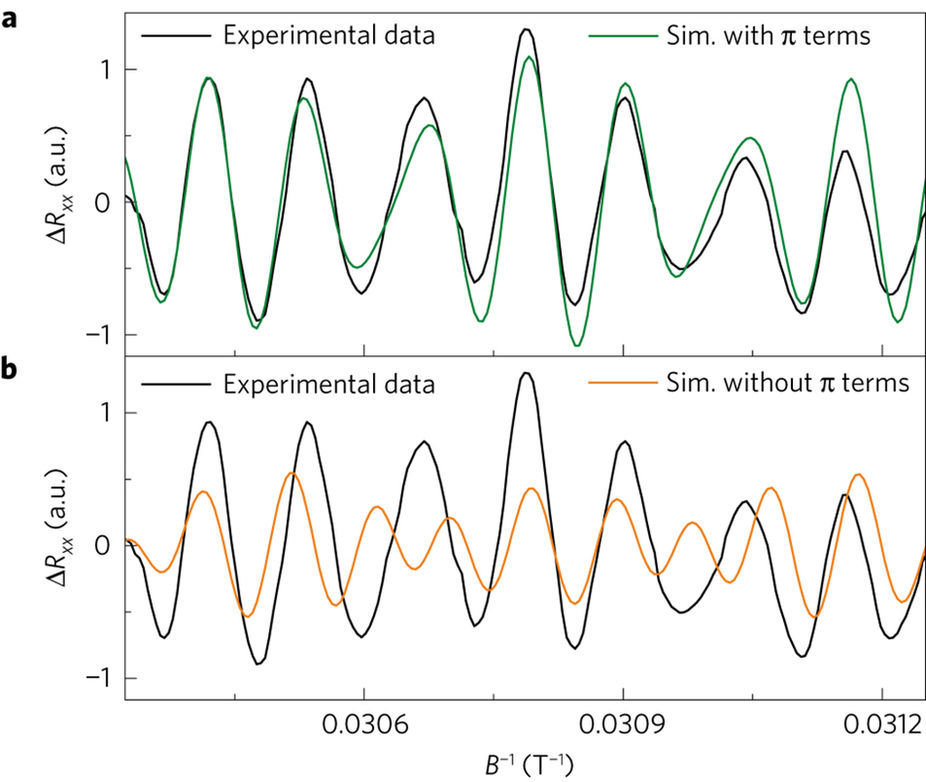
Nature Physics 14, 178 (2018)
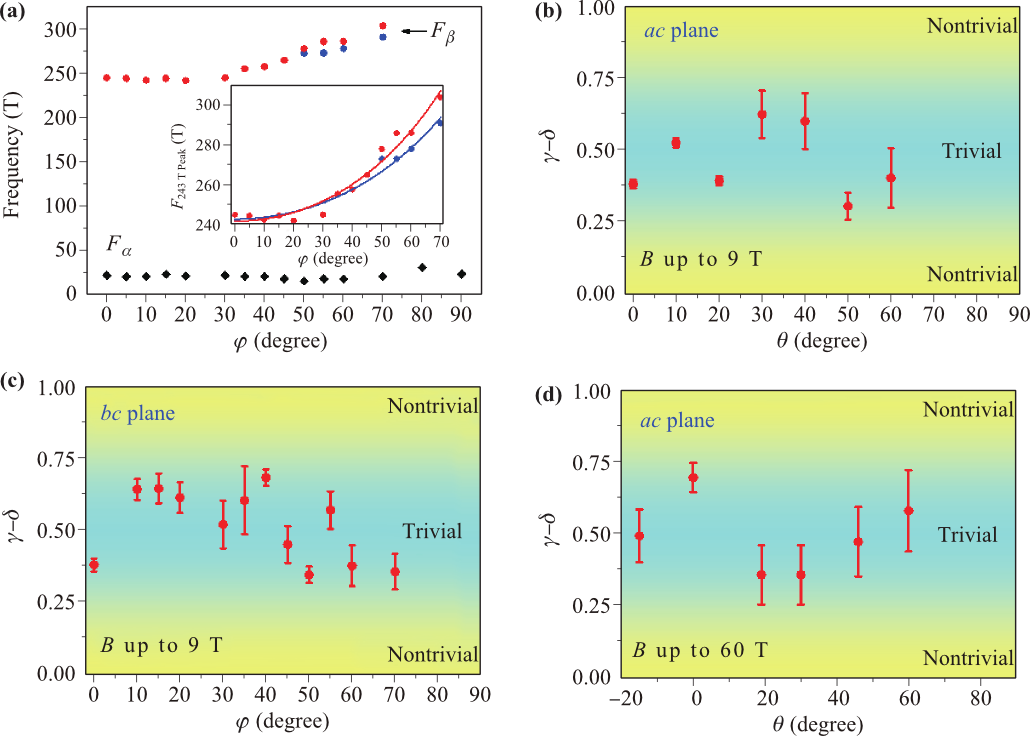
Frontiers of Physics 13, 137201 (2017)
" A transition like this, which is highly sensitive and depends only on a 10° or less change in the magnetic field angle, opens the door to creating new types of devices based on subtle details of the Fermi surface."
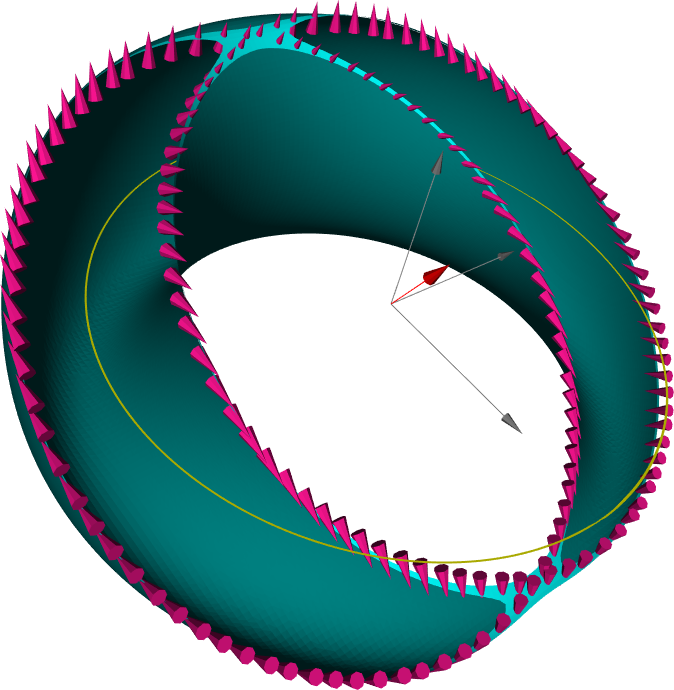
Effective model for nodal loops
\hat{H}=\left(\Delta-\frac{p_x^2+p_y^2}{2m}\right )\sigma_x+v\hat{p}_z\sigma_z=\mathbf{d}(\mathbf{p})\cdot\mathbf{\sigma}
E_\pm=\pm|\mathbf{d}(\mathbf{p})|
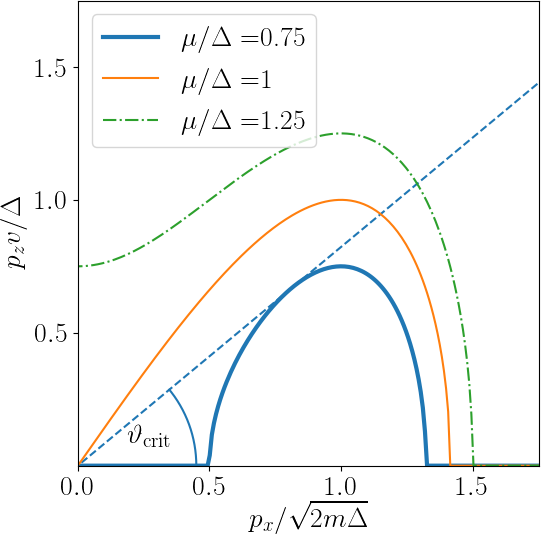
Extremal surfaces of nodal loops
\hat{H}=\left(\Delta-\frac{p_x^2+p_y^2}{2m}\right )\sigma_x+v\hat{p}_z\sigma_z
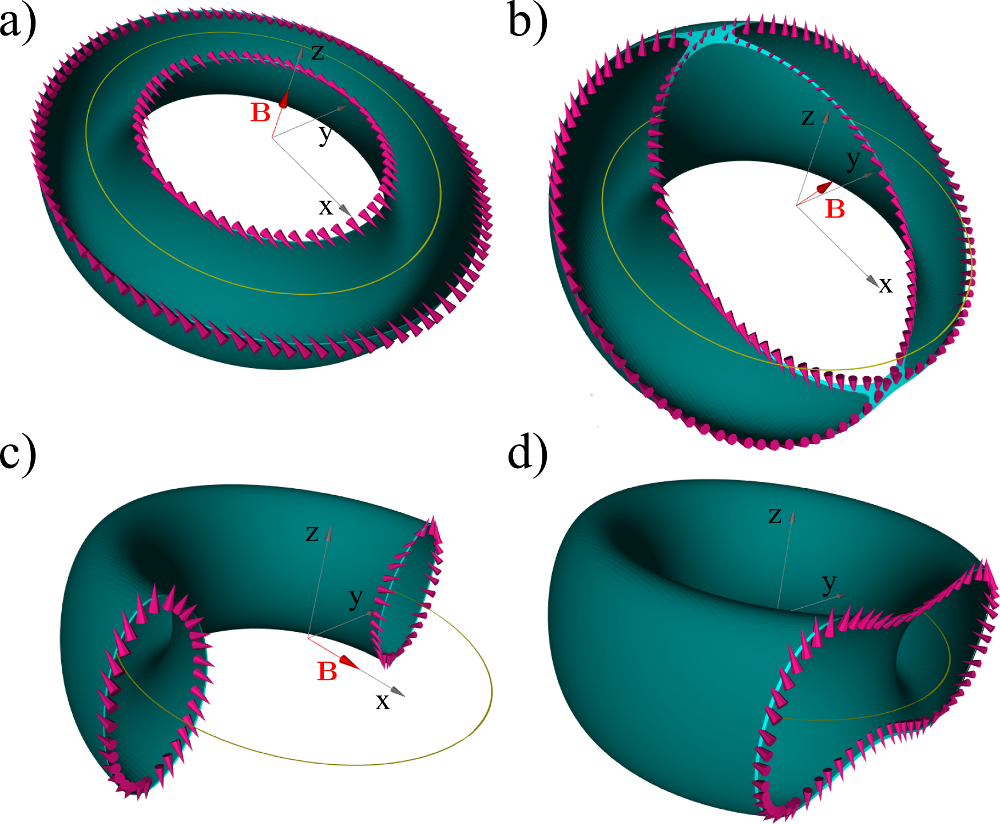
Including magnetic fields
\hat{H}=\left(\Delta-\frac{p_x^2+e^2B^2\left[p_y+z\sin\vartheta-x\cos\vartheta\right]^2}{2m}\right )\sigma_x+v\hat{p}_z\sigma_z
\vartheta=0
E=\pm\sqrt{\left(\Delta-\frac{eB}{m}\left[n+\frac{1}{2}\right]\right)^2+v^2p_z^2}
trivial oscillations
\hat{H}=\left(\Delta-\frac{p_x^2+p_y^2}{2m}\right )\sigma_x+v\hat{p}_z\sigma_z
Magnetic field
perpendicular to the loop
\vec{A}=B(x\cos(\vartheta)-z\sin(\vartheta))\vec{e}_y
E
B
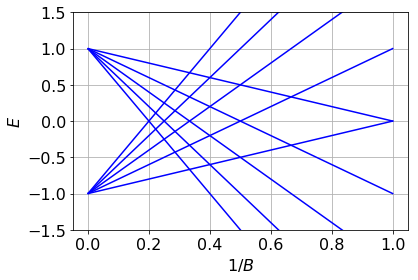
Including magnetic fields
\hat{H}=\left(\Delta-\frac{p_x^2+e^2B^2z^2}{2m}\right )\sigma_x+v\hat{p}_z\sigma_z
\vartheta=\frac{\pi}{2}
E_{n}\approx \left\{\begin{array}{cc}\pm 2\sqrt{\sqrt{\Delta}veBn/\sqrt{2m}}\\ \pm\left(\frac{veB}{\sqrt m}\left(n+\frac 12\right)\right)^{2/3} \end{array}\right.
semiclassics:
topological
trivial
in plane magnetic field
\hat{H}=\left(\alpha-\lambda^2\right )\sigma_x+\hat{p}_\lambda\sigma_z
inspiration: Montambaux et al. Eur. Phys. J. B 72 509 (2009)
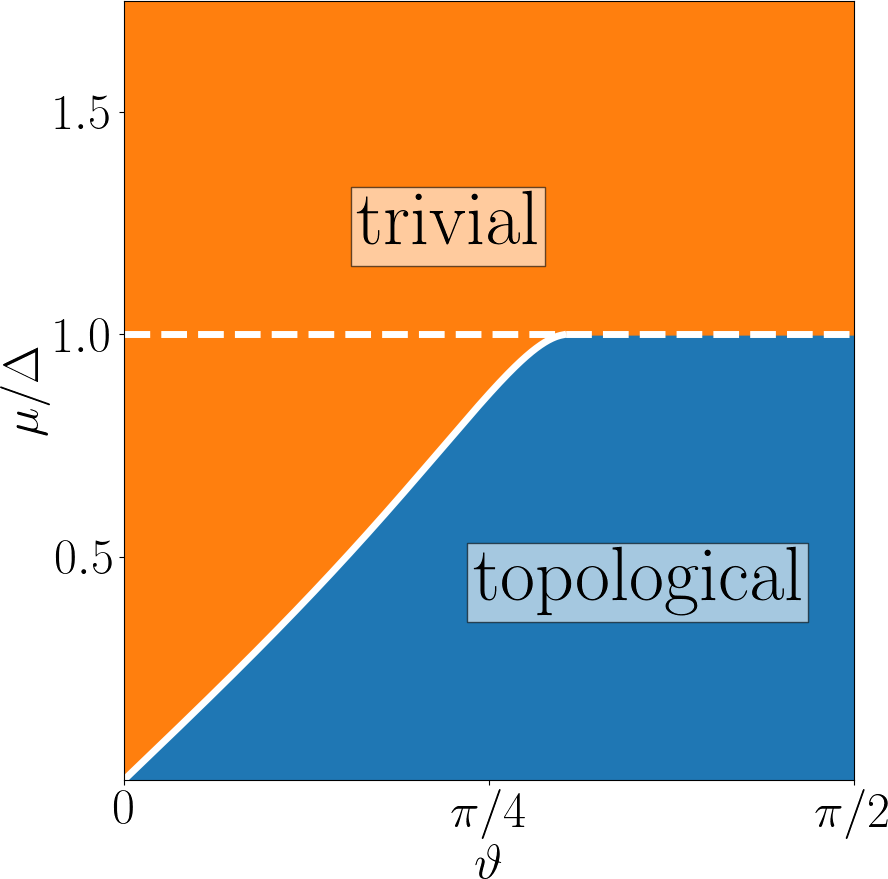
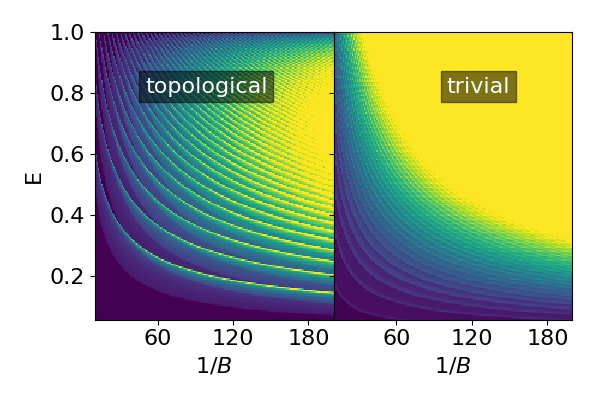
Phase diagram
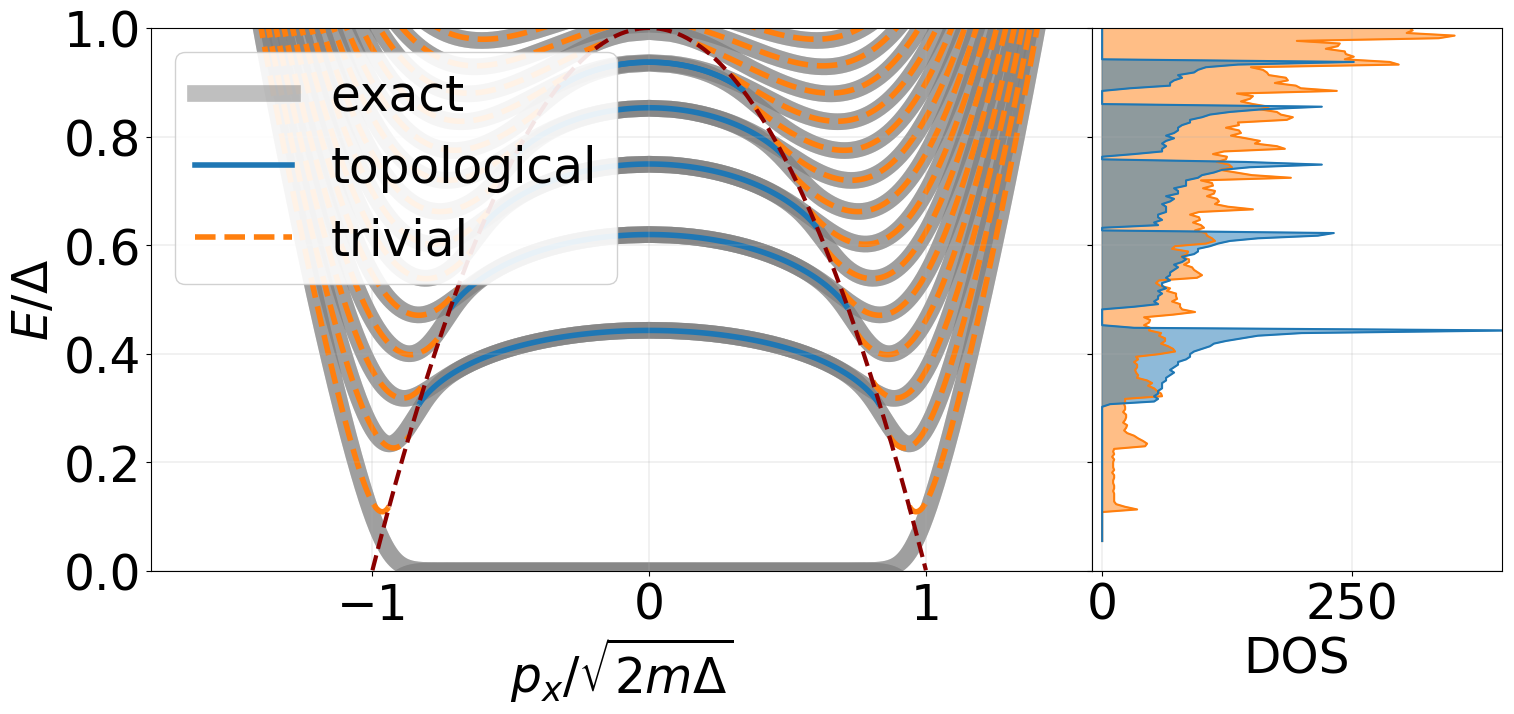
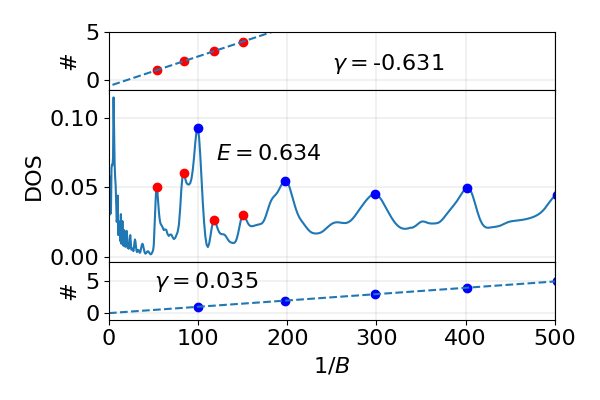
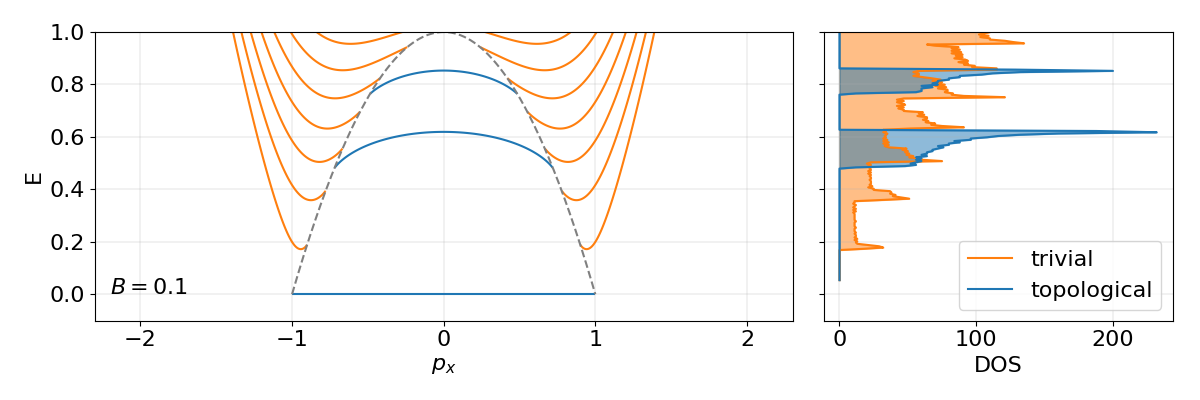
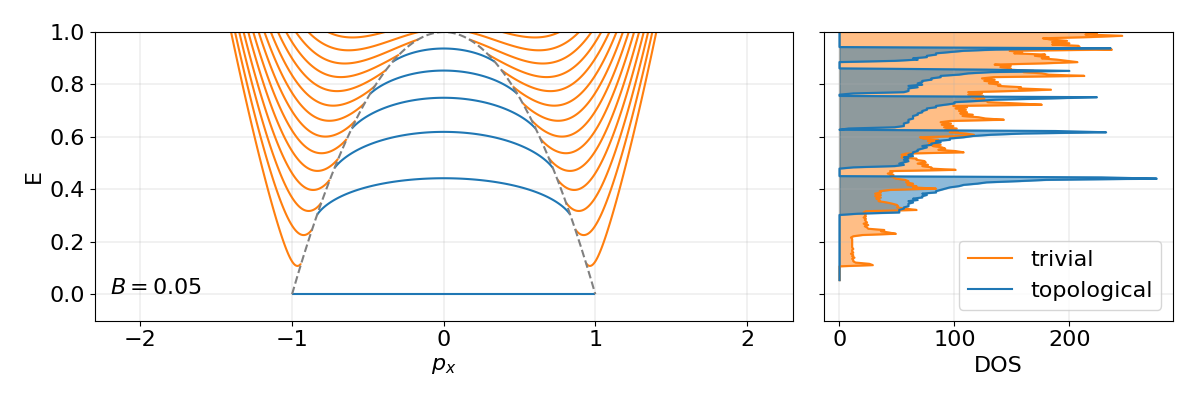
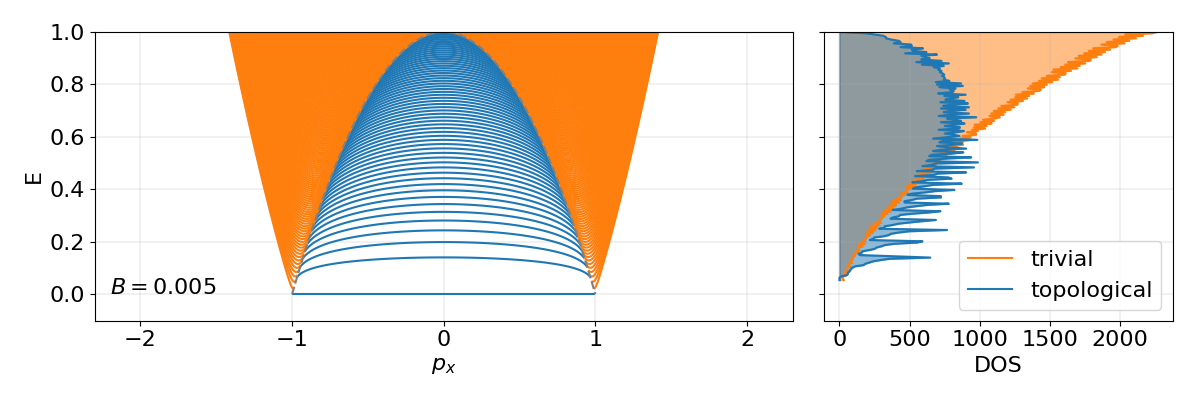
Oscillation spectra
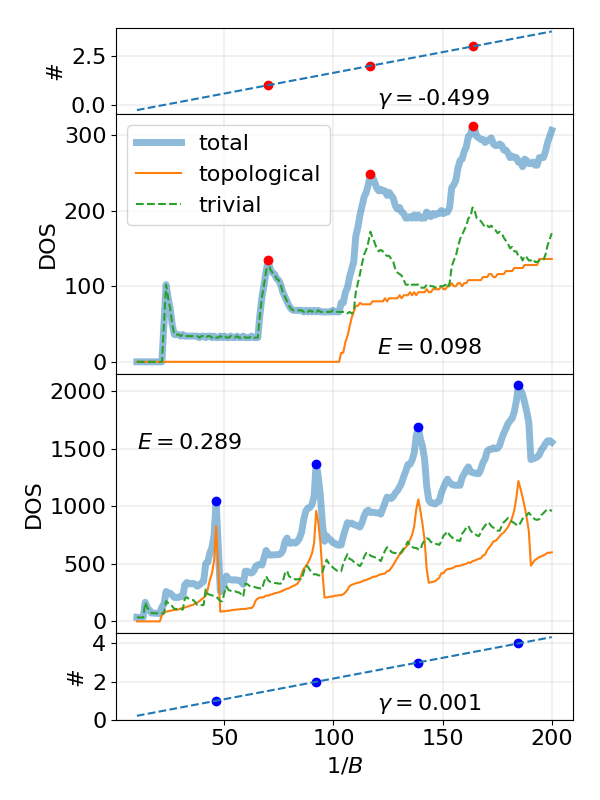
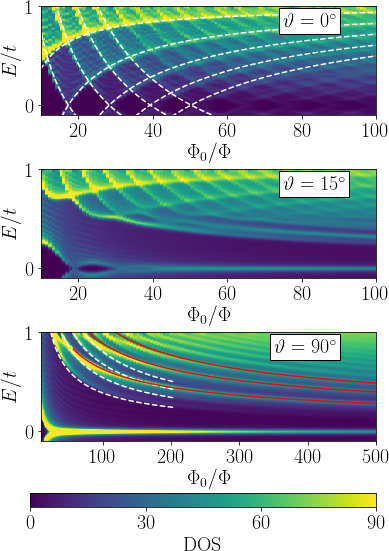
Oscillation spectra
\vartheta=\frac{\pi}{2}
The Team
Balázs Dóra
József Cserti
Alberto Cortijo
Thanks:
details at:
Phys. Rev. B 97, 205107 (2018)
https://arxiv.org/abs/1801.04721
https://github.com/oroszl/nodalloopsemimetal
2017-1.2.1-NKP-2017-00001
A nice, pedagogical summary of topological insulators
:)
https://arxiv.org/abs/1509.02295
A 2D two band insulator with chiral symmetry...
- A) Has always C=0 because of symmetric bands ensures a that the system remains a metal.
- B) Has always C=0 because the torus can never contain the origin and remain an insulator.
- C) Can have C=1 if the torus, the surface defined by d(k) in d-space, intersects the origin.
- D) 2D systems can not have chiral symmetry and thus it is meaningless to define a Chern number for such a system.
We should teach this!
A really good implementation
Minek nevezzelek?
- nodálisvonal-félfém
- nódusvonal-félfém
nodal line semimetals
By László Oroszlány
