A simple electronic ladder model harboring \(\mathbb{Z}_4\) parafermions
Eötvös Loránd University
Budapest University of Technology and Economics
Wigner Research Centre for Physics
Botond Osváth, Gergely Barca, Balázs Dóra,
Örs Legeza, László Oroszlány
The team
Botond Osváth
ELTE
Gergely Barcza Wigner FK
Balázs Dóra
BME
Örs Legeza
Wigner FK
Outline
-
What are Parafermions ? Why should you care?
-
Where did people look for parafermions?
-
Where we look for parafermions ?
-
Where one could look for parafermions ?
Clock models and parafermions
\displaystyle H =-J \sum_{p=1}^{L-1}\omega\hat{\alpha}_{2p}^\dagger\hat{\alpha}_{2p+1}
-f \sum_{p=1}^{L} \omega\hat{\alpha}_{2p-1}^\dagger\hat{\alpha}_{2p}
\Updownarrow
\displaystyle H =-J\sum_{p=1}^{L-1}\hat{\sigma}_{p}^\dagger\hat{\sigma}_{p+1}-f\sum_{p=1}^{L}\hat{\tau}_{p}+\mathrm{h. c.}
\(f=0\rightarrow\) parafermions at the edg, \(\hat{\alpha}_1\) & \(\hat{\alpha}_{2L}\), absent form the Hamiltonian!
The missing two parafermions encode an N-fold degenerate subspace!
\sigma=\left(\begin{array}{ccc}
1 & 0 & 0\\
0 & \Omega & 0\\
0 & 0 & \Omega^{2}
\end{array}\right)\\
\tau=\left(\begin{array}{ccc}
0 & 0 & 1\\
1 & 0 & 0\\
0 & 1 & 0
\end{array}\right)\\
\Omega=\text{e}^{\text{i}2\pi/N}=\omega^2
N=3 Clock model
Jordan-Wigner
\displaystyle\hat{\alpha}_{2p-1} =\hat{\sigma}_{p}\prod_{q < p}\hat{\tau}_{q} \\
\hat{\alpha}_{2p} =-\omega\hat{\tau}_{p}\hat{\sigma}_{p}\prod_{q < p}\hat{\tau}_{q}\\
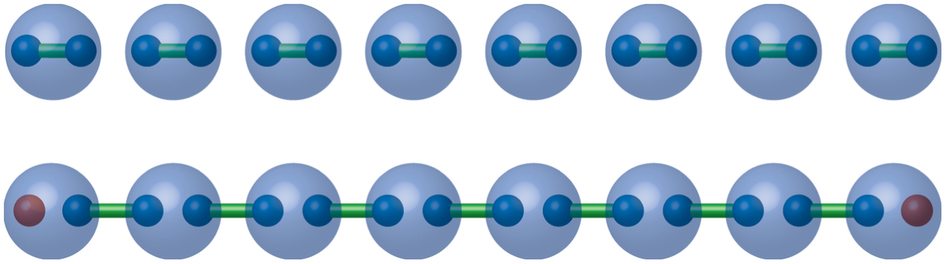
Parafermion
\hat{\alpha}^N_p=\hat{1},\hat{\alpha}_p^\dagger=\hat{\alpha}^{N-1}_p
\hat{\alpha}_p\hat{\alpha}_q=\Omega^{\mathrm{sign}(q-p)}\hat{\alpha}_q\hat{\alpha}_p
Majoranas vs. parafermions
- Two Majorana zero modes encode a doubly degenerate subspace.
- Majorana modes can be potentially realized in non-interacting systems. (i.e. mean-field description is sufficient)
- With braiding alone, Majorana modes can realize nontrivial unitary operations, but no entangling qbit gates.
- Two \(\mathbb{Z}_n\) parafermions encode an \(n\)-fold degenerate subspace.
- Parafermions need interaction. (i.e. mean-field description is not sufficient)
- \(\mathbb{Z}_{even}\) parafermions can realize entangling gates just with braiding!
- \(\mathbb{Z}_{odd}\) parafermions: route to universality
A.Hutter, D. Loss Phys. Rev. B 93, 125105 (2016)
Parafermion signatures
- Robustness against disorder
- Highly (>2) degenerate groundstate
- Localized zero-energy excitations
- Nontrivial (fractional) Josephson effect
\(\mathbb{Z}_n\rightarrow 2n\pi\) periodic
J. Alicea, P. Fendley Annu. Rev. Condens. Matter Phys. 7,119 (2016.)
Possible experimental blueprints
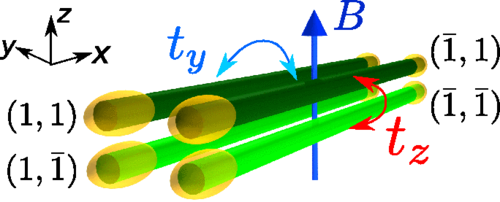
J. Klinovaja and D. Loss
Phys. Rev. Lett. 112, 246403 (2014)
Phys. Rev. B 90, 045118 (2014)
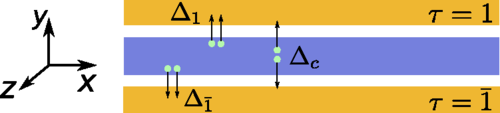
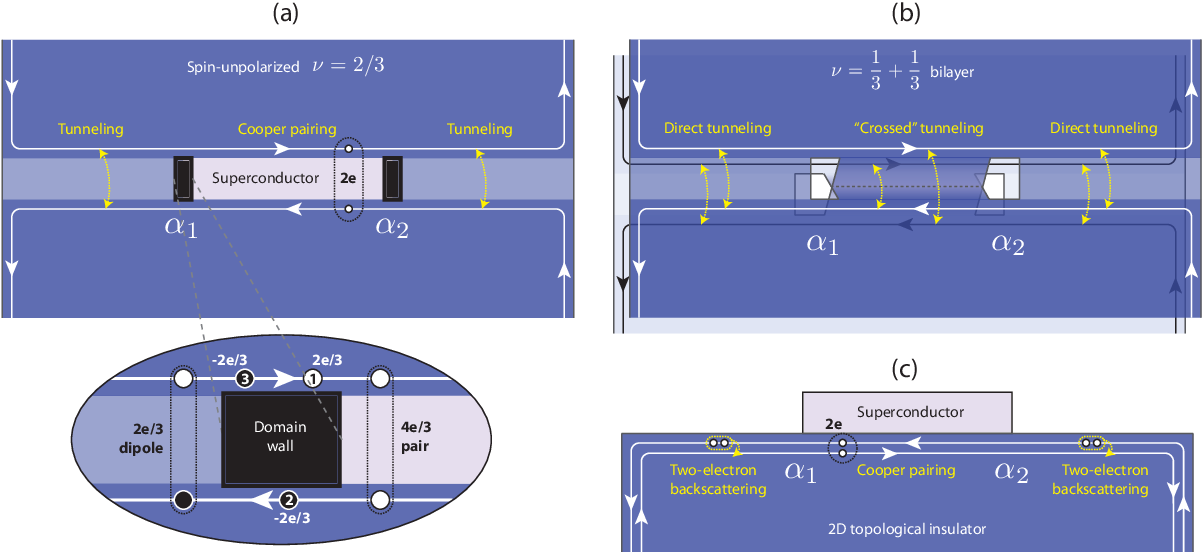
J. Alicea, P. Fendley Annu. Rev. Condens. Matter Phys. 7,119 (2016.)
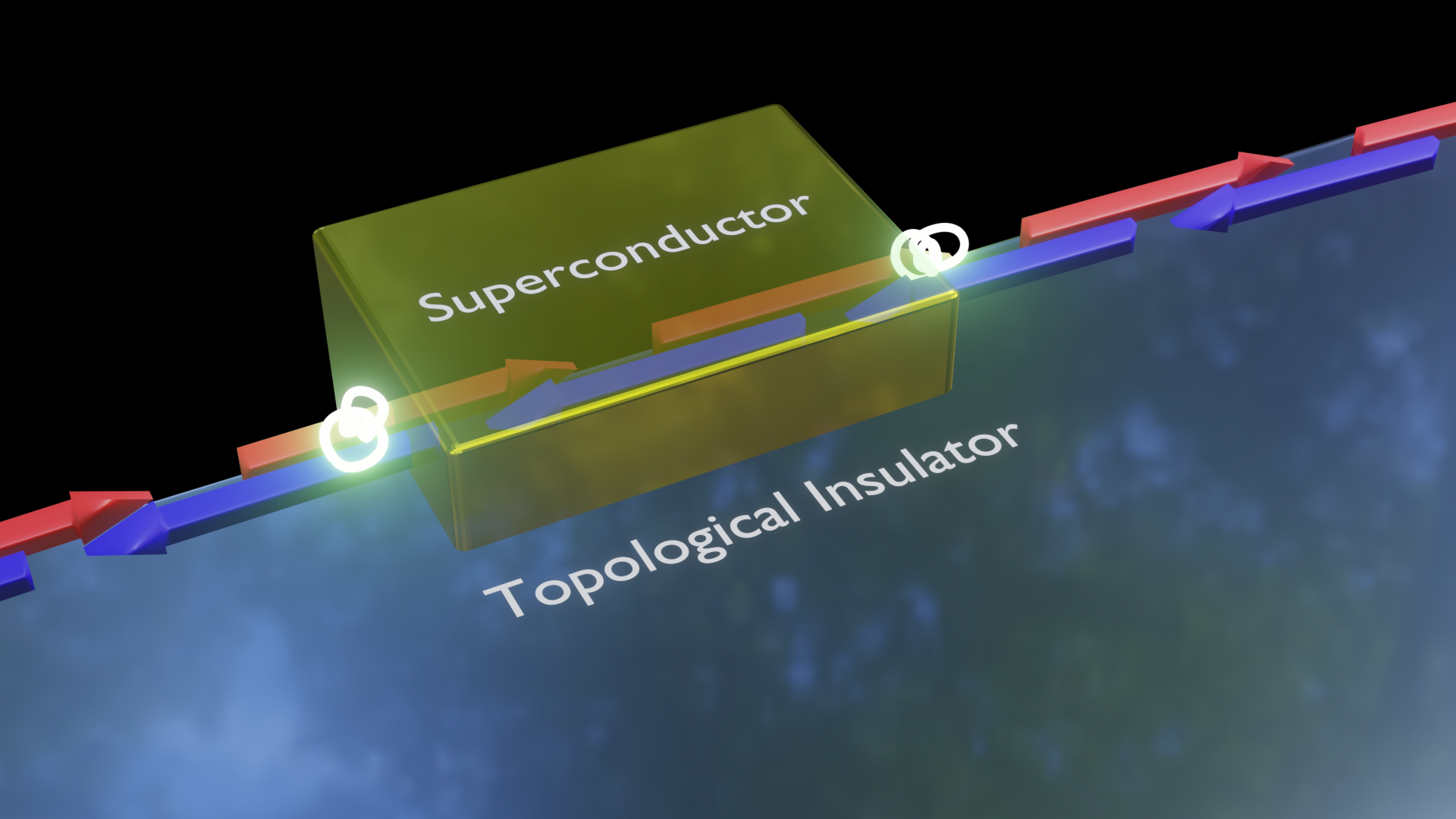
Parafermions at TI edge
F. Zhang, C. L. Kane, Phys. Rev. Lett., 113, 036401 (2014).
C. P. Orth et al. Phys. Rev. B, 91, 081406 (2015).
J. Alicea, P. Fendley Annu. Rev. Condens. Matter Phys. 7,119 (2016.)
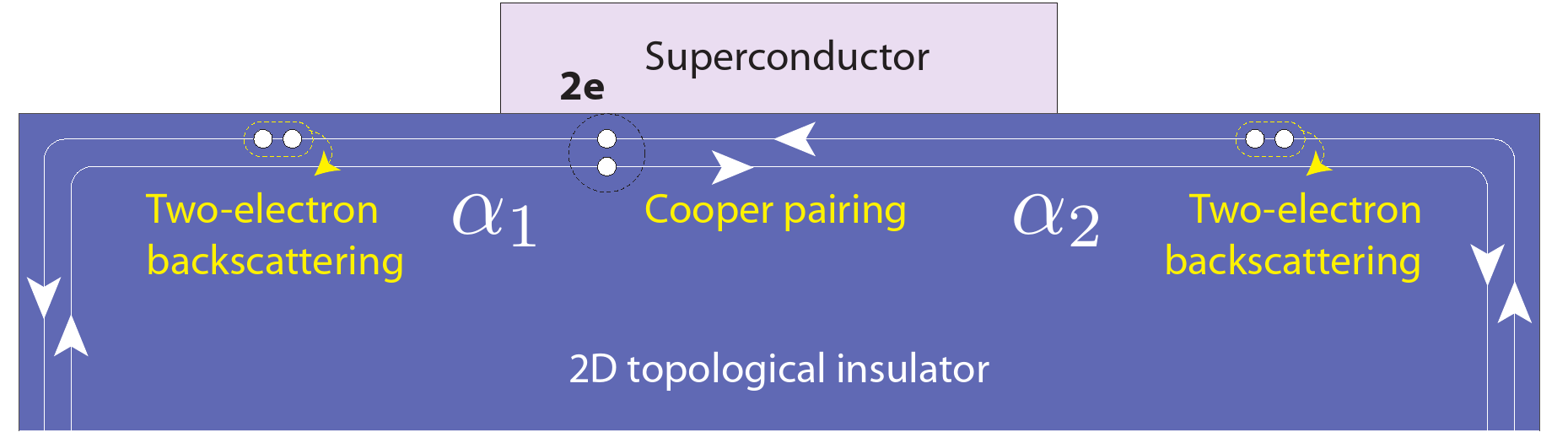
goal: microscopic model + DMRG
bosonised models
ITensor
Budapest DMRG
A model for 2DTI that can be digested by DMRG?
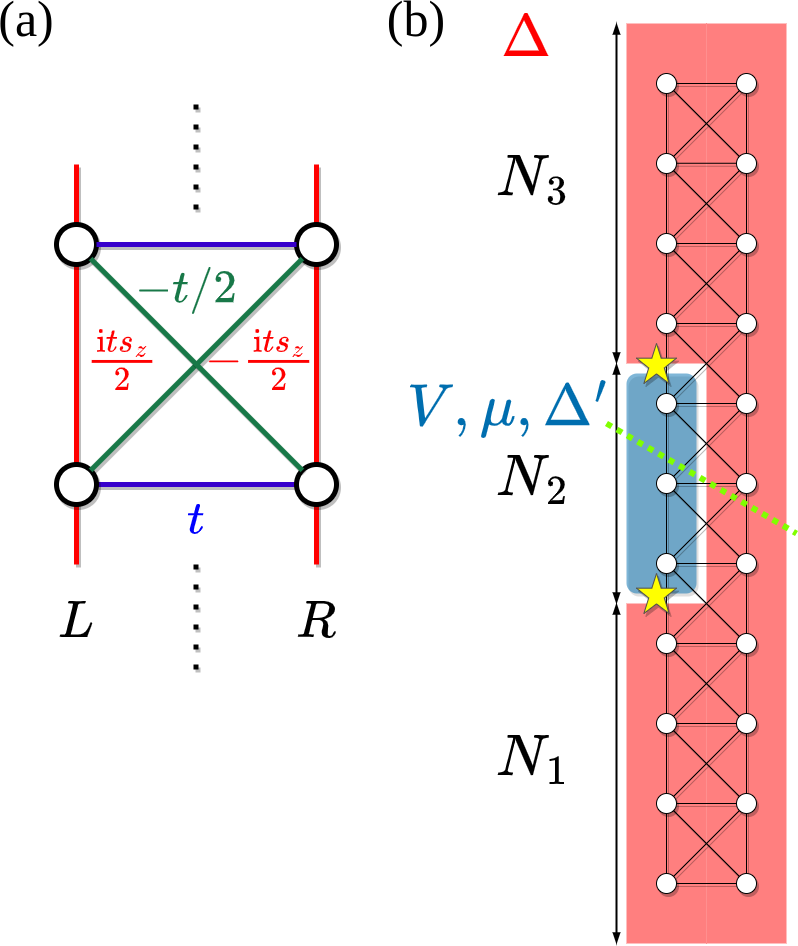
The model
- two "disconnected edges" \(\zeta = {L,R}\)
- explicit superconductivity and interactions
- time reversal symmetry
\displaystyle H_k=\sum_{m\sigma}\left(\begin{array}{cc}
c_{mL\sigma}^{\dagger} & c_{mR\sigma}^{\dagger}\end{array}\right)\left(\begin{array}{cc}
-\mu & t\\
t & -\mu
\end{array}\right)\left(\begin{array}{c}
c_{mL\sigma}\\
c_{mR\sigma}
\end{array}\right)\quad\quad\quad \quad \\
-\frac{t}{2}\sum_{m\sigma}\left[\left(\begin{array}{cc}
c_{m+1L\sigma}^{\dagger} & c_{m+1R\sigma}^{\dagger}\end{array}\right)\left(\begin{array}{cc}
\text{i}\sigma & 1\\
1 & -\text{i}\sigma
\end{array}\right)\left(\begin{array}{c}
c_{mL\sigma}\\
c_{mR\sigma}
\end{array}\right)+\text{h.c.}\right]
H=H_k+H_{sc}+H_{int}
\displaystyle
H_{sc} =\sum_{m\zeta}\Delta_{m\zeta}\left[c_{m\zeta\uparrow}^{\dagger}c_{m\zeta\downarrow}^{\dagger}+\text{h.c.}\right]
\quad \quad \quad \quad \quad \quad
\\
H_{int}=\sum_{m\zeta}V_{m\zeta}\left [c^\dagger_{m\zeta\uparrow}c_{m\zeta\downarrow}c^\dagger_{(m+1)\zeta\uparrow}c_{(m+1)\zeta\downarrow}+\text{h.c.}\right]
H_k\approx ps_z\zeta_z
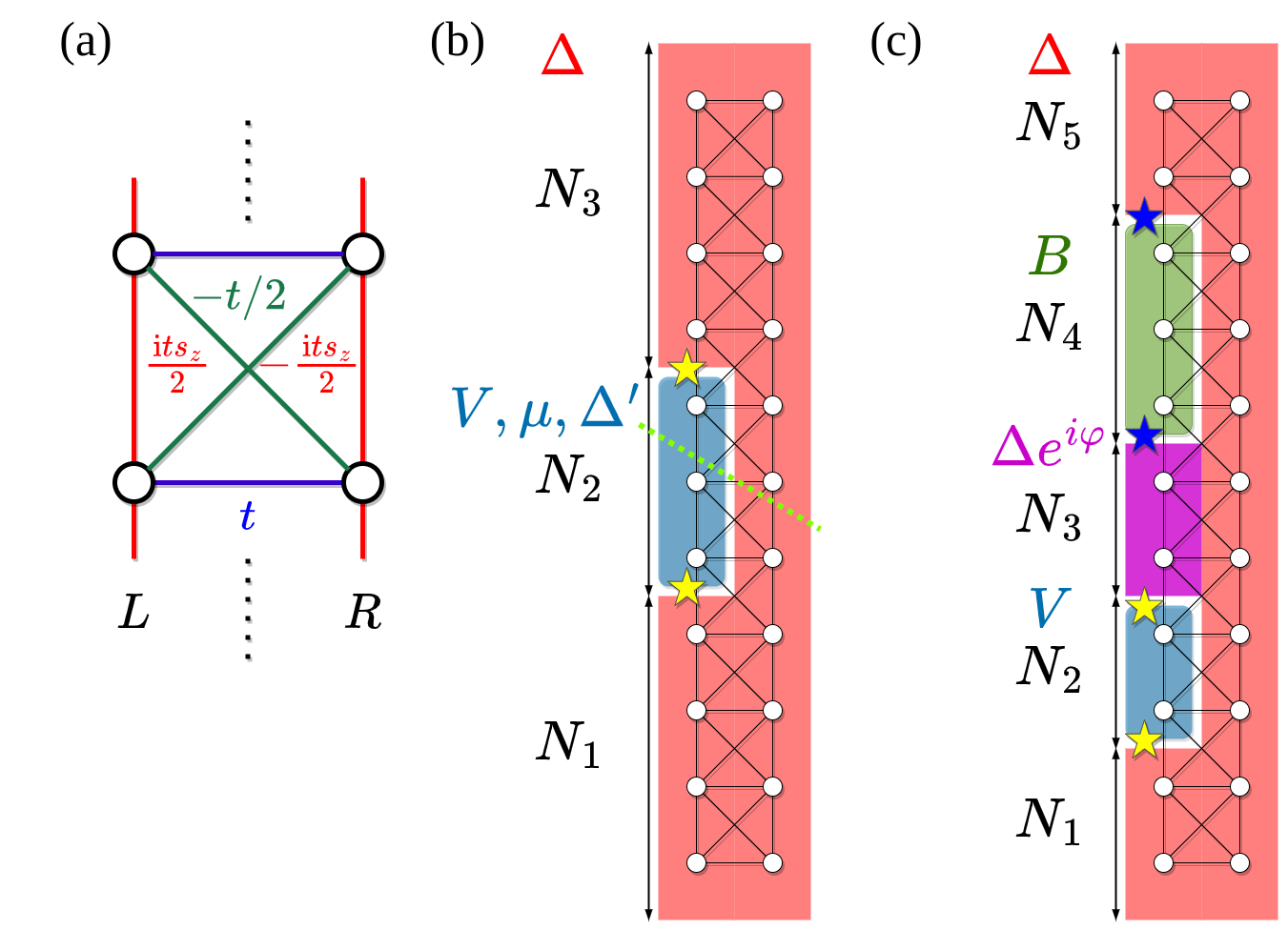
L
R
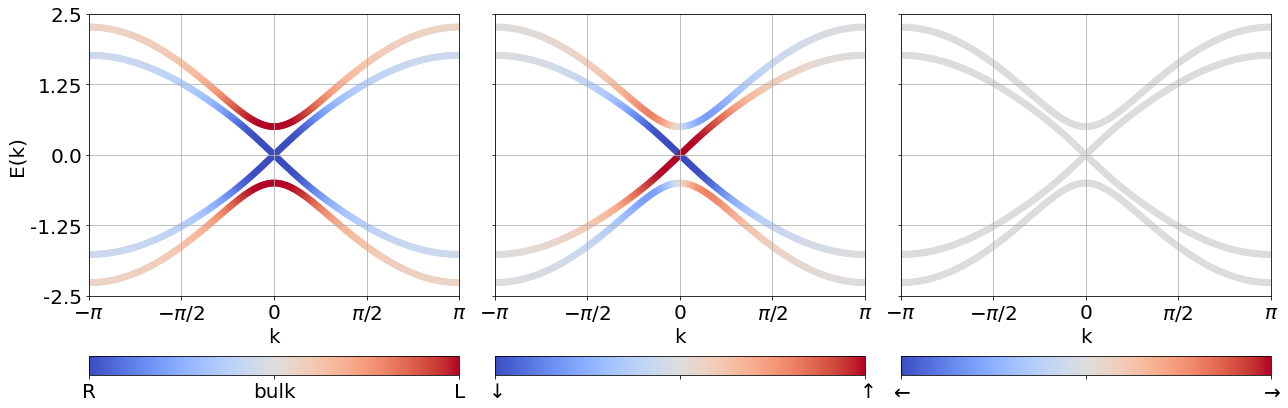
Single particle spectrum
small \(B_y\) on the left for better visibility
B_{y}\neq 0
L
R
We still have Majoranas !
B_{y}\neq 0
L
R
\Delta\neq 0
V=0
Fu, Kane Phys. Rev. Lett. 100, 096407 (2008)
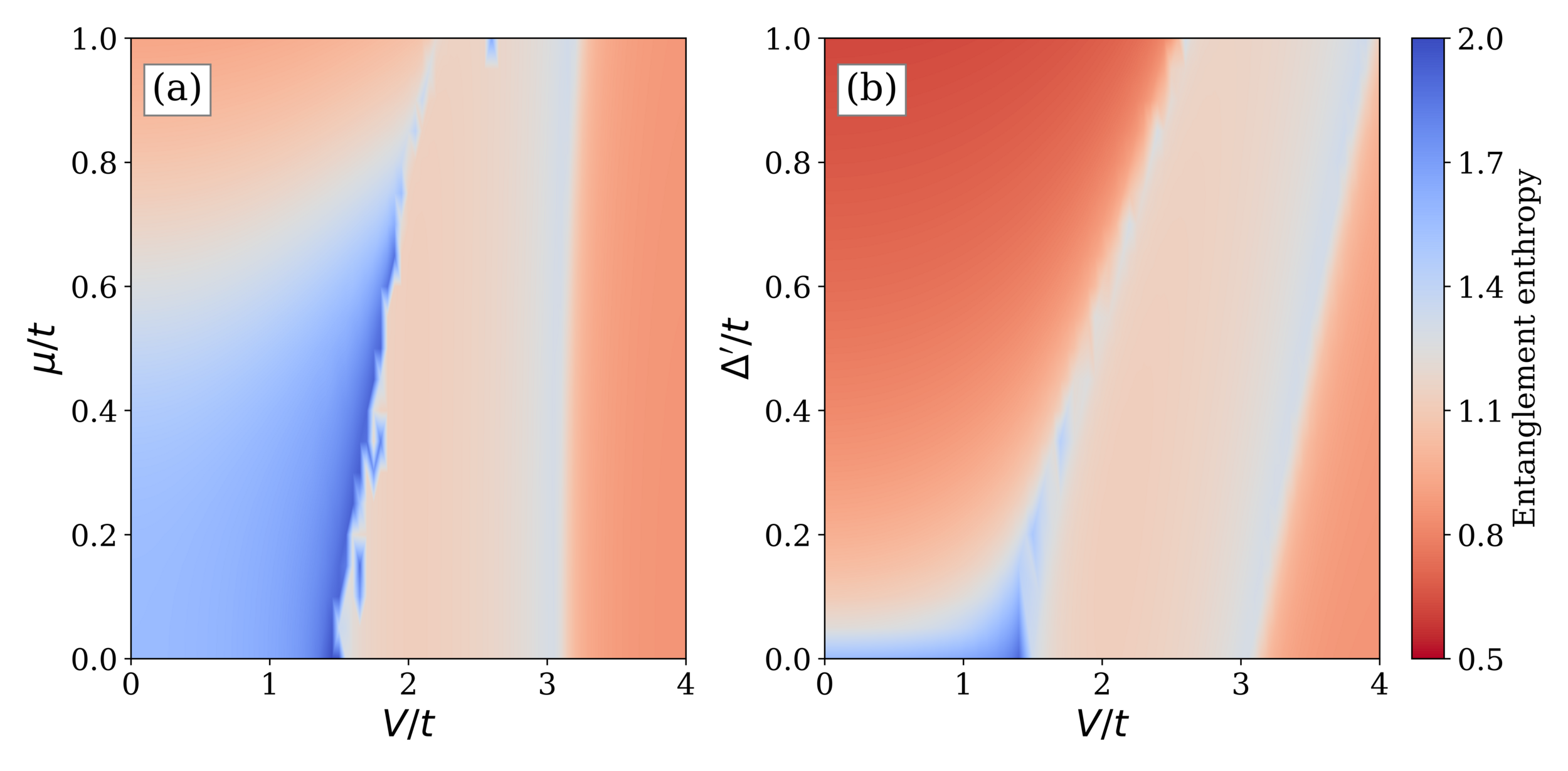
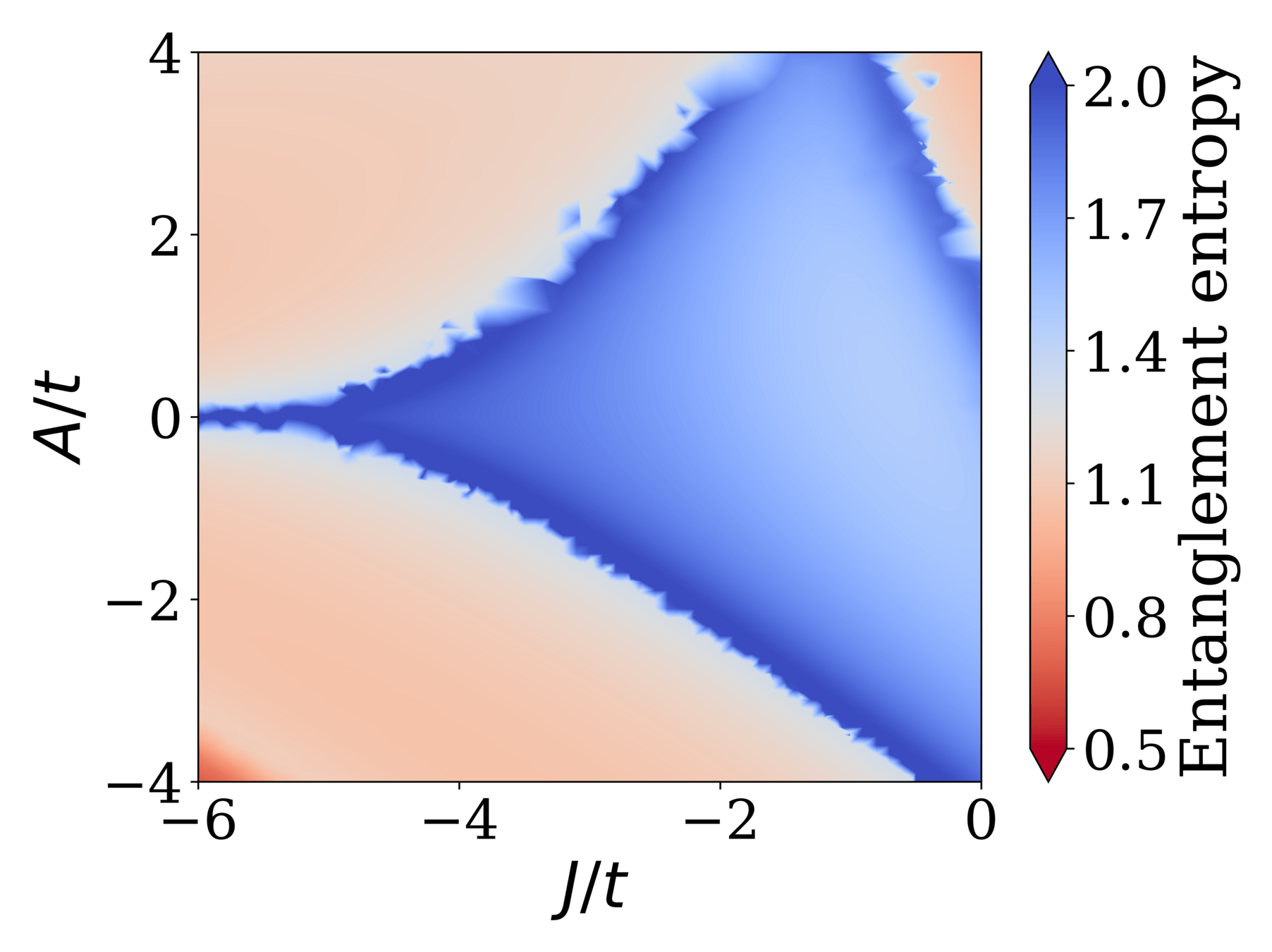
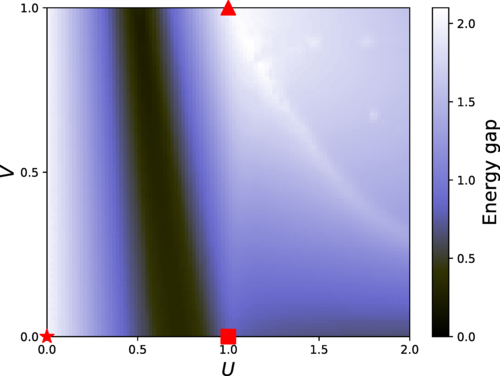
Finite-size DMRG calculations: phase diagram
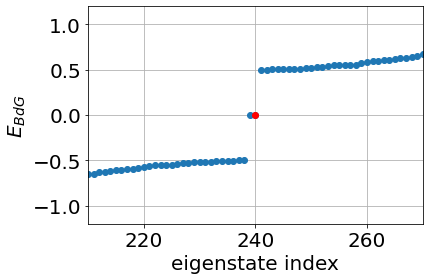
Finite-size DMRG calculations: excitation spectrum
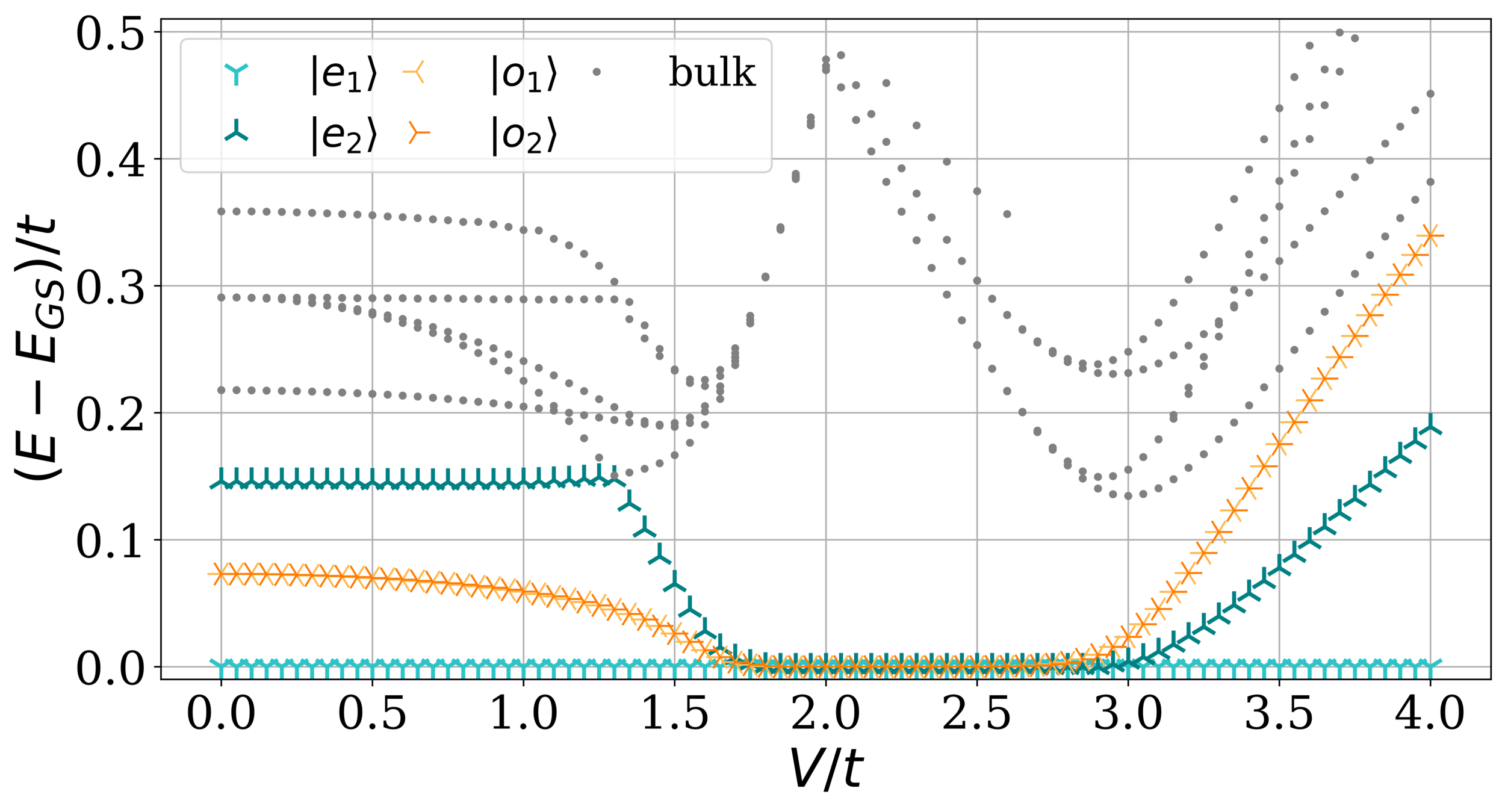
\(\mu=\Delta'=0\)
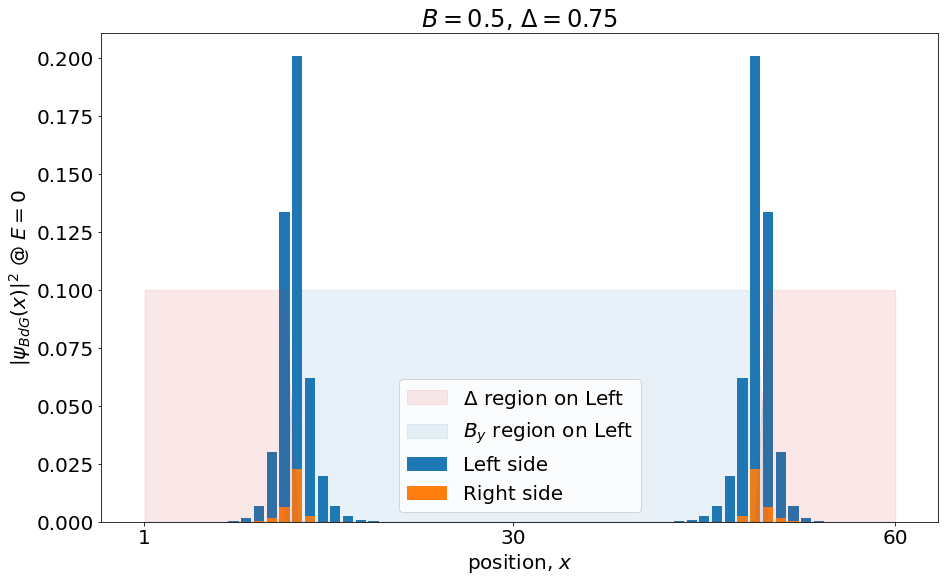
Finite-size DMRG calculations: local quantities
\( \langle GS_p | n_i | GS_q \rangle \propto \delta_{pq} \)
\displaystyle H_{int}=\sum_{m\zeta}V_{m\zeta}\left [c^\dagger_{m\zeta\uparrow}c_{m\zeta\downarrow}c^\dagger_{(m+1)\zeta\uparrow}c_{(m+1)\zeta\downarrow}+\text{h.c.}\right]\\
= \sum_{m,\zeta}\frac{V_{m,\zeta}}{2}\left[ S^x_{m,\zeta}S^x_{m+1,\zeta}-S^y_{m,\zeta}S^y_{m+1,\zeta}\right]
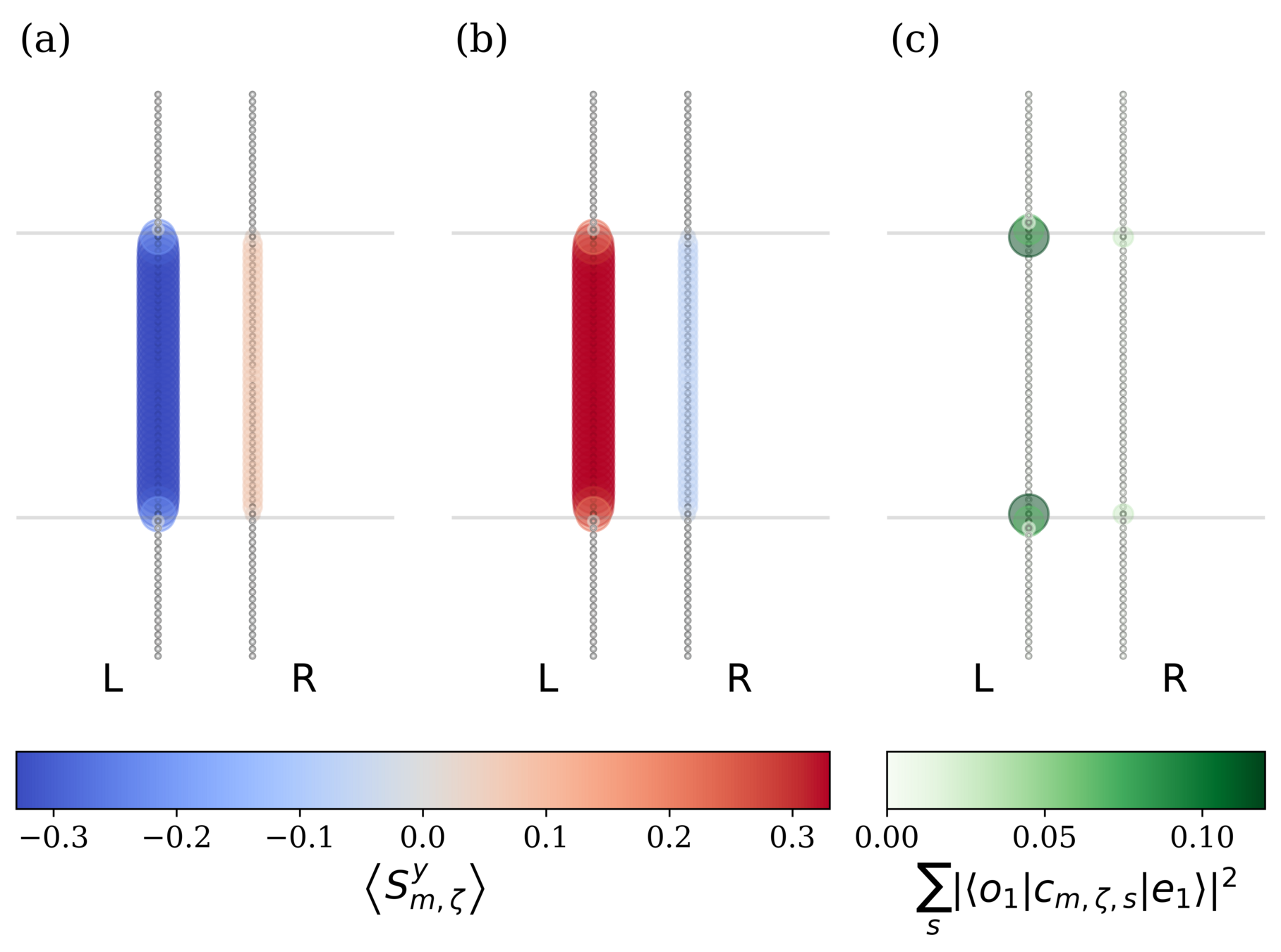
\(\mu=\Delta'=0\), \(V/t=2.2\)
Y. Vinkler-Aviv, et al. Phys. Rev. B 96, 195421 (2017)
Finite-size DMRG calculations: Josephson spectrum
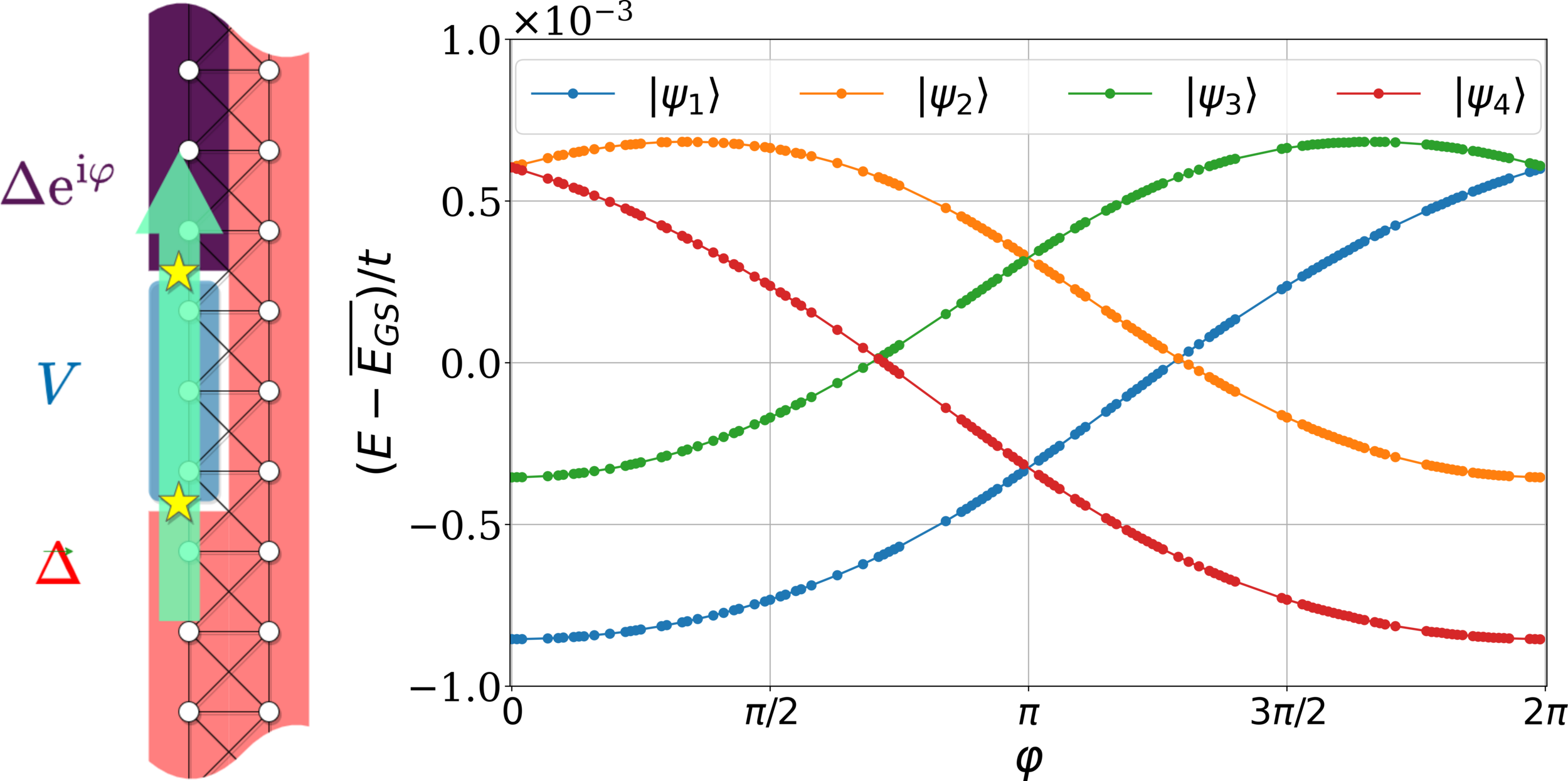
Single anisotropy term is sufficient !
isotropic exchange
anisotropic exchange
\begin{align*}
H_{int}=\sum_{m,\zeta} &J \mathbf{S}_{m,\zeta}\cdot\mathbf{S}_{m+1,\zeta}\\
+ &A S^x_{m,\zeta}S^x_{m+1,\zeta}
\end{align*}
Parafermion signatures
- Robustness against disorder ✓
- Fourfold degenerate groundstate ✓
- Localized zero-energy excitations ✓
- Nontrivial (fractional) Josephson effect ✓
\(\mathbb{Z}_4\rightarrow 8\pi\) periodic
J. Alicea, P. Fendley Annu. Rev. Condens. Matter Phys. 7,119 (2016.)
Quantum dot arrays for parafermions!!
Hsiao et al.
Phys. Rev. X 14, 011048 (2024)
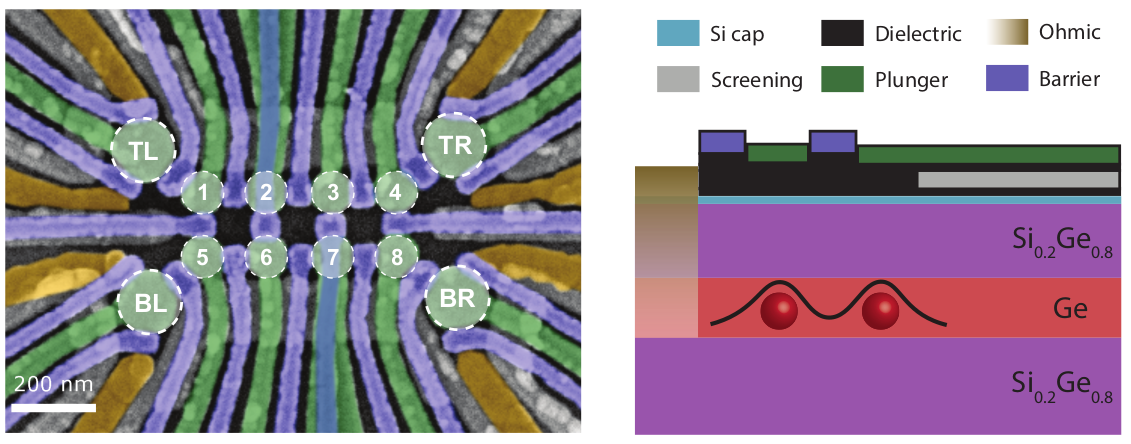
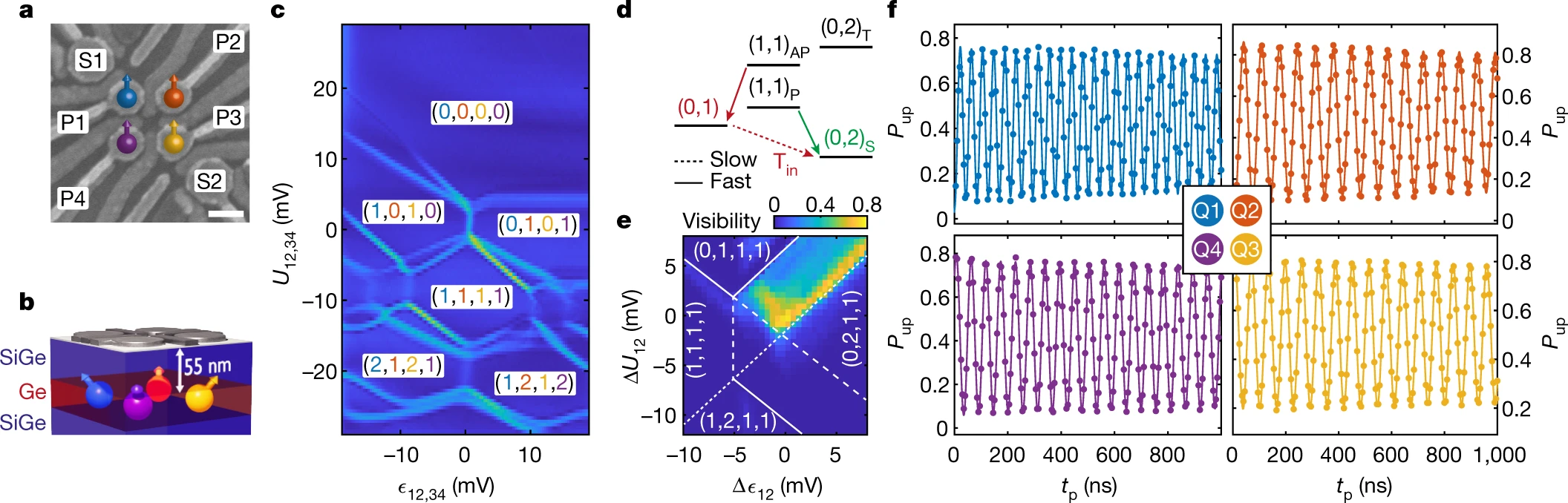
Hendrickx et al.
Nature 591, 580 (2021).
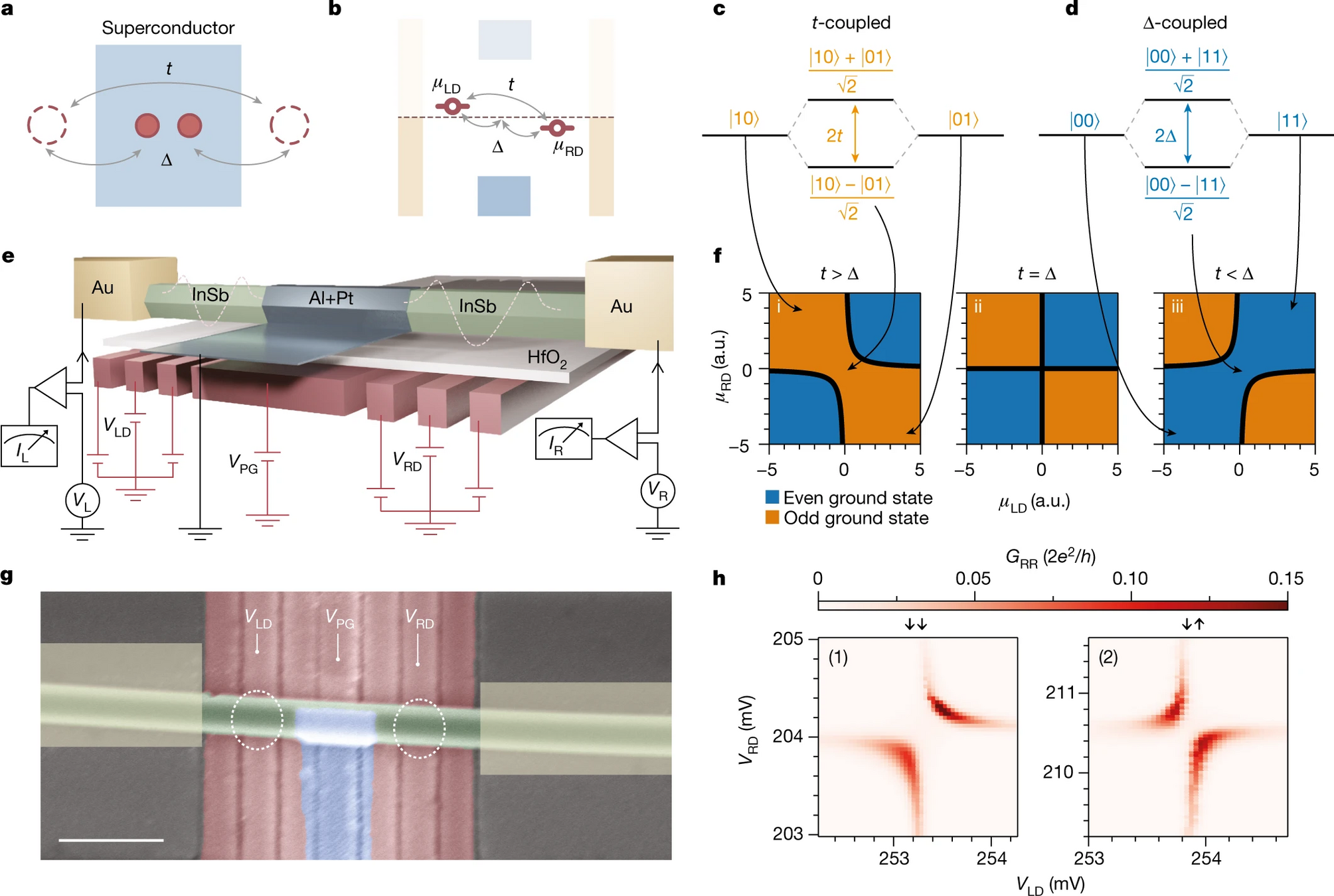
Dvir et al.
Nature 614, 445 (2023)
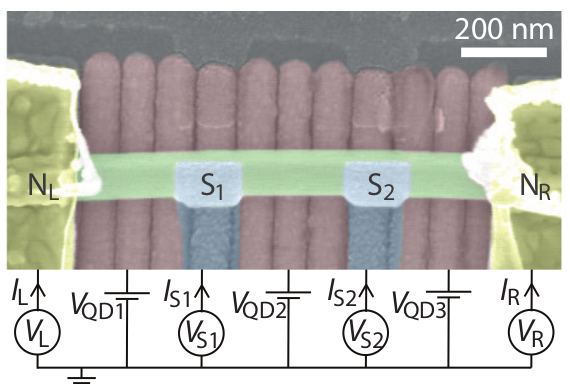
Bordin et al. Phys. Rev. Lett. 132, 056602 (2024)
Summary
- Simple ladder model capable to capture physics at a single edge of a TI.
-
Interactions and superconductivity are explicitly taken into account through DMRG calculations.
-
Fourfold degeneracy and localized interface states can be realized.
-
\(8\pi\) Josephson spectrum \(\rightarrow\) parafermions!
- New realization avenues for parafermions in QD arrays are suggested.
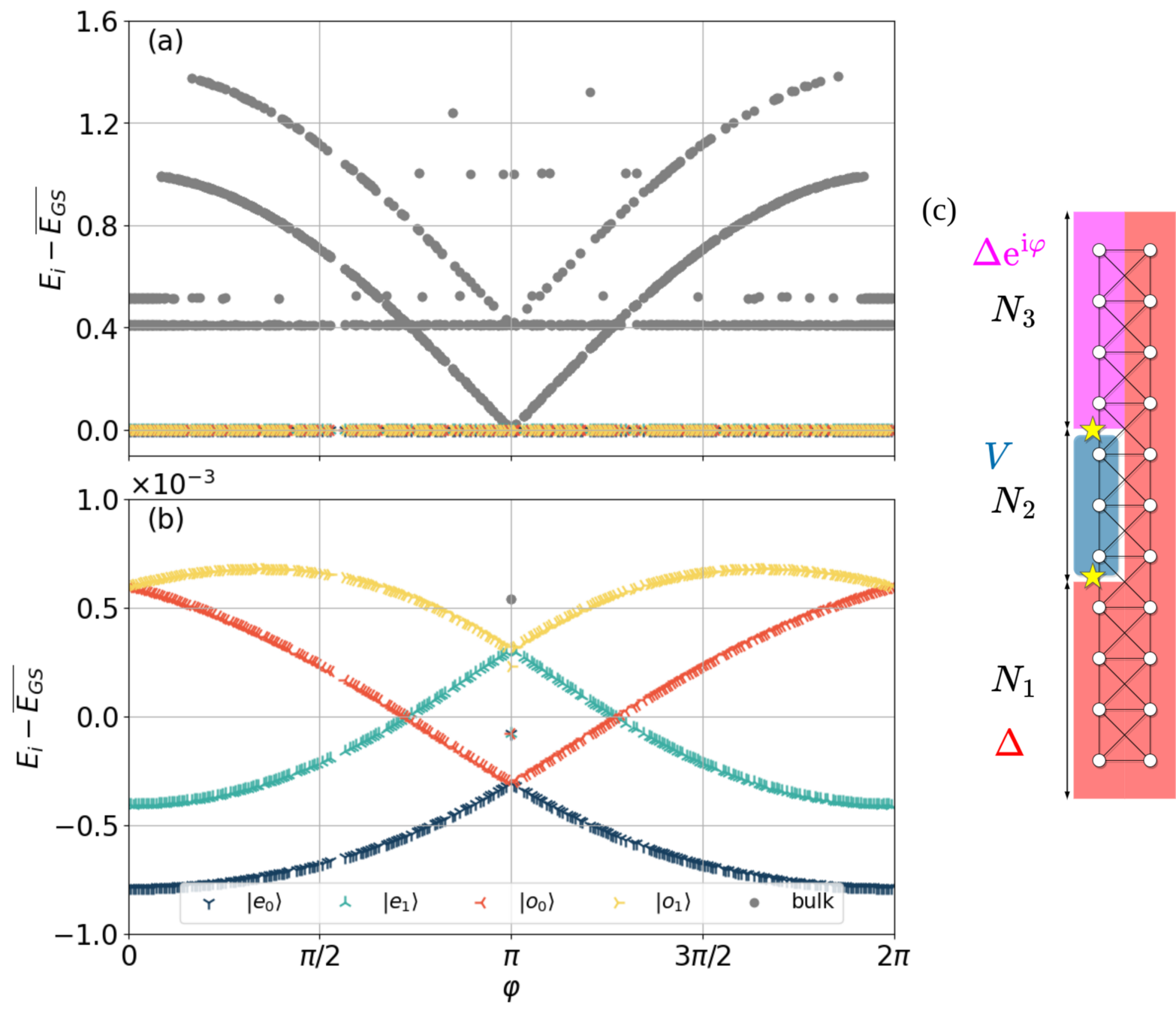
Josephson spectrum.. the details
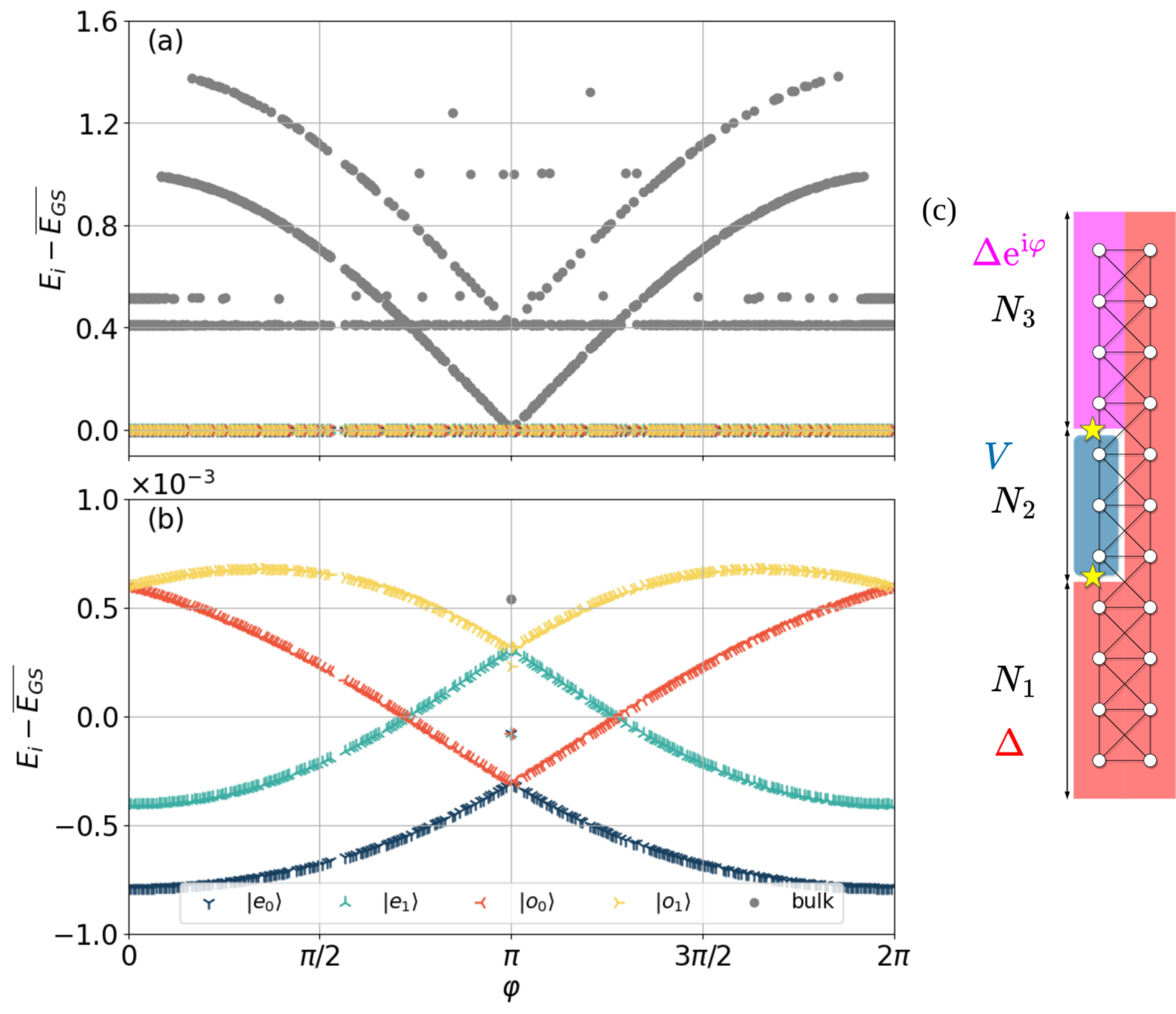
Josephson spectrum.. the details
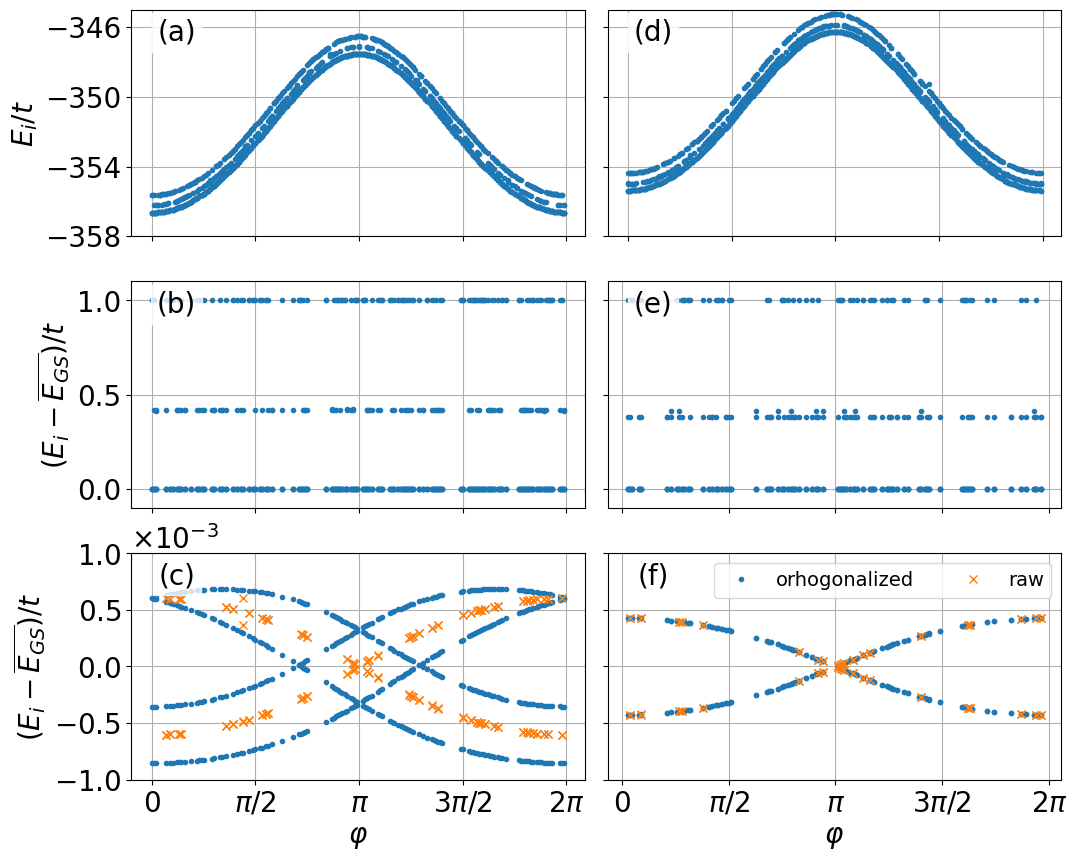
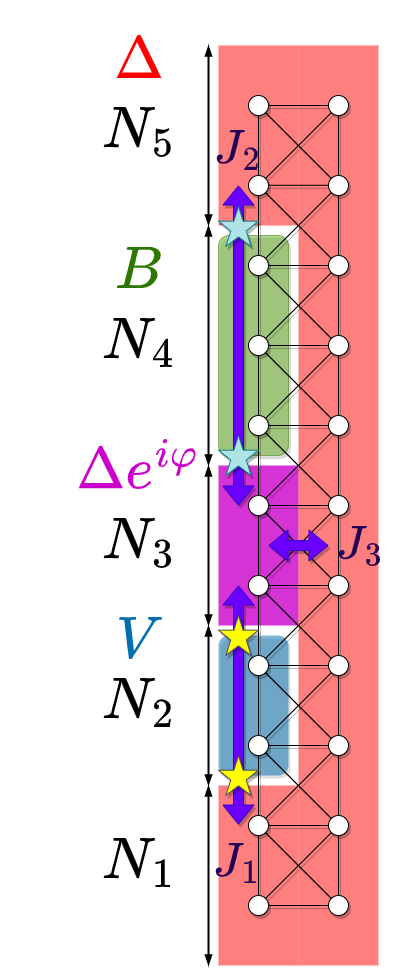
\( N_2<N_4<N_3 \)
\( N_4<N_2<N_3 \)
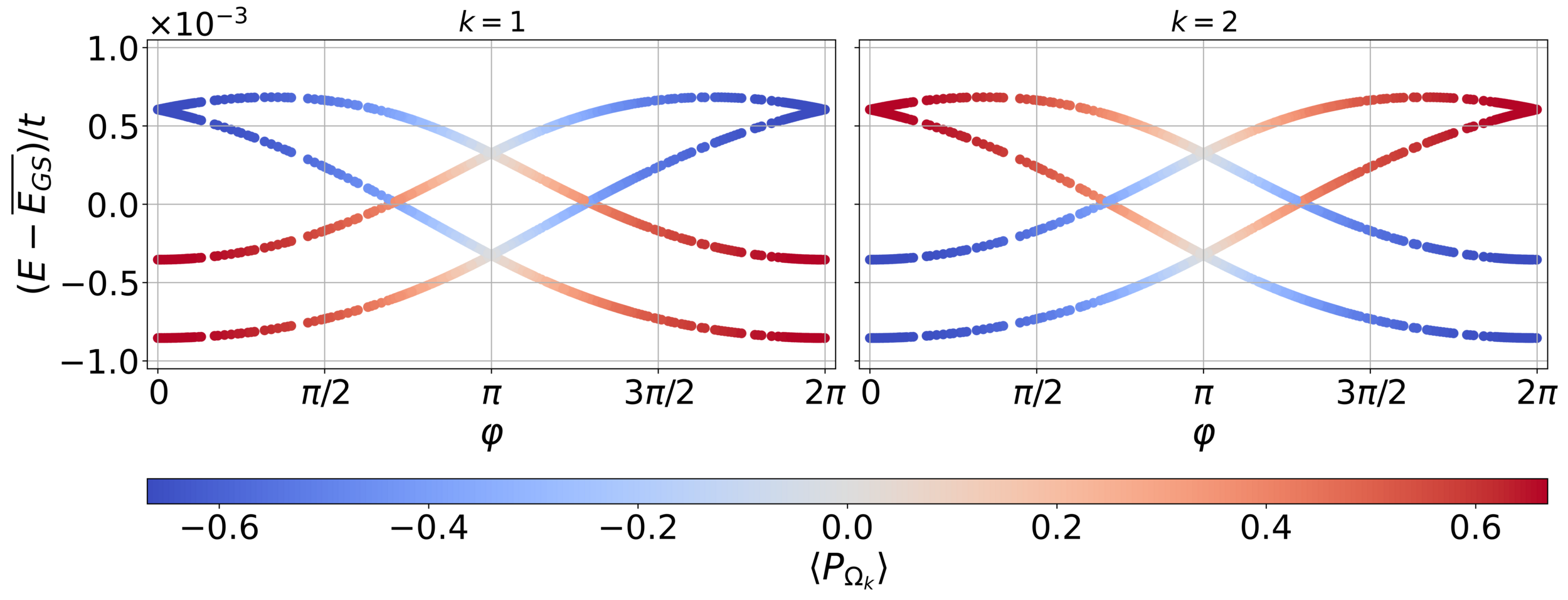
Local parity
P_\Omega=\prod_{p\in\Omega,\sigma}\left (-1\right )^{n_{p,\sigma}}
\Omega_1
\Omega_2
\(\mathbb{Z}_{4}\) parafermions from ordinary fermions
A. Calzona, T. Meng, M. Sassetti, T. L. Schmidt
Phys. Rev. B 98, 201110(R) (2018)
N=4 clock model/
parafermion chain
each site
has 4 states
spinful electron
in 1D wire
Hamiltonian in fermion language ...
\bar H (U,V) = H^{(2)} + U \left[ V \left(H^{(4)} + H^{(6)} \right) + (1-V) \bar H^{(4)}\right]
\displaystyle \bar H^{(4)} = -J \sum_{\sigma,j} \Big[c_{\sigma,j}^\dagger c_{\sigma, j+1} \left(-n_{-\sigma,j}-n_{-\sigma,j+1}\right) \\ + c_{\sigma,j}^\dagger c_{\sigma,j+1}^\dagger \left(n_{-\sigma,j}-n_{-\sigma,j+1}\right)\Big] +h.c.
\displaystyle
\begin{aligned}
H&=H^{(2)}+H^{(4)}+H^{(6)}\\
H^{(2)}&=- J \sum_{\sigma,j} \left[c_{\sigma,j}^\dagger c_{\sigma, j+1} -i \;c_{-\sigma,j}^\dagger c^\dagger_{\sigma,j+1} \right] +h.c.\,,\\
H^{(4)}&= -J\sum_{\sigma,j} \Big[ c_{\sigma,j}^\dagger c_{\sigma, j+1} \left(- n_{-\sigma,j}-n_{-\sigma,j+1}\right)\\
&+ c_{\sigma,j}^\dagger c_{-\sigma, j+1}\; i \left( n_{-\sigma,j} + n_{\sigma,j+1} \right) \\
&+ c_{-\sigma,j}^\dagger c^\dagger_{\sigma,j+1}\; i \left(n_{\sigma,j}+n_{-\sigma,j+1}\right) \\
&+ c_{\sigma,j}^\dagger c^\dagger_{\sigma,j+1} \left(n_{-\sigma,j}-n_{-\sigma,j+1}\right)\Big] + h.c.\,, \\
H^{(6)}&= - J \sum_j \Big[ - 2 i\, c_{\sigma,j}^\dagger c_{-\sigma, j+1} \left( n_{-\sigma,j} n_{\sigma,j+1}\right) \\
\qquad \qquad &- 2i \, c_{-\sigma,j}^\dagger c^\dagger_{\sigma,j+1} \left(n_{\sigma,j} n_{-\sigma,j+1}\right) \Big] +h.c.
\end{aligned}
... is complicated with 3 body interactions encoded in the \(H^{(6)}\) term
Threading a flux and Josephson
\displaystyle H_0=\sum_{m=1}^{L-1}\sigma_m^\dagger\sigma_{m+1} + \mathrm{h.c.}, \quad
H=H_0+C e^{i\varphi}+C^\dagger e^{-i\varphi}
\displaystyle Q=\prod_m \tau_m
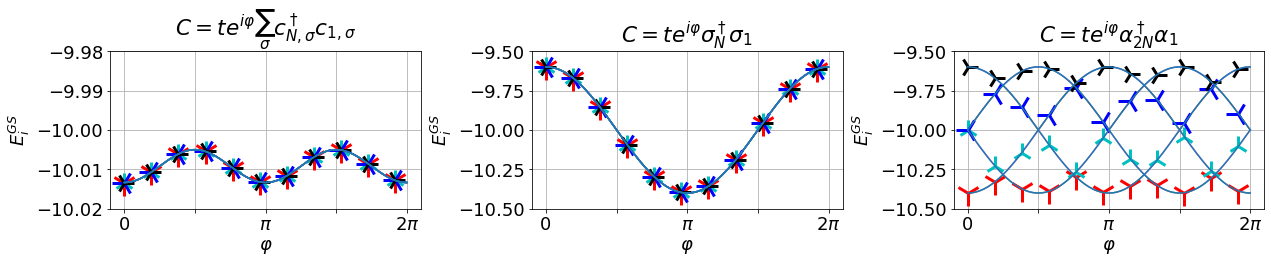
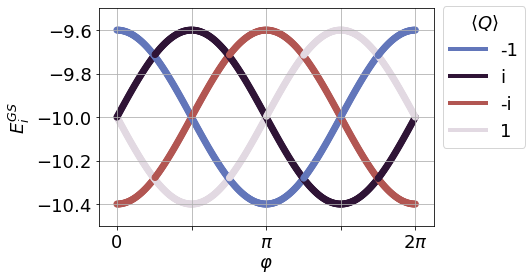
parafermion charge
threading a flux method depends on the coupling...
Parafermions in a simple electronic ladder
By László Oroszlány
