Graphene triangulenes embedded in hexagonal
boron nitride
Eötvös Loránd University
Dániel Pozsár
László Oroszlány, Viktor Ivády



The Team



- László Oroszlány, Zoltán Tajkov, János Koltai, Dániel Pozsár, Andor Kormányos, András Balogh, Tamás Véber, Marcell Sipos
- Jaime Ferrer, Amador Garcia Fuente, Gabriel Martinez-Carracedo, Aurelio Hierro Rodriguez, Balázs Nagyfalusi, Rosa Eulalia González Ferreras
- Felix Büttner, Kai Litzius, Steffen Wittrock
- Efren Navarro-Moratalla, Marta Galbiati, Jose Joaquin Perez Grau
- László Szunyogh, László Udvardi, Bendegúz Nyári, Anjali Jyothi Bhasu




























Antiferromagnetic spin-1 chains
- Haldane gap
-
BLBQ nearest neighbor model
- Measurement based quantum computing
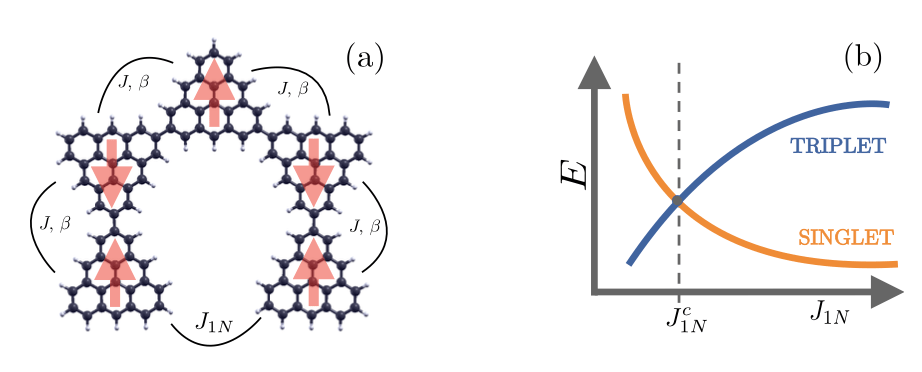
Martínez-Carracedo, Gabriel, et al. "Electrically driven singlet-triplet transition in triangulene spin-1 chains." Physical Review B 107.3 (2023): 035432.
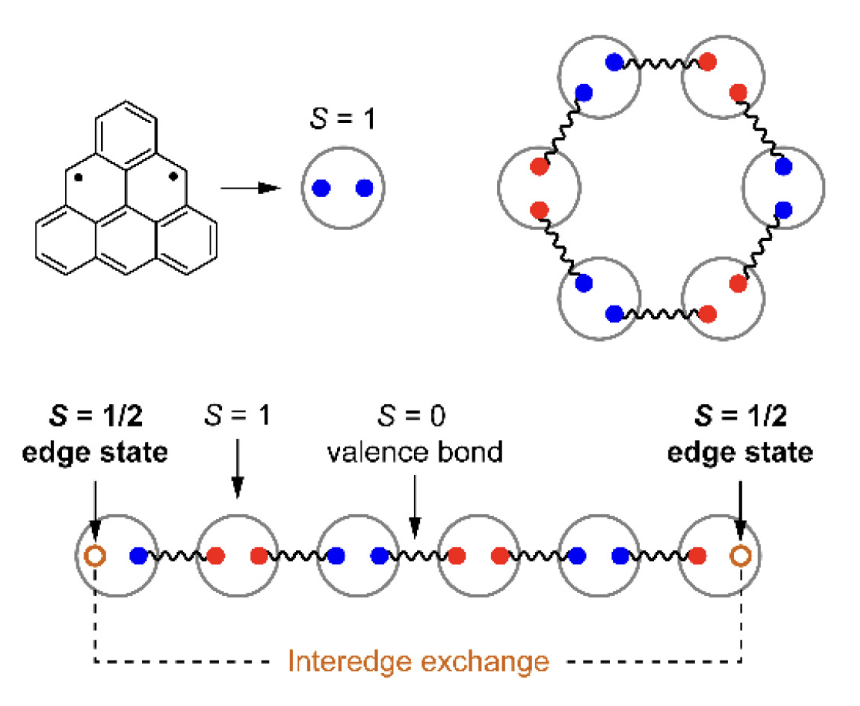
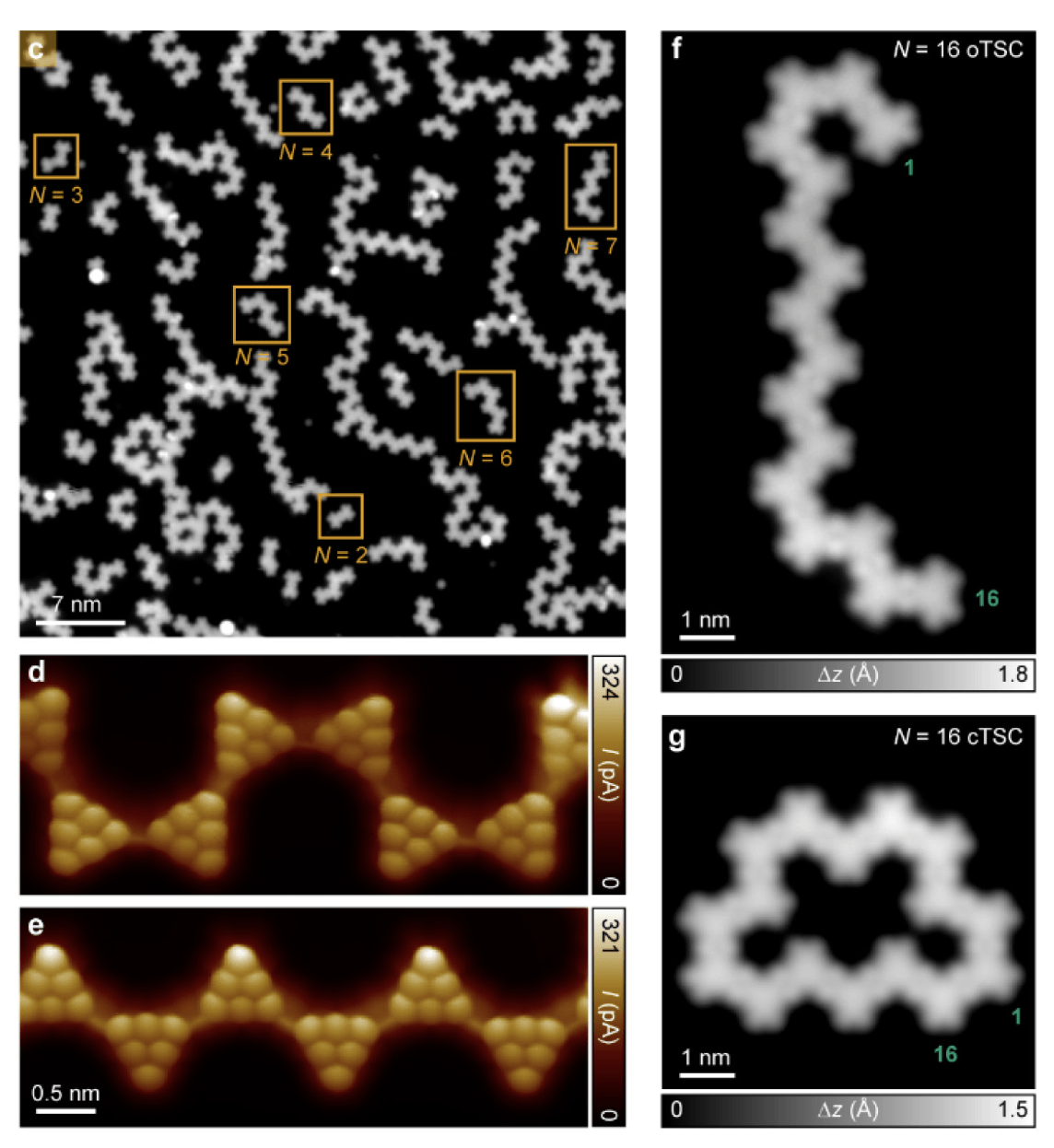
Mishra, Shantanu, et al. "Observation of fractional edge excitations in nanographene spin chains." Nature 598.7880 (2021): 287-292.
Determination of ground state spin in triangulenes

Angew. Chem. Int. Ed. 10.1002/anie.23783
- Lieb's theorem for bipartite lattices
- Ovchinnikov's rule
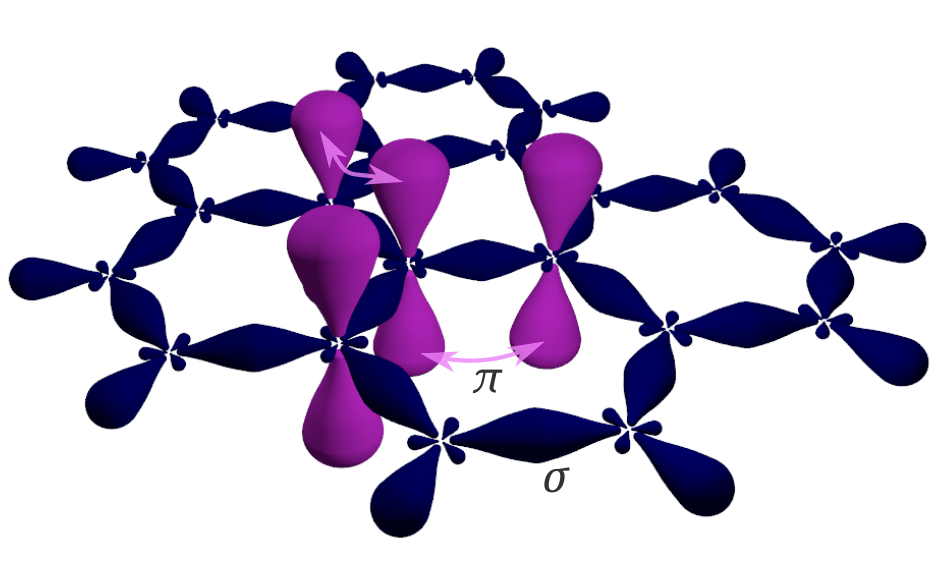
Embedding in hexagonal boron nitride
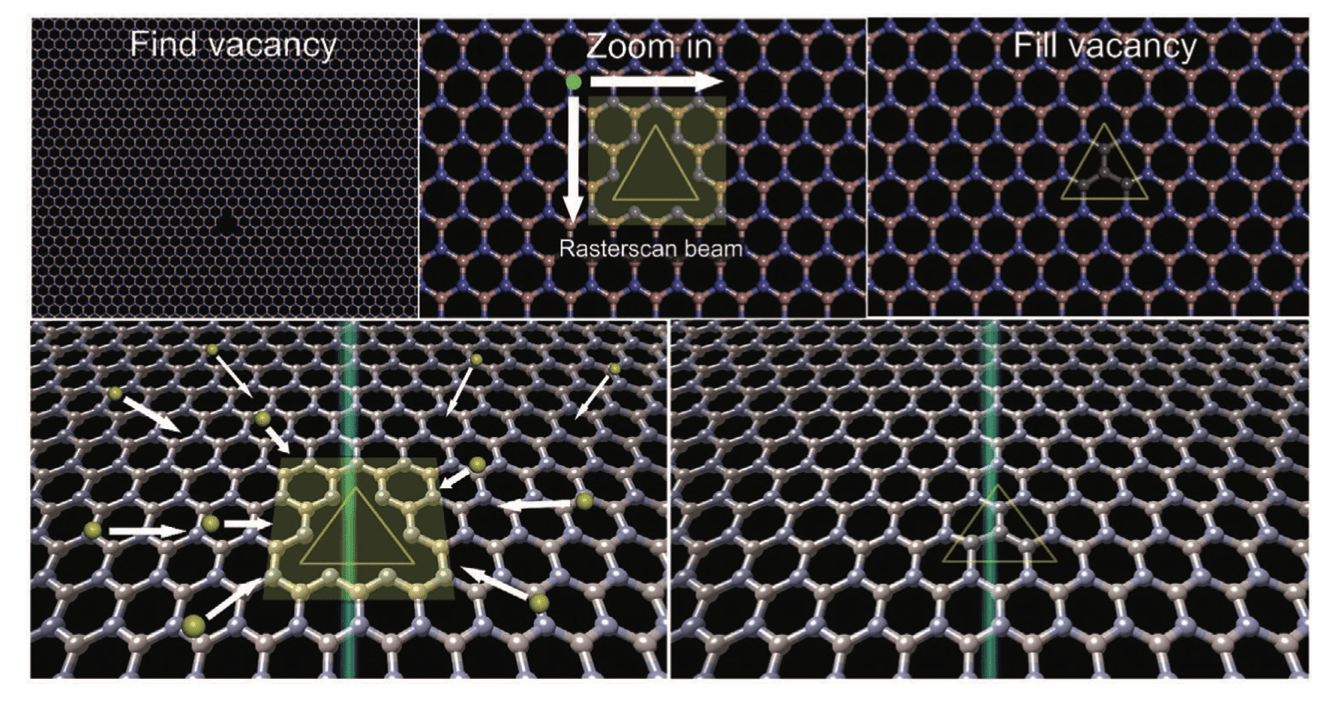
Park, Hyoju, et al. "Atomically precise control of carbon insertion into hBN monolayer point vacancies using a focused electron beam guide." Small 17.23 (2021): 2100693.
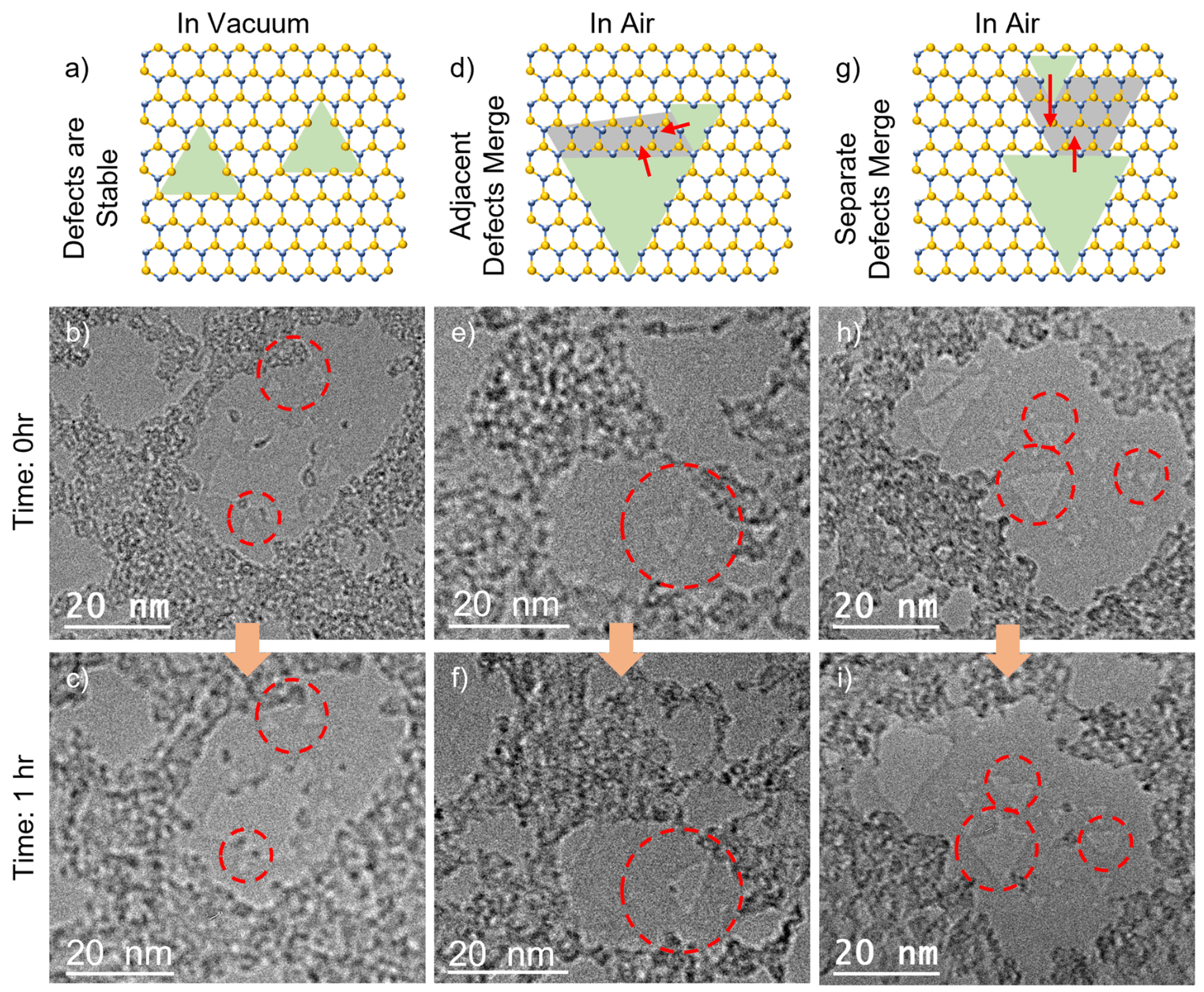
Dai, Chunhui, et al. "Evolution of nanopores in hexagonal boron nitride." Communications chemistry 6.1 (2023): 108.

DFT perturbation theory
|
Oroszlány, László, et al. "Exchange interactions from a nonorthogonal basis set: From bulk ferromagnets to the magnetism in low-dimensional graphene systems." Physical Review B 99.22 (2019): 224412. |
Perturbation of classical Hamiltonian
Energy of infinitesimal rotations from Kohn-Sham Hamiltonian
Collinear DFT:
LKAG and magnetic force theorem:
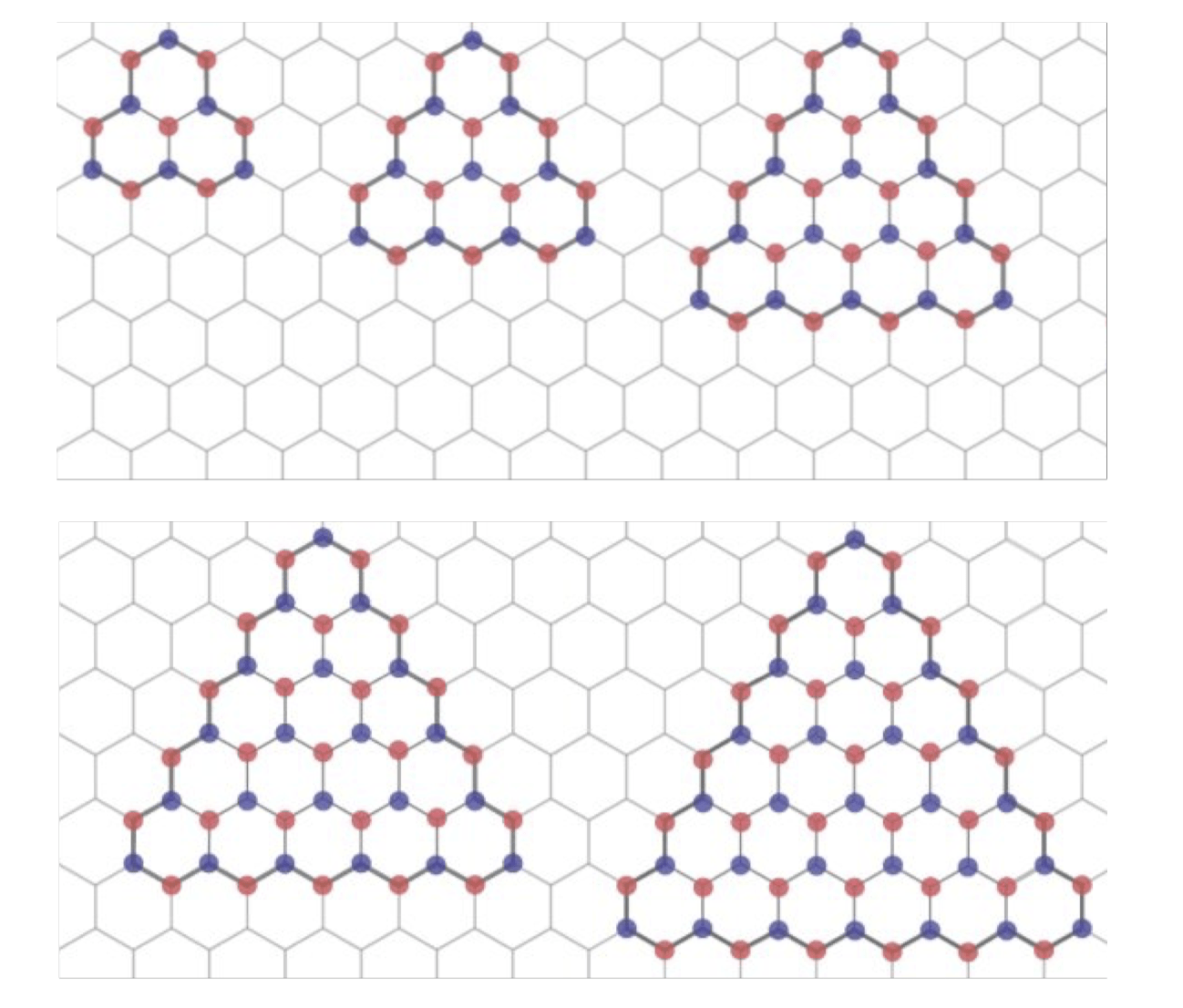
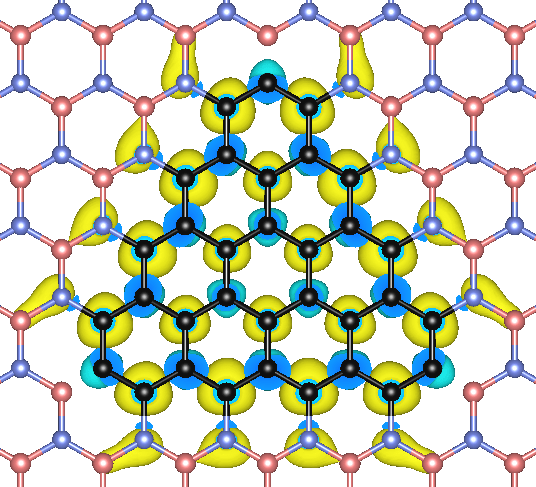
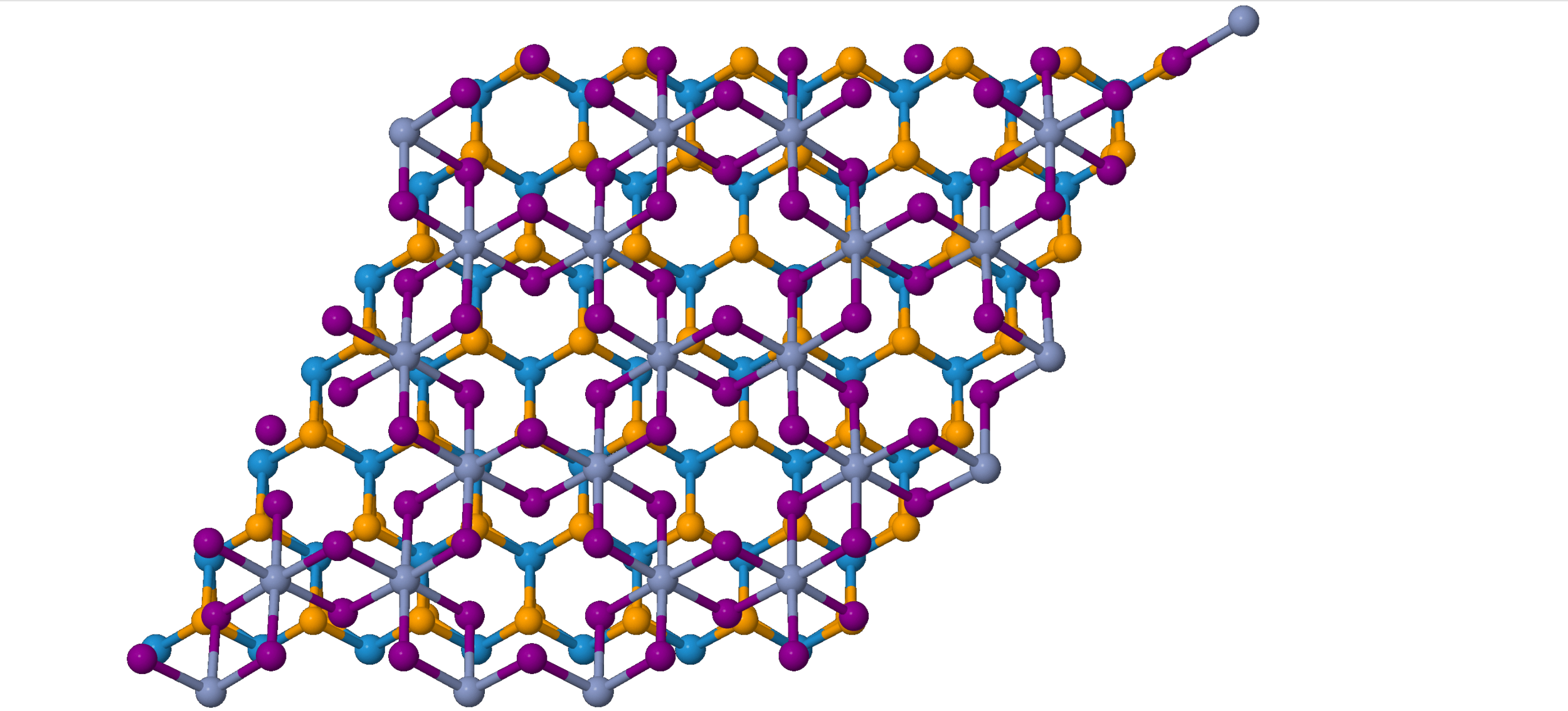
Result of the embedding process
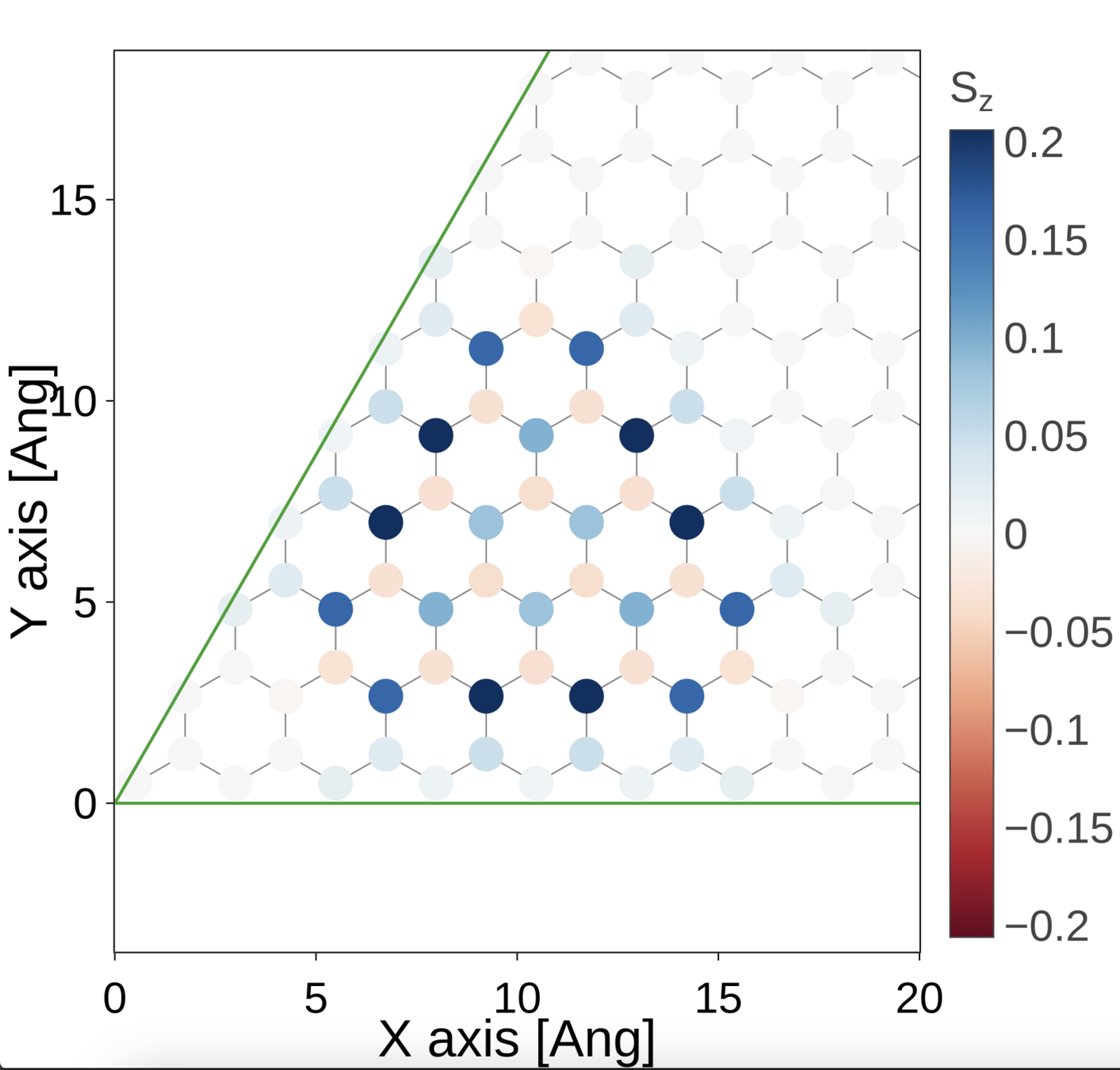
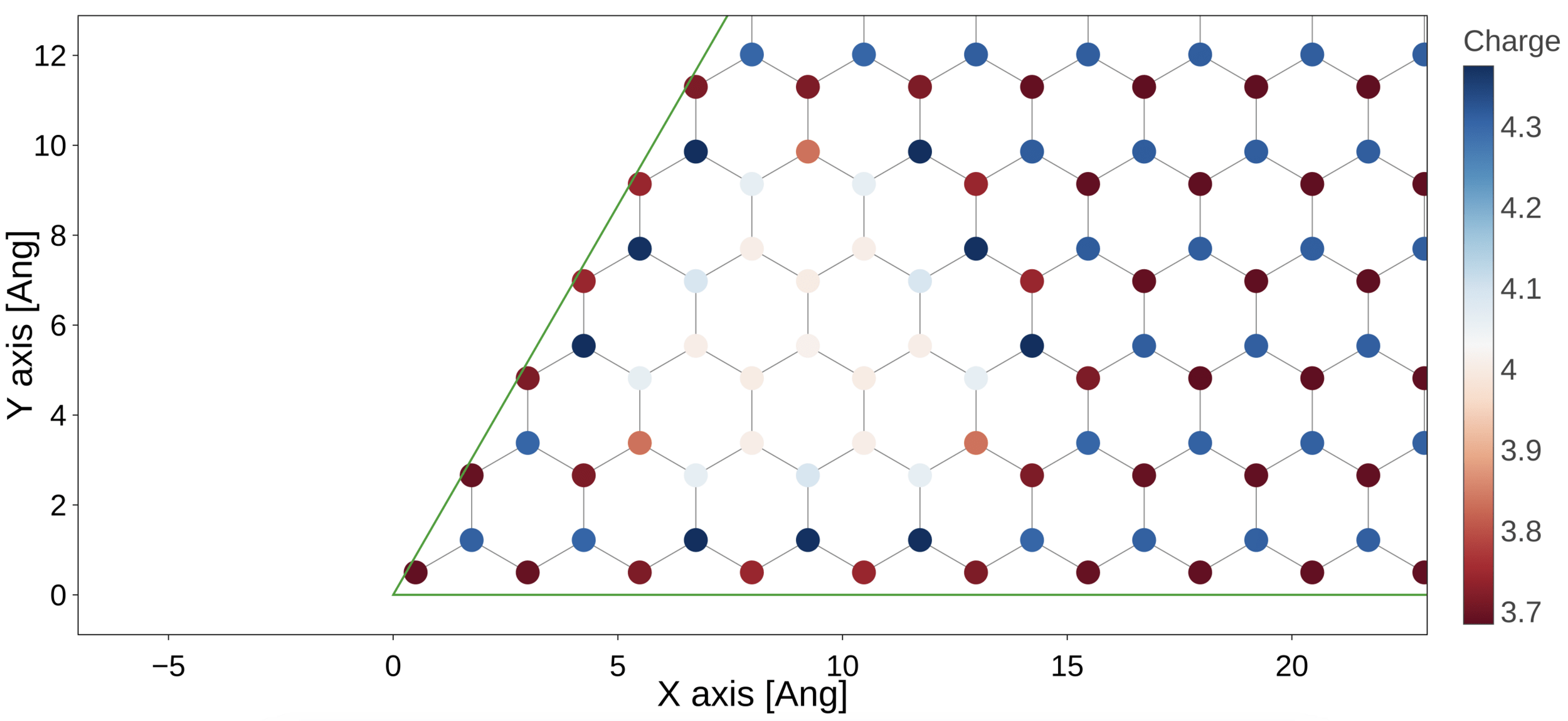
Result of the embedding process

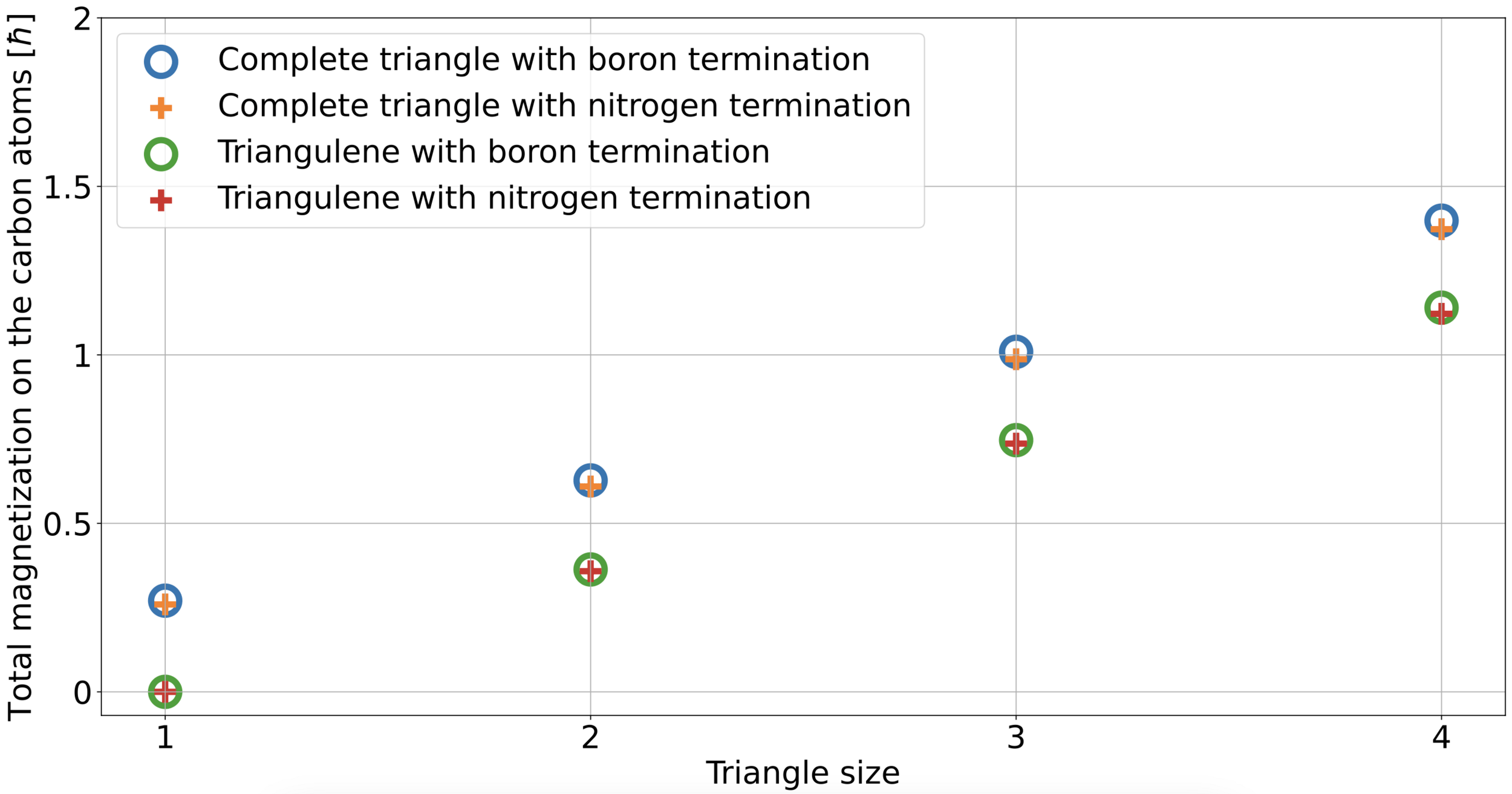
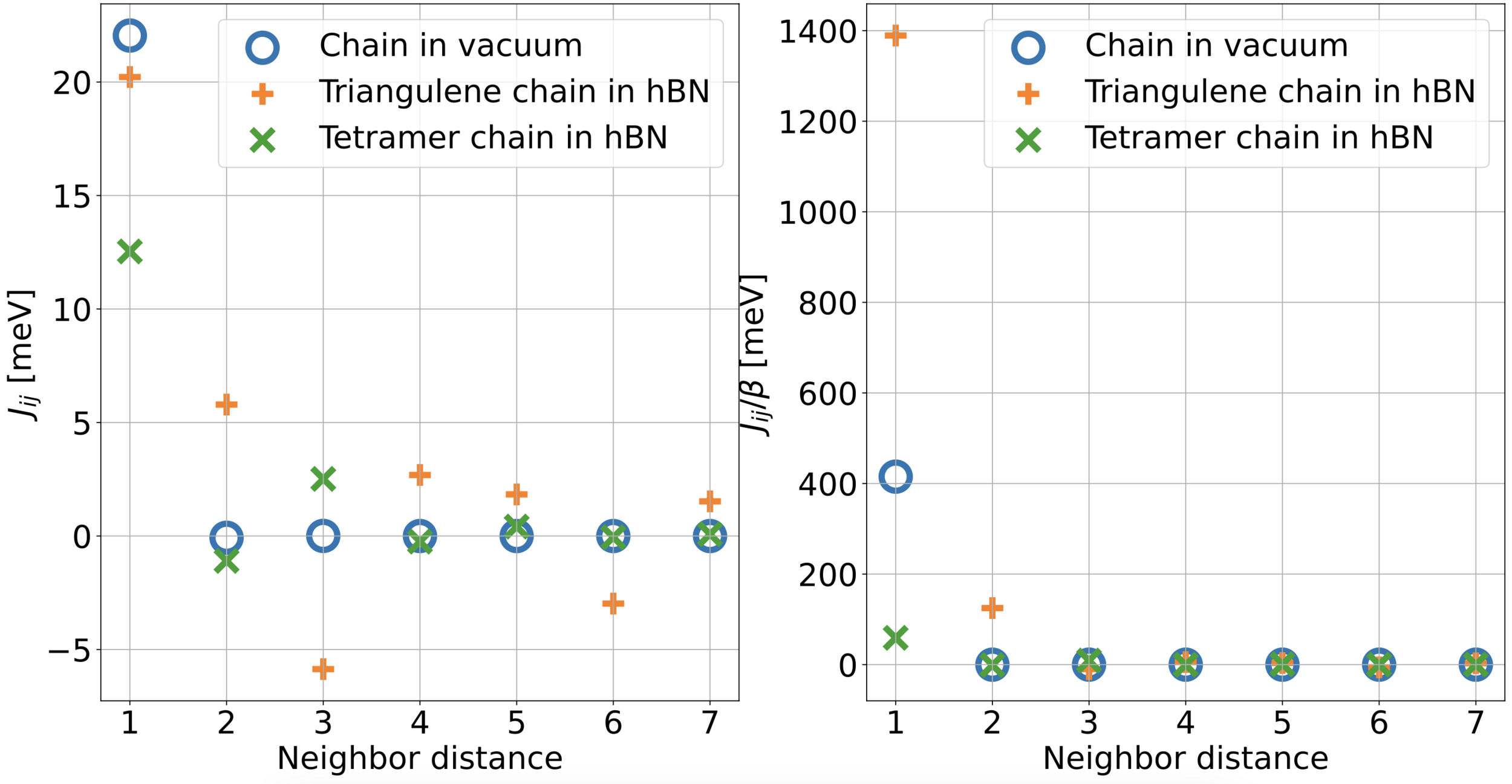
Modelling infinite chains
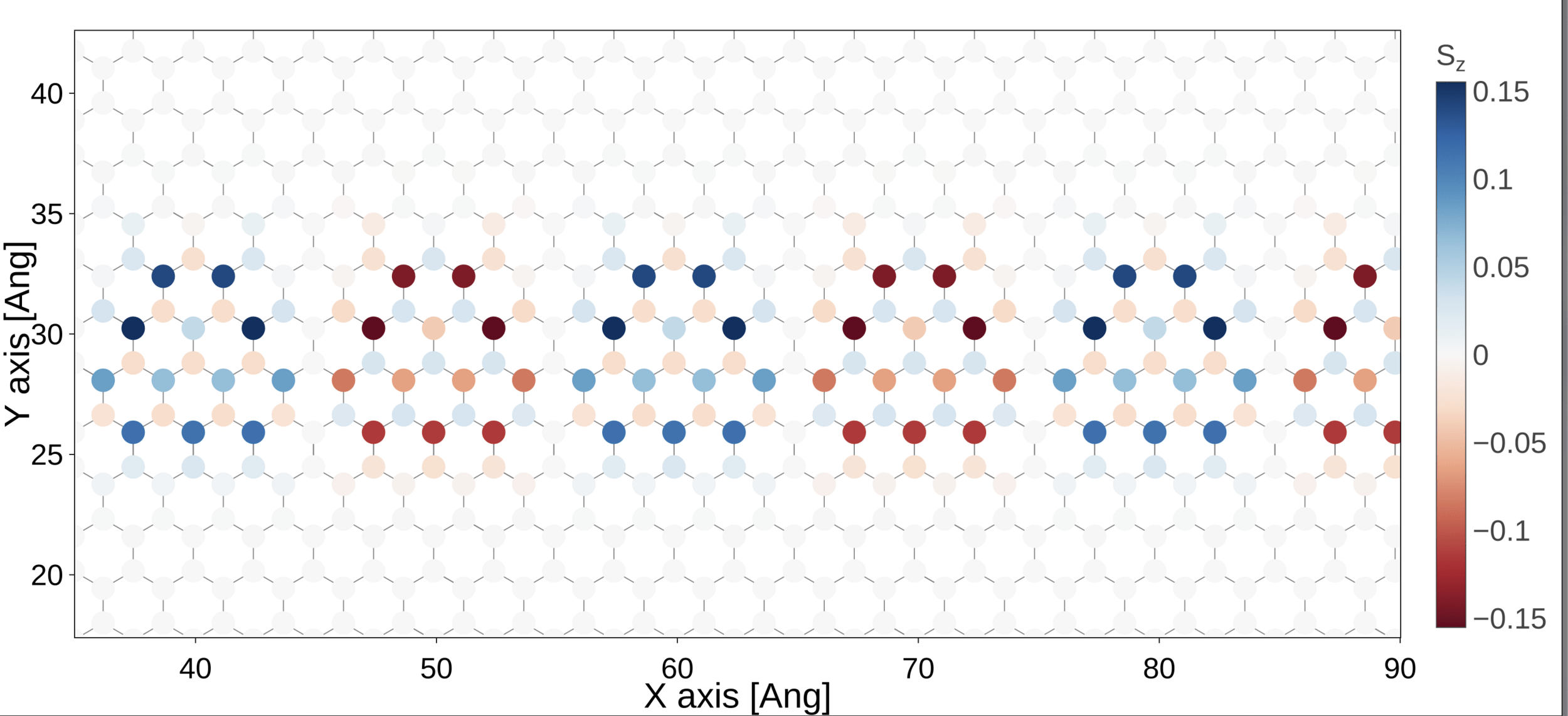

| Experiment | Triangulene in hBN | Triangulene in vacuum | |
|---|---|---|---|
| 18 meV | 20.22 meV | 19.75 meV | |
| 0.09 | 0.01 | 0.05 |
Mishra, Shantanu, et al. "Observation of fractional edge excitations in nanographene spin chains." Nature 598.7880 (2021): 287-292.

Relativistic magnetic interactions
- Very early release !!
- https://github.com/danielpozsar/grogu
- Single DFT calculation
- Pair creation is extremely cheap
- parallel BZ integral with MPI or CUDA
- Generalised Heisenberg model

UNDER 1 Hour on 8 GPUs
Copy of DPG presentation
By László Oroszlány
Copy of DPG presentation
- 148



