Towards measurement based quantum computation with multipods
Claire Benjamin1,2, Dániel Varjas3,4, Gábor Széchenyi5,6, Judit Romhányi1, László Oroszlány2,6
1Department of Physics and Astronomy, University of California, Irvine;
2Department of Physics of Complex Systems, Eötvös Loránd University;
3Department of Theoretical Physics, Institute of Physics, Budapest University of Technology and Economics;
4Institute for Theoretical Solid State Physics, IFW Dresden and Würzburg-Dresden Cluster of Excellence;
5Department of Materials Physics, Eötvös Loránd University;
6HUN-REN Wigner Research Centre for Physics
The Team
Dániel Varjas
BME & IFW
Gábor Széchenyi
ELTE & Wigner FK
Judit Romhányi
UC Irvine
Claire Benjamin
UC Irvine
Measurement based quantum computing
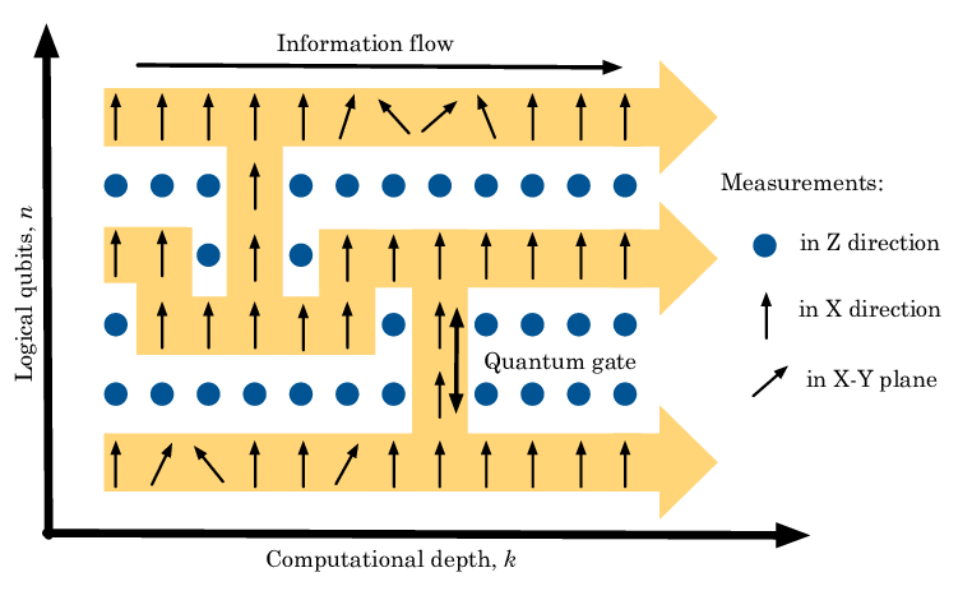
Raussendorf, Briegel Phys. Rev. Lett. 86, 5188 (2001)
Raussendorf
Looking for resource states
Wei, Affleck, Raussendorf Phys. Rev. Lett. 106, 070501 (2011)
Tzu-Chieh Wei
Ian Affleck
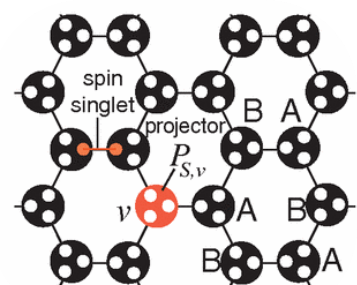
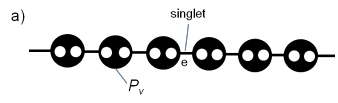
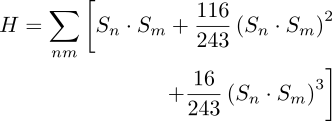
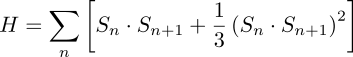
Looking for higher spins
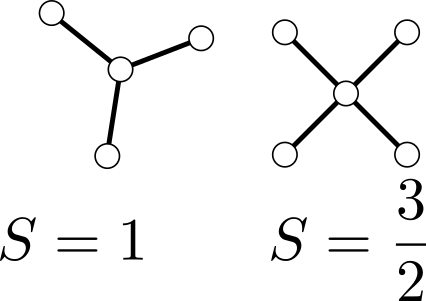
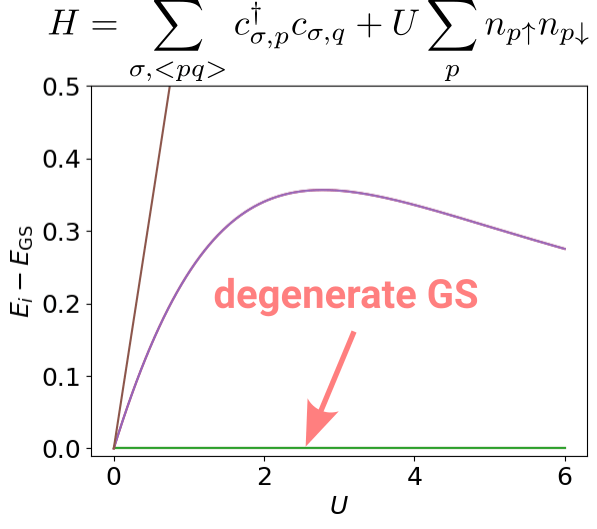
Lieb Phys. Rev. Lett. 62, 1927 (1989)
Elliott Lieb
Stars are quite resilient!
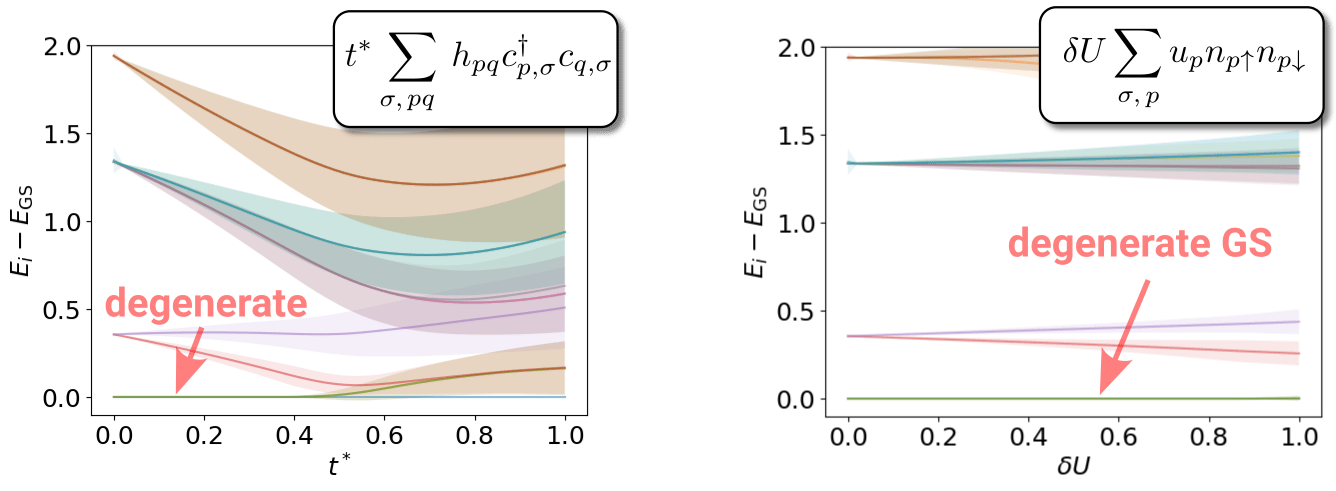
S=1 AKLT: How to couple two stars?
t_{l1}
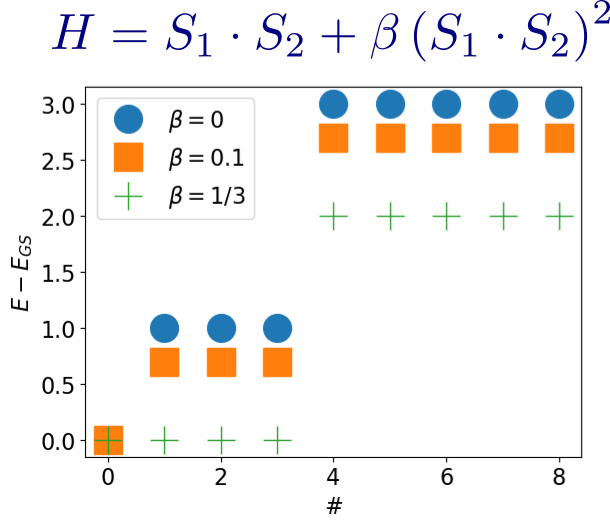
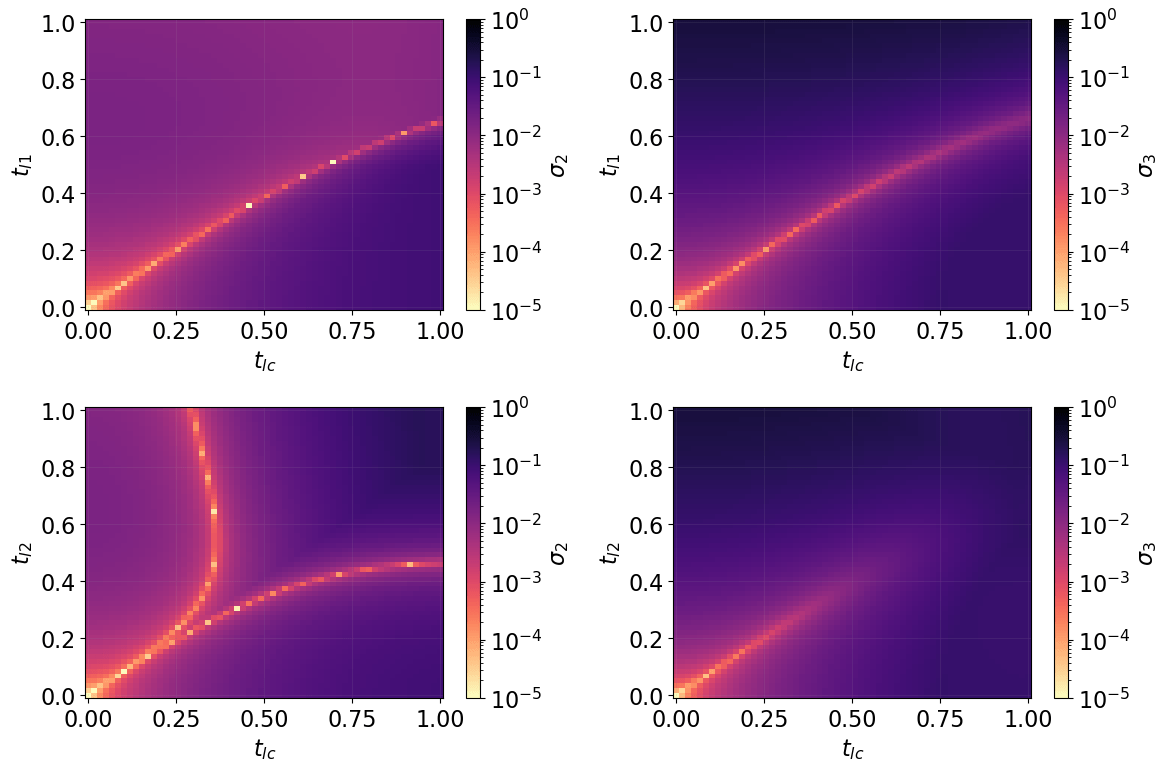
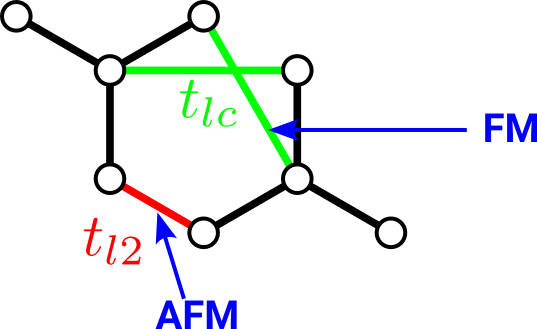
Effective model for spins from QDPT!
Day, et al. Phys. Codebases 50 (2025)
pymablock.readthedocs.io
H_0 + p H_1 \Rightarrow \tilde{H}_0+\sum_n p^n \tilde{H}^{(n)}_1
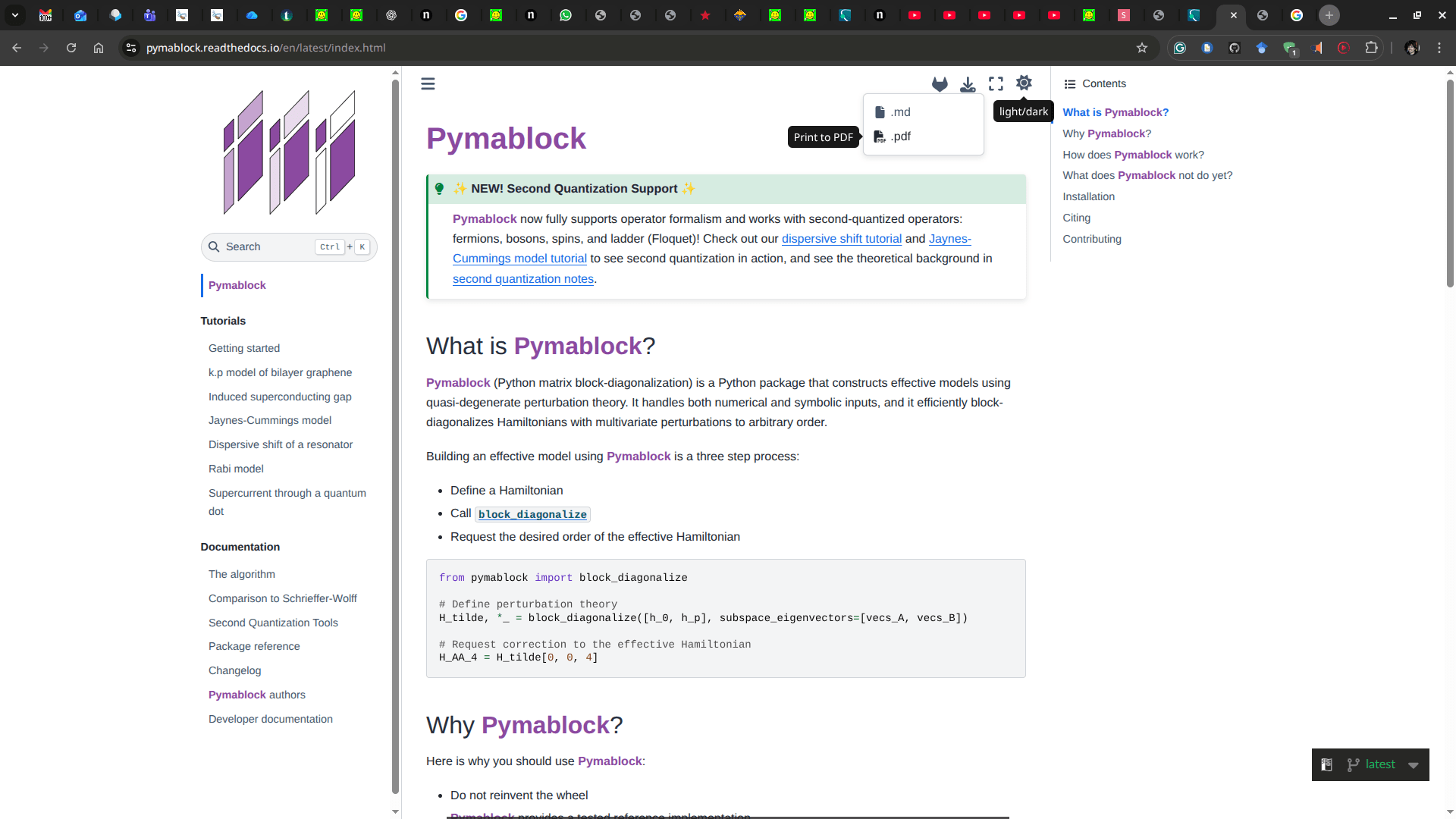
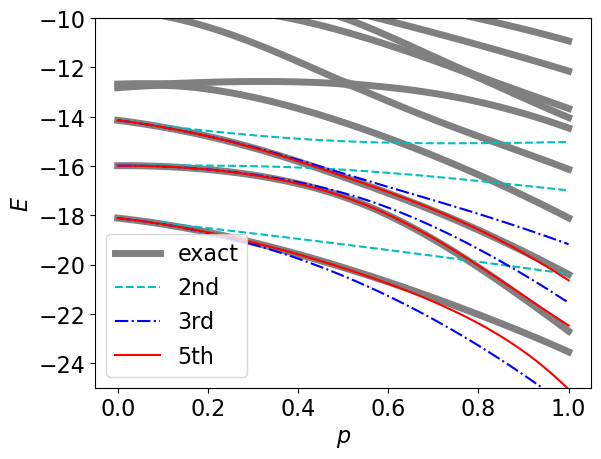
S=1 AKLT: How to couple two stars, PT
\underbrace{H_0 + p H_1}_{c_{n\sigma}} \Rightarrow \underbrace{\tilde{H}_0+\sum_n p^n \tilde{H}^{(n)}_1}_{S_i}
\left(S_i S_j\right)^n=a_nI+b_n\left(S_i S_j\right)+c_n\left(S_i S_j\right)^2
\tilde{H}=A(t)I+f(t)\left(S_1 S_2\right)+g(t)\left(S_1 S_2\right)^2
f(t^*)=3g(t^*)
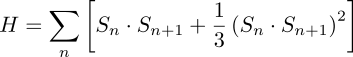
S=1 AKLT: How to couple many stars?
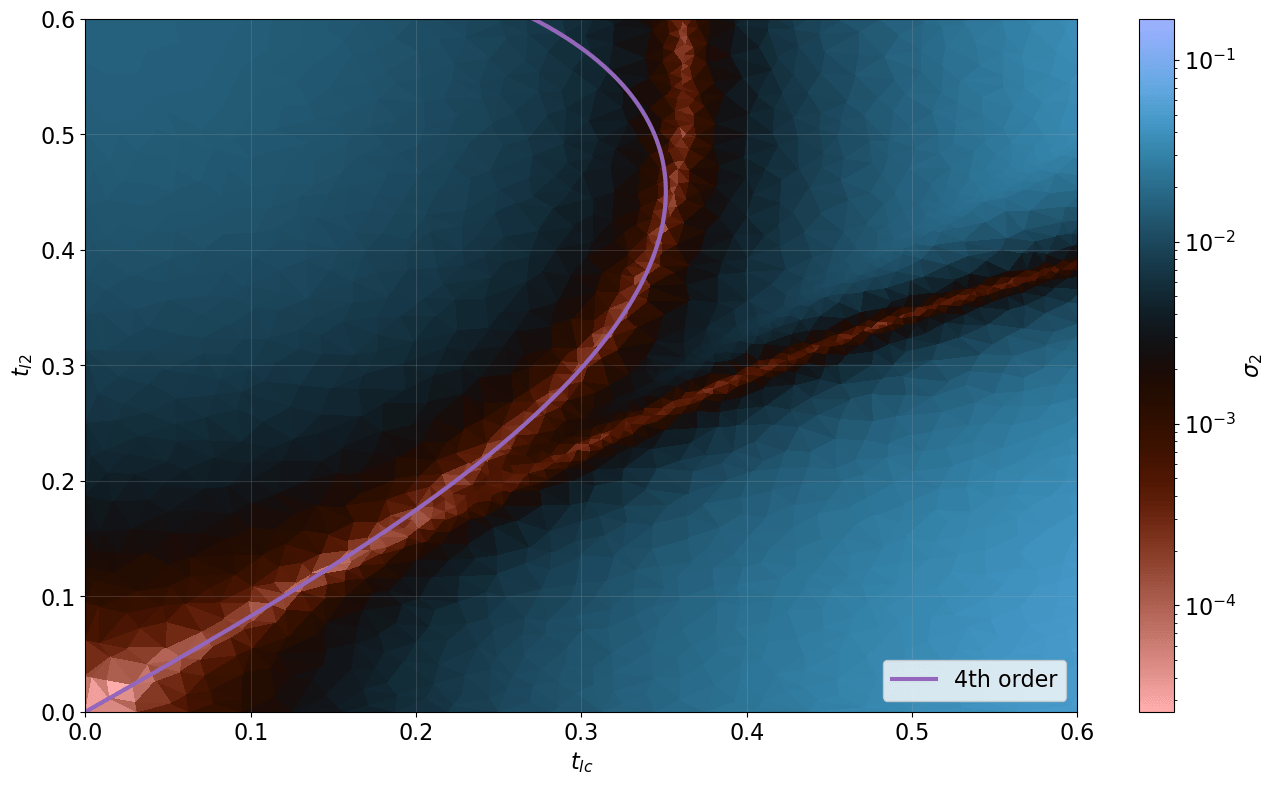
This is
promising!
S=3/2 AKLT: How to couple two stars?
H=\sum_{nm}\left[\left(S_1 S_2\right)+\frac{116}{243}\left(S_1 S_2\right)^2+\frac{16}{243}\left(S_1 S_2\right)^3\right]
f(t^*)=243/116g(t^*),\, f(t^*)=243/16h(t^*)
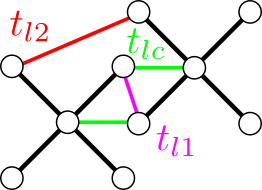
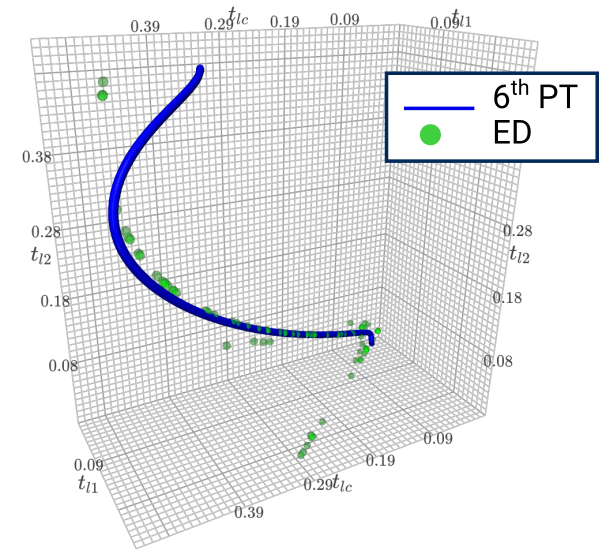
What about measurment?
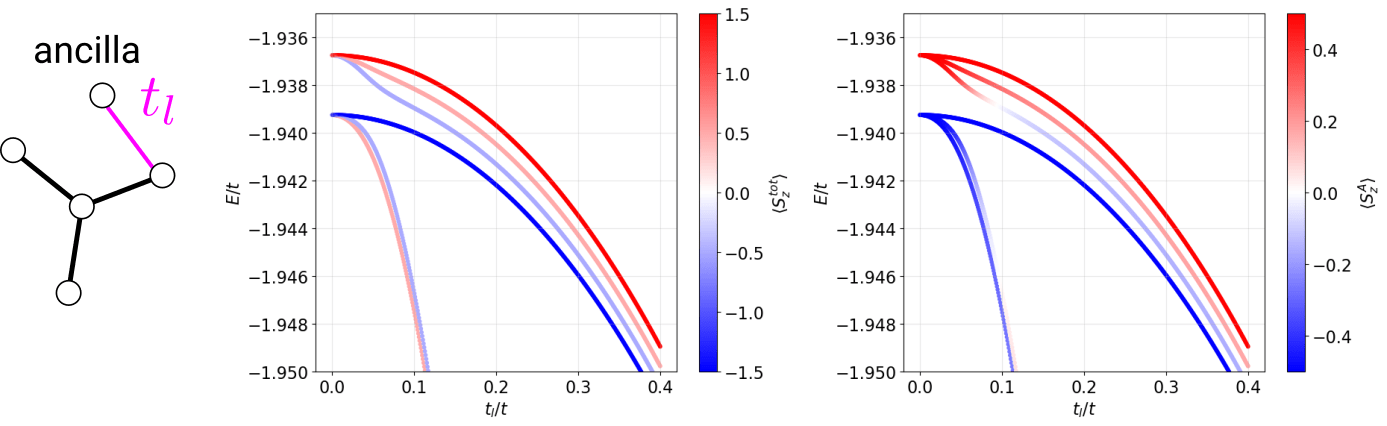
Experimental realization
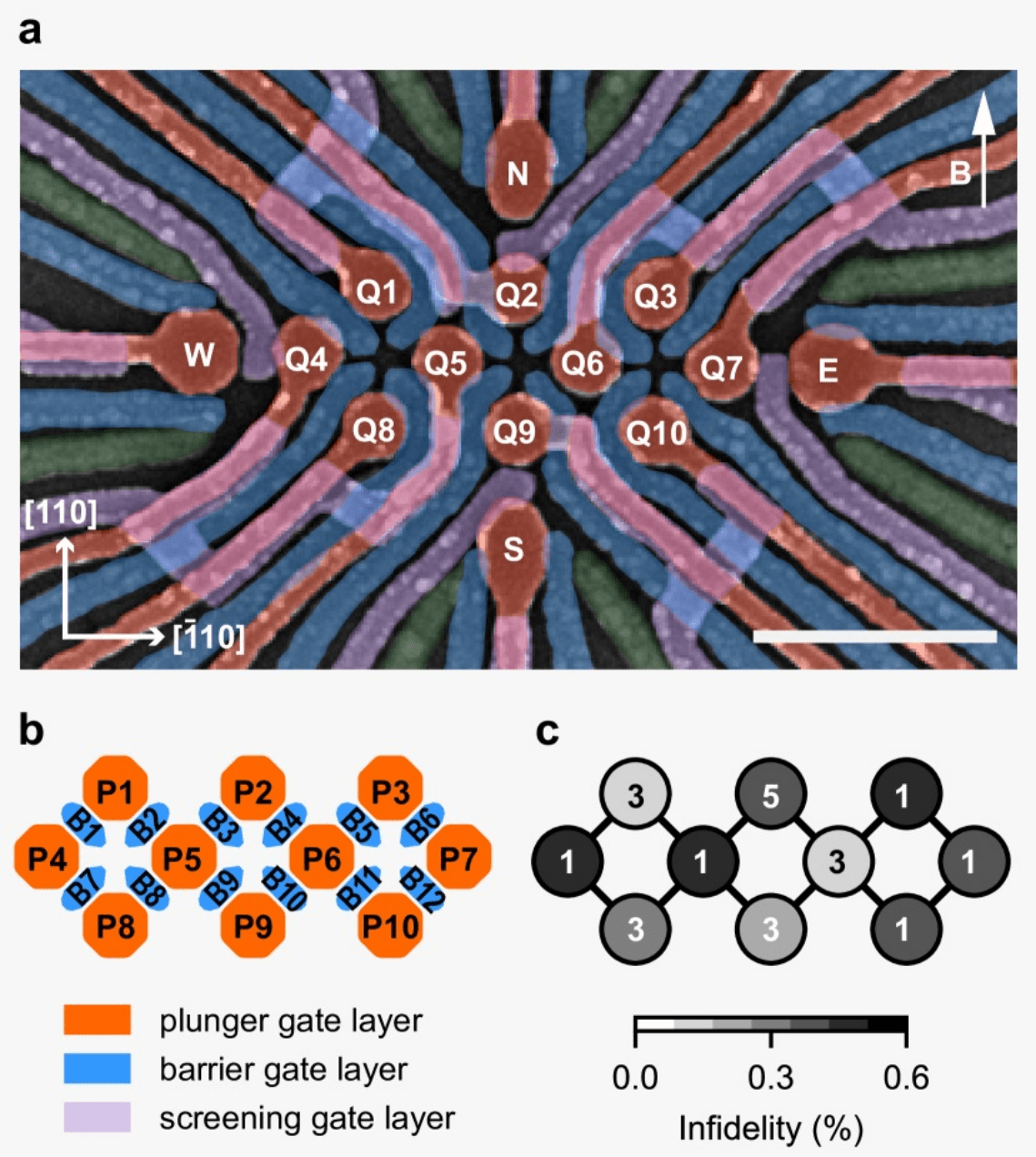
V. John et al. arXiv:2412.16044
multipods
By László Oroszlány
