Competition of trivial and topological phases in graphene based hybrid systems
László Oroszlány
Department of Physics of Complex Systems, Eötvös Loránd University
and MTA-BME Lendület Topology and Correlation Research Group









Duncan and Kekulé
Duncan, Charlie, Gene and Kekulé
Strained relationship


A colourful mess!
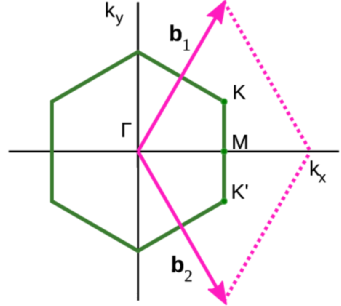
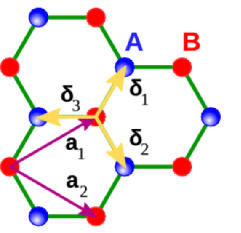
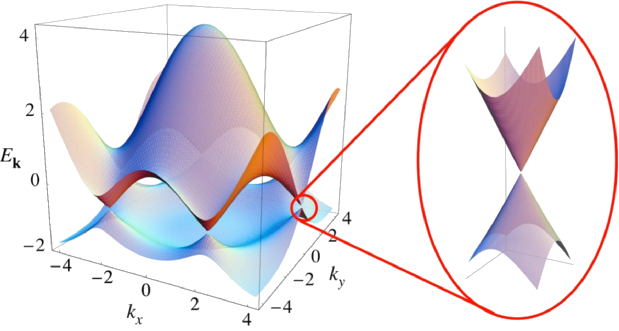
Graphene is ...
... a good template!
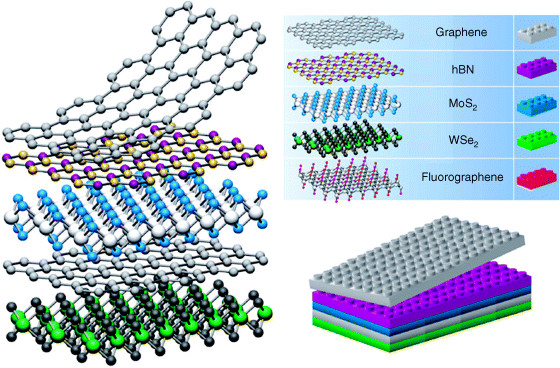
A. K. Geim, I. V. Grigorieva Nature 499, 419 (2013)
BiTeX: gigant SOC
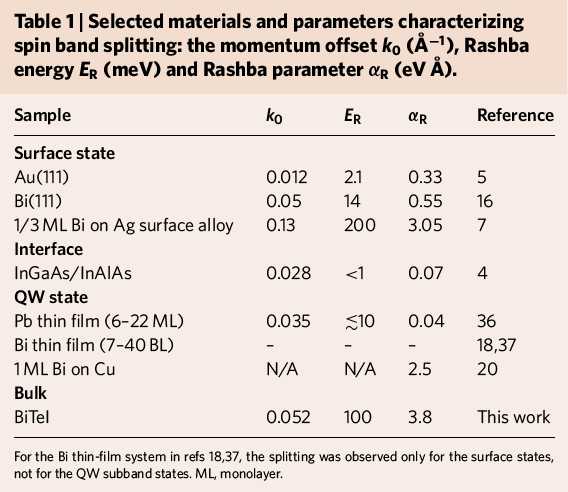
Ishizaka et al. Nature Materials 10, 521 (2011)
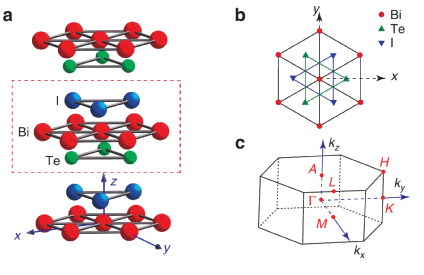
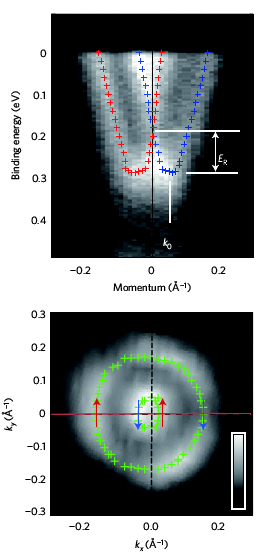
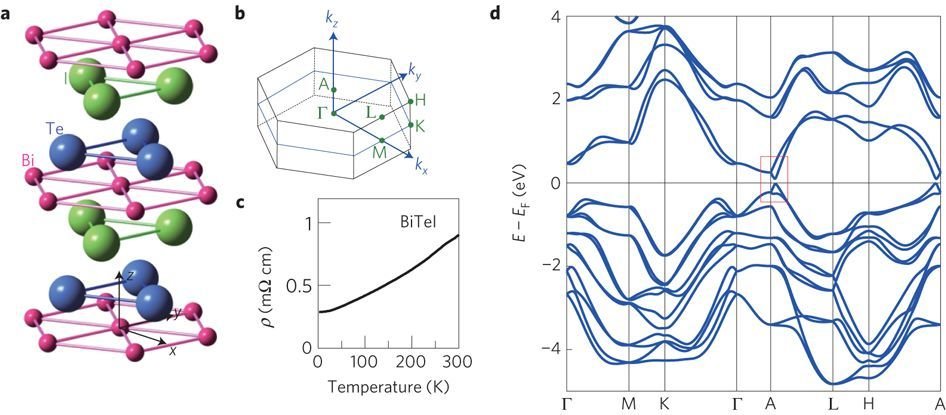
BiTeX monolayer
Fülöp et al. 2D Mater. 5, 031013 (2018)

BiTeX/graphene heterostructures
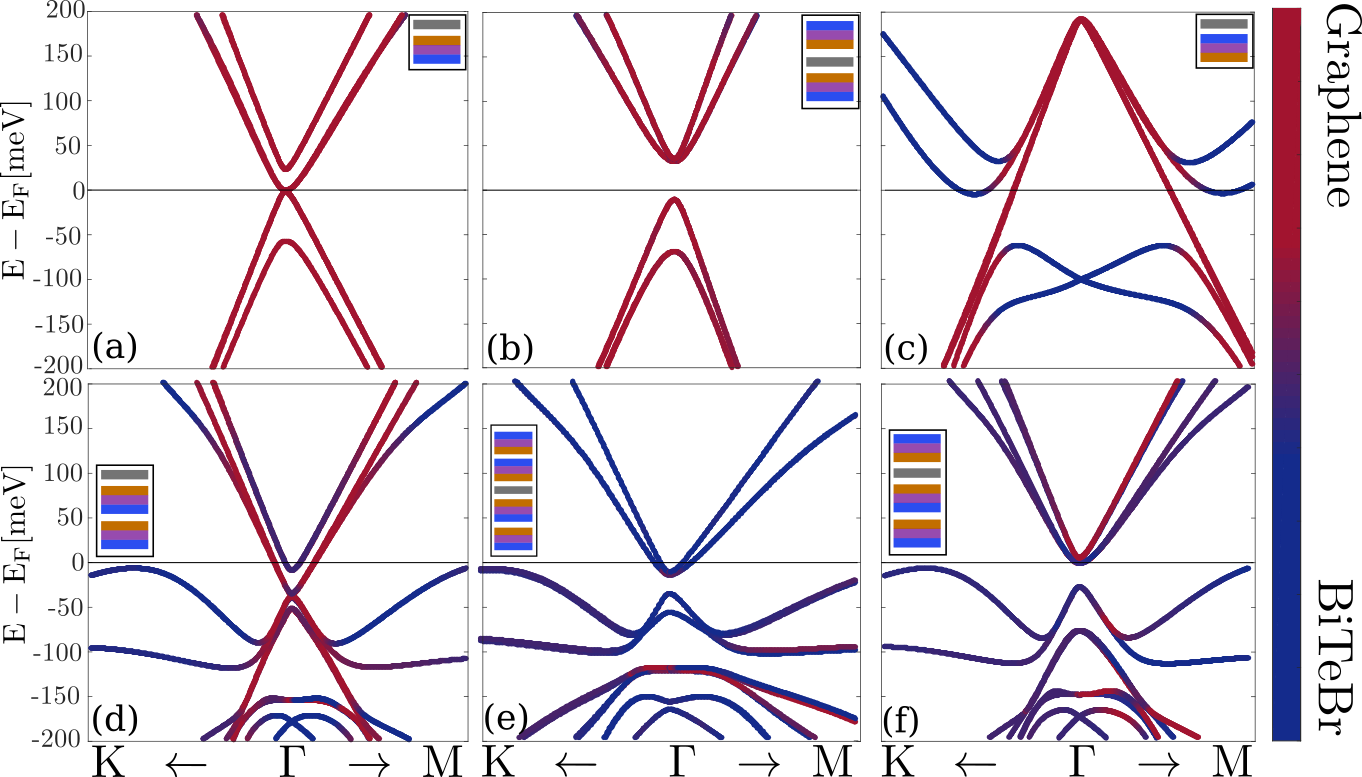

BiTeI sandwich: Kou et al. ACS Nano, 8 10448 (2014)
trivial
topological
Z. Tajkov el al. Nanoscale 11, 12704 (2019)
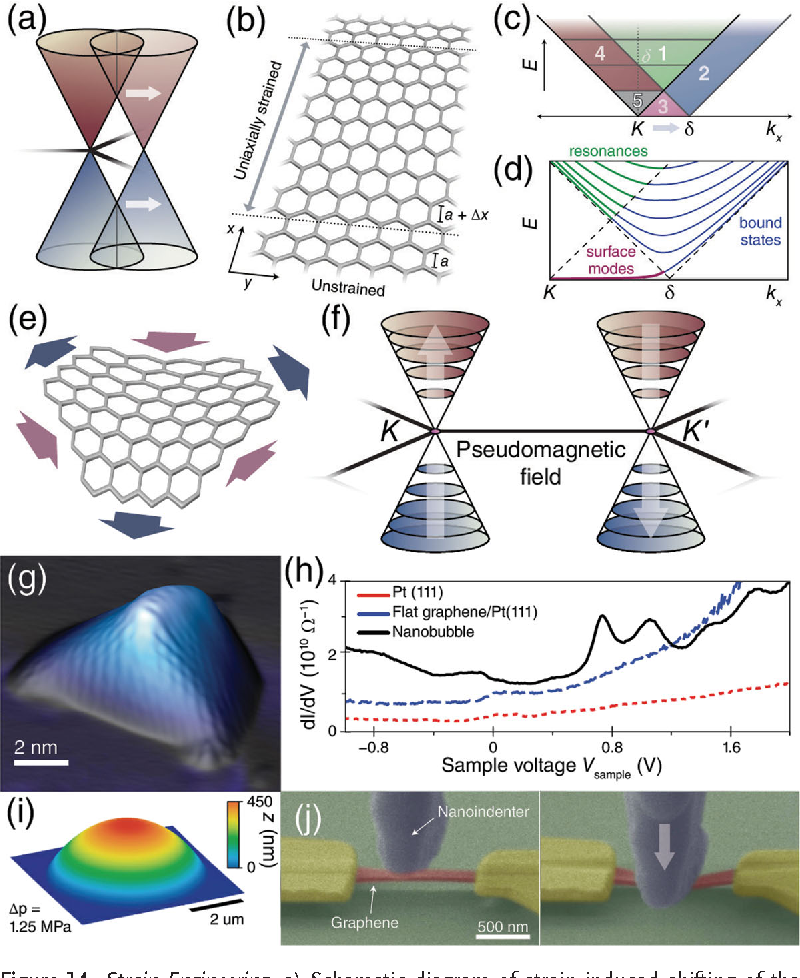



Mechanical distortions
in graphene
Weiss et al. Advanced Materials, 24 5782(2012)
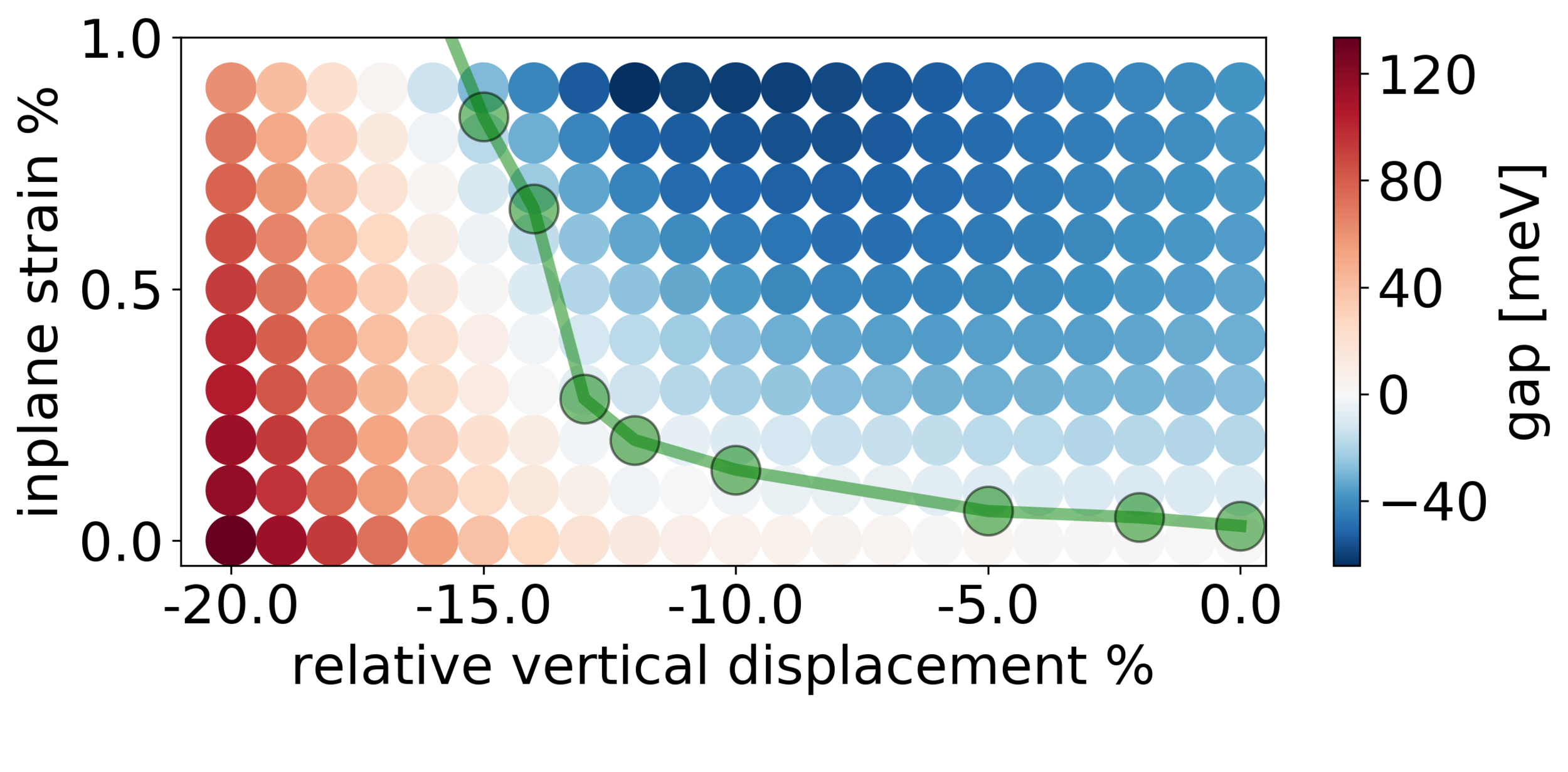
Pressure→I, inplane strain →TI !?!
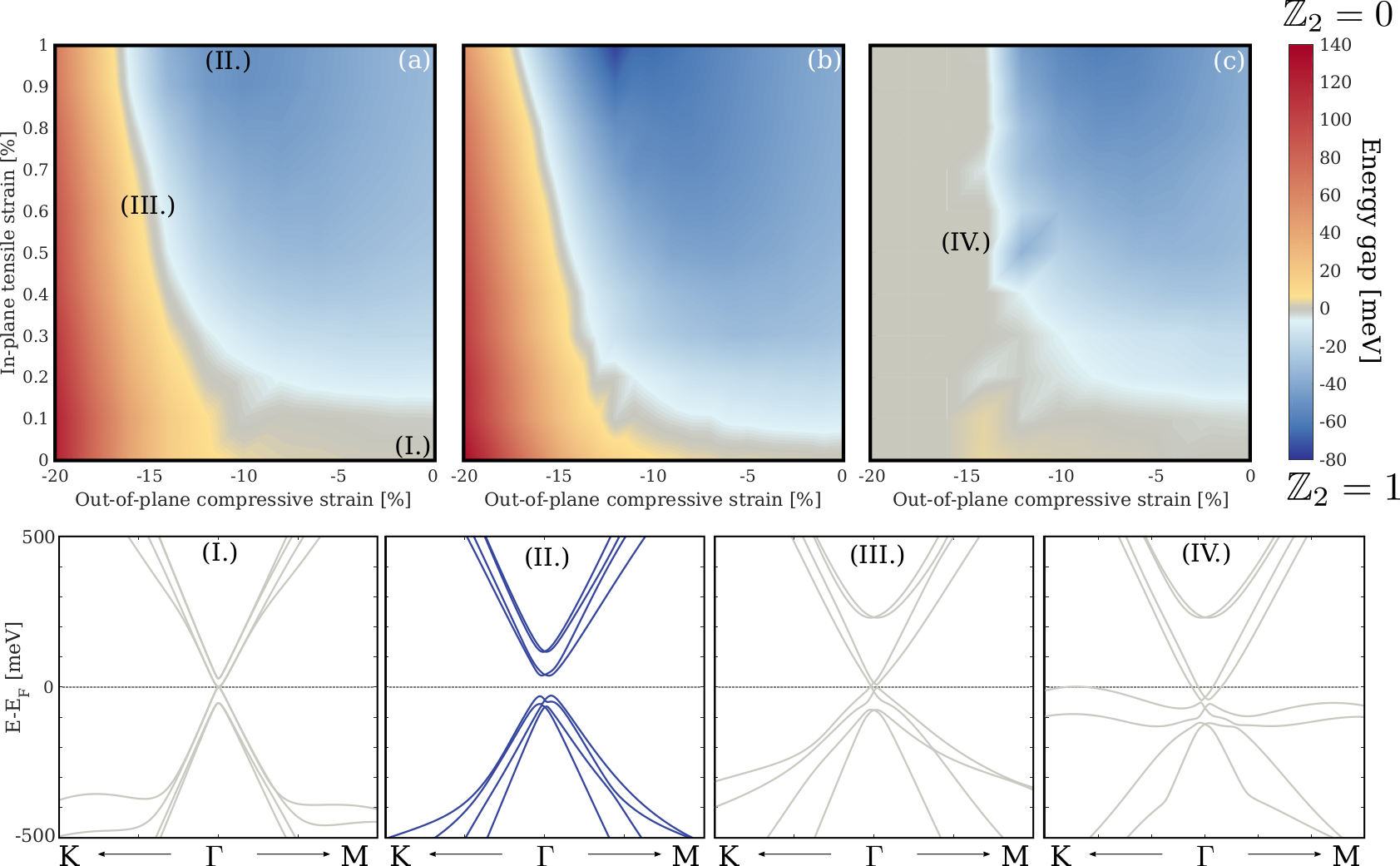
Z. Tajkov el al. Appl. Sci. 9, 4330 (2019)
BiTeBr
BiTeCl
BiTeCl
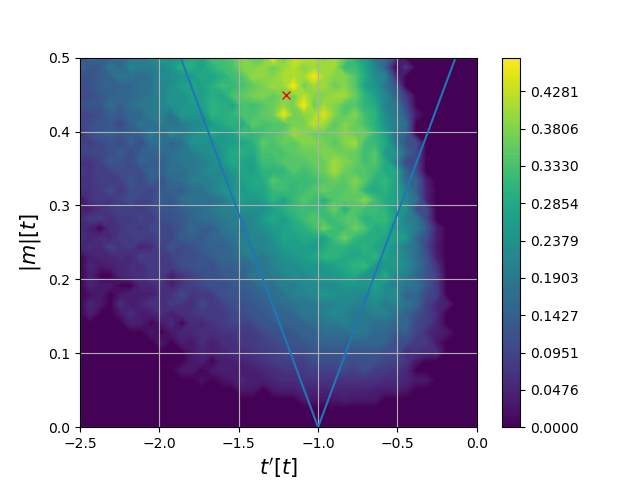
Effective model and fit

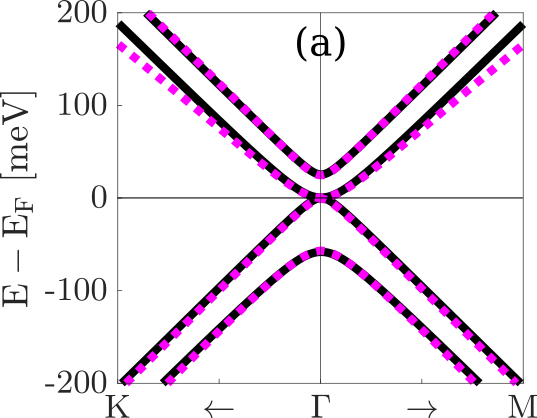
TB model predicts phase transition well!
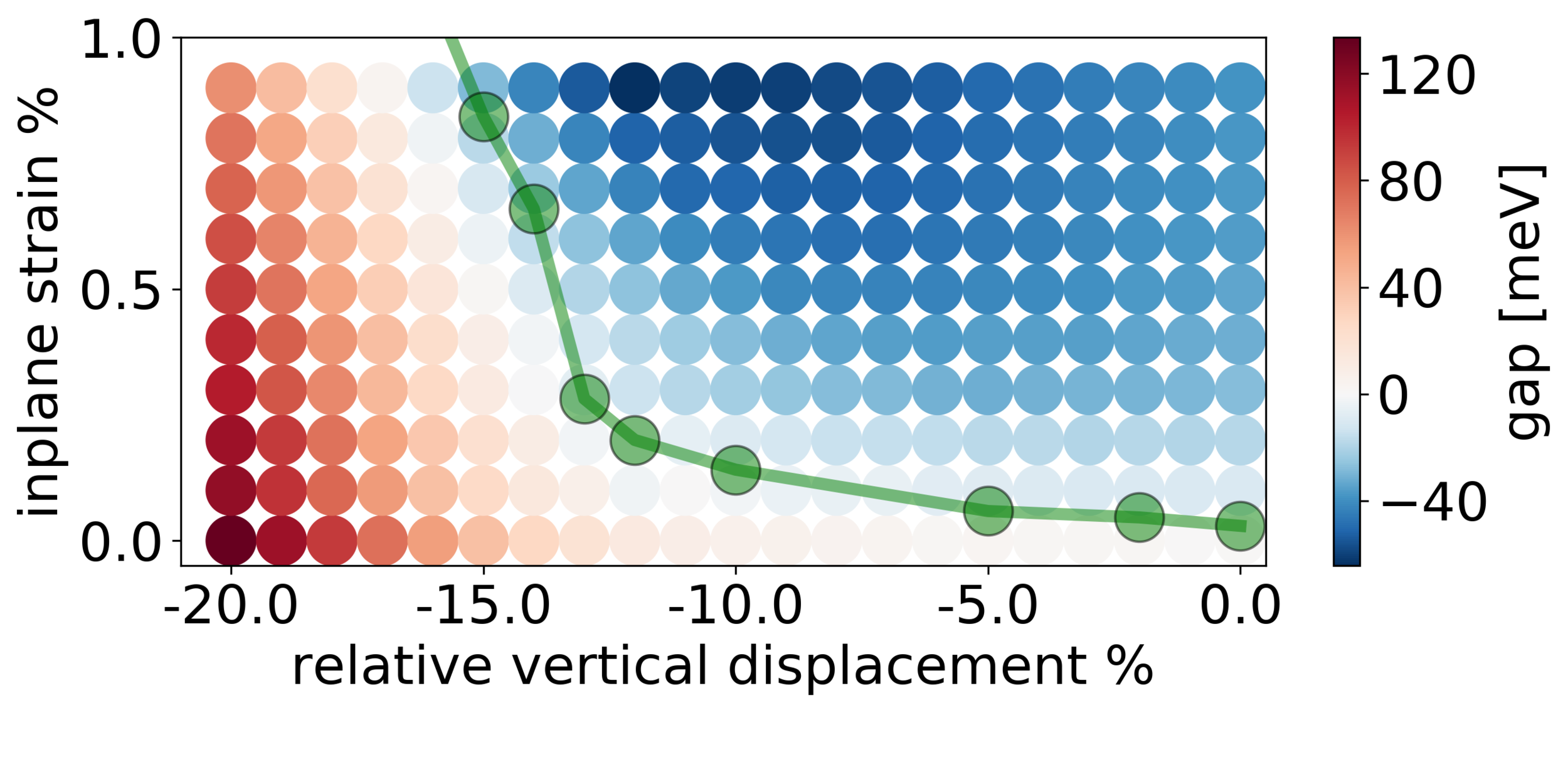
topological
trivial
Strain can close the gap at \(k=0\) if
Effective model
Gamayun et al. New J. Phys. 20, 023016 (2018)
Andrade el al. Phys. Rev. B 99, 035411 (2019)
Strain kills Kekulé but KM gap is resilient!
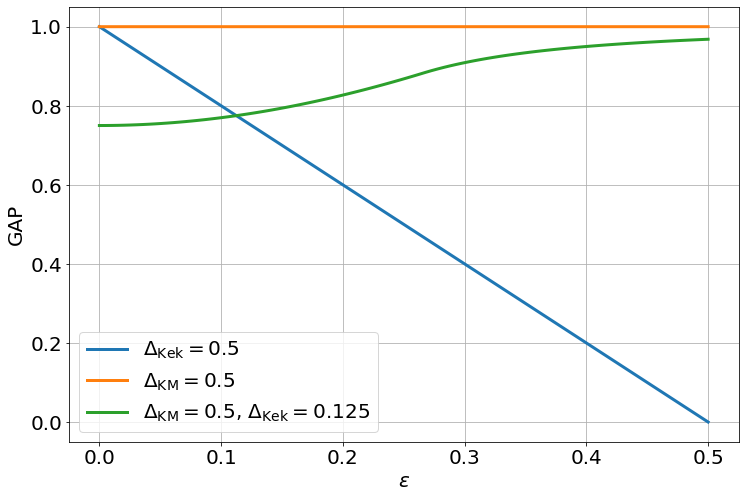

Hidden order of adatoms via RKKY
V.V.Cheianov et al. Solid State Commun. 149, 1499 (2009)

"Ferro"
"Para"
Large adatom \( \Rightarrow \) strong SOC
Disorder?
KPM!
Weiße et al. Rev. Mod. Phys. 78, 275 (2006)
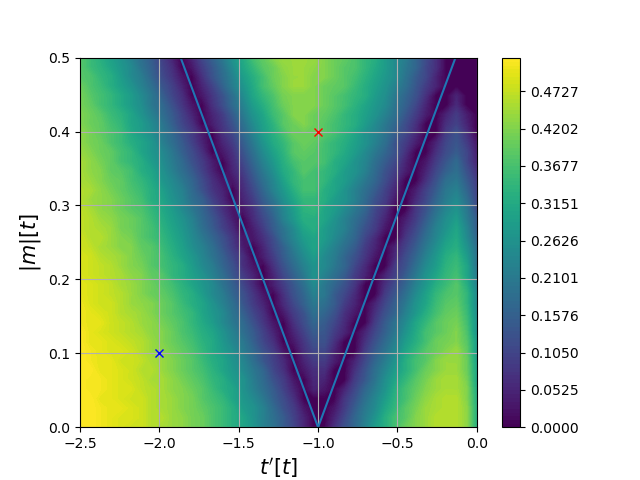
"Ferro"



"Para"
T

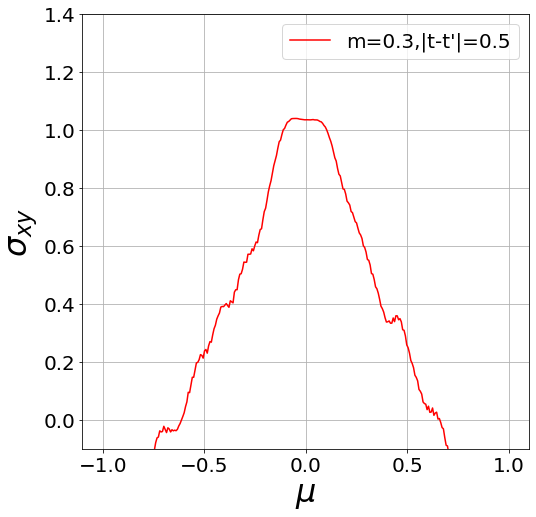
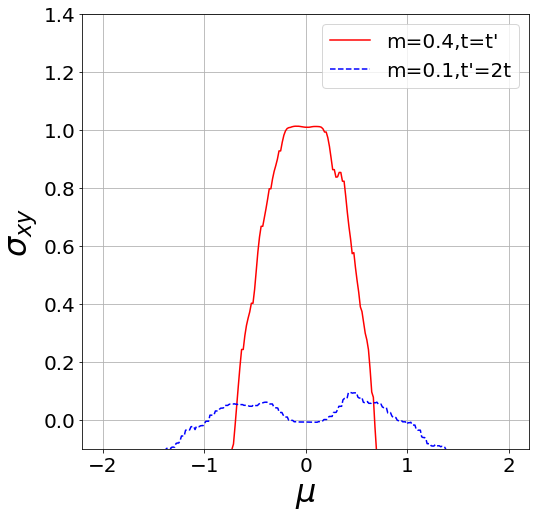

I to TI transition at finite temperature!
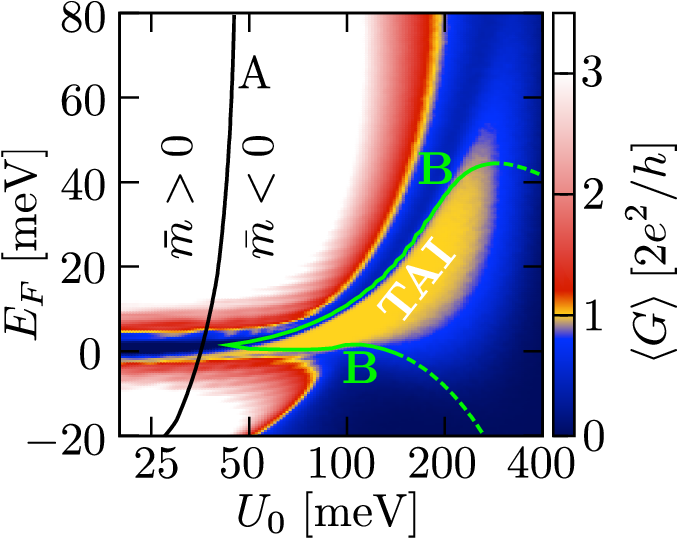
C. W. Groth, et al. Phys. Rev. Lett. 103, 196805 (2009)
The Team




Zoltán Tajkov
Dániel Nagy
János Koltai
József Cserti
Thanks!



Z. Tajkov el al. Nanoscale 11, 12704 (2019)
Z. Tajkov el al. Appl. Sci. 9, 4330 (2019)
Competition of trivial and topological phases in graphene based hybrid systems
By László Oroszlány
Competition of trivial and topological phases in graphene based hybrid systems
- 797



