2. Mai 2000

0
4
0
0
:

(UTC)

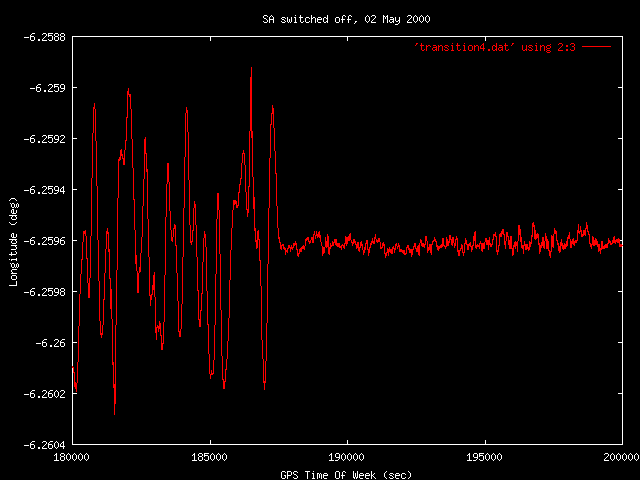
~100m

~10m

GPS

Satellitennavigation

Inhalt

  1. Koordinatensystem
  2. GPS-Satelliten
  3. GPS-Signale
  4. GPS-Fix
  5. Genauigkeit
  6. Andere Systeme

Position

O(0|0)
O(0∣0)O(0|0)
\times
×\times
\times
×\times
P(2|1.5)
P(2∣1.5)P(2|1.5)

Positionsbestimmung

Bestimmung von Abstand und Richtung eines Punktes zu einem bekannten Ursprung

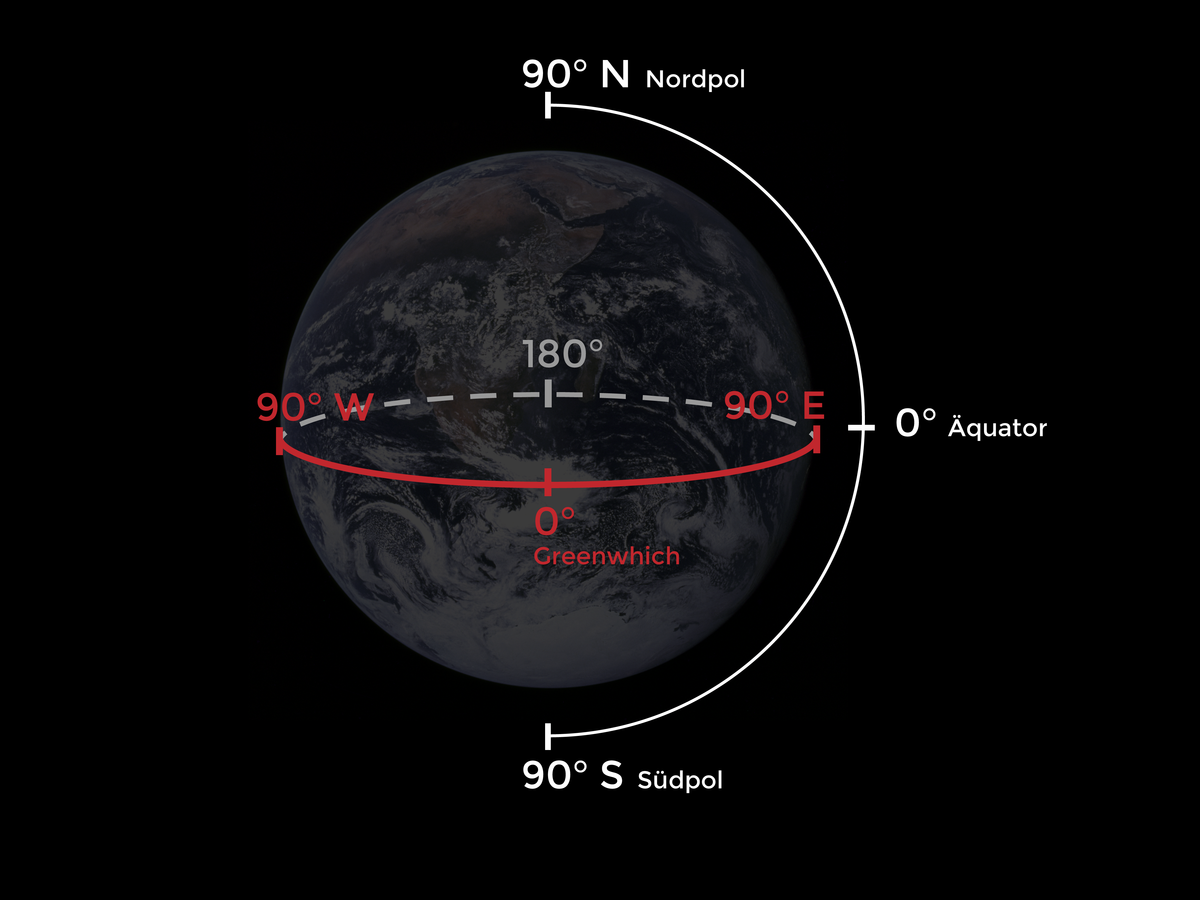
Bühl

48° N, 8° E
 

Alaska

64° N, 150° W
 

Sydney

33° S, 151° E
 

GPS

Space Segment

Control Segment

User Segment

GPS-Satelliten

Bodenstationen

GPS-Empfänger

h=26\text{ }600\text{ km}
h=26 600 kmh=26\text{ }600\text{ km}
T=11\text{ h, } 58\text{ min}
T=11 h, 58 minT=11\text{ h, } 58\text{ min}

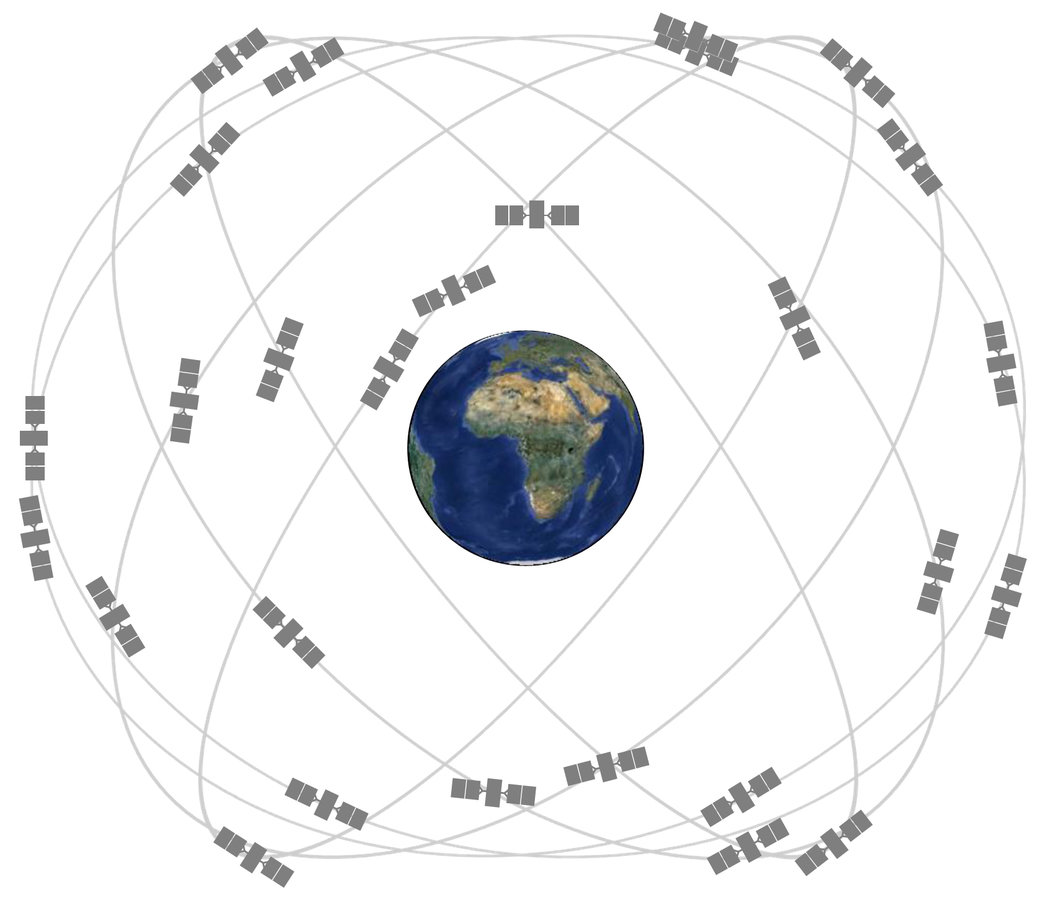
Mindestens 24 Satelliten

Von jedem Punkt min. 4

30 Satelliten

Von jedem Punkt 9-11

Modulation

1 1 0 1 1 0 0 1 0 0

Amplitudenmodulation

  • Anpassen der Amplitude an das Datensignal
  • Mittelwellenradio

Binary Phase Shift Keying

  • Phasenverschiebung der Trägerwelle um
  • Nur digitale Daten
\frac{\lambda}{2}
λ2\frac{\lambda}{2}
f_{L1}=1.57542 \text{ GHz}
fL1=1.57542 GHzf_{L1}=1.57542 \text{ GHz}

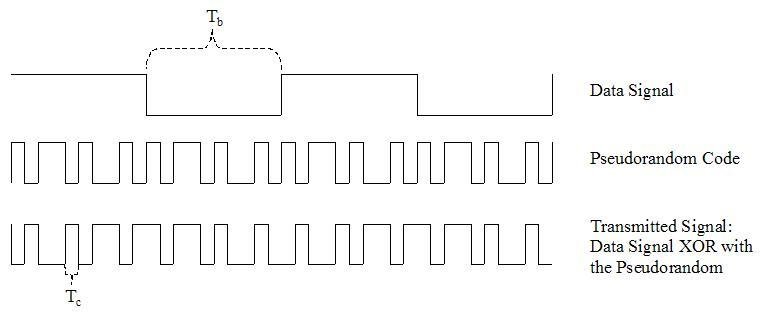
CDMA

Code Division Multiple Access

A B A XOR B
0 0 0
1 0 1
0 1 1
1 1 0

Exklusives Oder (XOR)

A\oplus{}B
A⊕BA\oplus{}B

C/A-Code

Coarse Acquicition ("Grobe Erfassung")

110010000011...

PRNG

S,V
S,VS,V

1023 Chips

1,023 MChip/s

Wiederholung nach 1ms

SV = {
   1: [2,6],
   2: [3,7],
   3: [4,8],
# ...
}

def shift(register, feedback, output):

    out = [register[i-1] for i in output]
    if len(out) > 1:
        out = sum(out) % 2
    else:
        out = out[0]

    fb = sum([register[i-1] for i in feedback]) % 2

    for i in reversed(range(len(register[1:]))):
        register[i+1] = register[i]

    register[0] = fb

    return out


def ca(svn=1):
    G1 = [1 for i in range(10)]
    G2 = [1 for i in range(10)]

    ca = []

    for i in range(1023):
        g1 = shift(G1, [3, 10], [10])
        g2 = shift(G2, [2, 3, 6, 8, 9, 10], SV[svn])
        ca.append((g1 + g2) % 2)

    return ca

Navigationsnachricht

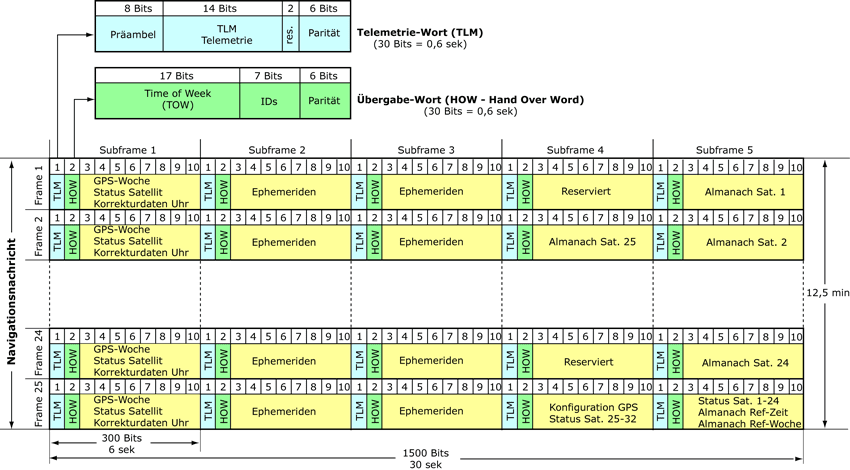
  • Präambel
  • GPS-Woche (Wochen seit 22.08.1990)
  • Zeit in der aktuellen Woche (6s-Schritte)
  • Bahndaten der Satelliten
  • Korrekturinformationen (Erdathmosphäre, Uhrzeit, etc.)
  • Differenz GPS-Zeit zu UTC

50 Bit/s

1 Bit dauert 20 ms (20 C/A-Codes)

GPS-Fix

GPS-Signal auf der Erde

  • Sehr schwach
  • Überlagern der Satelliten

Autokorrelation

Empfangenes Signal

Interner C/A-Code

Empfangen: 1

Intern: 1

1

Empfangen: 0

Intern: 1

0

Empfangen: 1

Intern: 0

0

\sum \text{ intern} \cdot \text{empfangen}
∑ intern⋅empfangen\sum \text{ intern} \cdot \text{empfangen}

Zeitverschiebung

C/A-Code wiederholt sich nach 1ms

Frequenzverschiebung

Satelliten bewegen sich mit 3,9km/s

Durch Doppler-Effekt

\pm 6\text{ kHz}
±6 kHz\pm 6\text{ kHz}

Nicht sichtbarer Satellit

Von 32 nur 9-11 sichtbar

t_i
tit_i

Code negiert

Bitwechsel

\Delta{}t=12\text{ ms}
Δt=12 ms\Delta{}t=12\text{ ms}
  • Beginn eines Subframe (alle 0,6s)
  • Beginn eines Frames (alle 6s)
  • Lesen von GPS-Zeit
  • Lesen von GPS-Woche
t_i
tit_i

Für Signale jedes Satelliten

mindestens 4

t_1,t_2,t_3,t_4,...,t_n
t1,t2,t3,t4,...,tnt_1,t_2,t_3,t_4,...,t_n

Lesen der Bahndaten aus der Navigationsnachricht

Für jeden Satelliten  

i
ii
  • Sendezeitpunkt
  • Position zum Sendezeitpunkt
t_i
tit_i
x_i,y_i,z_i
xi,yi,zix_i,y_i,z_i
(x_i - x_0)^2 + (y_i - y_0)^2 + (z_i - z_0)^2 = (c\cdot(t_0-t_i))^2
(xi−x0)2+(yi−y0)2+(zi−z0)2=(c⋅(t0−ti))2(x_i - x_0)^2 + (y_i - y_0)^2 + (z_i - z_0)^2 = (c\cdot(t_0-t_i))^2
(x_1 - x_0)^2 + (y_1 - y_0)^2 + (z_1 - z_0)^2 = (c\cdot(t_0-t_1))^2
(x1−x0)2+(y1−y0)2+(z1−z0)2=(c⋅(t0−t1))2(x_1 - x_0)^2 + (y_1 - y_0)^2 + (z_1 - z_0)^2 = (c\cdot(t_0-t_1))^2
(x_2 - x_0)^2 + (y_2 - y_0)^2 + (z_2 - z_0)^2 = (c\cdot(t_0-t_2))^2
(x2−x0)2+(y2−y0)2+(z2−z0)2=(c⋅(t0−t2))2(x_2 - x_0)^2 + (y_2 - y_0)^2 + (z_2 - z_0)^2 = (c\cdot(t_0-t_2))^2
(x_3 - x_0)^2 + (y_3 - y_0)^2 + (z_3 - z_0)^2 = (c\cdot(t_0-t_3))^2
(x3−x0)2+(y3−y0)2+(z3−z0)2=(c⋅(t0−t3))2(x_3 - x_0)^2 + (y_3 - y_0)^2 + (z_3 - z_0)^2 = (c\cdot(t_0-t_3))^2
(x_4 - x_0)^2 + (y_4 - y_0)^2 + (z_4 - z_0)^2 = (c\cdot(t_0-t_4))^2
(x4−x0)2+(y4−y0)2+(z4−z0)2=(c⋅(t0−t4))2(x_4 - x_0)^2 + (y_4 - y_0)^2 + (z_4 - z_0)^2 = (c\cdot(t_0-t_4))^2

4 Unbekannte, 4 Gleichungen

P(x_0|y_0|z_0)
P(x0∣y0∣z0)P(x_0|y_0|z_0)
t_0
t0t_0

Zum Zeitpunkt

War ich

Kaltstart

Keine/veraltete Informationen

Mehrere Minuten

Warmstart

Ungefähre Position bekannt

30-60s

Heißstart

Bekannte Daten bis zu 6h alt

Unter 10s

Korrekturen

  • Relativistische Effekte
  • Licht ist in Medium (Athmosphäre) kleiner
  • Ionosphäre

Geschwindigkeit

Spezielle Relativitätstheorie

Schwerkraft

Allgemeine Relativitätstheorie

45 µs / Tag schneller

7 µs / Tag langsamer

38 µs / Tag schneller

38 µs entspricht 10 km

GPS

GLONASS

Galileo

Beidou

gps.leonadi.de

GPS

By Leon Bentrup

Made with Slides.com

GPS

Sattelitennavigation. GFS Physik 2015

  • 918

More from Leon Bentrup