Medical image registration

    医学图像配准  是指对于一幅医学图像寻求一种 (或一系列 )空间变换 ,使它与另一幅医学图像上的对应点达到空间上的一致。 这种一致是指人体上的同一解剖点在两张匹配图像上有相同的空间位置。

    当前 ,医学图像配准的研究集中在断层扫描图像( 如CT、 MRI、SPECT、 PET 等 )及时序图像 ( 如 fMRI及 4D心动图像 )的配准问题。

图像配准原理及概念

相似性测度是一个跟变换有关并借助两幅图像数据计算出的用来衡量相似程度的函数

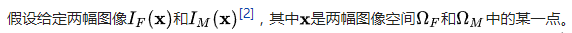
最后通过一种数学优化算法找到该函数的最优解，即变换。

配准方法的分类

1. 基于内部特征

   1. 基于特征点：在几何上有特别意义的可以定位的特征点集（比如不连续点，图形的转折点，线交叉点等），在医学图像上可以是具有解剖意义的点。           

   2. 基于表面：用分割的方法提取出感兴趣的部分的轮廓（曲线或曲面），以作为用来比较的特征空间。                                                                                   

   3. 基于像素值：利用整幅图像的像素或体素（Intensity-Based）来构成特征空间。根据像素值的统计信息来计算相似性测度又可划分。                                                                         

2. 基于外部特征                                                                                                      
   在医学图像中，通过在患者身上固定标记物或向体内注入显影物质以获得在图像上的确定的标记点，称为外部特征点。

• 根据 算法所基于的特征及相似性测度

• 根据变换性质                                                                                                   
       对图像进行空间变换可以分为刚体变换（rigid）和非刚体变换（non-rigid, deformable）。通常有刚体变换，仿射变换，投影变换和曲线变换。

• 根据优化算法                                                                                                                                                                                                  
       当比较特征采用特征点集的形式时，可以通过联立方程组来找到变换的解。但一般情况下，配准问题都会转化为求解相似性测度最优值的问题，在计算方法中通常需要采用合适的迭代优化算法

• 根据空间维数                                                                                                                                                                                                   
      若仅考虑空间维数，可以划分为2D/2D, 2D/3D, 3D/3D。若考虑时间序列因素，还存在对在不同时刻提取的两幅图像进行配准的问题。

在医学图像配准中，还可以根据以下方式：

• 根据图像模态                                                                                                       
    由于医学成像设备可以提供关于患者不同信息不同形式的图像（计算机断层扫描CT，核磁共振MRI，正电子发射断层成像PET，功能核磁共振fMRI等），所以根据模态又可以划分为单模态和多模态（Multi-modal）

• 根据主体                                                                                                             
    可分为Intrasubject（图像来自于同一病人），Intersubject（来自不同的病人）和Atlas（病人数据和图谱的配准）三种。

对齐的质量由距离或相似性度量S定义，例如平方差之和（SSD），相关比或互信息（MI）度量。均方差（MSD） 规范化互信息（NMI）Kappa统计（KS）

• MSD 用于来自相同模态的图像。                                                  
• MI度量  不仅适用于单模态，而且适用于多模态图像对。 这种测量通常是图像配准的好选择。                                                       
• NMI  适用于单模和多模态配准。                                                
• KS 专门用于配准二进制图像（分段）。它衡量分的的“重叠”

评估配准

计算配准后分割解剖结构的重叠。 重叠越好，配准越好。  为了测量重叠，通常使用骰子相似系数（DSC）

其中X和Y表示二进制标签图像，和| ·| 表示等于1的体素数。较高的DSC表示较好的对应关系。 值1表示完全重叠，值0表示完全不重叠。

  not always suitable for biomedical images, since there are few reliable and distinguishable features (e.g. corners) and weak constraints on the deformation field

(e.g. Distinctive image features from scale-invariant keypoints )

Feature-based methods

pixel-based methods

     methods based on minimizing a pixel-based image similarity criterion, are often slow .

     Luckily, it turns out that criterion evaluation can be simplified, without compromising registration accuracy too much

(e.g. Fast Registration by Boundary Sampling and Linear Programming)

Traditional methods to find the optimal deformation field mapping two images rely on the optimization of a     matching criteria controlling the local correspondence of the voxel intensities.

These methods usually have several drawbacks:

• high computational cost (time and memory)
•  requires many iterations and evaluations of the energy function
• may stuck in a local minimum 

Traditional methods

•     Most of these rely on ground truth warp fields or segmentations                                                                  
•    only demonstrated on limited subsets of volumes, such as 3D subregions or 2D slices, and support only small transformations.

Learning-based methods

       Most existing registration algorithms iteratively optimize a transformation based on an energy function.

       The optimization problem is typically written as:

    F , M denote the fixed and moving images, and  denote the registration field.

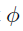
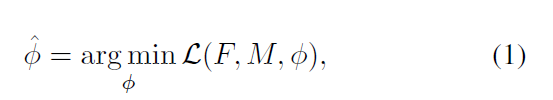
Problem 

is a displacement vector field, specifying
the vector offset from F to M for each voxel.

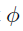
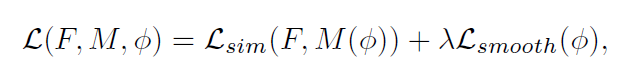
&& Optical flow estimation

• Optical flow estimation is an analogous problem to 3D volume registration for 2D images                              
• Optical flow algorithms return a dense displacement vector field depicting small displacements between a 2D image pair                                                                   
• Traditional optical flow approaches typically solve an optimization problem similar to (1)  using variational methods