
En 5 minutos...
Introducción a
imposible


Mencionar algunas de las
características más importantes de


Antes... datos curiosos
- 333 contribuyentes
- 1,058 forks
- 22,963 commits
- En 2012 todos los contribuyentes excepto los autores llevaban 6 meses conociendo el lenguaje.

We want a language that’s open source, with a liberal license. We want the speed of C with the dynamism of Ruby. We want a language that’s homoiconic (i.e., has the same representation of code and data), with true macros like Lisp, but with obvious, familiar mathematical notation like MATLAB. We want something as usable for general programming as Python, as easy for statistics as R, as natural for string processing as Perl, as powerful for linear algebra as MATLAB, as good at gluing programs together as the shell. Something that is dirt simple to learn, yet keeps the most serious hackers happy. We want it interactive and we want it compiled. … We want to write simple scalar loops that compile down to tight machine code using just the registers on a single CPU. We want to write A*B and launch a thousand computations on a thousand machines, calculating a vast matrix product together.
Why Julia?
Because we are greeedy

Puntos clave
para mi...
- Compatibilidad
- Simplicidad
- Velocidad
Además de que es open source y todo eso...
Compatibilidad

Compatibilidad




Julia -> python -> Julia -> python...
- PyCall.jl
- run(...)
- Rif.jl
Compatibilidad


Ejemplo
run(`curl https://www.gutenberg.org/cache/epub/2265/pg2265.txt` |>
`tr -s "[:upper:]" "[:lower:]"` |>
`grep -oE "\w+"` |>
`grep -v "[0-9]"` |>
`sort` |>
`uniq -c` |>
`sort -rn` |>
`head -10`)
10 palabras más frecuentes en Hamlet
Simplicidad

Simplicidad

Añadir paquetes
- Pkg.add()
- Pkg.clone()
Sintáxis
julia> x = reshape(1:16, 4, 4)
4x4 Array{Int64,2}:
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
julia> x[2:3, 2:end-1]
2x2 Array{Int64,2}:
6 10
7 11Simplicidad

Ejemplo (proyecto)
# Investigación de operaciones.
# Luis Manuel Román García
# 000117077
# En este código se verifica que la gráfica este conectada.
using Distributions
#using Gadfly
function genGraph(net_length)
#Genera de manera aleatoria una gráfica.
#IN
#net_length = el tamaño de la red.
#OUT
#matriz de vértices.
edgeMatrix = reshape(rand(DiscreteUniform(1,net_length), net_length*2),net_length,2)
vcat(edgeMatrix,edgeMatrix[:,[2,1]])
end
function adjacency(graph, node)
#Encuentra los nodos adjacentes a un nodo dado.
#IN
#node = el nodo del cual se quieren encontrar los nodos adjacentes
#graph = la gráfica sobre la cuál se hará la búsqueda
#OUT
#adj = el conjunto de nodos adjacentes al nodo dado.
g_length = length(graph[:, 1])
adj = Int64[]
for i = 1:g_length
if graph[i, 1] == node
push!(adj, graph[i, 2])
end
end
return unique(adj)
end
function recorrido(graph, node, check)
# Recorre la gráfica a partir de un nodo y verifica si esta está conectada.
# IN
# graph: la gráfica sobre la que se quiere hacer el recorrido.
# node: el nodo a partir del cual se inicia la búsqueda (default 1).
# check: los nodos que han sido verificados hasta el momento (default 0).
# cycle: determina si la gráfica tiene ciclos, default false
# tree: un árbol asociado a la gráfica (default la)
# OUT
# variable lógica que determina si la gráfica está conectada.
check[node] = 1 #Marcar el nodo como verificado.
adj = adjacency(graph, node) #Obtener los nodos adjacentes al nodo i.
for j in adj
if check[j] == 0 && sum(check[adj]) != length(adj) #Verifica si el nodo está marcado y si tiene vecinos no marcados.
recorrido(graph, j, check)
elseif sum(check[adj]) == length(adj) # Si todos sus vecinos están marcados lo marcamos
check[j] = 1
end
end
if sum(check) == length(unique(graph[:, 1]))
return true
else
return false
end
end
function spanningTree(graph)
# Recorre la gráfica a partir de un nodo y construye un árbol de expansión.
# IN
# graph: la gráfica sobre la que se quiere hacer el árbol.
# OUT
# Un árbol de expansión en caso de que la gráfica este conectada,
# de lo contrario un mensaje.
check = zeros(length(unique(graph[:,1])),1)
node = 1
if recorrido(graph, node, check) == true
print("gráfica conectada")
tree = zeros(1,2)
bag = []
for i in unique(graph[:,1])
bag = vcat(bag,i)
for j in adjacency(graph, i)
if !(j in bag)
bag = vcat(bag,j)
tree = vcat(tree,[i j])
end
end
end
return tree[2:end,[1, 2]]
else
return "gráfica no conectada"
end
end
function input(prompt::String="")
# Leer inputs del usuario.
print(prompt)
chomp(readline())
end
#######
#Run
#######
#graph = input("Gráfica:")
#println(spanningTree(graph))
functions.jl
# En este script se pone a prueba el algoritmo spanningTree
graph1 = [1 2; 2 3; 3 4; 2 1; 3 2; 4 3]
graph2 = [1 2; 1 4; 2 3; 3 4; 4 1; 2 1; 4 1; 3 2; 4 3; 1 4]
graph3 = [1 2; 3 4; 2 1; 4 3]
graph4 = [1 2; 1 3; 2 3; 2 5; 3 4; 3 5; 4 5; 2 1; 3 1; 3 2; 5 2; 4 3; 5 3; 5 4]
spanningTree(graph1)
spanningTree(graph2)
spanningTree(graph3)
spanningTree(graph4)
Main.jl
Velocidad

Velocidad
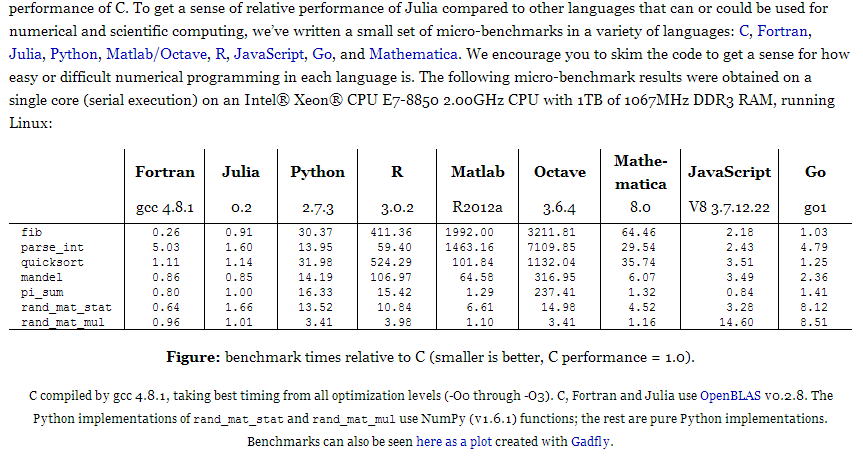

Velocidad

Procesamiento en pralelo
Números aleatorios (paralelo)
Números aleatorios (normal)
tic()
a = zeros(100000)
@parallel for i=1:100000
a[i] = i
end
toc()
elapsed time: 0.585655953 seconds
tic()
a = zeros(100000)
for i=1:100000
a[i] = i
end
toc()
elapsed time: 1.710980293 seconds
Más de 3 veces más rápido
FIN
Julia
By Luis Roman
Julia
- 1,306



