On the Use of Second Order Stochastic Information
for Learning Deep Artificial Neural Network
Presentation Overview
- State of the intelligence
- Deep Artificial Neural Networks
- The promises of second order methods
- Conclusion
State of the intelligence
2010
The breakthrough of Deep Artificial Neural Networks
Images
Speech
Language
drug effectiveness | particle acceleration |brain circuit reconstruction | predicting DNA mutation effects | topic classification |
sentiment analysis | question answering | video processing | creative computing | language translation | time series analysis
2011
Watson competed on Jeopardy! against former winners Brad Rutter and Ken Jennings Watson received the first place prize of $1 million.
2010
2011
2012
2013
2014
2015
70%
75%
80%
85%
90%
95%
CNN
Traditional
Historical top5 precision of the annual winner of the ImageNet challenge
2016
Alphago The first computer program to ever beat a professional player at the game of Go
2016
The ConceptNet 4 system has been put through a verbal IQ test, getting a score that is seen as “average for a four-year-old child”.
Poem 1
And lying sleeping on an open bed.
And I remember having started tripping,
Or any angel hanging overhead,
Without another cup of coffee dripping.
Surrounded by a pretty little sergeant,
Another morning at an early crawl.
And from the other side of my apartment,
An empty room behind the inner wall.
Poem 2
A green nub pushes up from moist, dark soil.
Three weeks without stirring, now without strife
From the unknown depths of a thumbpot life
In patient rhythm slides forth without turmoil,
A tiny green thing poking through its sheath.
Shall I see the world? Yes, it is bright.
Silent and slow it stretches for the light
And opens, uncurling, above and beneath.
Who is the human?
2016
the development of full artificial intelligence could spell the end of the human race
- Stephen Hawking
2018
the development of Video-to-video Synthesis now perfect replications can be created of individuals in videos
Deep Artificial Neural Networks
Where learnability comes from?
Deep learning methods are representation-learning methods with multiple levels of representation
Composition of several layers can learn very complex functions efficiently
Example architecture: LSTM
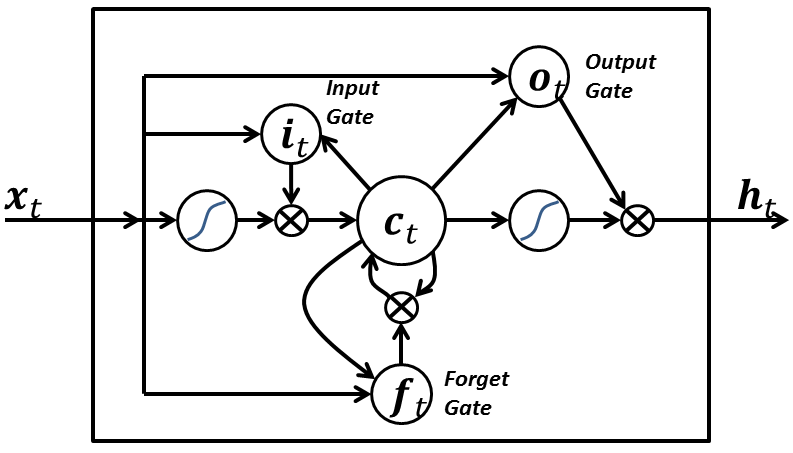
The problem is that they are very difficult to train:
- Non linear
- Non convex
The tool of choice for training is stochastic gradient descent which misbehaves under scenarios with high non linearities
Stochastic gradient descent
wk+1=wk−α∇l(h(xi,wk))
w_{k+1} = w_k - \alpha\nabla l(h(x_i, w_k))
Under some regularity assumptions, the best we can expect is sub linear convergence:
Best case scenario
E[F(wk)−F(w∗)]≤2cμα^LM+(1−α^)k−1(F(w1)−F(w∗)−2cμα^LM)
\mathbb{E}[F(w_k)- F(w^*)] \leq \frac{\hat{\alpha}LM}{2c\mu} + (1-\hat{\alpha})^{k-1}\Big(F(w_1)-F(w^*)-\frac{\hat{\alpha} LM}{2c\mu}\Big)
In an online scenario:
Best case scenario
regretT≤23GDT
regret_T \leq \frac{3}{2}GD\sqrt{T}
The promises of second order methods
Second order methods
wk+1=wk−αH(∣S∣k)∣X∣k1i=1∑∣X∣k∇l(hwk)
w_{k+1} = w_k - \alpha H_{(|S|_k)} \frac{1}{|X|_k}\displaystyle\sum_{i=1}^{|X|_k}\nabla l(h_{w_k})
∣S∣k≤∣X∣k
|S|_k\leq |X|_k
Under some regularity assumptions, the best we can expect is super linear - quadratic convergence:
Best case scenario
∣Xk∣≥∣X0∣ηkk;∣X0∣≥(μ^26vγM),ηk>ηk−1,ηk→∞,η1>1
|X_k| \geq |X_0|\eta_k^k;\quad |X_0|\geq\bigg(\frac{6v\gamma M}{\hat{\mu}^2}\bigg), \eta_k > \eta_{k-1}, \eta_k \rightarrow\infty, \eta_1>1
∣Sk∣>∣Sk−1∣;k→∞lim∣Sk∣=∞;∣S0∣≥(μ^4σ)2
|S_k| > |S_{k-1}|;\quad \displaystyle\lim_{k\rightarrow\infty}|S_k|=\infty; \quad |S_0|\geq\bigg(\frac{4\sigma}{\hat{\mu}}\bigg)^2
∥w0−w∗∥≤3γMμ^
\|w_0-w^*\|\leq\frac{\hat{\mu}}{3\gamma M}
E[∣wk−w∗∣]≤τkk→∞limτkτk+1→0
\mathbb{E}[|w_k - w^*|]\leq\tau_k\quad\quad\displaystyle\lim_{k\rightarrow\infty}\frac{\tau_{k+1}}{\tau_k}\rightarrow 0
In an online scenario regret grows O(log(T)):
Best case scenario
γ=21min{4GD1,α},ϵ=γ2D21
\gamma = \frac{1}{2}\min\{\frac{1}{4GD}, \alpha\}, \epsilon = \frac{1}{\gamma^2 D^2}
regretT≤5(α1+GD)nlog(T)
regret_T \leq 5(\frac{1}{\alpha}+ GD)n\log(T)
The multiple advantages of second order methods:
- Faster convergence rate
- Embarrassingly parallel
- Take into consideration curvature information
- Ideal for highly varying functions
- Higher per iteration cost
2010-2016
-
Martens is the first to successfully train a deep convolutional neural network with L-BFGS.
-
Sutskever successfully trains a recurrent neural network with a generalized Gauss-Newton algorithm
-
Bengio achieves state of the art results training recurrent networks with second order methods
Conclusion
On the Use of Second Order Stochastic Information for Learning Deep Artificial Neural Network
Second Order Methods for
By Luis Roman
Second Order Methods for
- 1,176
