Shapley–Shubik power index

Shapley–Shubik power index

One of the indicators used to present the political power of an actor participating in the decision-making process within a collegiate body, proposed in 1954 by the authors whose names it took its name from.

Shapley–Shubik power index

What are

indexes /indices / indicators of power?

Shapley–Shubik power index

The power indices can be simply defined as:

functions that determine the position of individual participants in the decision-making assembly in view of the demand for them in the formation

of the winning coalitions

M. Jasiński, Czy zawsze większy jest silniejszy,
czyli jak zmierzyć siłę uczestników zgromadzeń
decyzyjnych, „Studia Socjologiczne” 2000,
nr 1-2(156-157), s. 50.

Shapley–Shubik power index

Shapley–Shubik power index is one of the

a priori indexes 

that is, treating each variant of the coalition as equally probable, regardless of the actual ideological distance between the players, personal relations, etc.

Shapley–Shubik power index

About the study of the ideological distance between players and indexes different than a priori:

• M. Mazurkiewicz, J. Mercik, Modified Shapley–Shubik Power Index for Parliamentary Coalitions, „Badania Operacyjne i Decyzje” 2005, nr 2, s. 43-52.
• M. Bożykowski, M. Jasiński, Struktura cząstkowej jednolitości graczy a ich znaczenie w zgromadzeniu. Hybrydowe indeksy siły, „Decyzje” 2014, nr 2, s. 5-29.
• M. Jasiński, Przestrzeń ideologiczna oparta na politycznych faktach, „Decyzje” 2012, nr 17, s. 5-28.

Shapley–Shubik power index

We will define the game in a collegiate body as:

{q: si; sj; sk}

where:

• si is the player's weight and (the number of seats for a given grouping)
• q is the weight required from the coalition to be a winning coalition.

Shapley–Shubik power index

A coalition is a subset of the game's participants.

For example: for 3 players A, B, C, coalitions are possible:

• ABC
• ACB
• BAC
• BCA
• CAB
• CBA

and, theoretically, their shorter versions (eg AB instead of ABC), however these shorter versions are been taken in consideration only for the stage of building the coalitions.

Shapley–Shubik power index

• A coalition is a loosing coalition if the sum of the weights of its players is less than q.

for example:

the game is: {7: 3; 3; 3; 4}

the coalition {A; B} has the strength of 6 (3+3), so it is loosing coaliction.

Shapley–Shubik power index

• A coalition is a winning coalition if the sum of the weights of its players is not less than q.

for example:

the game is: {7: 3; 3; 3; 4}

the coalition {A; B; C} has the strength of 9 (3+3+3), so it is winning coaliction.

Also coalition {A; C} is winning coalition because of strength of 7 (3+4).

Shapley–Shubik power index

If, as a result of joining a player i to the losing coalition (weighing less than q), that coalition becomes a winning coalition, we define the player as
having a decisive position (decisive voter).

for example

the game is: {7: 2; 3; 1; 4; 3}

coalition-building process is:

A; B; C; D; E; F => 2; 3; 1; 4; 3

The Player E is decisive voter

[2; +3=5; +1=6; +4=10; +3=13}

Shapley–Shubik power index

The value of the Shapley-Shubik power index for player i (φi) is equal to the percentage of coalitions (taking into account the order in which they are built) in which player i is the decisive voter (deciding player).

Shapley–Shubik power index

φ {phi}

Shapley–Shubik power index

This coefficient has several important features:

• The value of φi ranges from 0 to 1, which allows it to be used in a comparative analysis.
• The sum of the φ for all players in the game is 1.
• If φi = 1, the player i has full control over the decision-making process in the council. Such a player is referred a dictator.
• If φi = 0, player i is irrelevant. That means there is no winning coalition formed by joining the player i to the losing coalition.

Shapley–Shubik power index

For the Shapley-Shubik strength index, an alternative can be indicated in the form of an analysis of a simpler (and more intuitive) index, which is:

the share in the set of seats.

Would it make sense?

Shapley–Shubik power index

For the Shapley-Shubik strength index, an alternative can be indicated in the form of an analysis of a simpler (and more intuitive) index, which is:

the share in the set of seats.

It should be noted, however, that this would lead to different results each time, the cognitive value of which would be limited.

Shapley–Shubik power index

The frequency of obtaining a share in the set of seats that makes it impossible for the party i to build a minimum winning coalition is not equal to the frequency of obtaining a zero share in the set of seats, although obtaining the result si = 0 without the slightest doubt results in obtaining the position of an insignificant player.

Shapley–Shubik power index

However, φi = 0 can may be obtained even by the party that aquired some seats. Moreover, this does not only apply to situations where another party obtains an absolute majority of seats.

Let's look at the following game (mandate distribution) and its consequences:

{12: 8; 7; 5; 3}

{12: 8; 7; 5; 3}

• How many possible coalitions (combinations) are there?
• In how many variants do individual players gain a decisive position?
• What is the φ value for the parties?

{12: 8; 7; 5; 3}

• The number of possible permutations is 4! = 24.
• The number of variants in which individual players achieve the decisive position is as follows: {8; 8; 8; 0}
• φi = {0.333; 0.333; 0.333; 0}.

{12: 8; 7; 5; 3}

Despite the fact that the fourth of the committees obtained 3 seats in the 23-seat council (13.04%), there is no minimum winning coalition created by adding this party to the losing coalition. A coalition formed by any two of the three stronger players is a winning one, so adding another player would be unjustified.

Shapley–Shubik power index

Next question:

Is gaining the highest coalition potential (regardless of the approach to the situation of draws) the same as gaining the highest number of seats?

Shapley–Shubik power index

Obtaining the highest coalition potential (regardless of the approach to the situation of draws) is not the same as winning the highest number of seats.

The value of the Shapley-Shubik power index, and hence the coalition potential, depends on the specific weight distribution between individual players, not only on the participation of the player under consideration.

Let's look at the following mandate breakdown and its ramifications:

{8: 7; 7; 1}

{8: 7; 7; 1}

• How many possible coalitions (combinations) are there?
• In how many variants do individual players gain a decisive position?
• What is the φ value for the parties?

{8: 7; 7; 1}

• The number of possible permutations is 3! = 6.
• The number of variants in which individual players gain a decisive position is as follows: {2; 2; 2} (a coalition of every two players is a winning coalition)
• φi = {0.333; 0.333; 0.333}.

The strength of each player is equal despite the clear difference (seven times more!!!!) in the share in the set of tickets.

Shapley–Shubik power index

To dispel the doubts of the previous example, lets consider a scenario where there are no ties in the number of seats:

{8: 6; 5; 4}

{8: 6; 5; 4}

φ for all players will be identical again ({0.333; 0.333; 0.333}). Although the first player earned a standalone relative majority of seats (relative majority excluding draws), his actual strength as measured by the Shapley-Shubik strength index does not exceed that of each of the other two players.

Shapley–Shubik power index

Excercise 1:

Calculate the values of the Shapley-Shubik power index for the parties in the Polish Sejm in the composition elected in 2019.

(Party: number of seats)

• PiS: 235
• KO: 134
• SLD: 49
• PSL: 30
• KONF: 11
• MN: 1

Shapley–Shubik power index

Zadanie:

The values of the Shapley-Shubik power index for the parties in the Polish Sejm in the composition elected in 2019.

• PiS: 1
• KO: 0
• SLD: 0
• PSL: 0
• KONF: 0
• MN: 0

Shapley–Shubik power index

Task 2:

Calculate the values of the Shapley-Shubik power index for parties in the Polish Senate in the 2019 composition.

• PiS: 48
• KO: 43
• PSL: 3
• SLD: 2
• Demokracja Obywatelska: 1
• Lidia Staroń: 1
• Krzysztof Kwiatkowski: 1
• Wadim Tyszkiewicz: 1

Shapley–Shubik power index

Exercise 2:

Calculation of the Shapley-Shubik power index for the party in the Polish Senate elected in 2019.

(8! = 40,320)

• PiS: 0.553572
• KO: 0.110714
• PSL: 0.110714
• SLD: 0.086905
• DB: 0.034524
• LS: 0.034524
• KK: 0.034524
• WT: 0.034524

Shapley–Shubik power index

Shapley–Shubik power index

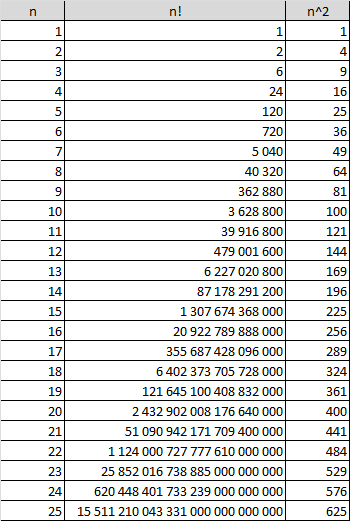
Shapley–Shubik power index

Shapley–Shubik power index

Zadanie 3:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r. ale z uwzględnieniem faktycznych bloków:

• PiS: 49
• KO: 46
• PSL: 3
• SLD: 2

Shapley–Shubik power index

Zadanie 3:

Obliczenie wartości indeksu siły Shapleya-Shubika dla partii w polskim Senacie w składzie wybranym w 2019 r. ale z uwzględnieniem faktycznych bloków:

• PiS: 0.500000
• KO: 0.166667
• PSL: 0.166667
• SLD: 0.166667