Model rywalizacji o władzę wykonawczą w Sejmikach Województw od roku 1998
Dr Maciej Onasz Katedra Systemów Politycznych Uniwersytet Łódzki
Pytania badawcze
- Jaka jest siła polityczna ugrupowań rządzących w województwach - zarówno na poziomie marszałka jak i całego zarządu.
- Czy przewodniczenie władzy wykonawczej w województwie wymaga zwycięstwa wyborczego (największa siła polityczna)
- Czy wynik wyborczy jest wystarczającą zmienną determinującą udział w rządzeniu województwem?
Założenia i metody
Jak określić siłę polityczną ugrupowania w ogranie kolegialnym?
- [tradycyjnie] liczba mandatów (względnie - udział % w mandatach),
- [alternatywa] wskaźnik obrazujący możliwość tworzenia zwycięskich koalicji (większości). Np. indeksy siły.
Indeksy siły
funkcje, które określają pozycję poszczególnych uczestników zgromadzenia podejmującego decyzję ze względu na zapotrzebowanie na nich przy tworzeniu koalicji wygrywających
M. Jasiński, Czy zawsze większy jest silniejszy,
czyli jak zmierzyć siłę uczestników zgromadzeń
decyzyjnych, „Studia Socjologiczne” 2000,
nr 1-2(156-157), s. 50.
Indeks siły Shapleya-Shubika
Jeden ze wskaźników służących przedstawieniu siły politycznej aktora uczestniczącego w procesie decyzyjnym w ramach ciała kolegialnego, zaproponowany w roku 1954 przez autorów od których nazwisk przyjął swą nazwę.
Jest jednym z tzw. indeksów a priori tzn. traktujących każdy wariant koalicji jako równie prawdopodobny, niezależnie od faktycznego dystansu ideologicznego między graczami, relacji personalnych etc.
Indeks siły Shapleya-Shubika
Grę w ciele kolegialnym zapiszemy w postaci:
{q: si; sj; sk}
gdzie:
- si oznacza wagę gracza i (liczbę mandatów danego ugrupowania)
- q wagę wymaganą od koalicji żeby była koalicją wygrywającą. Podzbiór uczestników gry stanowi koalicję.
Indeks siły Shapleya-Shubika
Koalicja jest koalicją wygrywającą jeśli suma wag tworzących ją graczy jest nie mniejsza niż q. Jeżeli w wyniku przyłączenia gracza i do koalicji przegrywającej (o wadze niższej niż q) staje się ona koalicją wygrywającą, gracza i określamy jako posiadającego pozycję decydującą (wyborcę decydującego).
Wartość indeksu siły Shapleya-Shubika dla gracza i (φi) jest równa odsetkowi koalicji (uwzględniając kolejność ich budowania), w których gracz i jest graczem decydującym.
Indeks siły Shapleya-Shubika
Koalicja jest koalicją wygrywającą jeśli suma wag tworzących ją graczy jest nie mniejsza niż q. Jeżeli w wyniku przyłączenia gracza i do koalicji przegrywającej (o wadze niższej niż q) staje się ona koalicją wygrywającą, gracza i określamy jako posiadającego pozycję decydującą (wyborcę decydującego).
Wartość indeksu siły Shapleya-Shubika dla gracza i (φi) jest równa odsetkowi koalicji (uwzględniając kolejność ich budowania), w których gracz i jest graczem decydującym.
Indeks siły Shapleya-Shubika
Współczynnik ten posiada kilka istotnych cech:
- Wartość φi zawiera się w przedziale od 0 do 1, co pozwala na wykorzystanie go w analizie porównawczej.
- Suma wartości φ dla wszystkich graczy w danej grze jest równa 1.
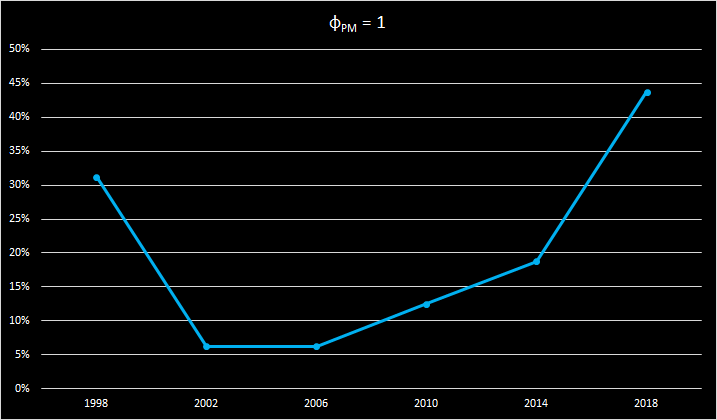
- Jeżeli φi=1, gracz i posiada pełną kontrolę nad procesem decyzyjnym w danym organie. Takiego gracza określa się mianem dyktatora.
- Jeżeli φi=0, gracz i jest graczem nieistotnym,. Tj. nie istnieje żadna koalicja wygrywająca powstała przez przyłączenie się gracza i do koalicji przegrywającej.
Dane
- Wyniki wyborów sejmików województw 1998-2018 [PKW, KBW].
- Wybrani marszałkowie oraz skład koalicji na podstawie udziału w zarządzie województwa [BIP].
Wartość indeksu siły Partii Marszałkowksiej
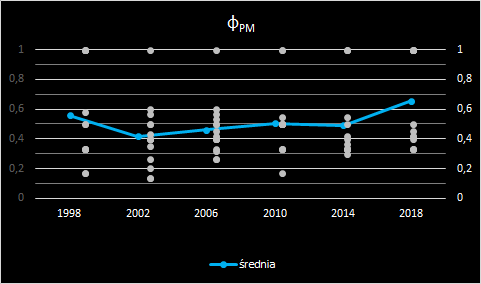
Wartość indeksu siły Partii Marszałkowksiej
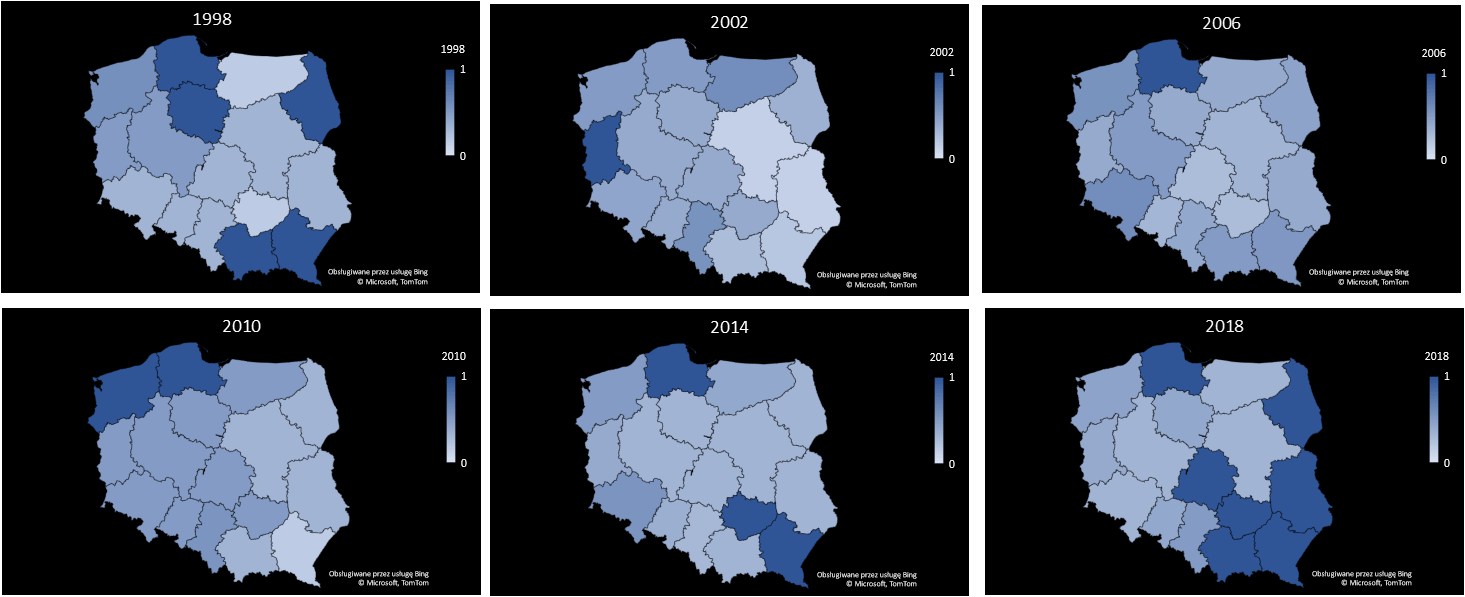
Częstość uzyskiwania pozycji dyktatora przez Partię Marszalkowską
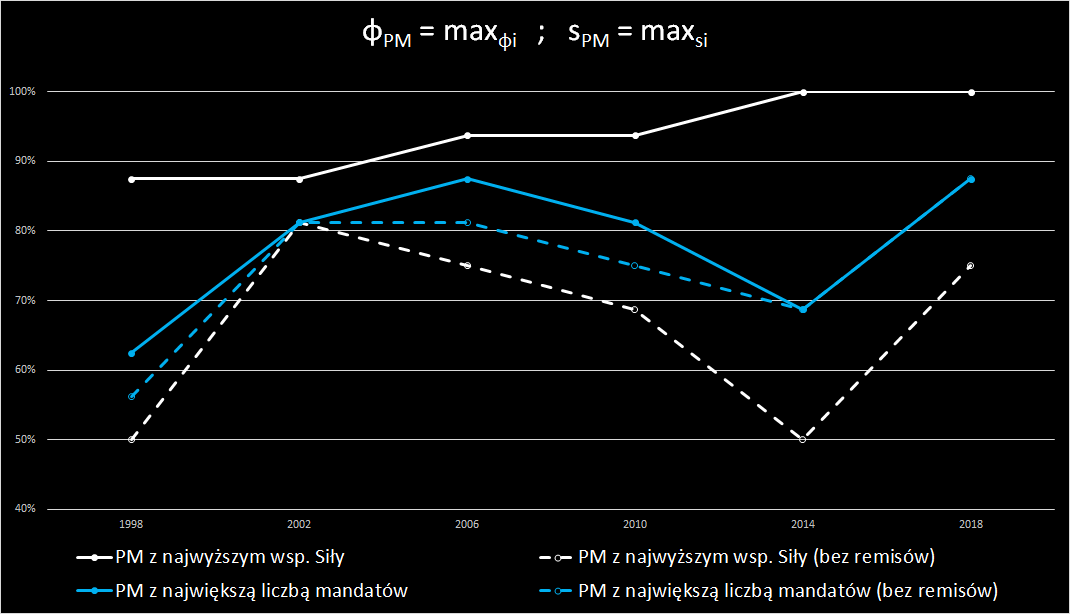
Częstość uzyskiwania przez PM najwyższej wartości indeksu siły/najwyższej liczby mandatów
Częstość PM z najniższą wartością indeksu siły >0 oraz z najniższą liczbą mnadatów >0 [bez dyktatorów]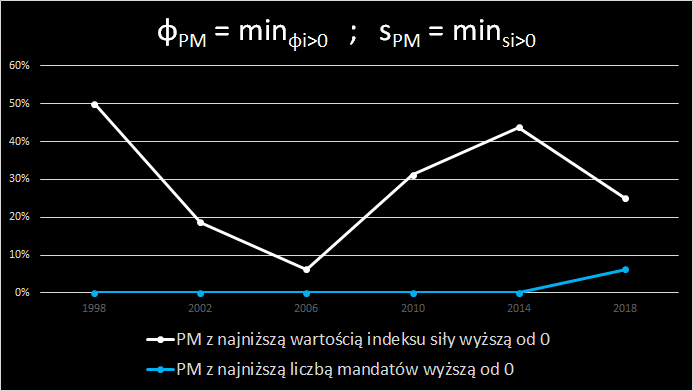
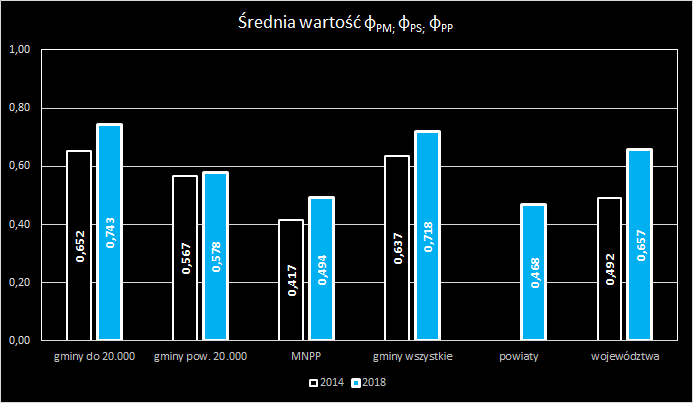
Porównanie wartości indeksu siły między typami JST
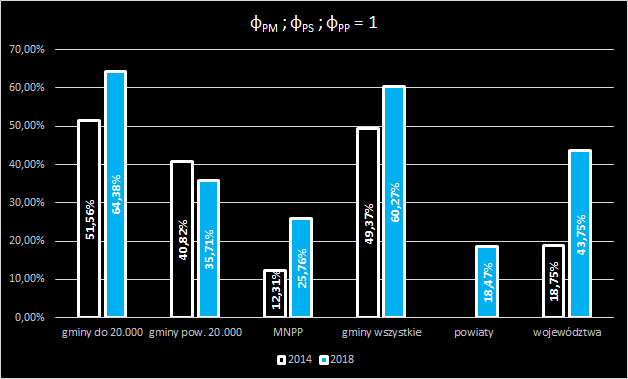
Partia Marszałkowska (starosty, prezydencka) z pozycją dyktatora
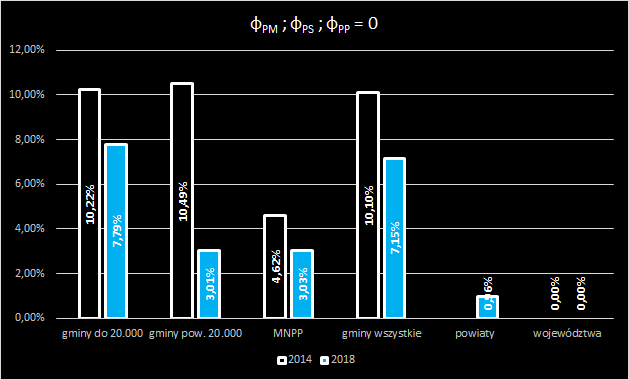
Partia Marszałkowska (starosty, prezydencka) z pozycją nieistotną
Junior Partnerzy w zarządach województw

Junior Partnerzy w zarządach województw
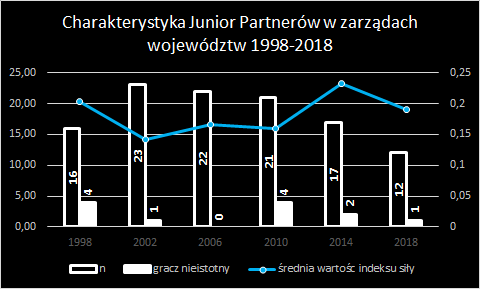
Junior Partnerzy w zarządach województw

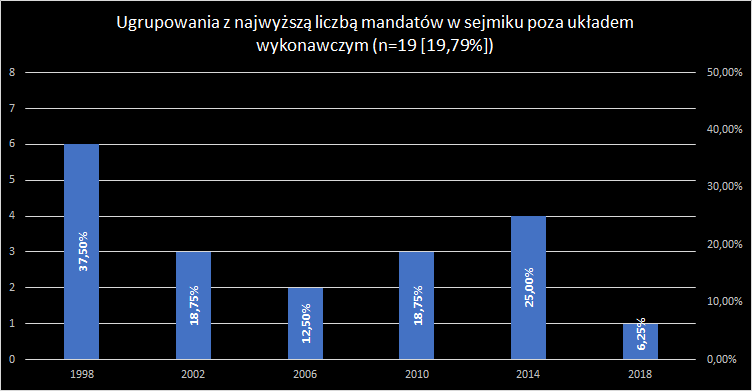
Zarząd bez udziału najsilniej reprezentowanego ugrupowania w sejmiku
Remisy: 1 x 1998, 2006, 2010.
Model rywalizacji o władzę wykonawczą w Sejmikach Województw od roku 1998
By Maciej Onasz
Model rywalizacji o władzę wykonawczą w Sejmikach Województw od roku 1998
- 106



