Przykład regresji liniowej

Eksperyment

Przeprowadzę regresje liniową dla testu kompresji plików tekstowych w 6 różnych formatach archiwalnych.

#E (doświadczenie)
120 testów kompresji

#T (klasa zadań)
zdolność kompresji plików tekstowych różnych formatów (7z, tar.7z, tar.gz, tar.bz2, rar, zip)

#P (miara wykonania)
wynik poziomu kompresji w procentach

Dane treningowe

Jest to zbiór 120 testów (po 20 na każdy format), podany w procentach. Zestaw został przygotowany pod RStudio.

  Wyniki testów:      Implementacja w R:

// 7z
(6.472531670704484,
7.578027313109487,
7.5228149350732565,
6.45737240370363,
6.744934095069766,
7.287350335624069,
6.638603103347123,
7.957382562570274,
7.501664312090725,
7.251015471294522,
6.070783191360533,
6.332054432015866,
6.542936322744936,
6.7174391322769225,
7.551883465144783,
6.5916645410470665,
7.77345856372267,
7.240904909092933,
7.468552193138748,
6.0522545971907675)


// tar.7z
(8.47014854173176,
 8.469591752858832,
 8.32320433028508,
 6.7731699286960065,
 6.577414469560608,
 7.1008982664207,
 8.088076115003787,
 6.859558362397365,
 6.85688993812073,
 8.373626408050768,
 7.399953040643595,
 7.6673942930065095,
 6.994650324108079,
 7.2052376959472895,
 6.808294803835452,
 7.224367644288577,
 8.839749389211647,
 7.293836411321536,
 6.864110736409202,
 8.485371760674752)

// tar.gz
(13.896328654140234,
 14.611641097813845,
 12.27013650443405,
 14.271163382567465,
 12.334800401702523,
 12.669181517325342,
 12.477508177049458,
 13.11292543914169,
 13.989539039321244,
 15.02637992799282,
 13.947708769701421,
 13.73510168120265,
 15.422181465663016,
 14.385912631638348,
 14.074038261547685,
 15.519078014418483,
 12.915294735692441,
 15.524328680709004,
 15.236410374753177,
 13.066102446056902)

// tar.bz2
(8.40189579082653,
 9.531365411356091,
 9.473886175779626,
 8.147643571253866,
 9.152481598546728,
 8.99937528395094,
 8.487080379156396,
 8.9766360509675,
 9.10609505395405,
 10.15000993781723,
 9.419158524135128,
 8.201742378994823,
 9.698653790866956,
 10.240020976169035,
 10.04146338510327,
 8.831212744582444,
 10.228813452413306,
 8.592599083203822,
 9.741769968997687,
 10.82528098858893)

// rar
(17.156613539904356,
 17.868259865790606,
 17.69180918764323,
 16.44657534919679,
 16.73420527111739,
 18.877843569032848,
 16.348398425616324,
 15.514598042704165,
 17.381894377060235,
 15.643551365472376,
 17.845848855562508,
 17.40530695207417,
 18.86303707677871,
 17.12033484876156,
 17.077027027495205,
 16.36872972548008,
 17.473640590906143,
 18.976167750544846,
 17.399126525968313,
 16.02712374832481)

 // zip
 (18.526143342256546,
 18.156133512966335,
 19.681578375399113,
 18.372708884067833,
 16.445215625688434,
 19.43624761980027,
 19.13772129267454,
 17.59182528965175,
 16.960937341675162,
 17.040610671043396,
 18.072870620526373,
 17.139651759527624,
 16.431620303541422,
 17.69356209039688,
 18.689643044024706,
 18.607126021757722,
 19.05406040791422,
 16.627767919562757,
 19.1111178137362,
 17.0169460773468)

x=c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,
3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,
4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,
5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5)


y=c(6.472531670704484,7.578027313109487,7.5228149350732565,
6.45737240370363,6.744934095069766,7.287350335624069,6.638603103347123,
7.957382562570274,7.501664312090725,7.251015471294522,6.070783191360533,
6.332054432015866,6.542936322744936,6.7174391322769225,7.551883465144783,
6.5916645410470665,7.77345856372267,7.240904909092933,7.468552193138748,
6.0522545971907675,.47014854173176, 8.469591752858832, 8.32320433028508,
6.7731699286960065, 6.577414469560608, 7.1008982664207, 8.088076115003787, 
6.859558362397365, 6.85688993812073, 8.373626408050768, 7.399953040643595, 
7.6673942930065095, 6.994650324108079, 7.2052376959472895, 6.808294803835452, 
7.224367644288577, 8.839749389211647, 7.293836411321536, 6.864110736409202, 
8.485371760674752, 13.896328654140234, 14.611641097813845, 12.27013650443405, 
14.271163382567465, 12.334800401702523, 12.669181517325342, 12.477508177049458, 
13.11292543914169, 13.989539039321244, 15.02637992799282, 13.947708769701421, 
13.73510168120265, 15.422181465663016, 14.385912631638348, 14.074038261547685, 
15.519078014418483, 12.915294735692441, 15.524328680709004, 15.236410374753177, 
13.066102446056902, 8.40189579082653, 9.531365411356091, 9.473886175779626, 
8.147643571253866, 9.152481598546728, 8.99937528395094, 8.487080379156396, 
8.9766360509675, 9.10609505395405, 10.15000993781723, 9.419158524135128, 
8.201742378994823, 9.698653790866956, 10.240020976169035, 10.04146338510327, 
8.831212744582444, 10.228813452413306, 8.592599083203822, 9.741769968997687, 
10.82528098858893, 17.156613539904356, 17.868259865790606, 17.69180918764323, 
16.44657534919679, 16.73420527111739, 18.877843569032848, 16.348398425616324, 
15.514598042704165, 17.381894377060235, 15.643551365472376, 17.845848855562508, 
17.40530695207417, 18.86303707677871, 17.12033484876156, 17.077027027495205, 
16.36872972548008, 17.473640590906143, 18.976167750544846, 17.399126525968313, 
16.02712374832481, 18.526143342256546, 18.156133512966335, 19.681578375399113, 
18.372708884067833, 16.445215625688434, 19.43624761980027, 19.13772129267454, 
17.59182528965175, 16.960937341675162, 17.040610671043396, 18.072870620526373, 
17.139651759527624, 16.431620303541422, 17.69356209039688, 18.689643044024706, 
18.607126021757722, 19.05406040791422, 16.627767919562757, 19.1111178137362, 
17.0169460773468)

Współczynnik regresji

Coefficients:

(Intercept)    x

  6.448      2.278

Residuals:
Min        1Q      Median     3Q       Max 
-5.135    -1.507    0.252    1.569    4.520

Coefficients:
                    Estimate Std.     Error      t value    Pr(>|t|)    
(Intercept)           6.4482          0.3854     16.73      <2e-16 ***
x                     2.2780          0.1273     17.89      <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.382 on 118 degrees of freedom
Multiple R-squared:  0.7307,    Adjusted R-squared:  0.7284 
F-statistic: 320.2 on 1 and 118 DF,  p-value: < 2.2e-16

Graf regresji liniowej

Gdzie:

0 - 7z

1 - tar.7z

2 - tar.gz

3 - tar.bz2

4 - rar

5 - zip

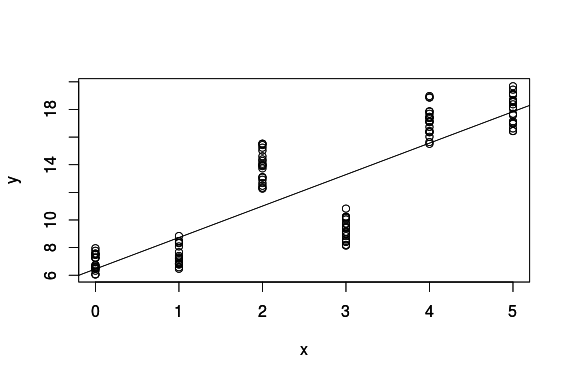
Rezultat testu:

Do obliczeń danych testowych użyta została funkcja test() z pakietu shapiro

shapiro.test(fit$residuals)

    Shapiro-Wilk normality test

data:  fit$residuals
W = 0.9714, p-value = 0.01156