Visualizing Deep Neural Network Decisions: Prediction Difference Analysis

LuisaMZintgraf, Taco S Cohen, Tameem Adel, MaxWelling

International Conference on Learning Representations 2017

University of Amsterdam, Canadian Institute of Advanced Research, Vrije Universiteit Brussel

15 Feb 2017

Goal

Visualize the response of a deep neural network to a specific input

Related Work

Two approaches for understanding DCNNs through visualization:

  • Find an input image that maximally activates a given node
    ⇒ visualize what the network is looking for
  • Visualize how the network responds to a specific input image
    ⇒ explain a particular classification made by the network

Related Work

Explaining Classifications for Individual Instances

Marko Robnik-Šikonja and Igor Kononenko,

Knowledge and Data Engineering, IEEE Transactions, 2008

Outline

Overview

Approach

Experiment

Conclusion & Future Work

Overview

  • A new, probabilistically sound methodology for explaining classification decisions made by DNN
  • Can be used to produce a saliency map for each instance, node pair
  • The map highlights the parts of the input that constitute most evidence for or against the activation of the given node

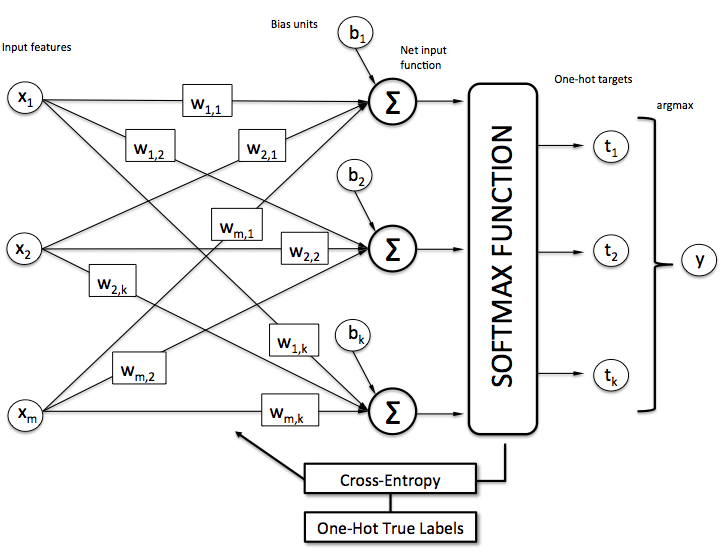
Approach

Prediction Difference Analysis

I
II
O
OO
I'
I′I'
O'
O′O'

1

0

1

1

1

0

 

1

p(c|\mathbf{x})
p(c∣x)p(c|\mathbf{x})
p(c|\mathbf{x}_{\backslash i})
p(c∣x\i)p(c|\mathbf{x}_{\backslash i})

Measure how the prediction changes if the feature is unknown


Define:

The probability of O=c given:

\mathbf{x}
x\mathbf{x}

all input features

all input features except

x_i
xix_i

Approach

Prediction Difference Analysis

x_i=p(c|\mathbf{x}) -p(c|\mathbf{x}_{\backslash i})
xi=p(c∣x)−p(c∣x\i)x_i=p(c|\mathbf{x}) -p(c|\mathbf{x}_{\backslash i})

Relevance of

             is easy to compute

How to compute                 ?

⇒ Simulate the absence of a feature by marginalizing the feature:

p(c|\mathbf{x})
p(c∣x)p(c|\mathbf{x})
p(c|\mathbf{x}_{\backslash i})
p(c∣x\i)p(c|\mathbf{x}_{\backslash i})
p(c|\mathbf{x}_{\backslash i})=\frac{p(c,\mathbf{x}_{\backslash i})}{p({\mathbf{x}_{\backslash i}})}=\sum_{x_i}\frac{p(c,\mathbf{x}_{\backslash i}, x_i)}{p({\mathbf{x}_{\backslash i}})}
p(c∣x\i)=p(c,x\i)p(x\i)=∑xip(c,x\i,xi)p(x\i)p(c|\mathbf{x}_{\backslash i})=\frac{p(c,\mathbf{x}_{\backslash i})}{p({\mathbf{x}_{\backslash i}})}=\sum_{x_i}\frac{p(c,\mathbf{x}_{\backslash i}, x_i)}{p({\mathbf{x}_{\backslash i}})}
=\sum_{x_i}\frac{p(c,\mathbf{x}_{\backslash i}, x_i)}{p({\mathbf{x}_{\backslash i}},x_i)}\frac{p({\mathbf{x}_{\backslash i}},x_i)}{p({\mathbf{x}_{\backslash i}})}=\sum_{x_i}p(x_i|\mathbf{x}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)
=∑xip(c,x\i,xi)p(x\i,xi)p(x\i,xi)p(x\i)=∑xip(xi∣x\i)p(c∣x\i,xi)=\sum_{x_i}\frac{p(c,\mathbf{x}_{\backslash i}, x_i)}{p({\mathbf{x}_{\backslash i}},x_i)}\frac{p({\mathbf{x}_{\backslash i}},x_i)}{p({\mathbf{x}_{\backslash i}})}=\sum_{x_i}p(x_i|\mathbf{x}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)

Approach

Prediction Difference Analysis

p(c|\mathbf{x}_{\backslash i})=\sum_{x_i}p(x_i|\mathbf{x}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)
p(c∣x\i)=∑xip(xi∣x\i)p(c∣x\i,xi)p(c|\mathbf{x}_{\backslash i})=\sum_{x_i}p(x_i|\mathbf{x}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)

How about                  ? It's infeasible with a large number of features

Assume that      is independent of        :

p(x_i|\mathbf{x}_{\backslash i})
p(xi∣x\i)p(x_i|\mathbf{x}_{\backslash i})
x_i
xix_i
\mathbf{x}_{\backslash i}
x\i\mathbf{x}_{\backslash i}
p(c|\mathbf{x}_{\backslash i})\approx \sum_{x_i}p(x_i)p(c|\mathbf{x}_{\backslash i}, x_i)
p(c∣x\i)≈∑xip(xi)p(c∣x\i,xi)p(c|\mathbf{x}_{\backslash i})\approx \sum_{x_i}p(x_i)p(c|\mathbf{x}_{\backslash i}, x_i)

is usually approximated by the empirical distribution

(However, an image is not the case)

p(x_i)
p(xi)p(x_i)

Approach

Prediction Difference Analysis

To compare              with               , we define

Weight of evidence:

\textrm{WE}_i(c|\mathbf{x})=\log_2 (odds(c|\mathbf{x}))- \log_2 (odds(c|\mathbf{x}_{\backslash i}))
WEi(c∣x)=log2(odds(c∣x))−log2(odds(c∣x\i))\textrm{WE}_i(c|\mathbf{x})=\log_2 (odds(c|\mathbf{x}))- \log_2 (odds(c|\mathbf{x}_{\backslash i}))
p(c|\mathbf{x}_{\backslash i})
p(c∣x\i)p(c|\mathbf{x}_{\backslash i})
p(c|\mathbf{x})
p(c∣x)p(c|\mathbf{x})
odds(c|\mathbf{x})=\frac{p(c|\mathbf{x})}{1-p(c|\mathbf{x})}
odds(c∣x)=p(c∣x)1−p(c∣x)odds(c|\mathbf{x})=\frac{p(c|\mathbf{x})}{1-p(c|\mathbf{x})}
\log_2 (odds(p))
log2(odds(p))\log_2 (odds(p))
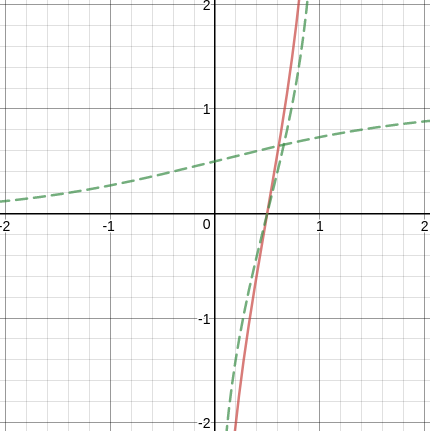
is similar to the inverse of sigmoid function

Avoid 0 probabilities

⇒ Laplace correction:

p \leftarrow \frac{(pN+1)}{N+K}
p←(pN+1)N+Kp \leftarrow \frac{(pN+1)}{N+K}

N: number of training instances

K: number of classes

where

Approach

Prediction Difference Analysis

\textrm{WE}_i(c|\mathbf{x})=\log_2 (odds(c|\mathbf{x}))- \log_2 (odds(c|\mathbf{x}_{\backslash i}))
WEi(c∣x)=log2(odds(c∣x))−log2(odds(c∣x\i))\textrm{WE}_i(c|\mathbf{x})=\log_2 (odds(c|\mathbf{x}))- \log_2 (odds(c|\mathbf{x}_{\backslash i}))

Positive value:

The feature contributes evidence for the class of interest

⇒ removing it would decrease the confidence of the classifier in the given class

Negative value:

The feature displays evidence against the class

⇒ removing it also removes potentially conflicting or irritating information and the classifier becomes more certain in the investigated class

The feature means    of this specific input
x_i
xix_i
know all the feature 
know all the features except
x_i
xix_i

Approach

Conditional Sampling

A pixel’s value is highly dependent on other pixels

p(x_i|\mathbf{x}_{\backslash i}) \neq p(x_i)
p(xi∣x\i)≠p(xi)p(x_i|\mathbf{x}_{\backslash i}) \neq p(x_i)

Two observations:

  • A pixel depends most strongly on a small neighborhood around it
  • the conditional of a pixel given its neighborhood does not depend on the position of the pixel in the image

Approach

Conditional Sampling

For a pixel     , we can find a patch      of size           that contains     , and condition on the remaining pixels        in that patch:

p(x_i|\mathbf{x}_{\backslash i}) \approx p(x_i|\hat{\mathbf{x}}_{\backslash i})
p(xi∣x\i)≈p(xi∣x^\i)p(x_i|\mathbf{x}_{\backslash i}) \approx p(x_i|\hat{\mathbf{x}}_{\backslash i})
x_i
xix_i
\hat{\mathbf{x}}_{\backslash i}
x^\i\hat{\mathbf{x}}_{\backslash i}
l
ll
l
ll
x_i
xix_i
\hat{\mathbf{x}}_{\backslash i}
x^\i\hat{\mathbf{x}}_{\backslash i}
\hat{\mathbf{x}}_{i}
x^i\hat{\mathbf{x}}_{i}
l \times l
l×ll \times l
x_i
xix_i

For a feature to become relevant, it now has to satisfy two conditions:

  • Be relevant to predict the class of interest
  • Be hard to predict from the neighboring pixels
\uparrow \text{probDiff}_i = p(c|\mathbf{x})-\sum_{x_i}p(x_i|\hat{\mathbf{x}}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)
↑probDiffi=p(c∣x)−∑xip(xi∣x^\i)p(c∣x\i,xi)\uparrow \text{probDiff}_i = p(c|\mathbf{x})-\sum_{x_i}p(x_i|\hat{\mathbf{x}}_{\backslash i})p(c|\mathbf{x}_{\backslash i}, x_i)

Approach

Multivariate Analysis

We expect that a neural network is relatively robust to just one feature of a high-dimensional input being unknown

⇒ remove several features at once:

k \times k
k×kk \times k
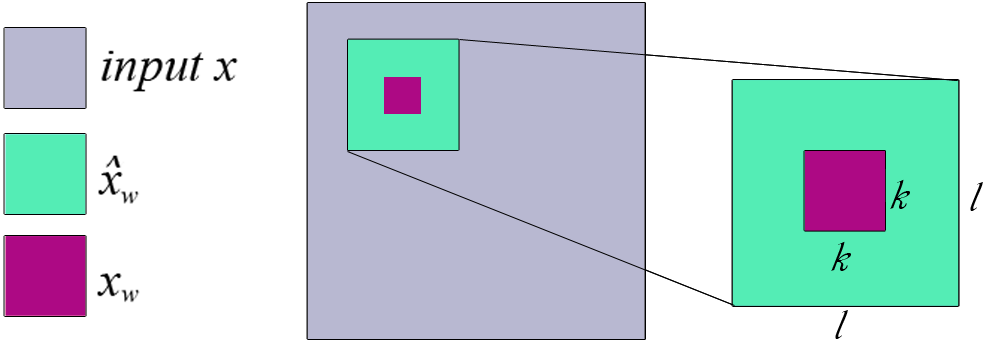
  • Do in a sliding window fashion

  • Take the average WE, which is accumulated in the pixel in the overlapping patches

Remove a             patch and calculate WEs of pixels in this patch

Approach

Deep Visualization of Hidden Layers

g(z|\mathbf{h}_{\backslash i}) \equiv \mathbb{E}_{p(h_i|\mathbf{h}_{\backslash i})}[z(\mathbf{h})]=\sum_{h_i}p(h_i|\mathbf{h}_{\backslash i})z(\mathbf{h}_{\backslash i},h_i)
g(z∣h\i)≡Ep(hi∣h\i)[z(h)]=∑hip(hi∣h\i)z(h\i,hi)g(z|\mathbf{h}_{\backslash i}) \equiv \mathbb{E}_{p(h_i|\mathbf{h}_{\backslash i})}[z(\mathbf{h})]=\sum_{h_i}p(h_i|\mathbf{h}_{\backslash i})z(\mathbf{h}_{\backslash i},h_i)

We can adapt the method to see how the units of any layer of the network influence a node from a deeper layer

: the vector representation of the output values in a layer H

    : the value of a node that depends on 

\mathbf{h}
h\mathbf{h}
z(\mathbf{h})
z(h)z(\mathbf{h})
\mathbf{h}
h\mathbf{h}

We are not dealing with probabilities, so WE is not applicable

Instead, we use activation difference:

\textrm{AD}_i(z|\mathbf{h})=g(z|\mathbf{h})-g(z|\mathbf{h}_{\backslash i})
ADi(z∣h)=g(z∣h)−g(z∣h\i)\textrm{AD}_i(z|\mathbf{h})=g(z|\mathbf{h})-g(z|\mathbf{h}_{\backslash i})

Approach

Pseudocode

How to implement it?

Approach

Implementing Conditional Sampling

Idea:

Assume pixels in the patch is a multivariate normal distribution

Implement            :

l\times l
l×ll\times l
  1. Do statistics on pixels from patches in the training instances
    ⇒ compute the mean vector and the covariance matrix
  2. Build a multivariate normal model
  3. Simulate the sampling process from this model
p(\hat{\mathbf{x}}_{w})
p(x^w)p(\hat{\mathbf{x}}_{w})

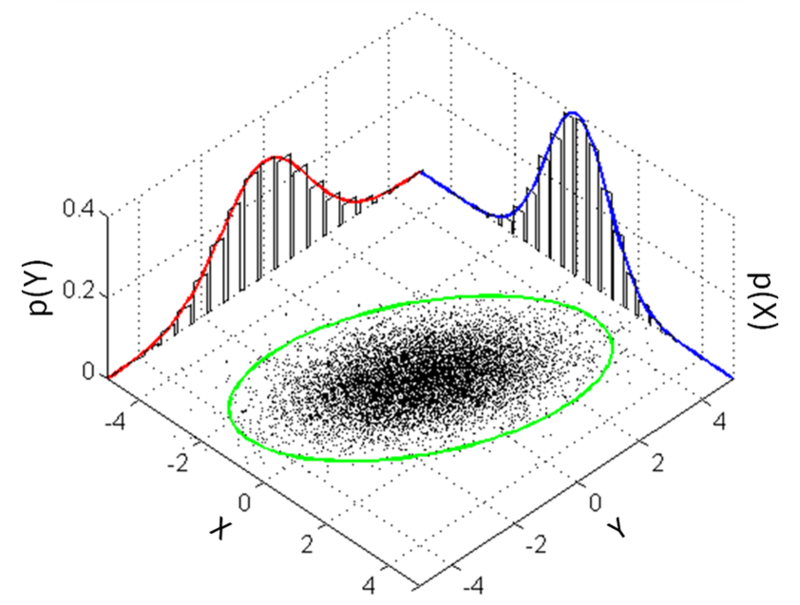
Approach

Implementing Conditional Sampling

But we want

⇒ conditional distribution of multivariate normal distribution

l\times l
l×ll\times l
p(\mathbf{x}_{w}|\hat{\mathbf{x}}_{w}\backslash \mathbf{x}_{w})
p(xw∣x^w\xw)p(\mathbf{x}_{w}|\hat{\mathbf{x}}_{w}\backslash \mathbf{x}_{w})
proof (an error in the formula of covariance matrix): http://fourier.eng.hmc.edu/e161/lectures/gaussianprocess/node7.html
\hat{\mathbf{x}}_{w}=\begin{bmatrix} \mathbf{x}_{w} \\ \hat{\mathbf{x}}_{w}\backslash \mathbf{x}_{w} \end{bmatrix} = \begin{bmatrix} \mathbf{x}_{1} \\ \mathbf{x}_{2} \end{bmatrix}
x^w=[xwx^w\xw]=[x1x2]\hat{\mathbf{x}}_{w}=\begin{bmatrix} \mathbf{x}_{w} \\ \hat{\mathbf{x}}_{w}\backslash \mathbf{x}_{w} \end{bmatrix} = \begin{bmatrix} \mathbf{x}_{1} \\ \mathbf{x}_{2} \end{bmatrix}
\mu=\begin{bmatrix} \mu_{1} \\ \mu_{2} \end{bmatrix}
μ=[μ1μ2]\mu=\begin{bmatrix} \mu_{1} \\ \mu_{2} \end{bmatrix}
\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12}\\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}
Σ=[Σ11Σ12Σ21Σ22]\Sigma=\begin{bmatrix} \Sigma_{11} & \Sigma_{12}\\ \Sigma_{21} & \Sigma_{22} \end{bmatrix}
\mu_{1|2}=\mu_1+\Sigma_{12}\Sigma_{22}^{-1}(\mathbf{x}_2-\mu_2)
μ1∣2=μ1+Σ12Σ22−1(x2−μ2)\mu_{1|2}=\mu_1+\Sigma_{12}\Sigma_{22}^{-1}(\mathbf{x}_2-\mu_2)
\Sigma_{1|2}=\Sigma_{11}+\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}
Σ1∣2=Σ11+Σ12Σ22−1Σ21\Sigma_{1|2}=\Sigma_{11}+\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}

Draw samples from distribution

\textrm{N}(\mu_{1|2}, \Sigma_{1|2})
N(μ1∣2,Σ1∣2)\textrm{N}(\mu_{1|2}, \Sigma_{1|2})

Experiment

 

Two parts:

  • ImageNet dataset, DCNNs
  • MRI scans, logistic regression classifier

Sampling method

  • Marginal sampling: empirical distribution
  • Conditional sampling: multivariate normal distribution
  • Draw only 10 samples
    (since no significant difference was observed with more samples)

Experiment

ImageNet: Understanding How a DCNN Makes Decisions

Use images from the ILSVRC challenge:

a large dataset of natural images from 1000 categories

 

Three DCNNs, use pre-trianed models, implemented by caffe
Analysis time:

  • AlexNet: 20 mins/image
  • GoogLeNet: 30 mins/image
  • 16-layer VGG Net: 70 mins/image

Experiment

Marginal v.s. Conditional Sampling

For the rest of our experiments, we show results using conditional sampling only

k=10,\ l=14 \ \textrm{GoogLeNet}
k=10, l=14 GoogLeNetk=10,\ l=14 \ \textrm{GoogLeNet}

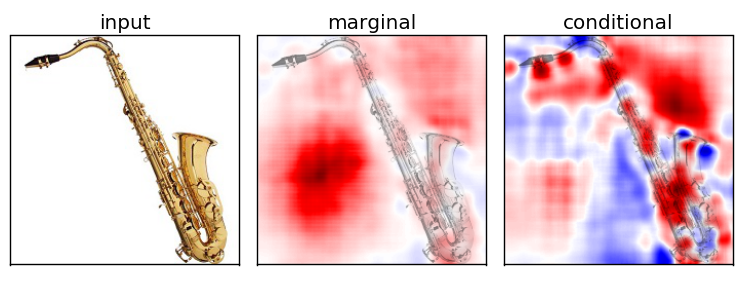
Experiment

Multivariate Analysis

k,\ l=k+4
k, l=k+4k,\ l=k+4

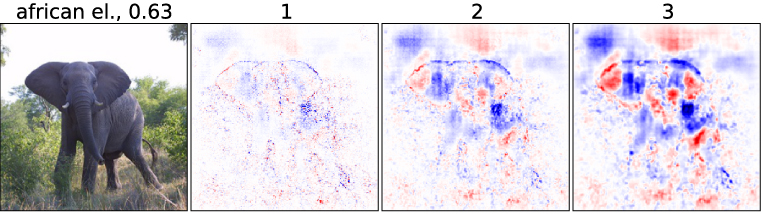
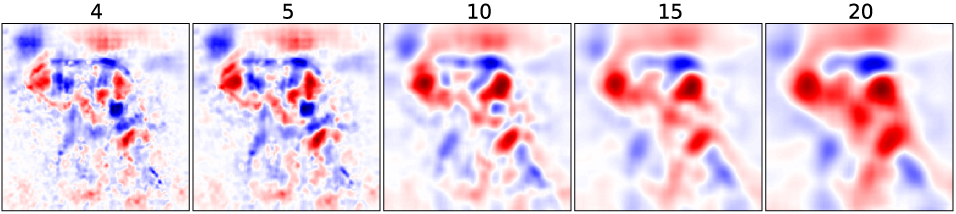
Experiment

Comparison with Sensitivity Map

  • top 5% relevant pixels by the absolute value (in a boolean mask)
  • k=1, l=5
  • highest scoring class in the penultimate layer

Experiment

Comparison with Sensitivity Map

Experiment

Deep Visualization of Hidden Network Layers

For each feature map in a convolutional layer:

  • First, compute the relevance of the input image for each hidden unit in that map
  • To estimate what the feature map as a whole is doing, we show the average of the relevance vectors over all units in that feature map

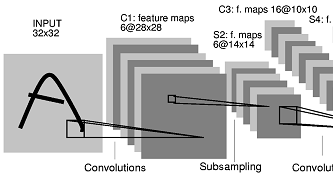
Experiment

Deep Visualization of Hidden Network Layers

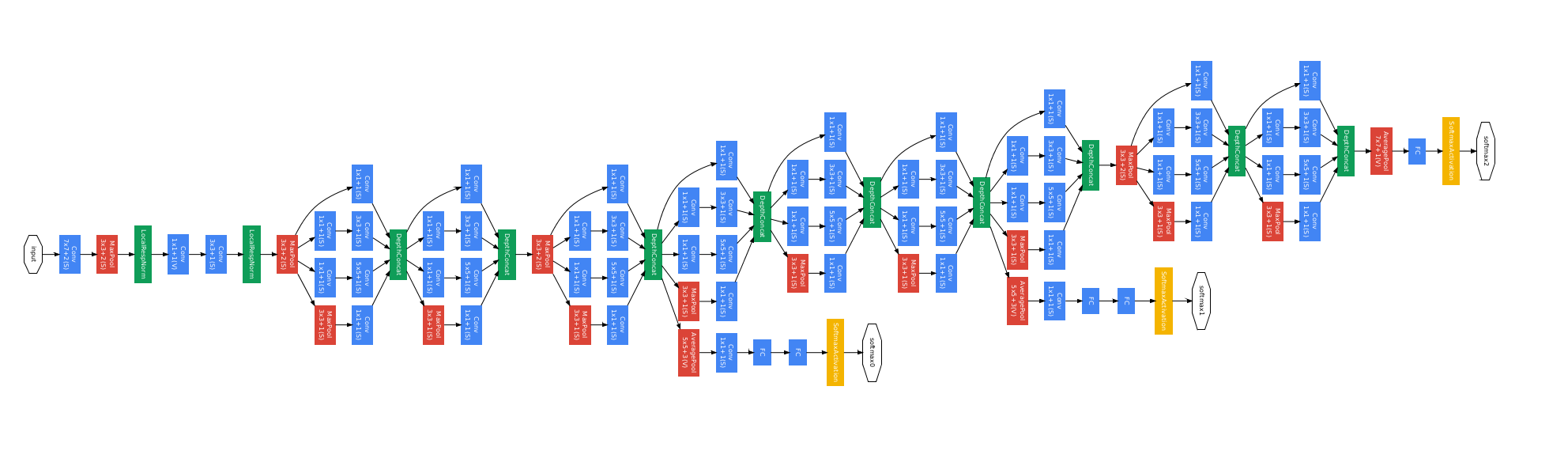
Simple image filters

Experiment

Deep Visualization of Hidden Network Layers

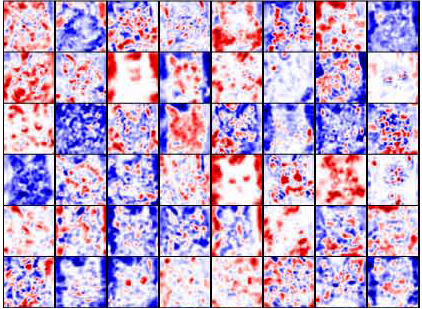
specialized to higher level features

Experiment

Deep Visualization of Hidden Network Layers

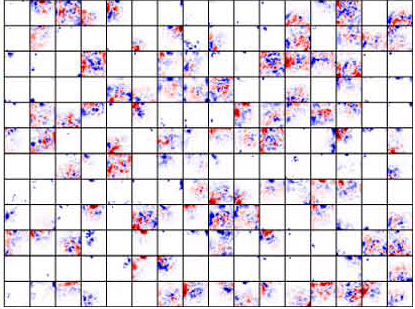
units are highly specialized

Experiment

Deep Visualization of Hidden Network Layers

Same layer, different input image

Experiment

Penultimate v.s. Output Layer

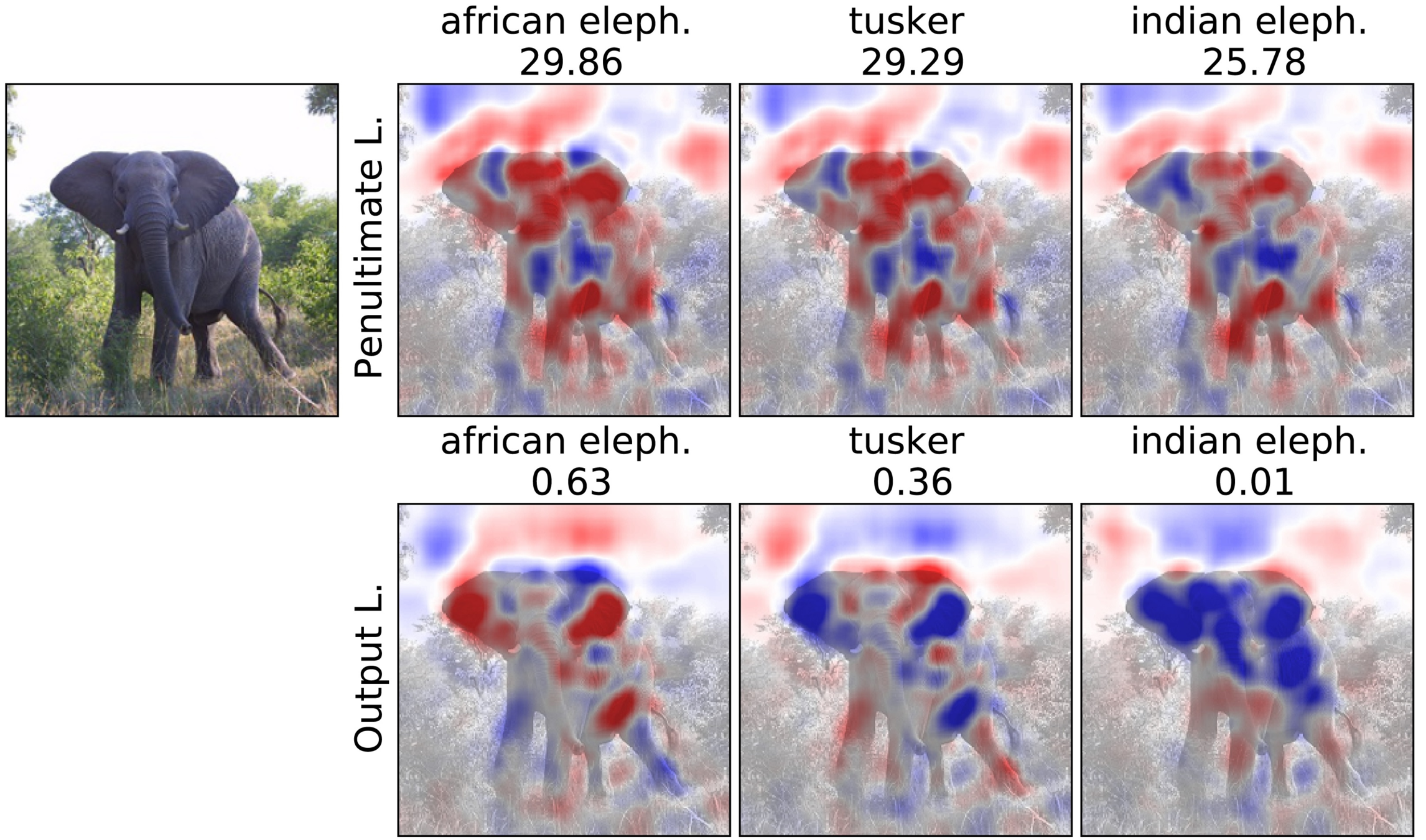
Experiment

Penultimate v.s. Output Layer

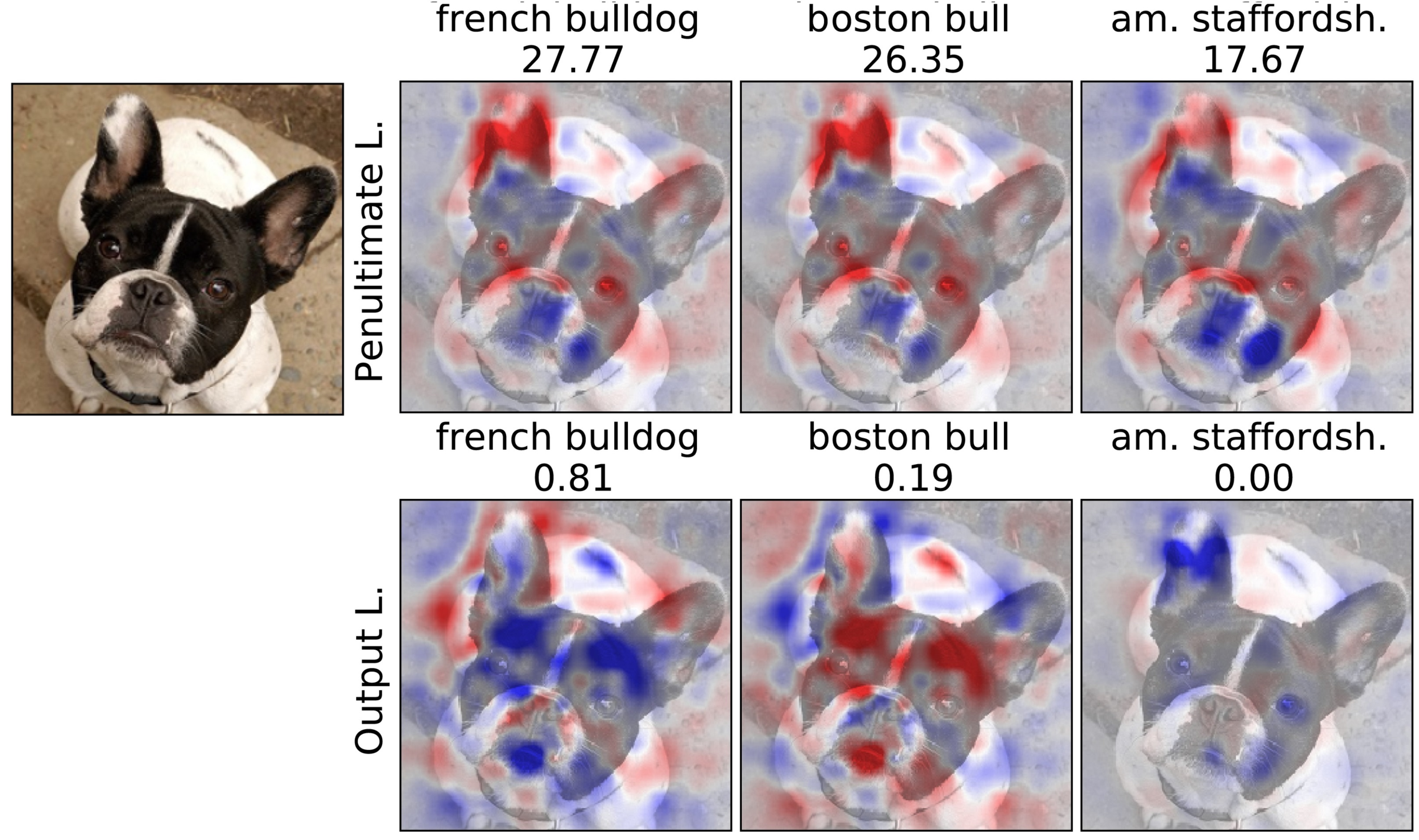
Experiment

Network Comparison

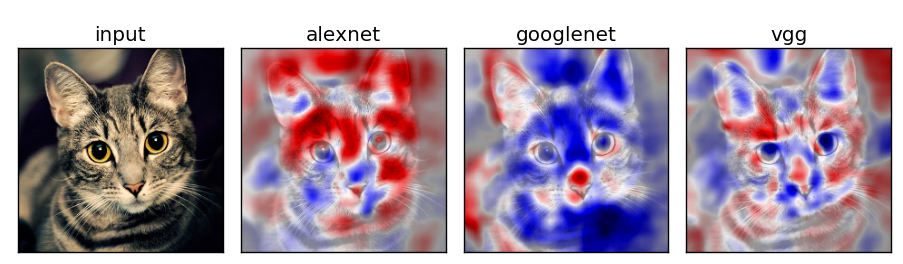
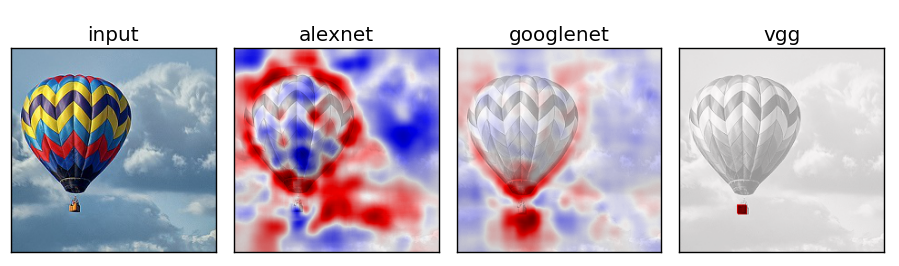
Experiment

MRI Data: Explaining Classifier Decisions in Medical Imaging

When classifying a patient, the practitioner weigh this information and incorporate it into the overall diagnosis process

MRI dataset of HIV and healthy patients

  • COBRA dataset: 3D MRIs from 100 HIV / 70 healthy individuals
  • Preprocessing ⇒ Fractional Anisotropy (FA) maps
  • Train on slices 29-40, first 70 samples of the HIV classes

L2-regularized Logistic Regression classifier (model details unknown)

  • k=3, l=7, adding location information
  • 69.3% accuracy in 10-fold cross-validation
  • 1.5 hrs/image analysis

Experiment

MRI Data: Explaining Classifier Decisions in Medical Imaging

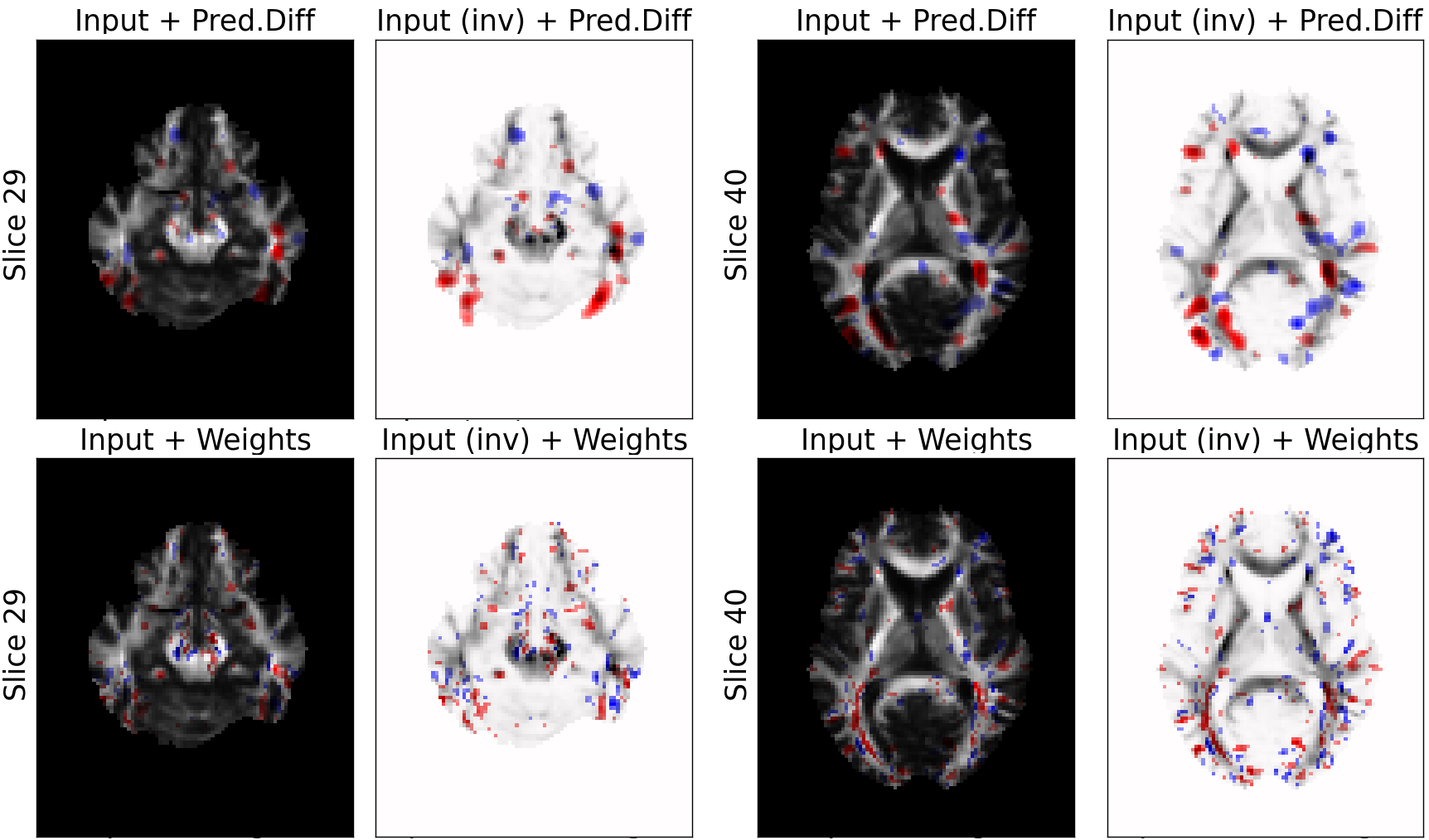
weights of the logistic regression classifier

(noisier, scattered)

prediction difference

Relevance values are shown only for voxels with value above 15% of the absolute maximum value

Experiment

MRI Data: Explaining Classifier Decisions in Medical Imaging

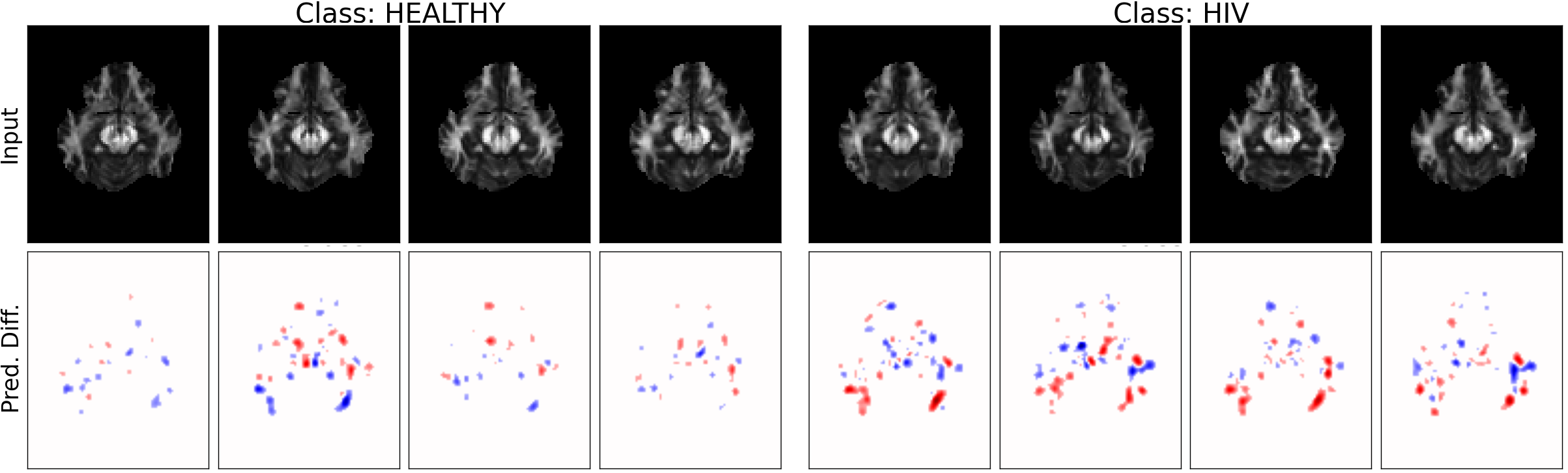
Different class

Experiment

MRI Data: Explaining Classifier Decisions in Medical Imaging

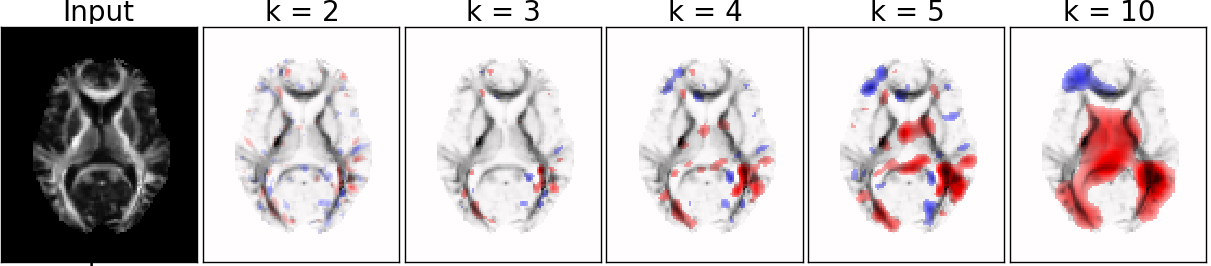
Different patch size

Conclusion & Future Work

Future work

  • Try to improve                                            by taking more image information
  • Make the method applicable for clinical analysis and practice
    a better classification algorithm is required
  • An interactive 3D visualization model will improve the usability of the system​

Contributions

  • Conditional sampling
  • Multivariate analysis
  • Deep visualization
p(x_i|\mathbf{x}_{\backslash i}) \approx p(x_i|\hat{\mathbf{x}}_{\backslash i})
p(xi∣x\i)≈p(xi∣x^\i)p(x_i|\mathbf{x}_{\backslash i}) \approx p(x_i|\hat{\mathbf{x}}_{\backslash i})

Visualizing Deep Neural Network Decisions: Prediction Difference Analysis

By Maeglin Liao

Made with Slides.com

Visualizing Deep Neural Network Decisions: Prediction Difference Analysis

  • 216

More from Maeglin Liao