Video Frame Synthesis using Deep Voxel Flow

Ziwei Liu, Xiaoou Tang, Raymond Yeh, Yiming Liu, Aseem Agarwala

The Chinese University of Hong Kong, University of Illinois at Urbana-Champaign, Google Inc.

 

2017, Feb 8

Goal

Frame Interpolation/Extrapolation

Application

  • Slow-motion effect
  • Increase frame rate

Optical Flow

(\Delta x,\Delta y)
(Δx,Δy)(\Delta x,\Delta y)

compute flow

on each pixel

Related Work

CNN Approach

  • Predict optical flow

Traditional Approach

  • Estimate optical flow between frames
  • Interpolate optical flow vector

⇒ Optical flow must be accurate

​⇒ Require supervision (flow ground-truth)

  • Directly hallucinate RGB pixel values

​⇒ Blurry

Outline

Overview

Formulation

Refinement and Extension

Experiment

Summary

Overview

Deep Voxel Flow

Combine the strengths of traditional and CNN approaches

  1. CNN ⇒ voxel flow
  2. Volume sampling layer(blending) ⇒ synthesized frame
  3. Synthesized frame ⇔ ground-truth frame
*voxel=volume pixel=3D pixel

End-to-end trained deep network

No FC layer ⇒ any resolution

Quantitatively and qualitatively improve upon the state-of-the-art

Formulation

Architecture
Y\in \mathbb{R} ^{H\times W}
Y∈RH×WY\in \mathbb{R} ^{H\times W}
X\in \mathbb{R} ^{H\times W\times L}
X∈RH×W×LX\in \mathbb{R} ^{H\times W\times L}

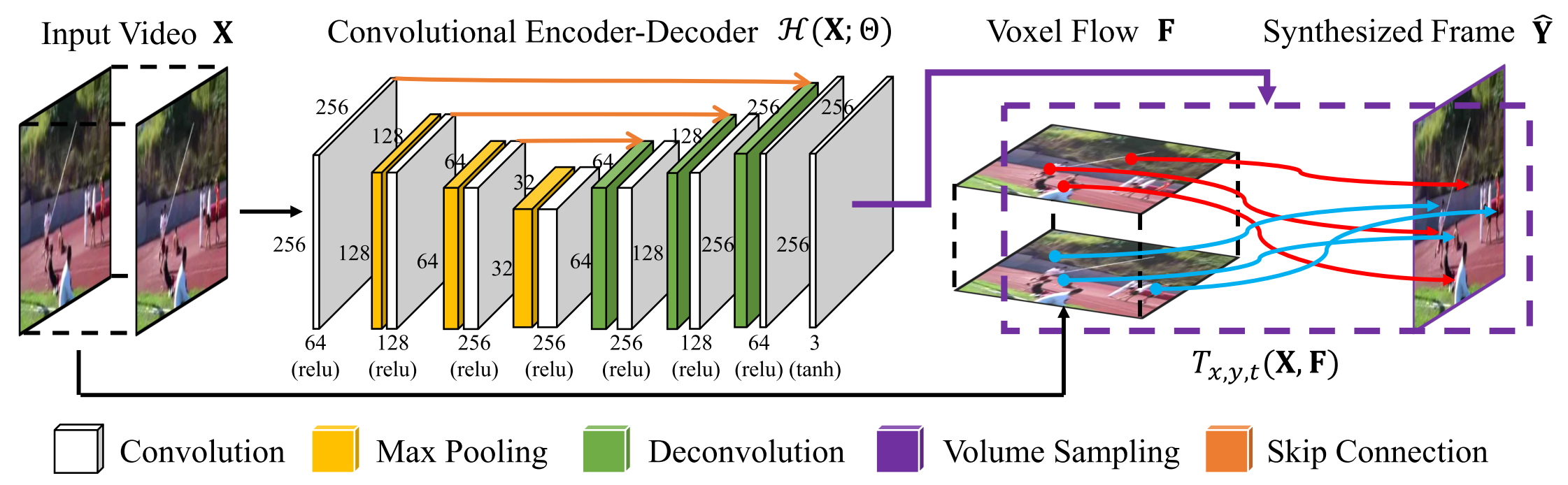
Input frames

Target frame

\hat{Y}\in \mathbb{R} ^{H\times W}
Y^∈RH×W\hat{Y}\in \mathbb{R} ^{H\times W}

Synthesized frame

F=\mathcal{H}\left( X;\Theta \right) =(\Delta x,\Delta y,\Delta t)
F=H(X;Θ)=(Δx,Δy,Δt)F=\mathcal{H}\left( X;\Theta \right) =(\Delta x,\Delta y,\Delta t)

Formulation

CNN ⇒ Voxel Flow

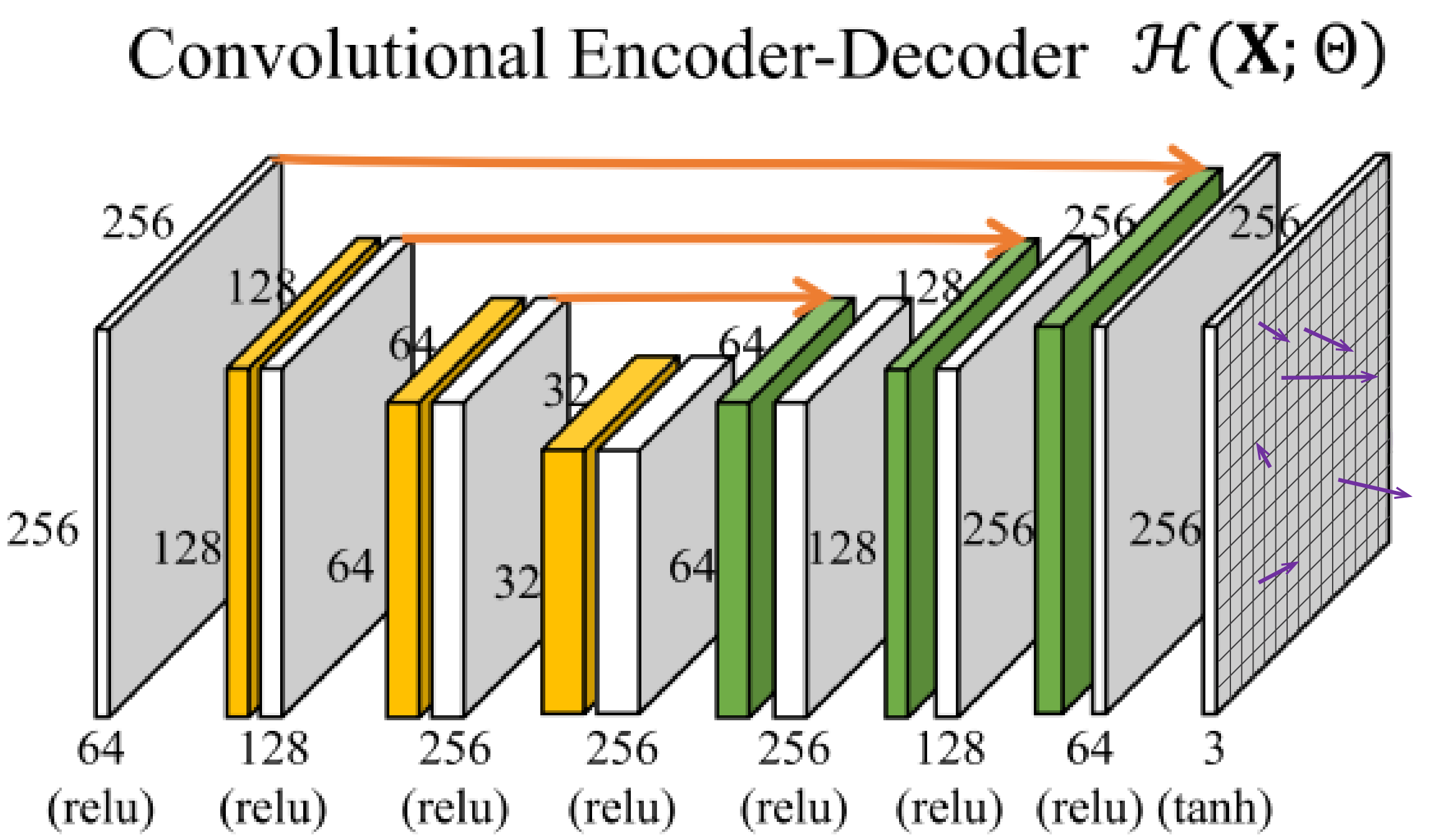
Predict the voxel flow on every pixel of

\Theta
Θ\Theta

network parameters

Voxel Flow

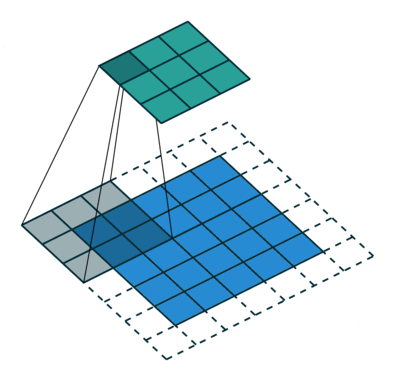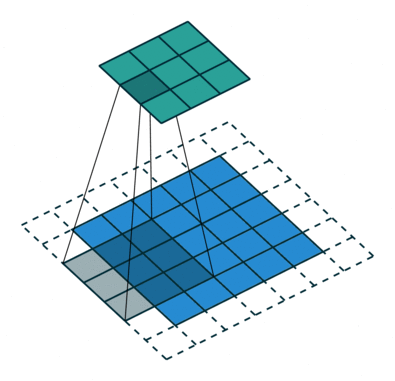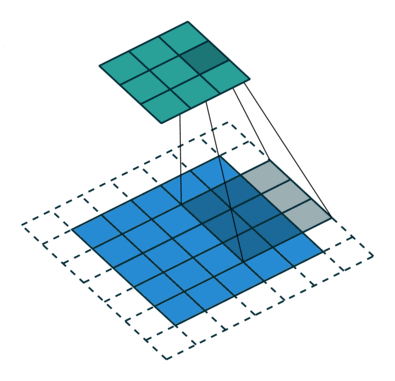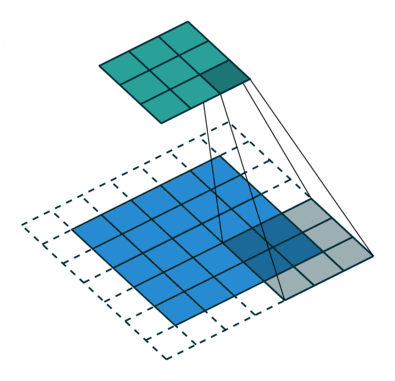
*Deconvolution

kernel sizes:

5x5, 5x5, 3x3, 3x3, 3x3, 5x5, 5x5

F_{motion}=(\Delta x, \Delta y)
Fmotion=(Δx,Δy)F_{motion}=(\Delta x, \Delta y)
F_{mask}=(\Delta t)
Fmask=(Δt)F_{mask}=(\Delta t)
\hat{Y}
Y^\hat{Y}
\Delta x, \Delta y, \Delta t \in (-1, 1)
Δx,Δy,Δt∈(−1,1)\Delta x, \Delta y, \Delta t \in (-1, 1)
\Delta t \in (0, 1)
Δt∈(0,1)\Delta t \in (0, 1)

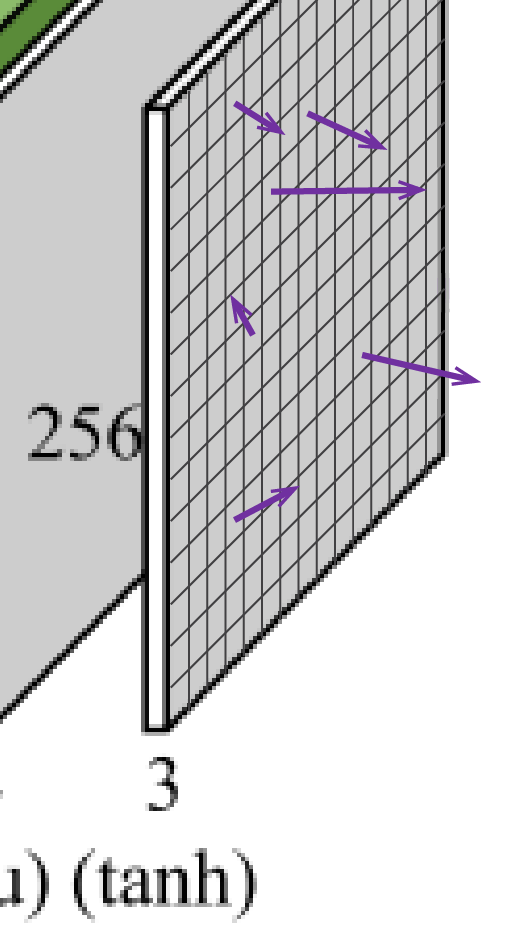
it should be:

Formulation

Volume Sampling Layer ⇒ Synthesized Frame
F_{motion}=(\Delta x, \Delta y)
Fmotion=(Δx,Δy)F_{motion}=(\Delta x, \Delta y)
F_{mask}=(\Delta t)
Fmask=(Δt)F_{mask}=(\Delta t)

Assume optical flow is temporally symmetric around the in-between frame

Corresponding locations in:

  • Previous frame
  • Next frame
L^0=(x-\Delta x, y-\Delta y)
L0=(x−Δx,y−Δy)L^0=(x-\Delta x, y-\Delta y)
L^1=(x+\Delta x, y+\Delta y)
L1=(x+Δx,y+Δy)L^1=(x+\Delta x, y+\Delta y)
*(x,y):pixel location in the synthesized frame

Linear blending weight between the previous and next frames

Formulation

Volume Sampling Layer ⇒ Synthesized Frame
F_{motion}
FmotionF_{motion}
F_{mask}
FmaskF_{mask}
Y
YY

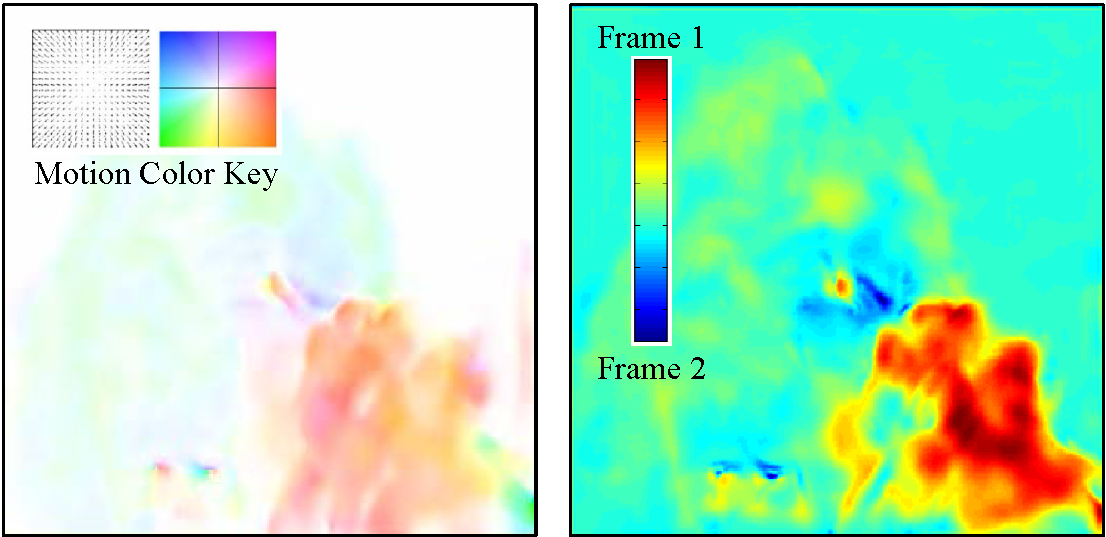
Formulation

Volume Sampling Layer ⇒ Synthesized Frame
\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)
Y^(x,y)=∑i,j,k∈[0,1]WijkX(Vijk)\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)

Trilinear interpolation

V^{000}=(\lfloor L^0_x\rfloor,\lfloor L^0_y \rfloor,0)
V000=(⌊Lx0⌋,⌊Ly0⌋,0)V^{000}=(\lfloor L^0_x\rfloor,\lfloor L^0_y \rfloor,0)
V^{100}=(\lceil L^0_x\rceil,\lfloor L^0_y \rfloor,0)
V100=(⌈Lx0⌉,⌊Ly0⌋,0)V^{100}=(\lceil L^0_x\rceil,\lfloor L^0_y \rfloor,0)
V^{011}=(\lfloor L^1_x\rfloor,\lceil L^1_y \rceil,1)
V011=(⌊Lx1⌋,⌈Ly1⌉,1)V^{011}=(\lfloor L^1_x\rfloor,\lceil L^1_y \rceil,1)
V^{111}=(\lceil L^1_x\rceil,\lceil L^1_y \rceil,1)
V111=(⌈Lx1⌉,⌈Ly1⌉,1)V^{111}=(\lceil L^1_x\rceil,\lceil L^1_y \rceil,1)
\ldots
…\ldots
W^{000}=(\lceil L^0_x\rceil-L^0_x)(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
W000=(⌈Lx0⌉−Lx0)(⌈Ly0⌉−Ly0)(1−Δt)W^{000}=(\lceil L^0_x\rceil-L^0_x)(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
W^{100}=(L^0_x-\lfloor L^0_x\rfloor)(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
W100=(Lx0−⌊Lx0⌋)(⌈Ly0⌉−Ly0)(1−Δt)W^{100}=(L^0_x-\lfloor L^0_x\rfloor)(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
W^{011}=(\lceil L^1_x\rceil-L^1_x)(L^1_y-\lfloor L^1_y \rfloor)\Delta t
W011=(⌈Lx1⌉−Lx1)(Ly1−⌊Ly1⌋)ΔtW^{011}=(\lceil L^1_x\rceil-L^1_x)(L^1_y-\lfloor L^1_y \rfloor)\Delta t
W^{111}=(L^1_x-\lfloor L^1_x\rfloor)(L^1_y-\lfloor L^1_y \rfloor)\Delta t
W111=(Lx1−⌊Lx1⌋)(Ly1−⌊Ly1⌋)ΔtW^{111}=(L^1_x-\lfloor L^1_x\rfloor)(L^1_y-\lfloor L^1_y \rfloor)\Delta t
\ldots
…\ldots

Volume Sampling Function

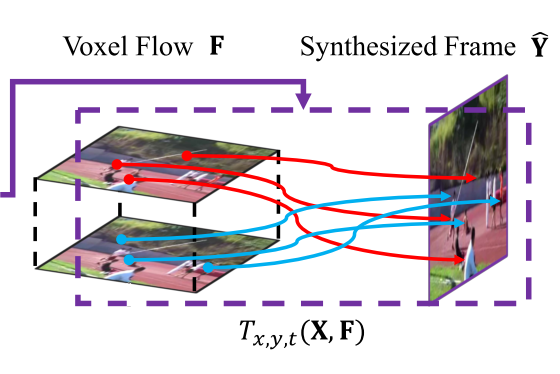
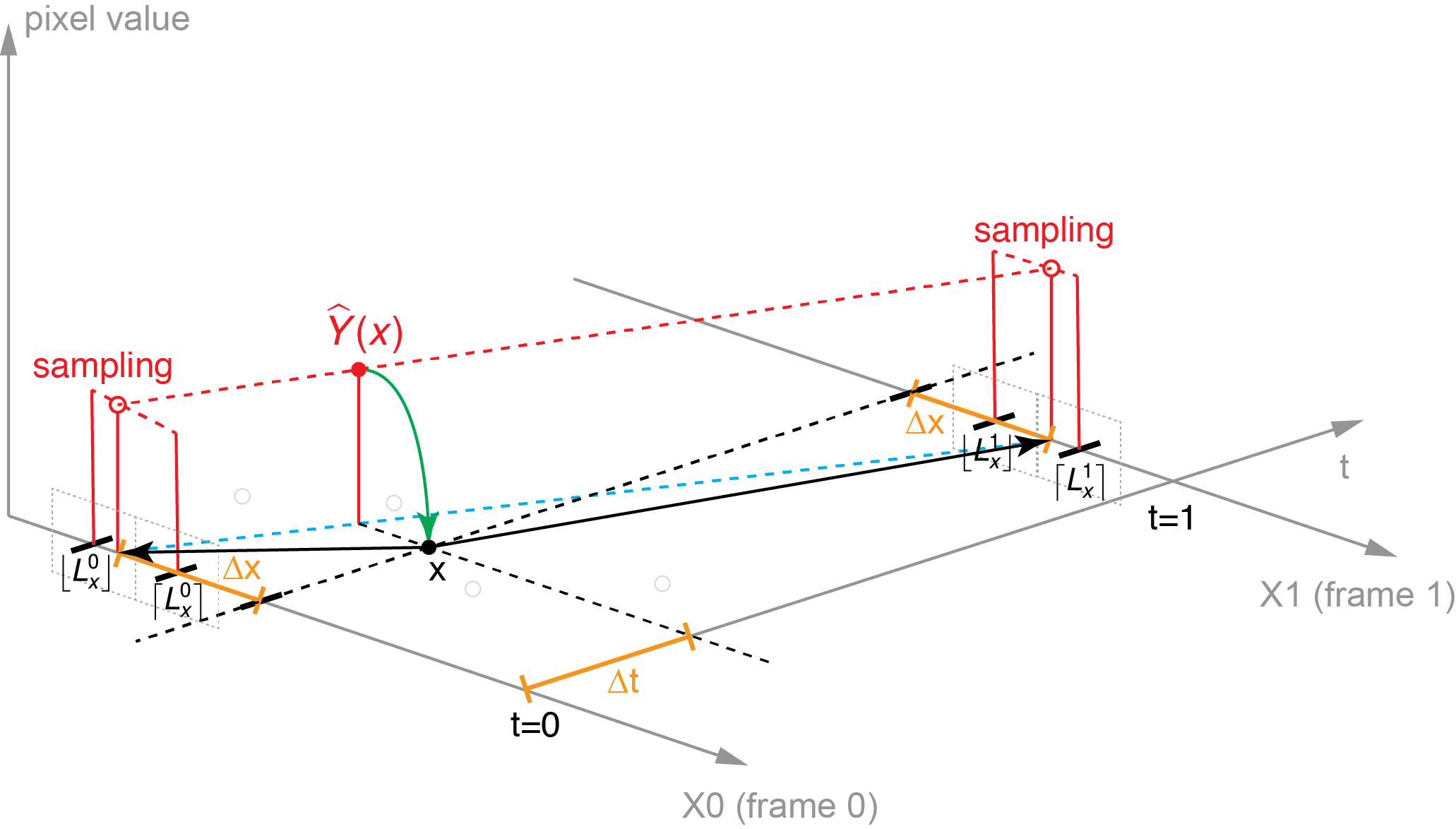
\mathcal{T}_{x,y,t}(X,\mathcal{H}\left( X;\Theta \right) )=\hat{Y}
Tx,y,t(X,H(X;Θ))=Y^\mathcal{T}_{x,y,t}(X,\mathcal{H}\left( X;\Theta \right) )=\hat{Y}

Formulation Visualization

Synthesize frame in 1D
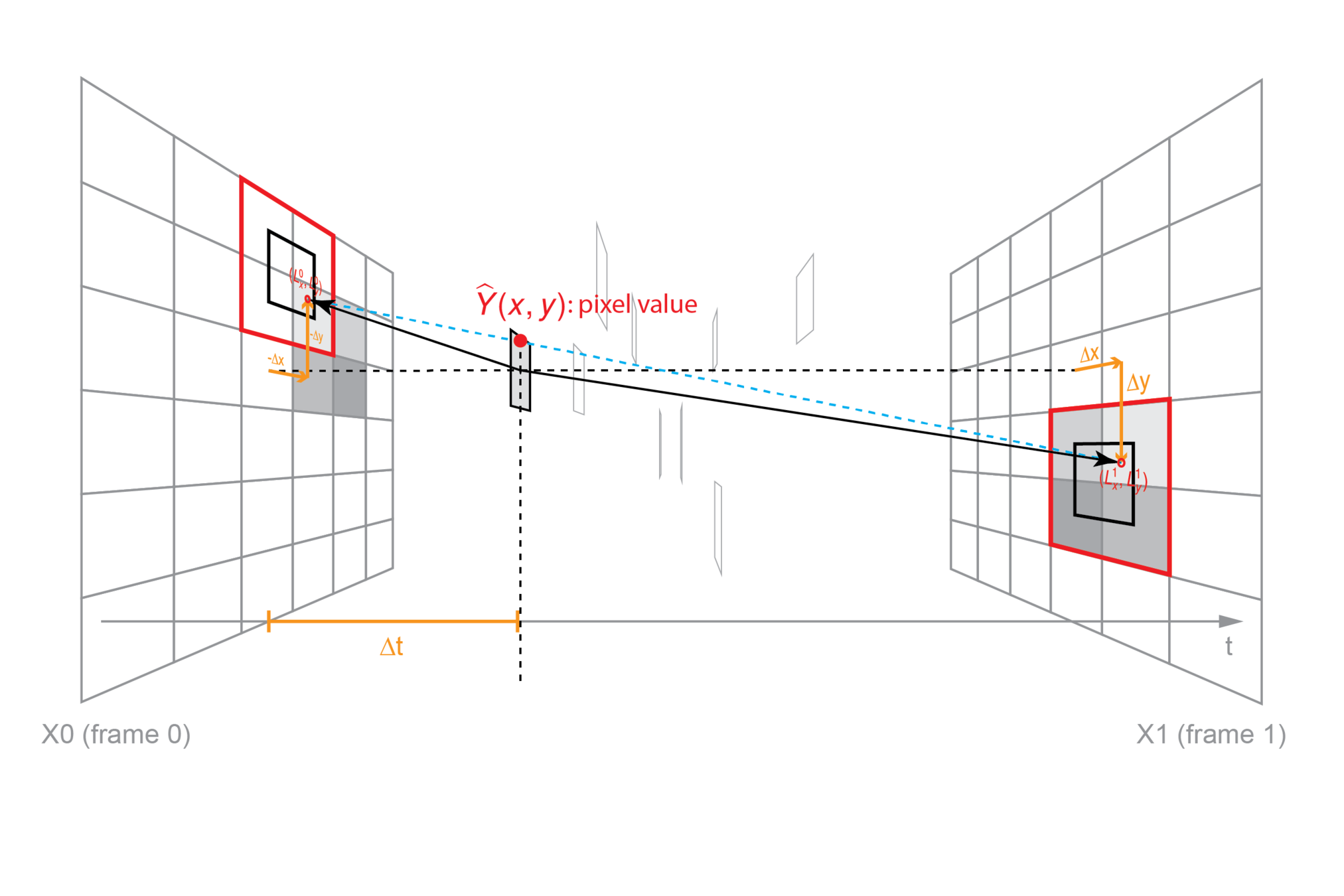
\hat{Y}(x)=\sum _{i,j\in \left[ 0,1\right] }W^{ij}X\left( V^{ij}\right)
Y^(x)=∑i,j∈[0,1]WijX(Vij)\hat{Y}(x)=\sum _{i,j\in \left[ 0,1\right] }W^{ij}X\left( V^{ij}\right)

Formulation Visualization

Synthesize frame in 2D
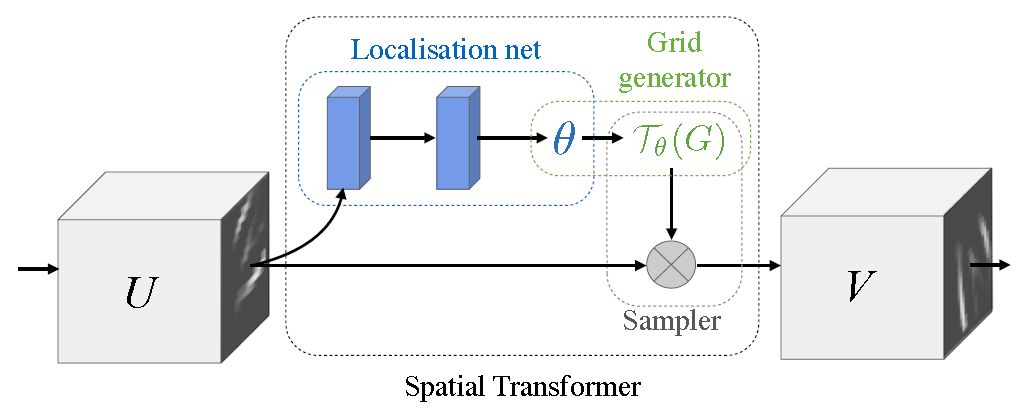
\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)
Y^(x,y)=∑i,j,k∈[0,1]WijkX(Vijk)\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)

Digression

Spatial Transformer Networks
DeepMind, 2015 NIPS, Cited by 222
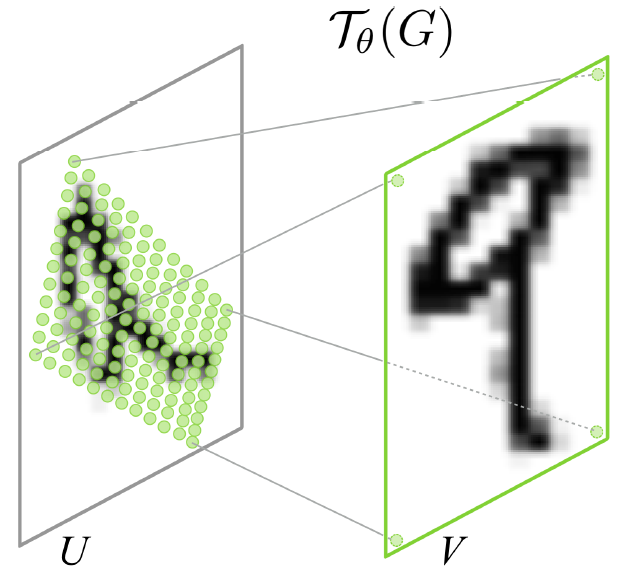
\begin{pmatrix} x^s_i\\ y^s_i \end{pmatrix}=\mathcal{T}_{\theta}(G_i)=\begin{bmatrix} \theta_{11} & \theta_{12} & \theta_{13}\\ \theta_{21} & \theta_{22} & \theta_{23} \end{bmatrix}\begin{pmatrix} x^t_i\\ y^t_i\\ 1 \end{pmatrix}
(xisyis)=Tθ(Gi)=[θ11θ12θ13θ21θ22θ23](xityit1)\begin{pmatrix} x^s_i\\ y^s_i \end{pmatrix}=\mathcal{T}_{\theta}(G_i)=\begin{bmatrix} \theta_{11} & \theta_{12} & \theta_{13}\\ \theta_{21} & \theta_{22} & \theta_{23} \end{bmatrix}\begin{pmatrix} x^t_i\\ y^t_i\\ 1 \end{pmatrix}

Formulation

Synthesized Frame ⇔ Ground-Truth Frame

Loss Function

\dfrac {1} {N}\sum _{\left\langle X,Y\right\rangle \in \mathcal{D}}\left(\left\| Y-\hat{Y} \right\| _{1} + \lambda _{1}\left\| \nabla F_{motion}\right\|_{1}+\lambda_{2}\left\| \nabla F_{mask}\right\|_{1}\right)
1N∑⟨X,Y⟩∈D(∥Y−Y^∥1+λ1∥∇Fmotion∥1+λ2∥∇Fmask∥1)\dfrac {1} {N}\sum _{\left\langle X,Y\right\rangle \in \mathcal{D}}\left(\left\| Y-\hat{Y} \right\| _{1} + \lambda _{1}\left\| \nabla F_{motion}\right\|_{1}+\lambda_{2}\left\| \nabla F_{mask}\right\|_{1}\right)

total variation:

\sum _{n}\left| x_{n+1}-x_{n}\right|
∑n∣xn+1−xn∣\sum _{n}\left| x_{n+1}-x_{n}\right|

L1 approximated by Charbonnier loss

{\Phi }\left( x\right) =\left( x^{2}+\epsilon ^{2}\right) ^{1 / 2}
Φ(x)=(x2+ϵ2)1/2{\Phi }\left( x\right) =\left( x^{2}+\epsilon ^{2}\right) ^{1 / 2}

Empirically

\lambda_1=0.01
λ1=0.01\lambda_1=0.01
\lambda_2=0.005
λ2=0.005\lambda_2=0.005
\epsilon=0.001
ϵ=0.001\epsilon=0.001

Learning settings

  • Batch size: 32
  • Batch normalization
  • Gaussian init:
  • ADAM solver:
\sigma=0.01
σ=0.01\sigma=0.01
lr=0.0001,\beta_1=0.9,\beta_2=0.999
lr=0.0001,β1=0.9,β2=0.999lr=0.0001,\beta_1=0.9,\beta_2=0.999

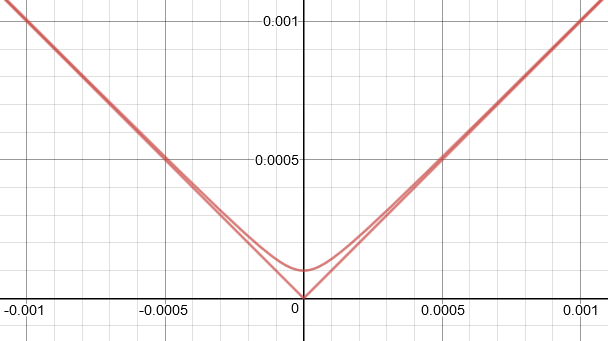
Formulation

End-to-end Fully Differentiable System
\dfrac {d\hat {Y}} {d\Theta }=\dfrac {d\hat {Y}} {dF}\dfrac {dF} {d\Theta }\ \Rightarrow \ \dfrac {\partial \hat {Y}\left( x,y \right) } {\partial \left( \Delta x\right) }=\sum _{i,j,k\in \left[ 0,1\right] }E^{ijk}X\left( V^{ijk}\right)
dY^dΘ=dY^dFdFdΘ ⇒ ∂Y^(x,y)∂(Δx)=∑i,j,k∈[0,1]EijkX(Vijk)\dfrac {d\hat {Y}} {d\Theta }=\dfrac {d\hat {Y}} {dF}\dfrac {dF} {d\Theta }\ \Rightarrow \ \dfrac {\partial \hat {Y}\left( x,y \right) } {\partial \left( \Delta x\right) }=\sum _{i,j,k\in \left[ 0,1\right] }E^{ijk}X\left( V^{ijk}\right)
=\sum _{t\in \left[ 0,1\right] }\sum _{m}^{W}\sum _{n}^{H}X_{mn}^{t}\left( 1-\left| \Delta t-t\right| \right) max(0,1-\left|L_{x}^{t}-m\right|)max(0,1-\left|L_{y}^{t}-n\right|)
=∑t∈[0,1]∑mW∑nHXmnt(1−∣Δt−t∣)max(0,1−∣Lxt−m∣)max(0,1−∣Lyt−n∣)=\sum _{t\in \left[ 0,1\right] }\sum _{m}^{W}\sum _{n}^{H}X_{mn}^{t}\left( 1-\left| \Delta t-t\right| \right) max(0,1-\left|L_{x}^{t}-m\right|)max(0,1-\left|L_{y}^{t}-n\right|)
\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)
Y^(x,y)=∑i,j,k∈[0,1]WijkX(Vijk)\hat{Y}(x,y)=\sum _{i,j,k\in \left[ 0,1\right] }W^{ijk}X\left( V^{ijk}\right)
E^{000}=-(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
E000=−(⌈Ly0⌉−Ly0)(1−Δt)E^{000}=-(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
E^{100}=(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
E100=(⌈Ly0⌉−Ly0)(1−Δt)E^{100}=(\lceil L^0_y\rceil-L^0_y)(1-\Delta t)
\ldots
…\ldots
E^{111}=(L^1_y-\lfloor L^1_y\rfloor)\Delta t
E111=(Ly1−⌊Ly1⌋)ΔtE^{111}=(L^1_y-\lfloor L^1_y\rfloor)\Delta t
E^{011}=-(L^1_y-\lfloor L^1_y\rfloor)\Delta t
E011=−(Ly1−⌊Ly1⌋)ΔtE^{011}=-(L^1_y-\lfloor L^1_y\rfloor)\Delta t

Note

Formulation Visualization

Another Formulation
\sum _{t\in \left[ 0,1\right] }\sum _{m}^{W}\sum _{n}^{H}X_{mn}^{t}\left( 1-\left| \Delta t-t\right| \right) max(0,1-\left|L_{x}^{t}-m\right|)max(0,1-\left|L_{y}^{t}-n\right|)
∑t∈[0,1]∑mW∑nHXmnt(1−∣Δt−t∣)max(0,1−∣Lxt−m∣)max(0,1−∣Lyt−n∣)\sum _{t\in \left[ 0,1\right] }\sum _{m}^{W}\sum _{n}^{H}X_{mn}^{t}\left( 1-\left| \Delta t-t\right| \right) max(0,1-\left|L_{x}^{t}-m\right|)max(0,1-\left|L_{y}^{t}-n\right|)

Refinement

Multi-scale Flow Fusion

Hard to find large motions that fall outside the kernel

\mathcal{H}_{N},\mathcal{H}_{N-1},\ldots,\mathcal{H}_{0}
HN,HN−1,…,H0\mathcal{H}_{N},\mathcal{H}_{N-1},\ldots,\mathcal{H}_{0}
s_{N},s_{N-1},\ldots,s_{0}
sN,sN−1,…,s0s_{N},s_{N-1},\ldots,s_{0}
s_{2}=64\times 64,s_{1}=128 \times 128,s_{0}=256 \times 256
s2=64×64,s1=128×128,s0=256×256s_{2}=64\times 64,s_{1}=128 \times 128,s_{0}=256 \times 256
F_k
FkF_k
F_{motion}
FmotionF_{motion}

Deal with large and small motions

  1. Mutiple encoder-decorders
    deal with different scales                              , coarse ⇒ fine
    e.g.
  2. Predict voxel flow       at that resolution
  3. Upsample and concatenate, only              is retained
  4. Further convolute (      ) on the fused flow fields ⇒
F_{0}
F0F_{0}
\mathcal{H}_{0}
H0\mathcal{H}_{0}

Refinement

Multi-scale Flow Fusion
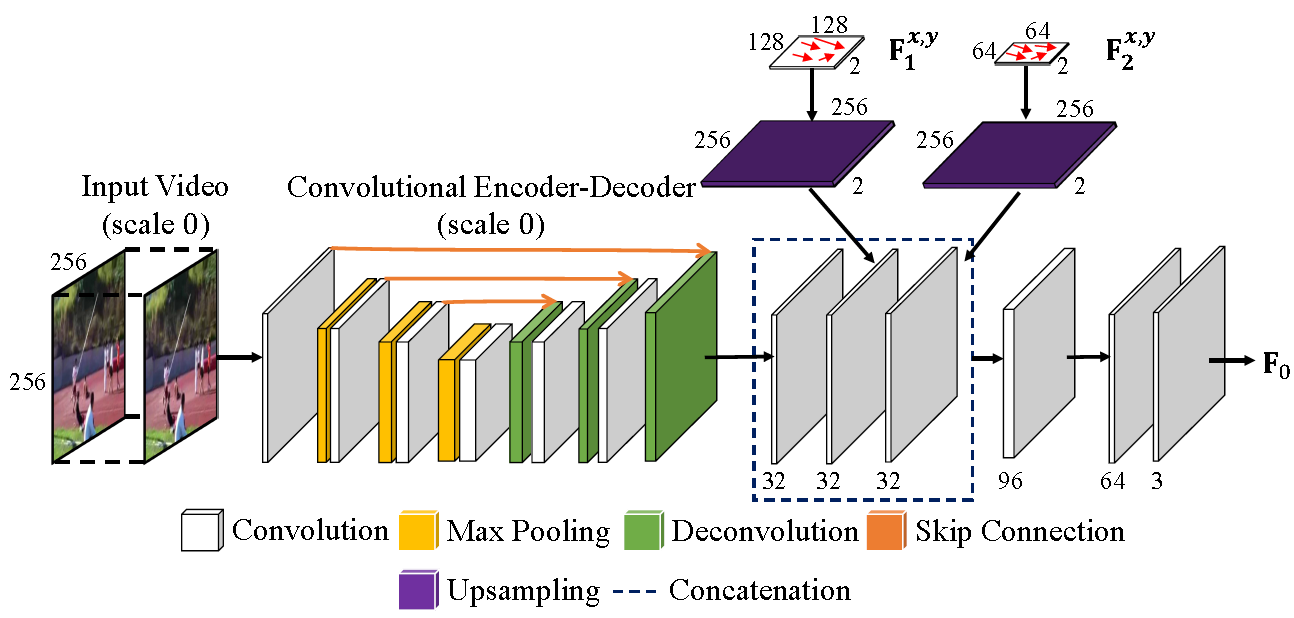
\hat{Y}_0=\mathcal{T}(X,F_0)=\mathcal{T}(X,\mathcal{H}(X;\Theta,F_N,\ldots,F_1))
Y^0=T(X,F0)=T(X,H(X;Θ,FN,…,F1))\hat{Y}_0=\mathcal{T}(X,F_0)=\mathcal{T}(X,\mathcal{H}(X;\Theta,F_N,\ldots,F_1))

Refinement

Multi-scale Flow Fusion

Extension

Multi-step Prediction

Predict D frames given current L frames

\hat{Y} \in \mathbb{R}^{H \times W}\Rightarrow \hat{Y} \in \mathbb{R}^{H \times W \times D}
Y^∈RH×W⇒Y^∈RH×W×D\hat{Y} \in \mathbb{R}^{H \times W}\Rightarrow \hat{Y} \in \mathbb{R}^{H \times W \times D}
\hat{Y}(x,y)\Rightarrow \hat{Y}(x,y,t)
Y^(x,y)⇒Y^(x,y,t)\hat{Y}(x,y)\Rightarrow \hat{Y}(x,y,t)

Smaller learning rate: 0.00005

Experiment

Compete with the State-of-the-art

Training set: UCF-101 Train, 240k triplets

Test set: UCF-101 Test, THUMOS-15

Competing methods (state-of-the-art)

  • EpicFlow + algorithm from Middlebury interpolation benchmark
  • BeyondMSE(with little tweaks)

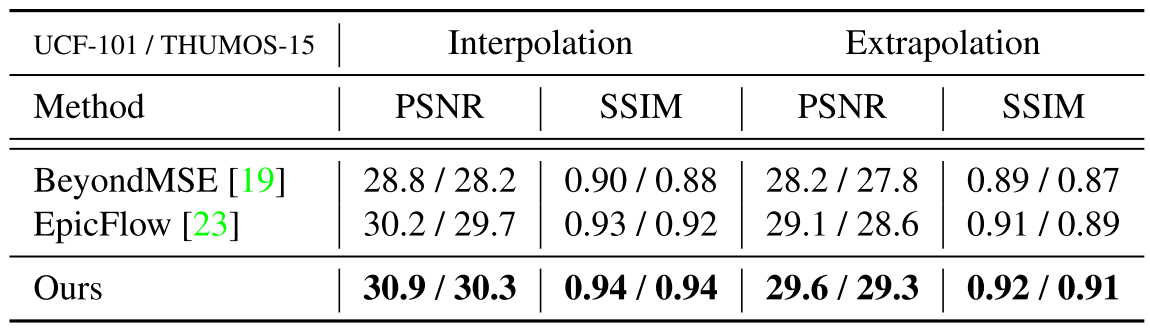
Experiment

Compete with the State-of-the-art

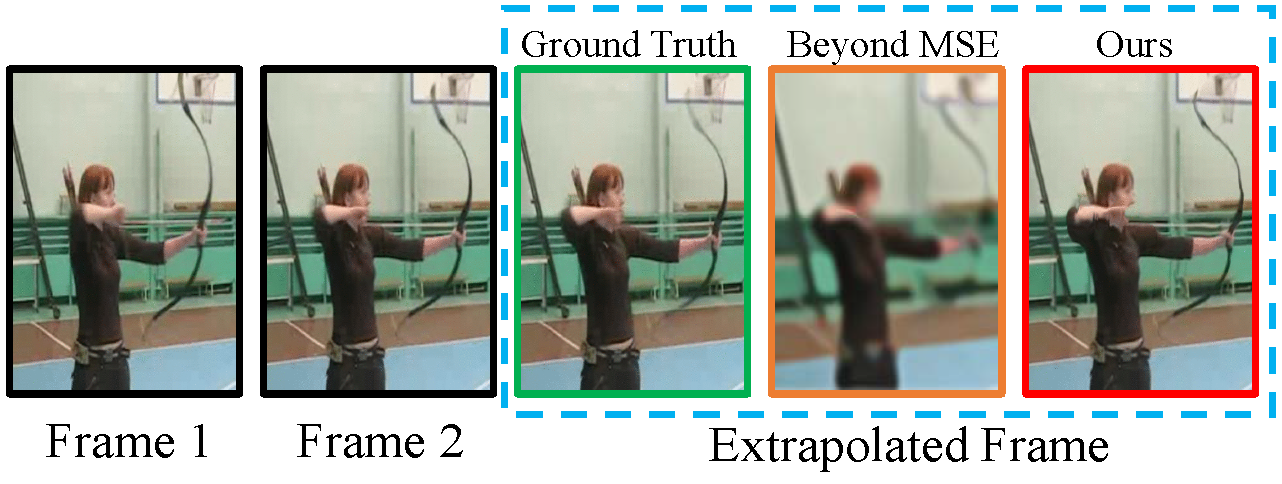
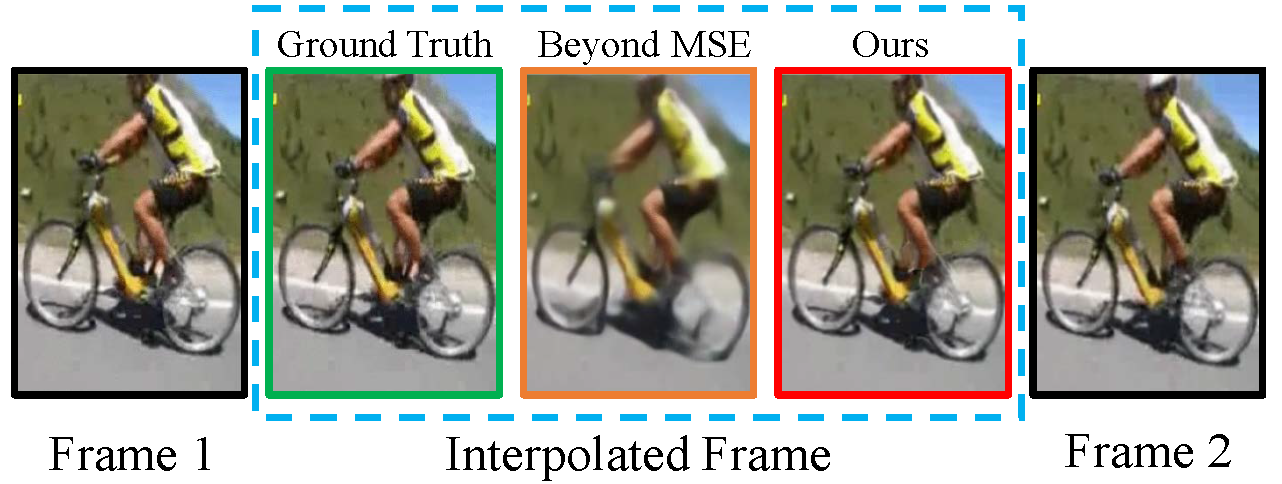
Experiment

Compete with the State-of-the-art

Interpolation

Extrapolation

Multi-step comparisons

Experiment

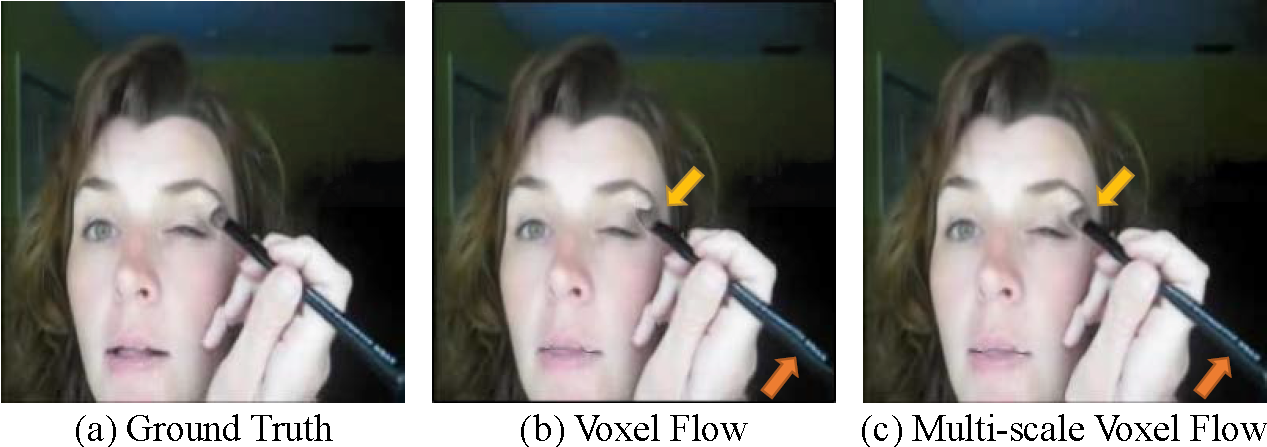
Effectiveness of Multi-scale Voxel Flow

Appearance

Motion

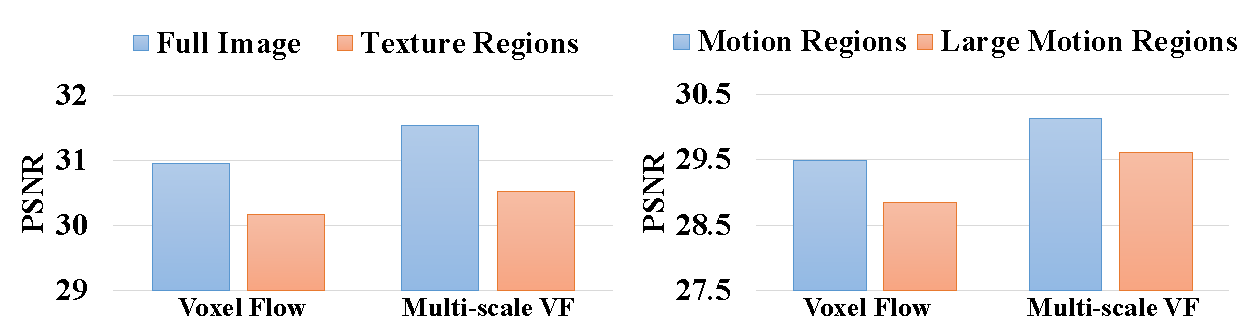
UCF-101 test set

Experiment

Generalization to View Synthesis

Evaluate KTTI odometry dataset

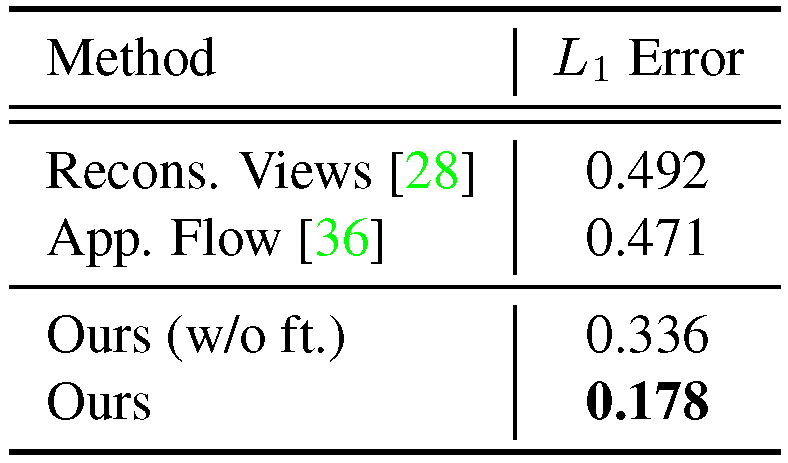
Experiment

Generalization to View Synthesis

Experiment

Frame Synthesis as Self-Supervision

Video frame synthesis can serve as a self-supervision task for representation learning(                  )

Flow estimation

(endpoint error)

Action recognition

\mathcal{H}\left( X;\Theta \right)
H(X;Θ)\mathcal{H}\left( X;\Theta \right)

Experiment

Application

Produce slow-motion effects on HD videos(1080x720, 30fps)

  • Visual Comparison
  • User Study

EpicFlow serve as a strong baseline

Experiment

Application-Visual Comparison

EpicFlow

Ground Truth

DVF

Experiment

Application-Visual Comparison

EpicFlow

Ground Truth

DVF

Experiment

Application-User Study

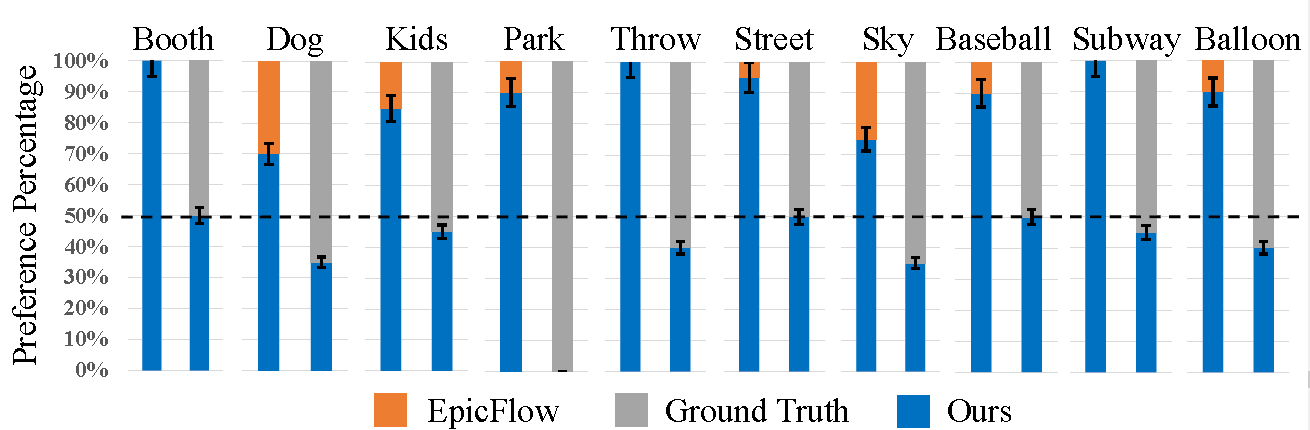
20 subjects were enrolled

For the null hypothesis:

  • "EpicFlow is better than our method"
    p-value < 0.00001
  • "DVF is better than ground truth"
    p-value < 0.838193

Experiment

Demo Video

Summary

  • End-to-end deep network
  • Copy pixels from existing video frames, rather than hallucinate them from scratch
  • Improves upon both optical flow and recent CNN techniques

Future Work

  • Combine flow layers with pure synthesis layers
    ⇒ predict pixels that cannot be copied from other video frames
  • Use the desired temporal step as an input
  • Compress the network, and run on mobile devices

Video Frame Synthesis using Deep Voxel Flow

By Maeglin Liao

Made with Slides.com

Video Frame Synthesis using Deep Voxel Flow

  • 445

More from Maeglin Liao