Drzewa decyzyjne

Michał Bieroński, 218324

Mateusz Burniak, 218321

Agenda

  • Definicja
    • Terminologia
  • Porównanie do modeli liniowych
  • Przykład niealgorytmiczny
  • Metody
    • Przyrost informacji
    • Chi-Kwadrat
    • Wskaźnik Giniego
    • Redukcja wariancji
  • Unikanie przeuczenia
  • Inne zastosowania
  • Random Forest
  • Podsumowanie

Drzewo decyzyjne

  • Algorytm uczenia nadzorowanego
  • Zmienne ciągłe i dyskretne

Polega na sekwencyjnym dzieleniu zbiorów na dwa rozłączne i dopełniające się podzbiory tak, by były możliwie jednorodne.

Drzewo (graf)

  • acykliczny
  • spójny

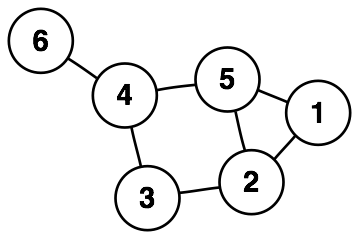
Terminologia

Terminologia

  • Korzeń - reprezentuje całą populację lub próbkę, która będzie podzielona na 2 jednorodne zbiory
  • Rozdzielenie - proces dzielenia węzła na pod-węzły
  • Węzeł decyzyjny - węzeł, który się dzieli na pod-węzły
  • Liść / węzeł końcowy - węzeł, który się nie dzieli
  • Przycinanie - proces usuwania pod-węzłów z węzła decyzyjnego
  • Gałąź / pod-drzewo - podgrupa całego drzewa
  • Węzeł, który jest dzielony na pod-węzły, jest rodzicem pod-węzłów, a pod-węzeł jest dzieckiem rodzica

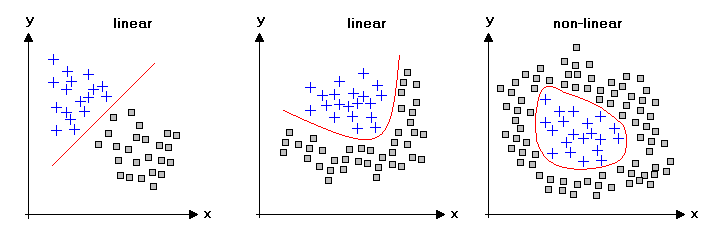
Drzewa vs modele liniowe

Drzewo skonstruowane bez heurystyki

Entropia

Który z trzech węzłów może zostać łatwo opisany?

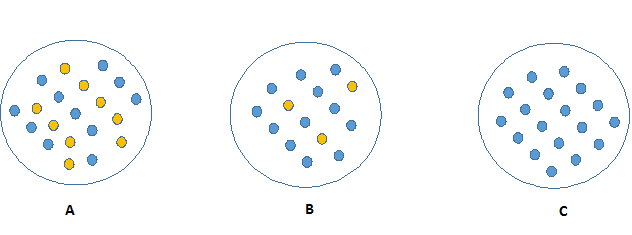
Konkluzja: im bardziej nieczysty węzeł - tym więcej potrzeba informacji by go opisać.

Entropia

  • Próbka homogeniczna - entropia 0
  • Próbka 50-50 - entropia 1

Entropia

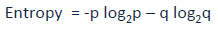
Gdzie p i q oznaczają odpowiednio prawdopodobieństwo sukcesu i porażki w danym węźle.

Można to wykorzystać w przypadku kategoryzacji - podział węzła.

Konstrukcja drzewa

  1. Drzewo zaczyna od pojedynczego węzła reprezentującego cały zbiór treningowy.

  2. Jeżeli wszystkie przykłady należą do jednej klasy decyzyjnej, to zbadany węzeł staje się liściem i jest on etykietowany tą decyzją.

  3. W przeciwnym przypadku algorytm wykorzystuje miarę entropii jako heurystyki do wyboru atrybutu, który najlepiej dzieli zbiór przykładów treningowych.

  4. Dla każdego wyniku testu tworzy się jedno odgałęzienie i przykłady treningowe są odpowiednio rozdzielone do nowych węzłów (poddrzew).

  5. Algorytm działa dalej w rekurencyjny sposób dla zbiorów przykładów przydzielonych do poddrzew.

  6. Algorytm kończy się, gdy kryterium stopu jest spełnione.

Konstrukcja drzewa

Kryterium stopu

  1. Wszystkie przykłady przydzielone do danego węzła należą do jednej klasy decyzyjnej
  2. Nie istnieje atrybut, który może dalej podzielić zbiór przykładów. W tym przypadku, liść jest etykietowany nie jedną wartością decyzji, lecz wektorem wartości zwanym rozkładem decyzji
  3. Wszystkie liście mają założoną z góry przewagę jednej klasy decyzyjnej (np. w żadnym nie ma mniej, niż 1% obiektów z innych klas, niż dominująca).

Podział węzła

Kategoria 1 0
Płeć K M
Wzrost Wysoki Niski
Klasa IX X
Gra Tak Nie

Kompletne drzewo

Text

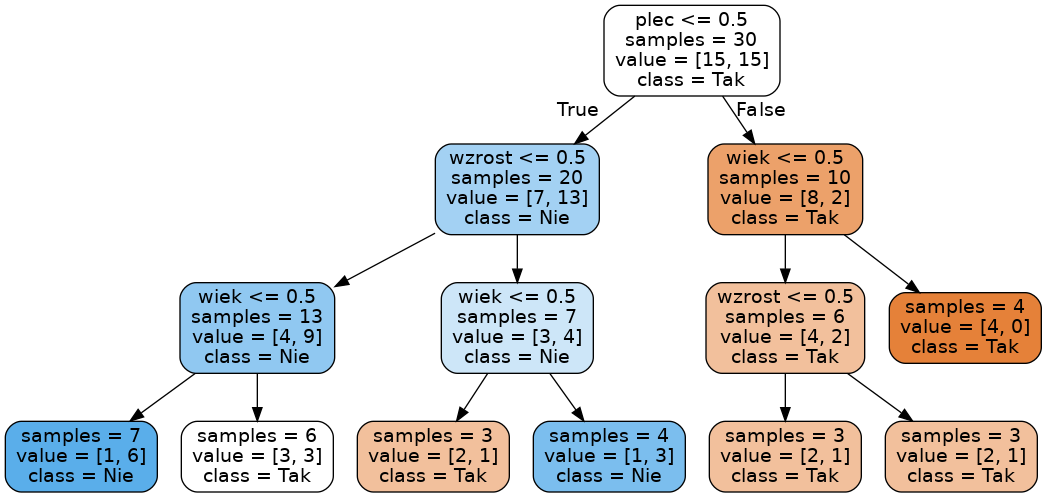
Kod

Text

import pandas as pd
from sklearn import tree
from sklearn.externals.six import StringIO
import pydotplus

df = pd.read_csv("data.csv", header=0)
original_headers = list(df.columns.values)
df = df._get_numeric_data()

numpy_array = df.as_matrix()
X = numpy_array[:, :3]
Y = numpy_array[:, -1]

clf = tree.DecisionTreeClassifier(criterion="entropy")
clf = clf.fit(X, Y)

dot_data = StringIO()
tree.export_graphviz(clf,
                     out_file=dot_data,
                     feature_names=original_headers[:3],
                     class_names=['Tak', 'Nie'],
                     filled=True, rounded=True,
                     impurity=False)

graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_pdf("cricket.pdf")
graph.write_png("cricket.png")

Klasyfikacja irysów

Chi-kwadrat

Metoda pozwalająca na znalezienie różnic statystycznych pomiędzy podwęzłami, a węzłem rodzicem.

  • działa dla kategorii docelowej "Sukces" lub "Porażka"
  • może dokonać dwóch lub więcej podziałów
  • im wyższa wartość tym większa rozbieżność względem węzła rodzica
  •  
  • tworzy drzewo zwane (CHAID Chi-square Automatic Interaction Detector)
ChiSquare = (((Actual-Expected)^2/Expected))^2
ChiSquare=(((Actual−Expected)2/Expected))2ChiSquare = (((Actual-Expected)^2/Expected))^2

Przykład

  • Spodziewana wartość obliczana jest na podstawie prawdopodobieństwa węzła rodzica, które tutaj wynosi 50%.
  • Pojedynczy wynik obliczany jest na podstawie wzoru:                
  • Wynik finalny dla danej kategorii jest sumą wszystkich podwyników
ChiSquare = (((Actual-Expected)^2/Expected))^2
ChiSquare=(((Actual−Expected)2/Expected))2ChiSquare = (((Actual-Expected)^2/Expected))^2

Współczynnik Giniego

  • Działa z etykietami dyskretnymi:
    "sukces" i "porażka"
  • Dzieli binarnie
  • Im wyższy wskaźnik,
    tym wyższa jednorodność
  • CART używa metody Giniego do podziału

Corrado Gini, XX w.,
włoski statystyk
i demograf

Jeśli populacja jest czysta, to losowy wybór dwóch danych, które należą do tej samej klasy występuje z prawdopodobieństwem równym 1.

Algrorytm Gini Index

  1. Oblicz współczynnik dla pod-węzłów używając funkcji f
  2. Oblicz współczynnik ważony dla każdego węzła
f = p^2 + q^2
f=p2+q2f = p^2 + q^2

\( p \) - prawdopodobieństwo sukcesu

\( q \) - prawdopodobieństwo porażki

Gini dla kobiet: \( 0.2^2 + 0.8^2 = 0.68 \)

Gini dla mężczyzn: \( 0.65^2 + 0.35^2 = 0.55 \)

Średnia ważona dla płci: \( \frac{10}{30} \times 0.68 + \frac{20}{30} \times 0.55 = 0.59 \)

Gini dla młodszych: \( 0.43^2 + 0.57^2 = 0.51 \)

Gini dla starszych: \( 0.56^2 + 0.44^2 = 0.51 \)

Średnia ważona dla wieku: \( \frac{14}{30} \times 0.51 + \frac{16}{30} \times 0.51 = 0.51 \)

Który podział jest lepszy?

  • Gini Index względem płci to 0,59
  • Gini Index względem wieku to 0,51

Redukcja wariancji

  • Wybór najlepszego podziału
  • Działa na danych ciągłych
  • Im niższa wariancja, tym lepszy podział

Kroki algorytmu

Podobnie jak poprzednio

  1. Oblicz wariancję dla każdego pod-węzła
  2. Oblicz wariancję ważoną dla każdego węzła
Var = \frac {\sum {(X - \bar X) ^ 2}}{n}
Var=∑(X−X¯)2nVar = \frac {\sum {(X - \bar X) ^ 2}}{n}

\( \bar X \) - to średnia

\( X \) - wartość aktualna

\( n \) - liczba wartości

Dla kobiet:

\( \bar X = \frac {2 \times 1 + 8 \times 0} {10} = 0.2 \)

\( Var = \frac {2 \times (1 -0.2)^2 + 8 \times (0-0.2)^2} {10} \)

\( Var = 0.16 \)

 

Dla mężczyzn:

\( \bar X = \frac {13 \times 1 + 7 \times 0} {20} = 0.65 \)

\( Var = \frac {13 \times (1 -0.65)^2 + 7 \times (0-0.65)^2} {20} \)

\( Var = 0.23\)

 

Wariancja ważona dla płci: \( \frac{10}{30} \times 0.16 + \frac{20}{30} \times 0.23 = 0.21 \)

Dla młodszych:

\( \bar X = \frac {6 \times 1 + 8 \times 0} {14} = 0.43 \)

\( Var = \frac {6 \times (1 -0.43)^2 + 8 \times (0-0.43)^2} {14} = 0.24 \)

Dla starszych:

\( \bar X = \frac {9 \times 1 + 7 \times 0} {16} = 0.56 \)

\( Var = \frac {9 \times (1 -0.56)^2 + 7 \times (0-0.56)^2} {16} = 0.25 \)

Wariancja ważona dla wieku: \( \frac{14}{30} \times 0.24 + \frac{16}{30} \times 0.25 = 0.25 \)

Który podział jest lepszy?

  • Wariancja względem płci to 0,21
  • Wariancja względem wieku to 0,25

Unikanie przeuczenia

Ograniczenia
na rozmiarze

Przycinanie drzewa

  • Od góry do dołu
  • Od liści do korzenia
  • Trzy główne algorytmy:
    • Reduced error pruning
    • Cost complexity pruning
    • Statistic-based pruning

Inne zastosowania

Random forest

  • Łączenie drzew w multiklasyfikator
  • Korzysta z baggingu i boostingu
  • Zwiększa dokładność predykcji

Podsumowanie

Zalety

  • Łatwe w zrozumieniu i interpretacji
  • Użyteczne w eksploracji danych
  • Dane wymagają mniej przygotowania
  • Typ danych nie jest ograniczeniem
  • Metoda nie parametryczna
  • Lepiej sprawują się w przypadku przestrzeni liniowo nie separowalnej

Podsumowanie

Wady

  • Narażone na przeuczenie
  • Nie nadają się dla zmiennych ciągłych

Bibliografia

Michał Bieroński, 218324

Mateusz Burniak, 218321

drzewa-decyzyjne

By Mateusz Burniak

Made with Slides.com

drzewa-decyzyjne

  • 634

More from Mateusz Burniak