MACs

Mateo Sanabria Ardila
Introducción a la criptografía
Un MAC (message authentication code) es una checksum criptográfica sobre los datos que utiliza una clave de sesión para detectar modificaciones tanto accidentales como intencionales de los datos
Autenticidad/Firma digitales usando criptografía simétrica
Firma Digital: MAC


\tiny (x,m)


secure channel
\tiny m = MAC_{k}(x)
\tiny m' = MAC_{k}(x)
\tiny m' = m \ (?)
Propiedades de MAC
-
No límite de tamaño de entrada
-
Tamaño fijo de salida
-
Bob tiene seguridad que Alice le envió el mensaje (Message Authentication)
- Alteraciones en la transmisión deben ser detectadas (Integrity)
- No repudio no se mantiene
Funciones Hash & MACs
m = MAC_{k}(x) = H(\alpha(k,x))
Como operar k,x para poder usar la función de hash H
-
m = H(k || x ) -> 'secret prefix'
-
m = H(x || k ) -> 'secret suffix'
secret prefix
m = H(k || x ) -> 'secret prefix'
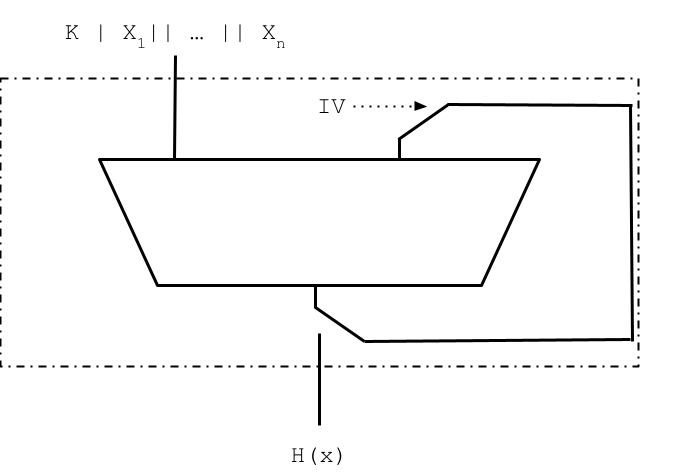
Firma Digital: MAC SECRET PREFIX


\tiny (x,m)
\tiny m = H(k || x_1 || \cdots || x_n)

\tiny x' = x_1 || ... || x_n || \textcolor{red}{x_{n+1}}
\tiny m' = H(x_{n+1}) \ \ \textbf{IV} = m
\tiny (x',m')
\tiny m'' = H(k || x_1 || \cdots || x_n || x_{n+1} )
\tiny m' = m '' \ (?)
Noten que el pinzas no tiene información del la clave simétrica K
Firma Digital: MAC SECRET PREFIX
El ataque no funciona si se hace padding con la longitud de la información que se esta usando!

secret suffix
m = H(x || k ) -> 'secret suffix'
Suponga que el pinzas logra encontrar una colisión
\small x \not = x' \ : \ H(x) = H(x')

Si el pinzas tiene que encontrar una colisión, vale la pena este ataque? es mejor que hacer fuerza bruta?


SHA-1
Fuerza bruta
2^{160}
Paradoja del cumpleaños
\sqrt{2^{160}} \approx 2^{80}
AES-128b
Fuerza bruta
2^{128}
hmac: overview
HMAC_k (x) = H(k || H(k || x ))
hmac
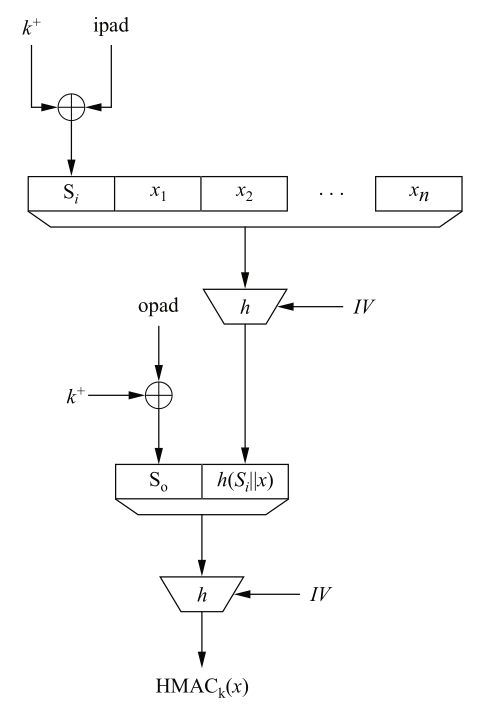
H((k^+ \oplus opad ) || H((K^+ \oplus ipad) || x ))
HMAC_k (x) =
k^+ = 0 \cdots 0 || k
ipad = 0011 \ 0110, \cdots, 0011 \ 0110
opad = 0101 \ 1100, \cdots, 0101 \ 1100

MACs
By Mateo Sanabria Ardila
MACs
MACs
- 149



