Introdução à Estatística e Estatística Descritiva

Prof. Dr. Pedro Costa Ferreira

Pra que serve a Estatística?

  • Porque nos permite entender e lidar com a idéia de variabilidade;
  • Um exemplo típico é:

    Produção de parafusos. Uma fábrica produz parafusos, que devem ter diâmetros dentro de certas especificações. Ao medirmos os diâmetros de 100 parafusos produzidos ao acaso existirão variações individuais;

  • Estas variações são importantes? Até que ponto as variações observadas são aceitáveis?

Estatística

Em geral um número em Estatística não é apenas um número! A ele associamos uma medida de incerteza ou variabilidade.

População e Amostra

  • População: coleção de todos os elementos cujas características desejamos conhecer. Os elementos (ou "indivíduos") na população não são necessariamente pessoas!
  • Amostra: subconjunto da população cujas características serão medidas. A amostra será usada para descobrir características da população.

teste

Exemplos

População: eleitores na cidade do Rio de Janeiro.
Amostra: 650 eleitores escolhidos aleatoriamente (ao acaso).
Característica de interesse: percentual de eleitores que
planejam votar num candidato X nas próximas eleições.

População: automóveis produzidos no Brasil entre 1997 e 2002.
Amostra: 10000 carros escolhidos aleatoriamente dentre os sujeitos a recall das montadoras.
Característica de interesse: verificar se o proprietário do carro respondeu ao chamado de recall da fábrica.

1

2

Exemplos

População: todos os domicílios com TV na cidade do Rio de Janeiro.

Amostra: 1000 domicílios com TV escolhidos ao acaso.

Característica de interesse:  percentual de audiência de cada emissora de TV num certo dia da semana no horário de 18 às 22 horas.

Em resumo:  A partir de uma amostra coletamos informações  que nos permitem aprender alguma coisa interessante sobre a população.

3

Por que fazer isso?

  • É economicamente eficiente! Os custos são infinitamente mais baixos que os de amostrar a população inteira (“censo”).

  • Pode-se provar que, para populações muito grandes, uma amostra de cerca de 600 ou 1000 "indivíduos" fornece resultados bastante confiáveis sobre as características da população.

E agora?

  • Você coletou uma amostra e, dentro desta amostra você coletou dados numéricos (por exemplo, o consumo médio mensal em kWh dos domicílios numa certa área da cidade). O que fazer com isso?

Você pode simplesmente descrever estes dados numéricos através de gráficos e tabelas. Isto é chamado de estatística descritiva. A maioria das pesquisas de mercado faz só isso, que é sem dúvida, muito importante. 

Existem duas possibilidades:

1

E agora?

Você pode tentar tirar conclusões sobre as características da população a partir dos dados observados na amostra. 

Isso se chama estatística inferencial (ou simplesmente estatística!). Para que a gente consiga fazer isso, é necessário ter uma noção bastante abrangente de Probabilidades.

2

E agora?

  • Na verdade, a estatística descritiva surgiu muito antes da estatística inferencial.

  • Esta última depende da especificação de modelos matemáticos baseados numa noção fundamental, que é a de "probabilidade".

Estatística Descritiva

Estatística Descritiva

  • Gráficos (A picture is worth one thousand words)
  • Histograma
  • Diagramas de Pareto
  • Gráficos de dispersão, gráficos da variável ao longo do tempo, gráficos de barras, etc...
  • Medidas Númericas
  • Média amostral
  • Mediana amostral
  • Desvio padrão amostral
  • Variância amostral
  • Assimetria e Curtose amostrais
  • Percentis
  • Covariância e Correlação amostrais

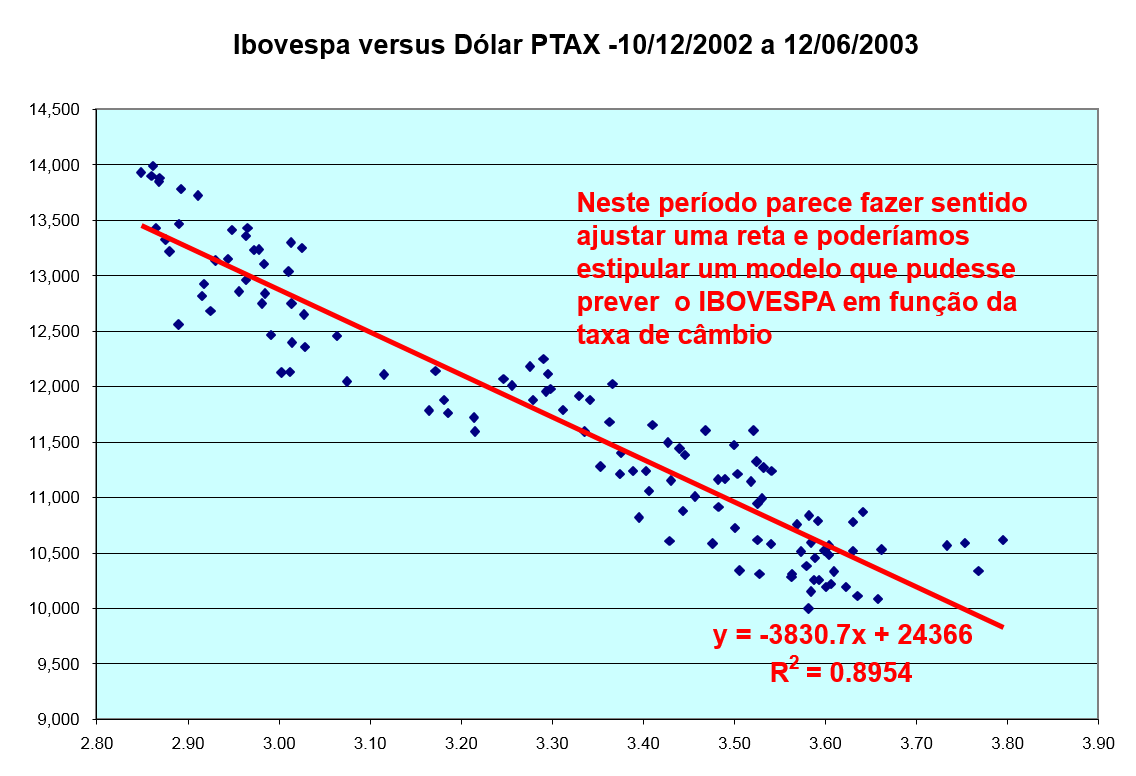
Gráfico de Dispersão
(uma variável versus outra)

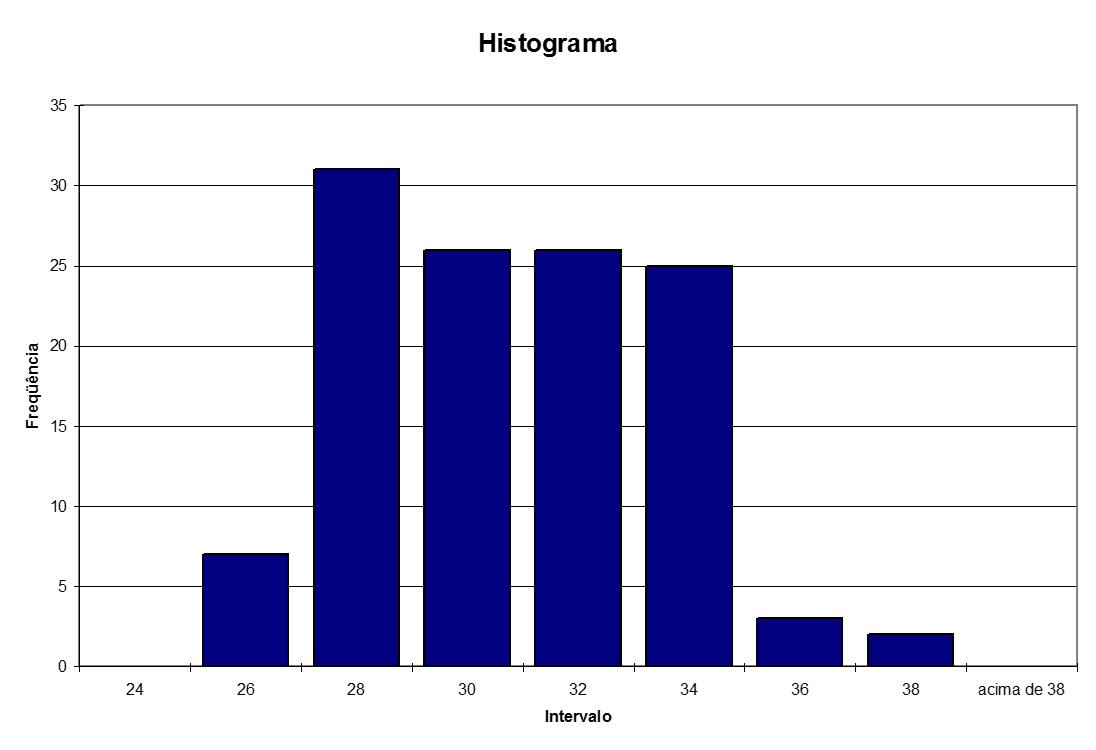
Histograma

Note que este histograma usa intervalos diferentes dos especificados na tabela de freqüência mostrada anteriormente

Histograma

Histograma – Retorno diário do preço do petróleo WTI – 01/1991 a 08/2006

Medidas Númericas

  • A  partir de agora  suponha que os  dados  observados  na  amostra  são 
x_1, x_2, x_3, ..., x_n;
x1,x2,x3,...,xn;x_1, x_2, x_3, ..., x_n;
  •    é o tamanho da amostra;
n
nn
  • A partir dos x's vamos encontrar números que resumem as características da amostra. Vamos estar interessados em dois tipos principais de medidas numéricas: as que caracterizam a localização do centro da amostra e as que caracterizam a dispersão dos dados.

Medidas Númericas

  • Medidas de Localização ou de tendência central
  • Medidas de Dispersão
  • dizem onde está o "meio" dos seus dados;

  • exemplo: média e mediana amostrais.

  • dizem o quanto os seus dados estão “espalhados”;

  • exemplo: desvio padrão e variância amostrais, amplitude amostral.

Medidas de Tendência Central

  • Média Amostral
\bar{X} = \frac{1}{2}\sum_{i=1}^{n} X_n
X¯=12∑i=1nXn\bar{X} = \frac{1}{2}\sum_{i=1}^{n} X_n
  • Considere agora a amostra                        e suponha que você a ordene, de tal forma que         seja o menor elemento da amostra,         seja o segundo menor elemento, ....,      seja o maior elemento da amostra. Os valores
                                  são chamados de estatísticas de ordem da amostra. Outras medidas de tendência central e de dispersão serão definidas a partir das estatísticas de ordem.
x_1, x_2, ..., x_n
x1,x2,...,xnx_1, x_2, ..., x_n
x_{(1)}
x(1)x_{(1)}
x_{(2)}
x(2)x_{(2)}
x_{(n)}
x(n)x_{(n)}
x_{(1)}, x_{(2)}, ..., x_{(n)}
x(1),x(2),...,x(n)x_{(1)}, x_{(2)}, ..., x_{(n)}

Medidas de Tendência Central

  • Mediana
    ​É definida a partir das estatísticas de ordem
m = \frac{ X_{(n/2) + X_{(n/2 + 1)}}}{2}
m=X(n/2)+X(n/2+1)2m = \frac{ X_{(n/2) + X_{(n/2 + 1)}}}{2}
m = X_{(n/2 + 1)}
m=X(n/2+1)m = X_{(n/2 + 1)}

Se n é par

Se n é impar

  • Por exemplo, se existem 10 observações na amostra, a mediana equivale à média entre          e          . Se a amostra contém 11 elementos, a mediana é         . A mediana amostral é menos influenciada que a média por observações aberrantes (“outliers”).
x_{(5)}
x(5)x_{(5)}
x_{(6)}
x(6)x_{(6)}
x_{(5)}
x(5)x_{(5)}

Medidas de Tendência Central

  • Por exemplo, se os seus dados são 1,2,3,4,5, a média amostral é: (1+2+3+4+5)/5 = 3 e a mediana amostral tem o mesmo valor.

  • Se agora os dados são: 1,2,3,4,45, a média amostral é: (1+2+3+4+45)/5 = 11, mas a mediana amostral continua sendo 3.

  • Logo, a média amostral foi profundamente influenciada por um único valor, e o mesmo não aconteceu com a mediana amostral.

Medidas de Dispersão

  • As medidas de tendência central não são as únicas medidas necessárias para caracterizar uma amostra (ou população);

  • Precisamos também saber o quanto as observações na amostra estão "espalhadas";

  • Por exemplo, no gráfico a seguir as populações têm a mesma média, mas certamente a segunda distribuição tem maior dispersão.

Medidas de Dispersão

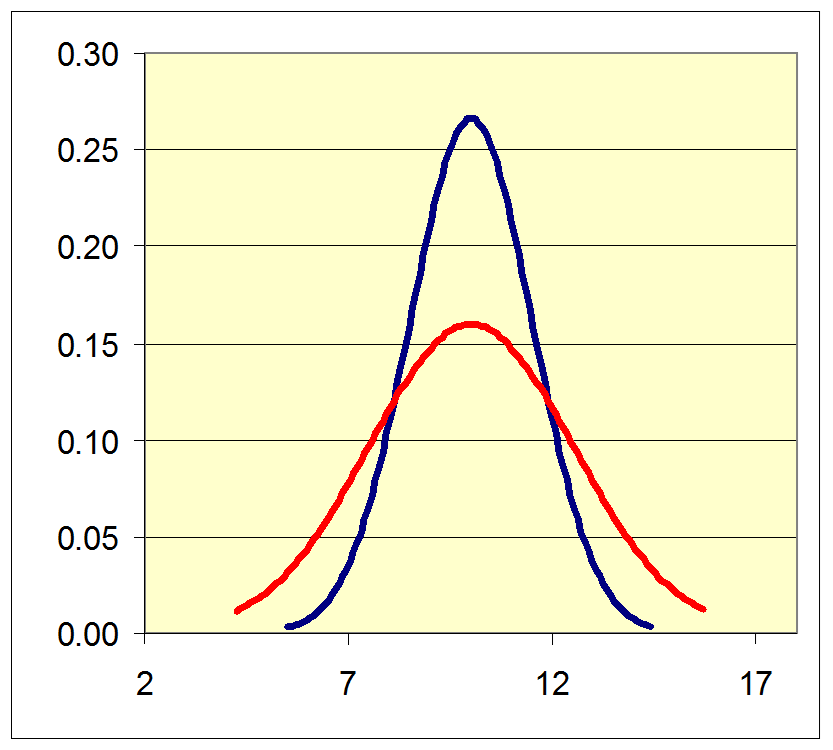
Tem maior dispersão:
é mais “espalhada”

Medidas de Dispersão

  • Variância Amostral
    É a medida mais comum de dispersão . A variância amostral, denotada por      é definida como:
s^2
s2s^2
s^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left ( X_i - \bar{X} \right )
s2=1n−1∑i=1n(Xi−X¯)s^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left ( X_i - \bar{X} \right )
  • Note que, por definição, a variância amostral é sempre não negativa!
  • A unidade de medida  da variância é o quadrado da unidade de medida das observações, o que dificulta a sua interpretação.

Medidas de Dispersão

  • Desvio Padrão Amostral
    O desvio padrão amostral, denotado por s, é definido como a raiz quadrada positiva da variância amostral. Pelos comentários anteriores, notamos que s é expresso nas mesmas unidades de medida que as observações na amostra.
s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} \left ( X_i - \bar{X} \right )}
s=s2=1n−1∑i=1n(Xi−Xˉ)s = \sqrt{s^2} = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} \left ( X_i - \bar{X} \right )}

Medidas de Dispersão

  • Coeficiente de variação amostral
    É uma medida adimensional, e serve principalmente para comparar duas amostras que foram coletadas em unidades de medida diferentes, por exemplo, uma em cm e outra em polegadas.
CV = \frac{s}{\bar{X}}
CV=sX¯CV = \frac{s}{\bar{X}}
  • Amplitude Amostral
A = X_{(n)} - X_{(1)}
A=X(n)−X(1)A = X_{(n)} - X_{(1)}

Percentis

  • O percentil x% é o ponto tal que, a probabilidade de estar abaixo dele é x%.
  • O percentil 50% é a mediana de um conjunto de dados, e qualquer percentil entre 0 e 100% pode ser encontrado através da função PERCENTIL do Excel.

Quartis

  • Primeiro Quartil: Q1 – é o percentil 25%, ou seja, 25% das observações estão abaixo de Q1
  • Segundo Quartil: Q2  - é a mediana

  • Terceiro Quartil: Q3 – é o percentil 75%

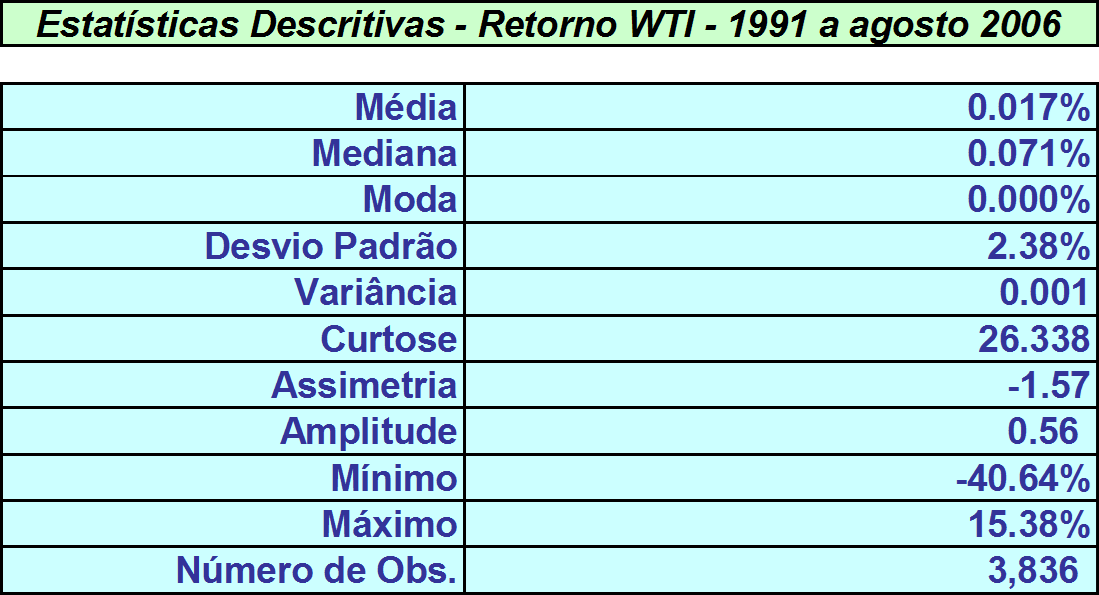
Estatísticas Descritivas – Retorno do Petróleo WTI – 01/1991 a 08/2006

Percentis – Retorno do Petróleo WTI
– 01/1991 a 08/2006

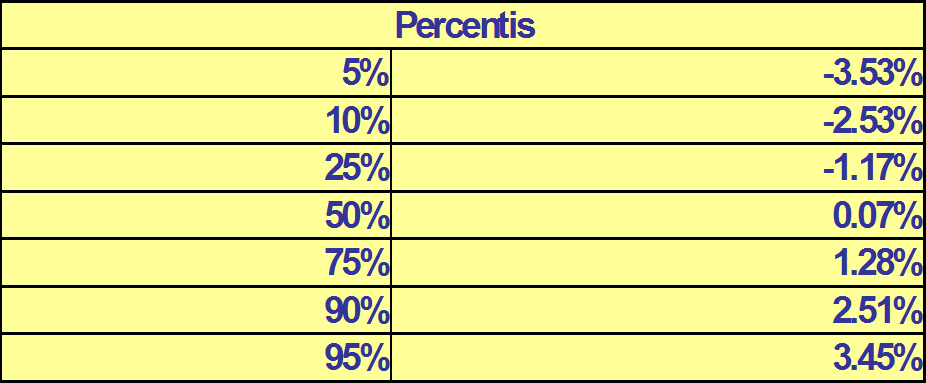
5% dos retornos abaixo de -3.53%

90% dos retornos abaixo de +2.51%

Boxplot

  • O boxplot dá uma idéia da posição, dispersão, assimetria, caudas e dados discrepantes;
  • A posição central é dada pela mediana e a dispersão por:

  • As posições relativas quartil 1, quartil 2 e quartil 3 dão uma noção da assimetria da distribuição;

  • Os comprimentos das caudas são dados pelas linhas que vão do retângulo aos valores remotos e pelos valores atípicos (outliers), que são, geralmente representados por asterísco.

d_p = Q_3 - Q_1
dp=Q3−Q1d_p = Q_3 - Q_1

Boxplot

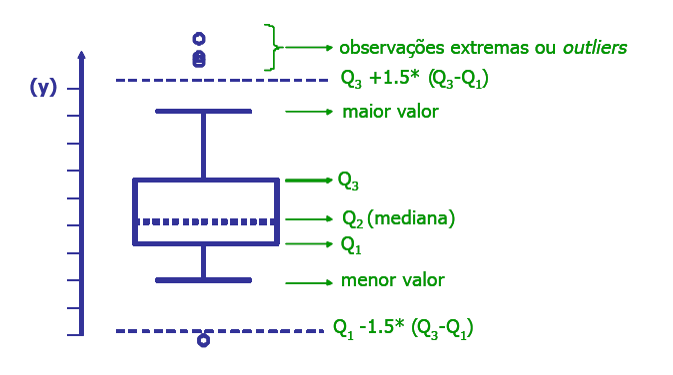
Assimetria

  • O coeficiente de assimetria amostral é definido como:

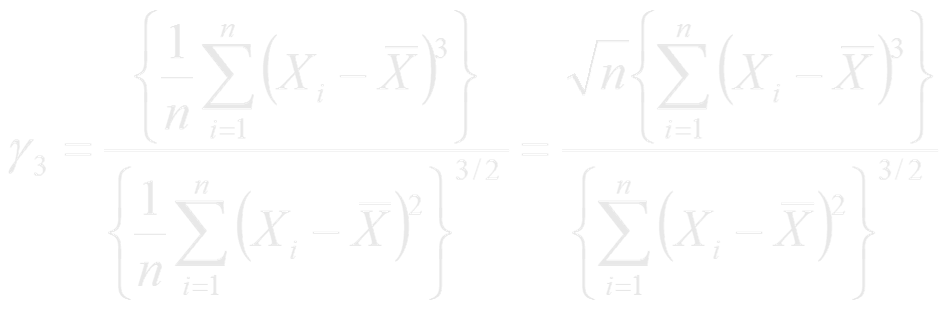
Se o coeficiente é zero, seus dados são simétricos em torno da média.
Se o coeficiente é positivo (assimetria positiva), existem valores “grandes” maiores que a média => existe uma cauda comprida para a direita.

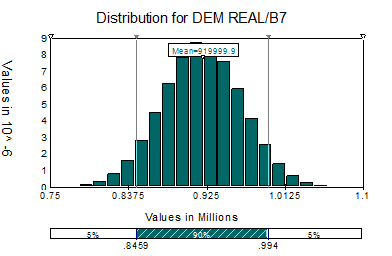
Assimetria

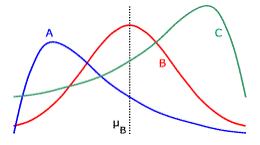
  • Em geral, se a assimetria é positiva, a média é maior que a mediana.
  • Na curva A acima a assimetria é positiva, a curva B é simétrica e a curva C tem assimetria negativa.
  • O oposto ocorre se a assimetria é negativa (em geral média menor que a mediana).

Assimetria

Dados com assimetria positiva

Dados simétricos

Curtose

  • É uma medida do “achatamento” de uma distribuição de probabilidade.

  • Como a distribuição Normal tem curtose igual a 3, usualmente define-se o “excesso de curtose”, ou seja, o quanto uma distribuição de probabilidade tem mais curtose que a Normal.

Curtose

  • Distribuições de retornos de ativos financeiros geralmente tem a “cara” de uma Normal, mas com excesso de curtose!

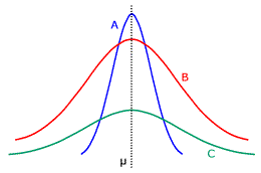
Ao lado, a curva B é a normal padrão
e a curva A tem excesso de curtose.

Introdução à Estatística e Estatística Descritiva

By Matheus Camelo

Made with Slides.com

Introdução à Estatística e Estatística Descritiva

  • 384

More from Matheus Camelo