Ранняя история и математические основы программирования:
Чёрч, Карри, Тьюринг
Кольцов Максим
Наивная теория множеств
Георг Кантор
- 1870-1900 — создание Кантором основных идей теории
- 1901— парадокс Рассела. Проблема теории Кантора — слишком "общее" построение множеств
\exists y \forall x (x \in y \Leftrightarrow P(x))
\forall x (x \in y \Leftrightarrow x \in\!\!\!\!\!/ \; x)
- 1908-1921 — аксиоматика ZF
- 1931 — теоремы Гёделя о неполноте
Математическая логика
- Классическая логика: исчисление высказываний
- Логика первого порядка: кванторы
- Интуиционистская логика: важность доказательства
- Математический конструктивизим
\frac{A \quad (A \to B)}{B}
Modus Ponens
Проблема останова
- Проблема Гильберта — есть ли алгоритм, доказывающий формулы?
- 1935-1936 — Алонзо Чёрч и Алан Тьюринг: нет
Алан Тьюринг
Алонзо Чёрч
Почему нет?
def g():
if halts(g):
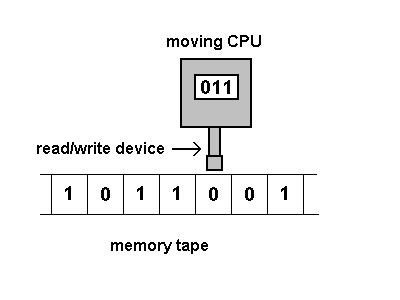
loop_forever()Машина Тьюринга
Бесконечная лента, головка и правила перехода
Лямбда-исчисление
-
Переменные: \( x \), \( y \)
-
Применение: \( f x \), \( f x y = (f x) y \)
-
Абстракция: \( \lambda x . f x \)
-
Бета-редукция:
$$ (\lambda x . f z) y = f y $$
-
Функции нескольких переменных? \( \lambda x . (\lambda y . f x y) \)
-
Рекурсия? \( Y=\lambda f\,.(\lambda x\,. f(x\ x))\;(\lambda x\,. f(x\ x)) \)
Проблема останова?
(\lambda x . x) (\lambda x . x)
Типизированное
λ-исчисление
- Каждая переменная имеет тип: \( e : \tau \)
- Если \( x : \sigma \), \(e : \tau \), то \( \lambda x . e : \sigma \to \tau \)
- Если \( e_1 : \sigma \to \tau \), \( e_2 : \sigma \), то \( e_1 e_2 : \tau \)
Haskell как реализация лямбда-исчисления
f :: Integer -> String
f = \x -> (show x) ++ "!"
b :: String
b = f 1
fact :: Integer -> Integer
fact 0 = 1
fact n = n * fact (n - 1)Изоморфизм
Карри-Говарда
Хаскел Карри
- Все высказывания — типы
- Есть терм — есть доказательство
\frac{A \quad (A \to B)}{B}
\qquad
\frac{a : A,\; f : A \to B}{f a : B}
\frac{A \vdash B}{A \to B}
\qquad
\frac{a : A \vdash b : B}{\lambda a . b : A \to B}
Автоматическое доказательство и проверка кода
- 1989 — первая версия доказывателя теорем
- 2004 — проверка теоремы о четырёх красках
- 2015 — баг в TimSort, найденный с помощью KeY
«Ранняя история и математические основы программирования: Чёрч, Карри, Тьюринг»
By Maxim Koltsov
