112 寒訓四小SLIDES 成發
雜談海龍公式
112 寒訓四小隊員 製
1
小學數學
2
國中初等幾何
3
高中數學
5
大學必修線性代數
4
海龍公式（終於出現了）
6
延延伸&references
1. 小學數學
如圖，底為 d，底上的高為 h，面積 A 則為則 $$ \frac{1}{2}dh $$
2. 國中初等幾何
內切圓
如圖，內切圓I半徑為r，令半周長$$ s = \frac{a+b+c}{2} $$
顯然面積A是 rs
三條頂點與對面切點的連線也會共點
BTW 那個叫熱爾崗點(Gergonne Point)
3. 高中數學
3.1 正弦函數+SAS
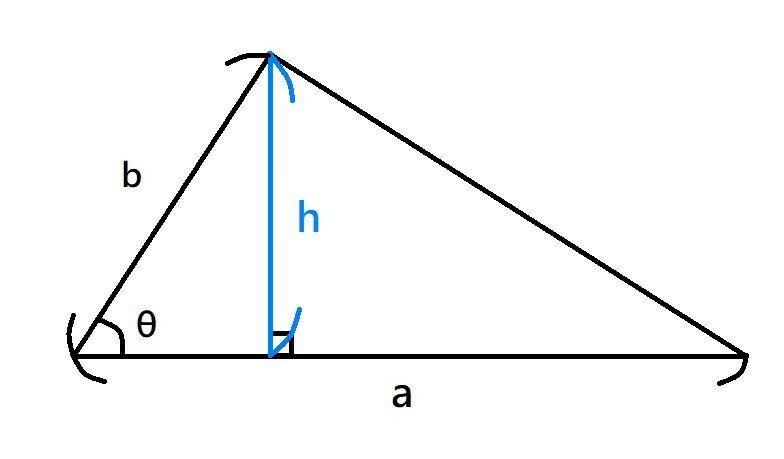
如圖，兩邊a,b夾\( \theta \) ，觀察得高h為\( b\sin \theta \)
所以面積A則為\( \frac{1}{2}ab\sin \theta \)
3. 高中數學
3.2 外接圓
如圖，外接圓O半徑為R，由正弦定理知$$\sin \angle \; C = \frac{c}{2R}$$
所以面積A(三角形面積)為$$\frac{abc}{4R}$$
4. 海龍公式（終於出現了）
4.1 小簡介
海龍公式，由古希臘亞歷山卓數學家海龍發現，證明
令三角形半周長為\( s = \frac{a+b+c}{2} \)，則其面積
$$A = \sqrt{s(s-a)(s-b)(s-c)}$$
事實上在12世紀中國南宋末年數學家秦九韶也發現了等價的公式，其著作《數書九章》(1247年)卷五第二題即三斜求積術。原文翻譯後即為$$ A = \sqrt{\frac{1}{4}[a^2 c^2 - (\frac{a^2+c^2-b^2}{2})^2]},where \quad a \geq b \geq c $$
4. 海龍公式（終於出現了）
4.2 極簡證明
1. 用3.1 正弦函數表示三角形面積
2. \( \sin^2 \theta \)用\( 1-\cos^2 \theta \)
3. \( \cos \theta \)用餘弦定理代換
4. 兩次平方差公式 ■
4.2.1 你（未來）在課本上看到的東西
4. 海龍公式（終於出現了）
4.2 極簡證明
因為
由(2)-(3) 並以平方差公式展開，再用(1)代換得d-e的表達式
由(1)+(4)消去e得d的表達式
\( \because A = \frac{1}{2}ch \)，並將h以(2)代入即得證
4.2.2 畢氏定理
\left\{\begin{array}{lll}
c &= d + e&(1)\\
a^2 &= h^2 + d^2&(2)\\
b^2 &= h^2 + e^2&(3)
\end{array} \right.
4. 海龍公式（終於出現了）
4.3 小小應用
開算幾得$$\frac{(s-a)+(s-b)+(s-c)}{3} \geq \sqrt[3]{(s-a)(s-b)(s-c)}$$
等號成立即\( s-a = s-b = s-c \Rightarrow a = b = c \)
又\( s = \frac{a+b+c}{2} = \frac{3a}{2} \)
代回整理知$$(\frac{s}{3})^3 = (\frac{a}{2})^3 = (s-a)(s-b)(s-c)$$
海龍一下知$$A = \sqrt{\frac{3a}{2} \times (\frac{a}{2})^3} = \frac{\sqrt{3}}{4}a^2$$
4.3.1 證明當三角形的周長固定時，正三角形的面積最大並用邊長表示面積
4. 海龍公式（終於出現了）
4.3 小小應用
在\( \triangle ABC \)中，若\( \overline{AB} \)的長度是7，且長度\( \frac{\overline{BC}}{\overline{CA}}=\frac{24}{25} \)，則\( \triangle ABC \)面積的最大值為________ 。
4.3.2 105建中科學班數學科填充第二題
設三邊為7,24r,25r
海龍一下知
$$ \triangle = \sqrt{\frac{49r+7}{2}\times\frac{49r-7}{2}\times\frac{r+7}{2}\times\frac{7-r}{2}}$$
$$ = \frac{1}{4}\sqrt{[(49r)^2-7^2](7^2-r^2)}$$
$$ = \frac{7}{4}\sqrt{[(7r)^2-1](7^2-r^2)}$$
$$ let\quad a=r^2 $$
$$ = \frac{7}{4}\sqrt{(49a-1)(49-a)} $$
當\( a = \frac{\frac{1}{49}+49}{2} \)(兩解之平均)，
$$\triangle_{max} = \frac{7}{4}\sqrt{(\frac{1+49^2}{2}-1)(\frac{49-\frac{1}{49}}{2})} = 300_{\quad\#}$$
4. 海龍公式（終於出現了）
4.3 小小應用
4.3.3 計算多邊形面積
n邊的多邊形分割成n-2個三角形
5. 大學必修線性代數
來不及了，自己去看講義！
6. 延延伸和references
6.1 延延伸
皮克定理/Pick 公式 詳見參考資料4
婆羅摩笈多公式 詳見參考資料 6
布雷特施奈德公式 詳見參考資料7
6. 延延伸和references
1. 數學之旅：三角形面積公式 (I)
2. 數學之旅：三角形面積公式 (II)
3. 數學之旅：三角形面積公式 (III)
4. 數學之旅：三角形面積公式 (IV)
5. 海龍公式
6. 婆羅摩笈多公式
7. 布雷特施奈德公式
8. 淺談 - 三角形面積公式
6.2 references
謝謝大家
謝謝大家~
112 寒訓四小SLIDES成發
By MH Yang
