Chapter 1:

Probabilistic inference

& Graph models

slabod@, 08.12.2017

Анонс: Определения

  1. Теория вероятностей
  2. Графы
  3. Обозначения

  4. BRMLtoolbox for MATLAB

Анонс: Probabilistic reasoning & inference

Анонс: Grap models

Анонс: Grap models

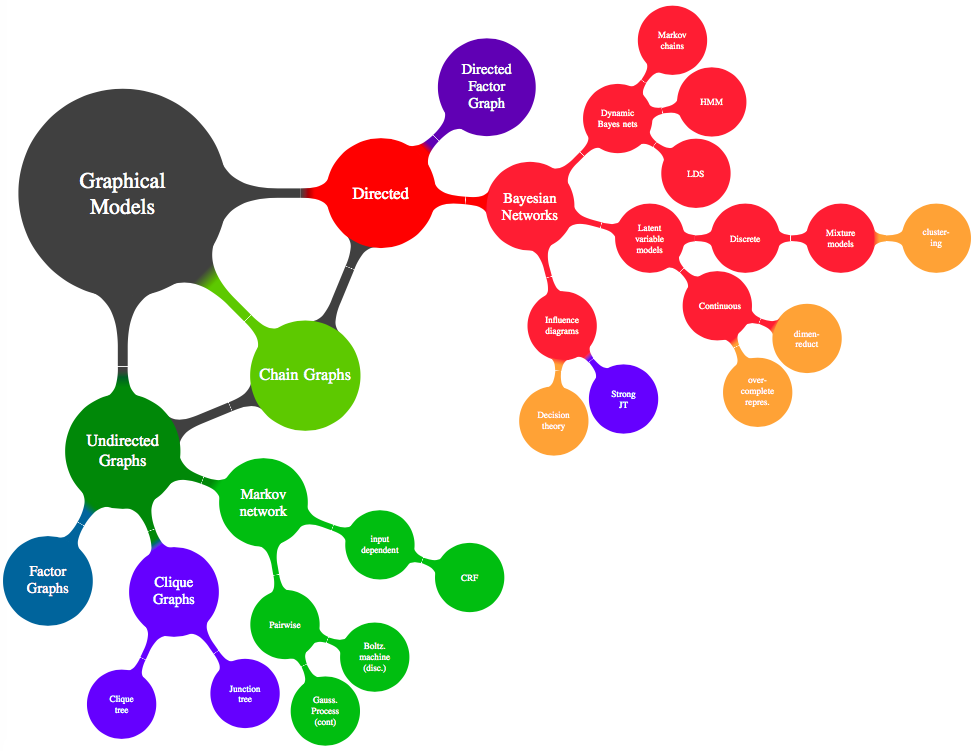
Обозначения 

  • Вероятностное пространство:
    \( ( \Omega, A, \mathbb{P} )\)
  • Переменные:
    \(x\)
  • События:
    \(A\)
  • Область значений
    \(x:\) \(dom(x)\)
  • Суммирование по значениям:
    \(\sum_x f(x) = \sum_{s \in dom(x)} f(s)\)

Обозначения: вероятности

  1. x — булева
    \(p(x = tr)\)
  2. x — дискретная с. в., \(dom(x)\) конечна
    \(p(x)\) = \(p(x = a), a \in dom(x)\)
  3. x - произвольная с. в.
    \(p(x)\) =     \(p(x \in A)\)
  4. \(p(x | y) \,=\, p(x = a \,|\, y = b)\)
  5. \(p(x | y) \,=\, p(x \in A \,|\, y \in B)\)
  6. \(p(A , B) \,=\, p(A \cap B )\)

Формула включений-исключений

p(x = a \vee y = b) \;=\; p(x = a) + p(y = b) - p(x = a \wedge y = b)
p(\bigcup\limits_i A_i) \;=\; \sum_i p(A_i) - \sum_{i, j} p(A_i \cap A_j) + \ldots + (-1)^{n-1} p(\bigcap_i A_i)

Marginalisation, совместное распределение

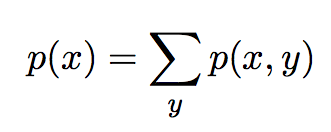
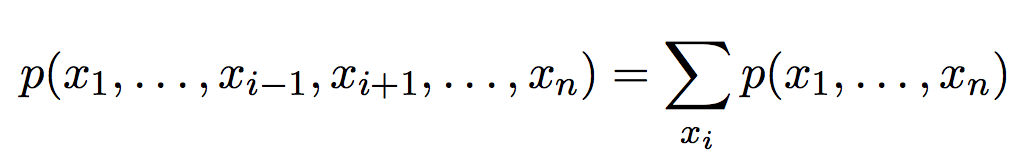
Плотность вероятности

f(t) \ge 0
\int\limits_{\mathbb{R}} f = 1
p(x \in A) = \int\limits_{A} f_x(t) dt

Условная вероятность, Bayes' rule

p(x | y) \longleftrightarrow p(y | x)

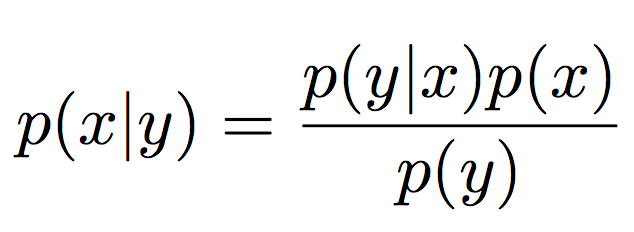
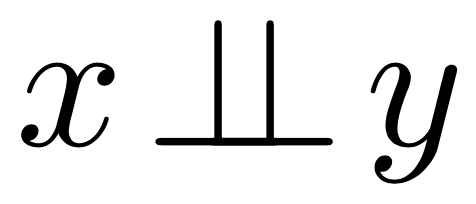
Независимость

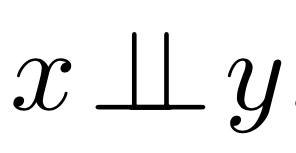
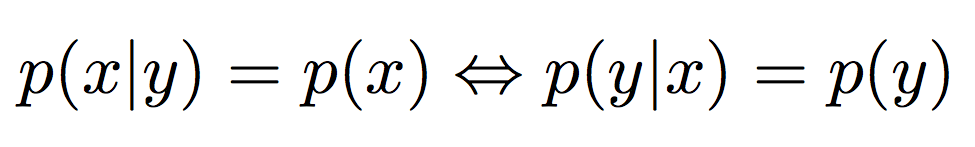
\Leftrightarrow
\Leftrightarrow
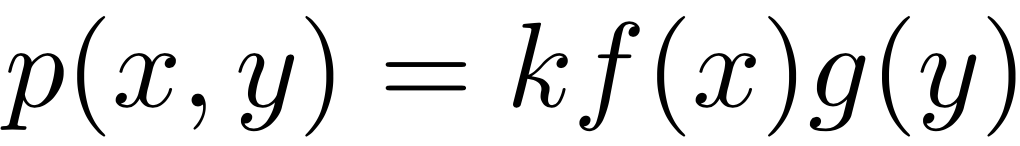
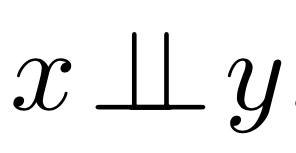
\Rightarrow

Условная независимость

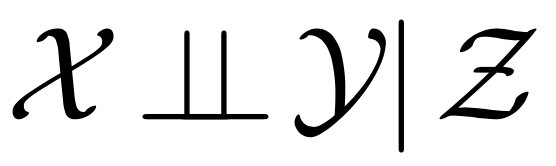
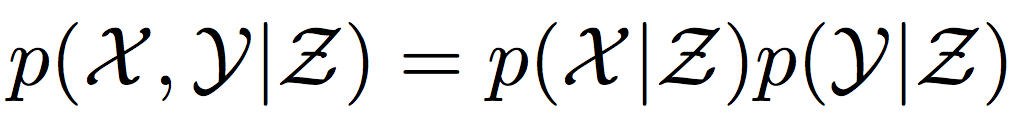
\Leftrightarrow
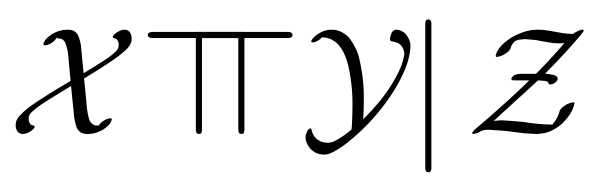
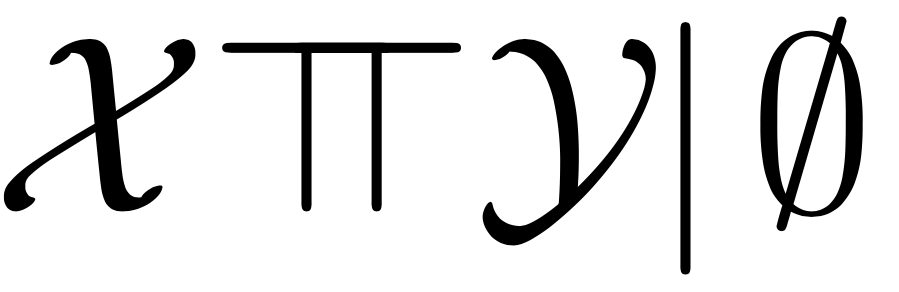
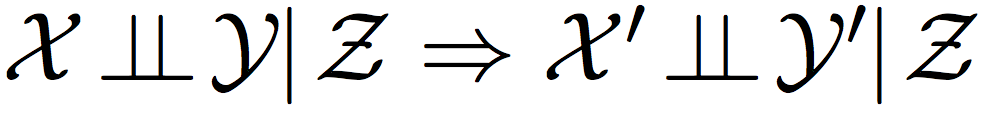
\Leftrightarrow

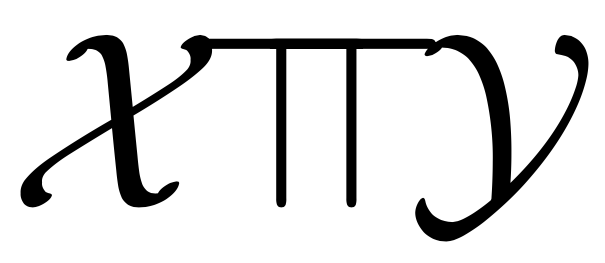
Нетранзитивность независимости

?

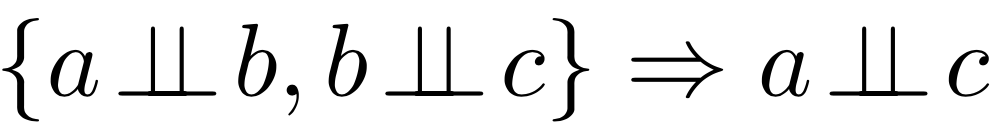
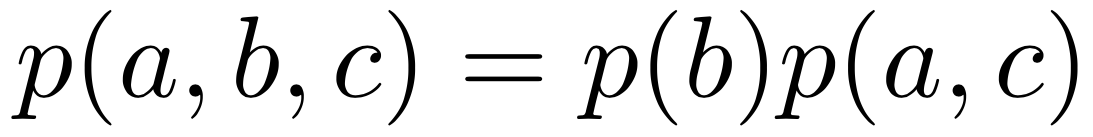
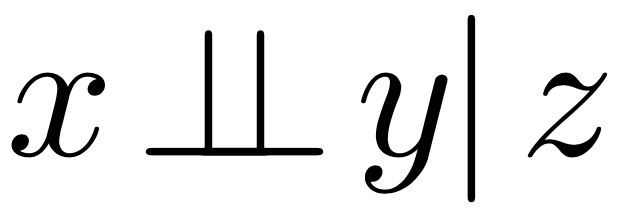
не влечёт

Probabilistiс reasoning

  1. Дан набор случайных величин \(X = \{x_1, \ldots x_n\}\)
  2. Известны некоторые условные вероятности
  3. Вводится evidence — значения для \(X' \subseteq X\)
  4. Из Bayes' rule выводятся целевые значения

Probabilistiс reasoning

Probabilistiс reasoning

Probabilistiс reasoning

Prior & posterior

generative model

prior destribution

posterior destribution

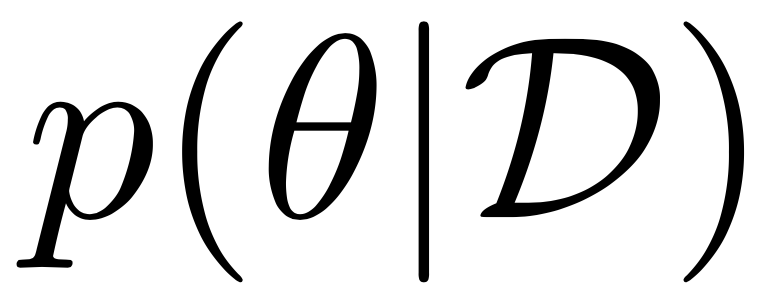
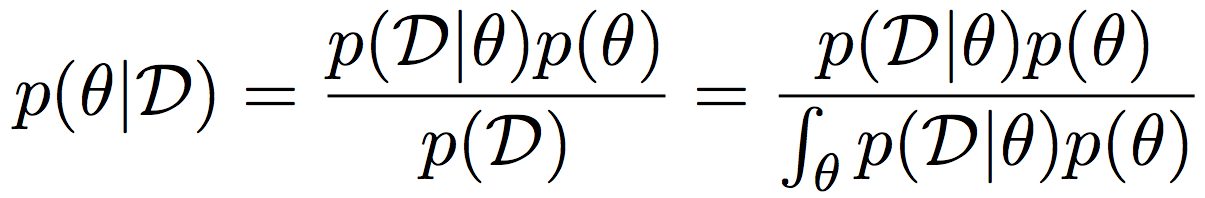
Графы

G = (V, E)

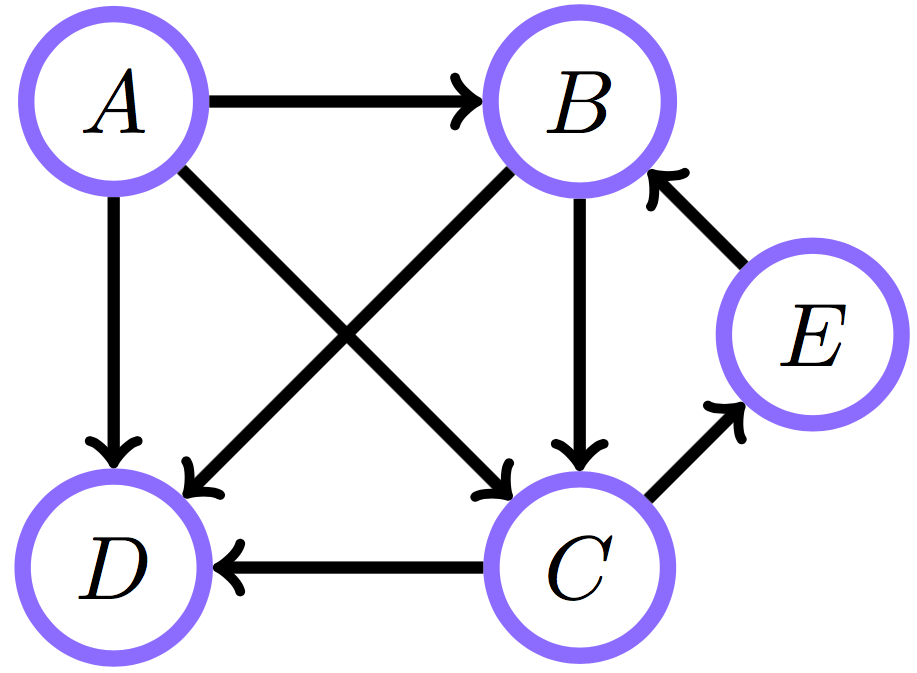
ориентированные

E = \{(v, u) | v, u \in V\}

неориентированные

E = \{\{v, u\} | v, u \in V \}
w_1
w_2
w_3
w_4

Отношения вершин в графе

  1. Дети и родители
  2. Предки и потомки
  3. Соседи и семья
  4. Markov blanket

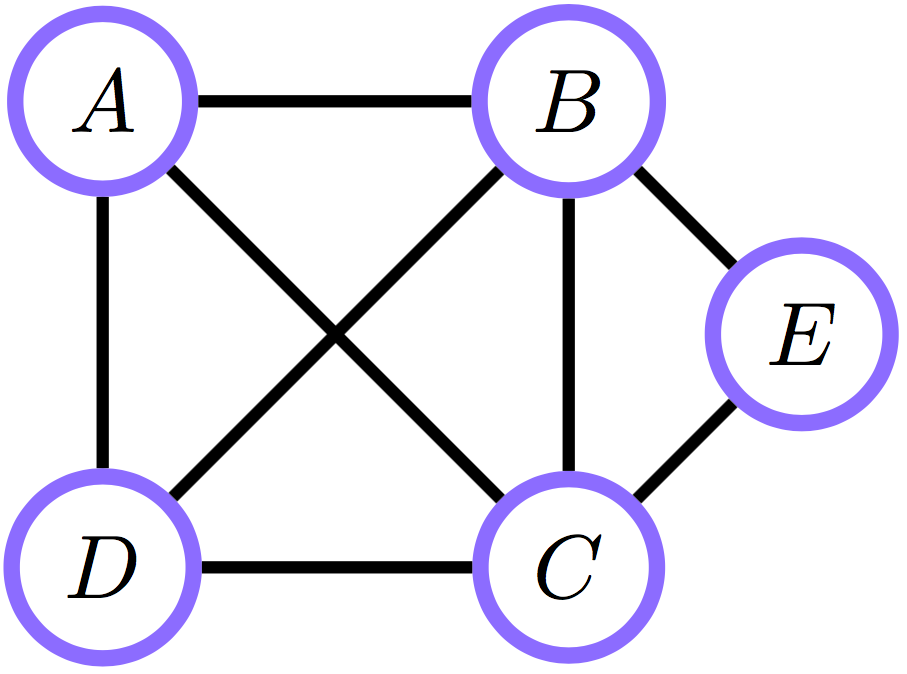
Графы

  1. Пути, циклы и хорды
  2. DAG

Клики

  1. clique
  2. cliquo
  3. Попарная зависимость

Связность

  1. connected graph
  2. singly / multiply connected graph
  3. spanning tree

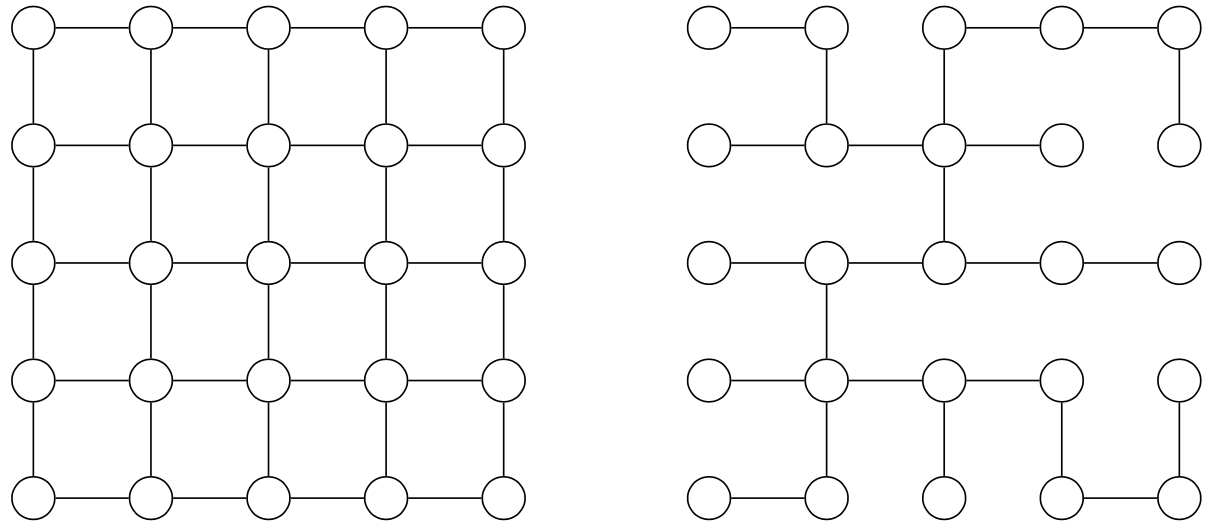
Kruskal's algorithm

G
1
2
3
d_4

Жадное добавление рёбер

по возрастанию веса

Время работы:

\(\mathcal{O} (|E| \, log |V|) \)

Prim's algorithm

G

Постепенное увеличение

связного дерева

Время работы:

\(\mathcal{O} (|E| \, log |V|) \), \(\mathcal{O} (|V|^2) \)

Матрица смежности

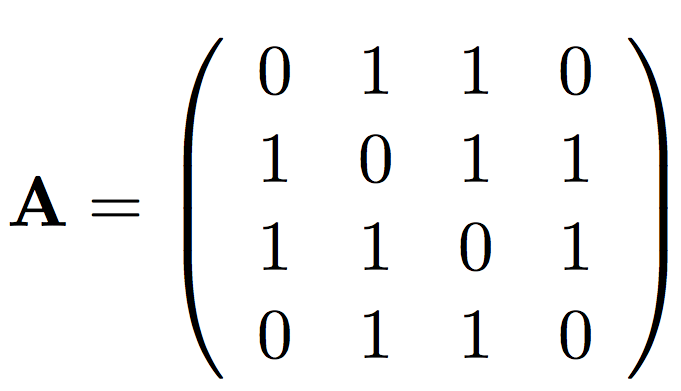
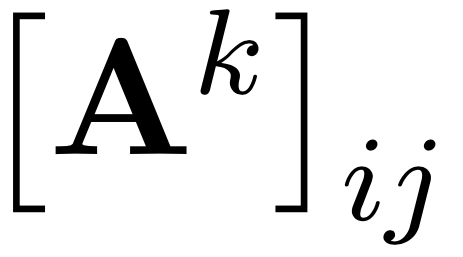
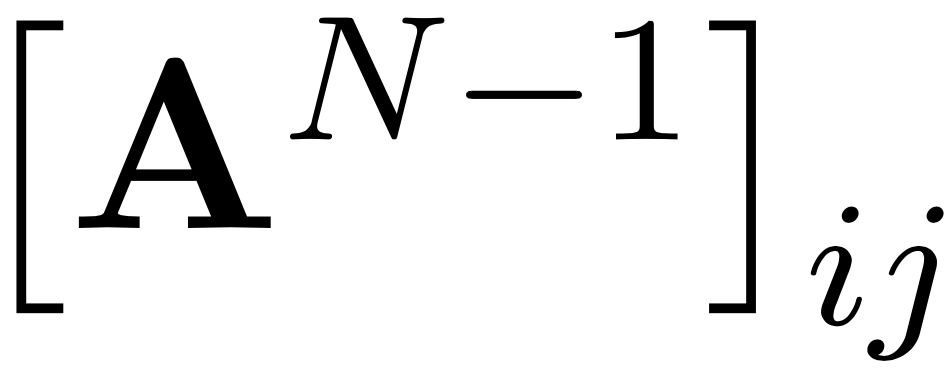
= количеству путей длины \(k\) между \(i, j\)

\neq 0 \Leftrightarrow

существует путь между \(i, j\)

Кликовая матрица

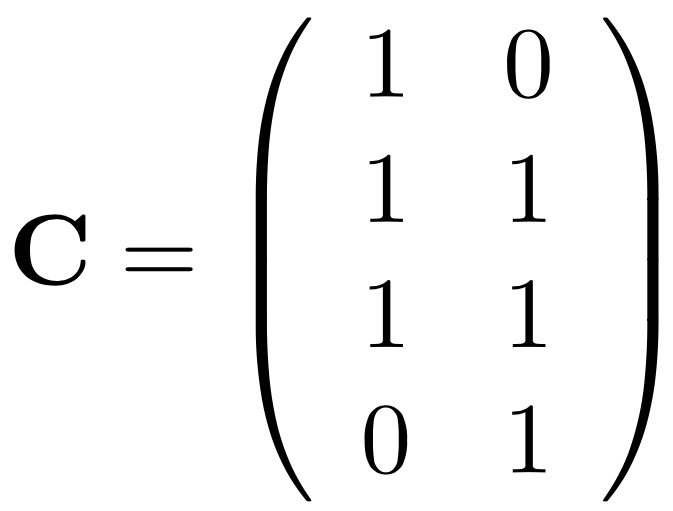
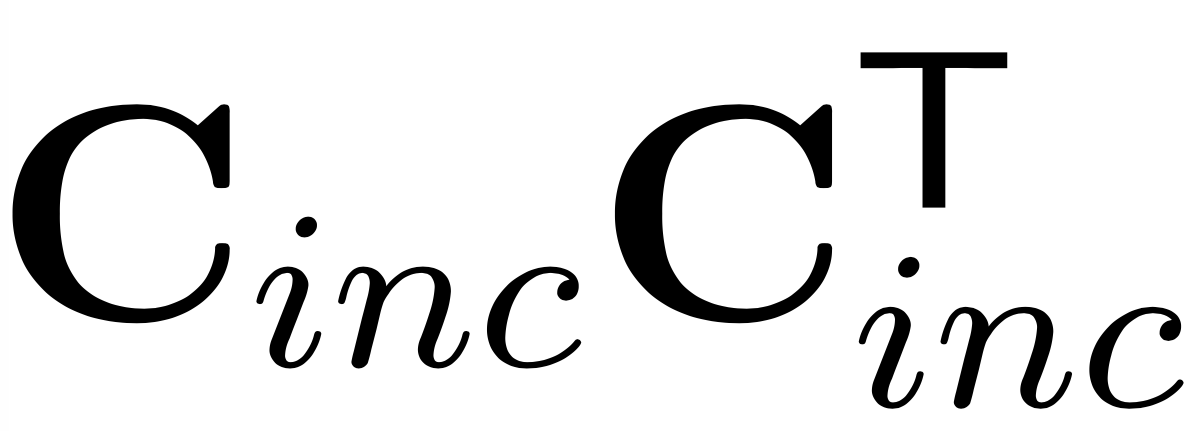
= A'

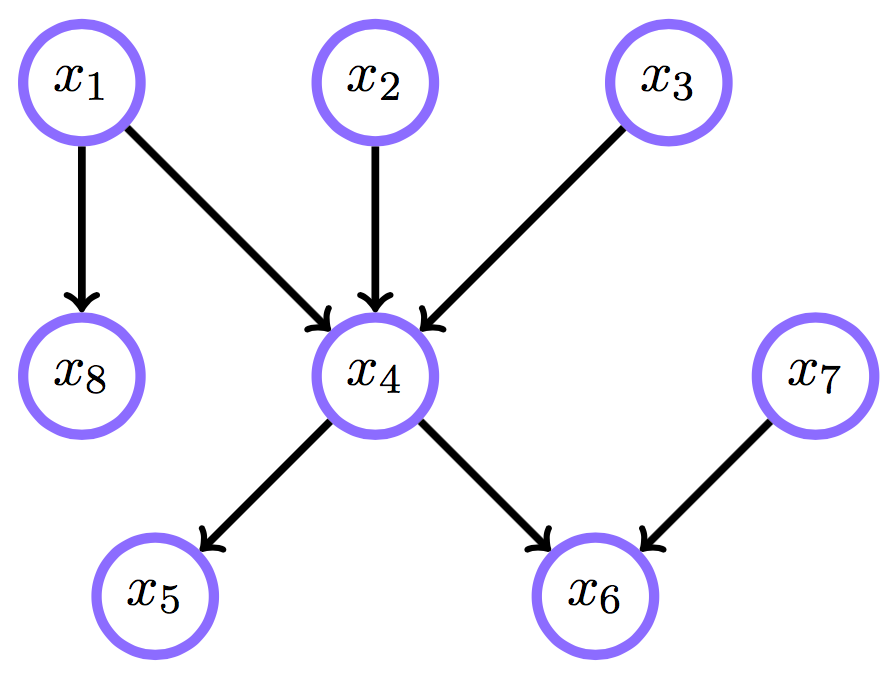
Belief networks

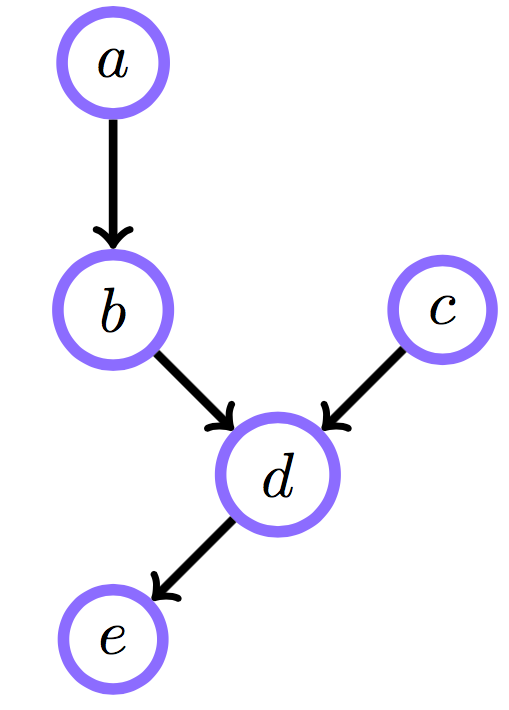
Зависимости между с. в.

Belief networks: пример

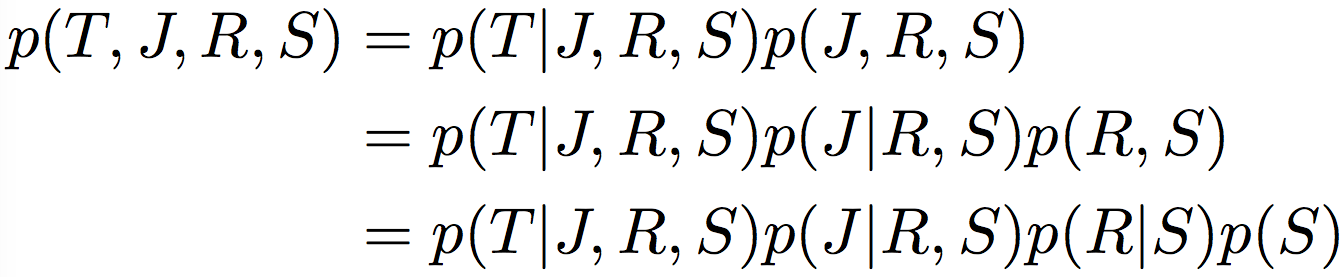
p(S = 1 | T = 1) = \, ?
p(S = 1 | T = 1, J = 1) = \, ?

Belief networks: пример

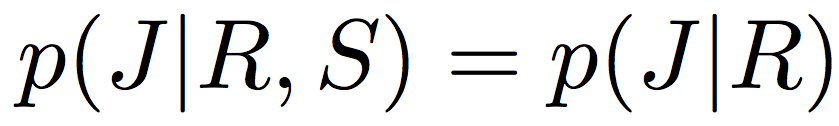
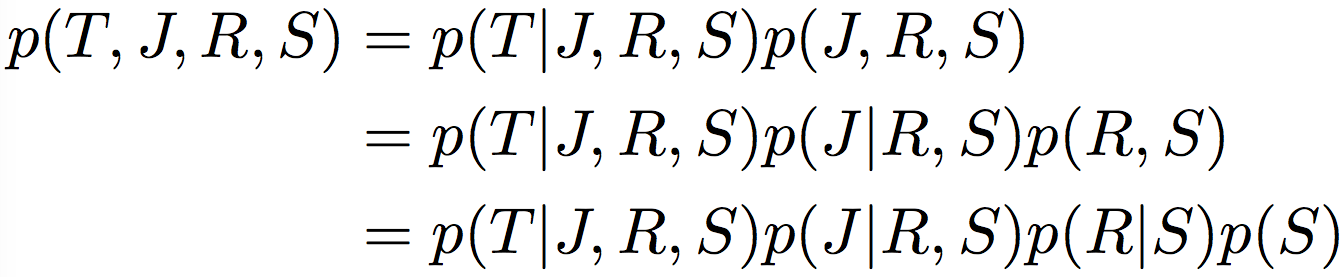
Belief networks: пример

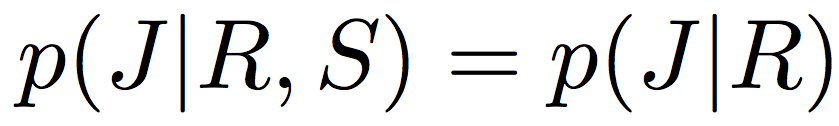
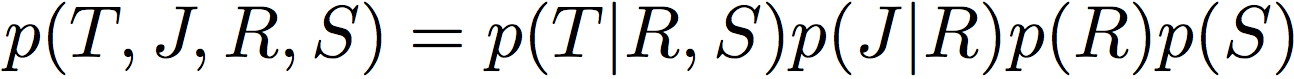
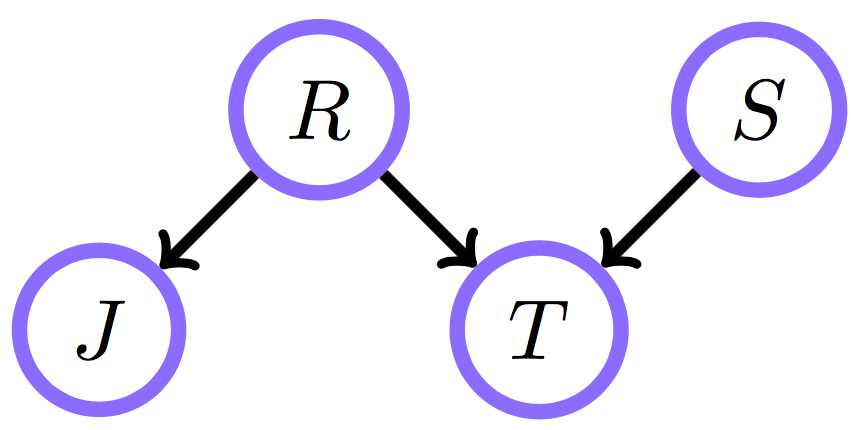
Belief networks: пример

Belief networks: пример

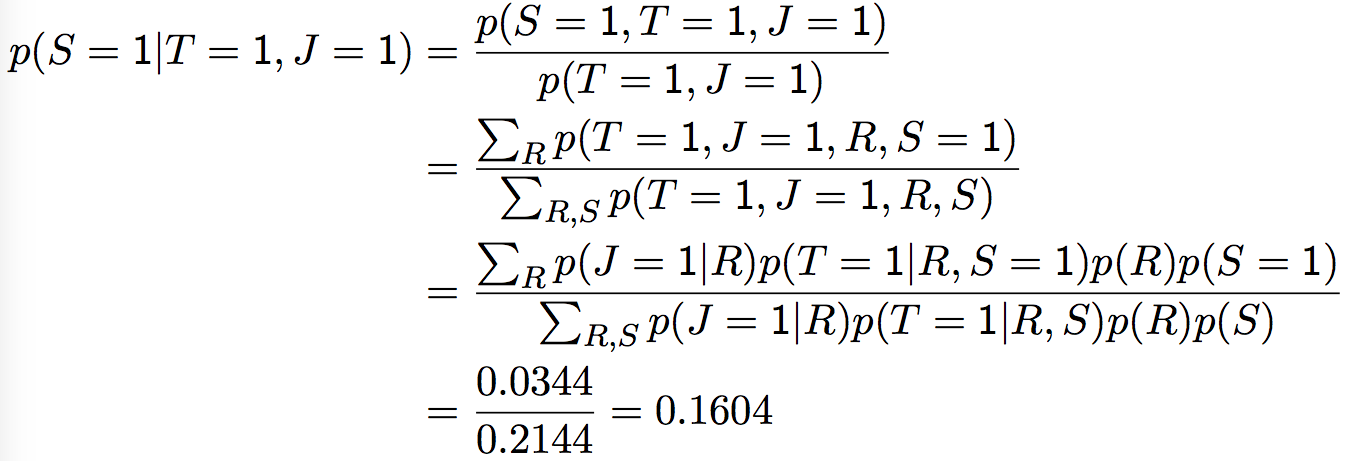
Существуют алгоритмы для подобных вычислений!

Belief networks: определение

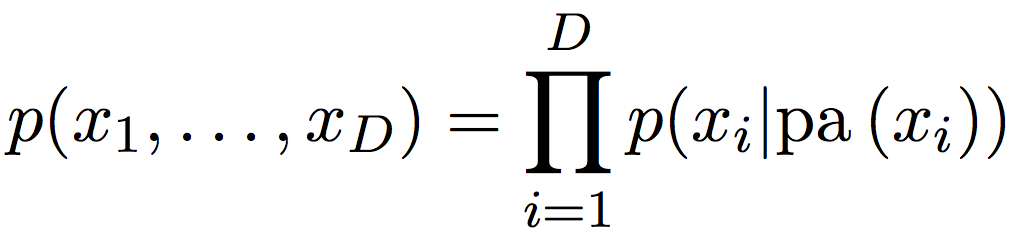
где \(pa(x_i)\) — родители \(x_i\)

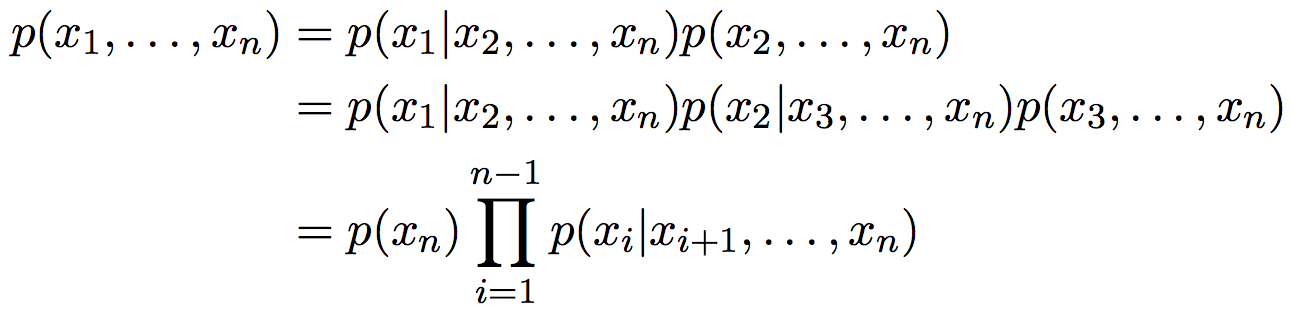
— cascade form

Belief networks: порядок переменных

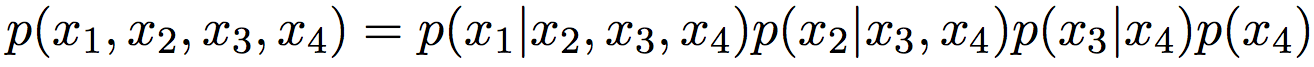
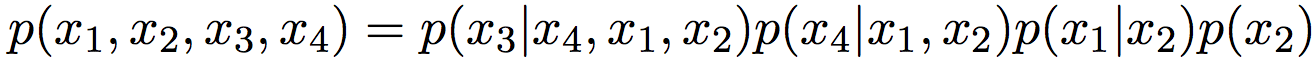
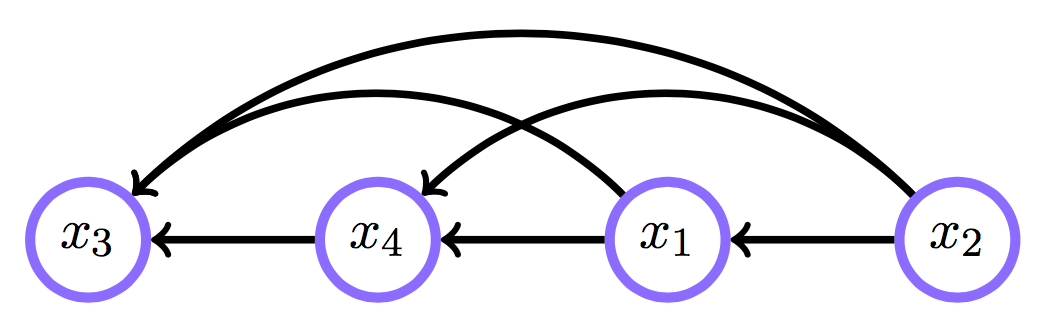
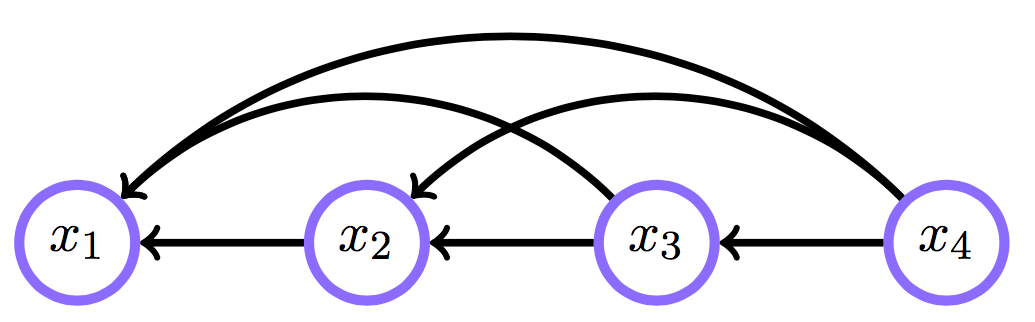
Belief networks: порядок переменных

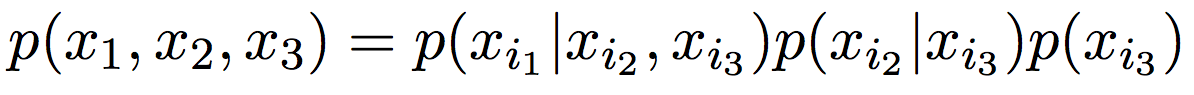
удалим ребро \(x_1\) — \(x_2\):

Evidence 

hard evidence

\(y = a\)

uncertain evidence

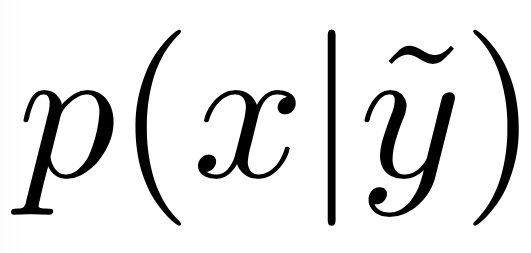
p(y = a, y = b, y = c) = (0.1, 0.6, 0.3)
=

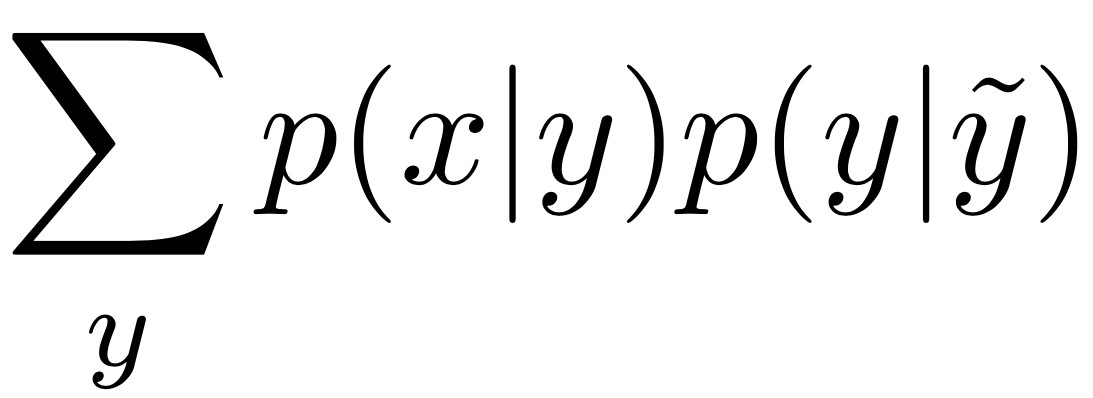
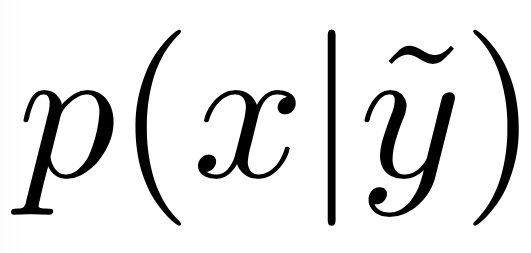
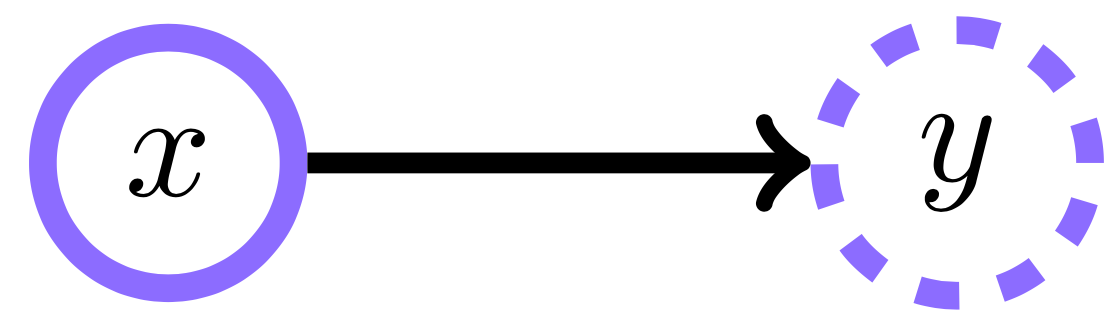
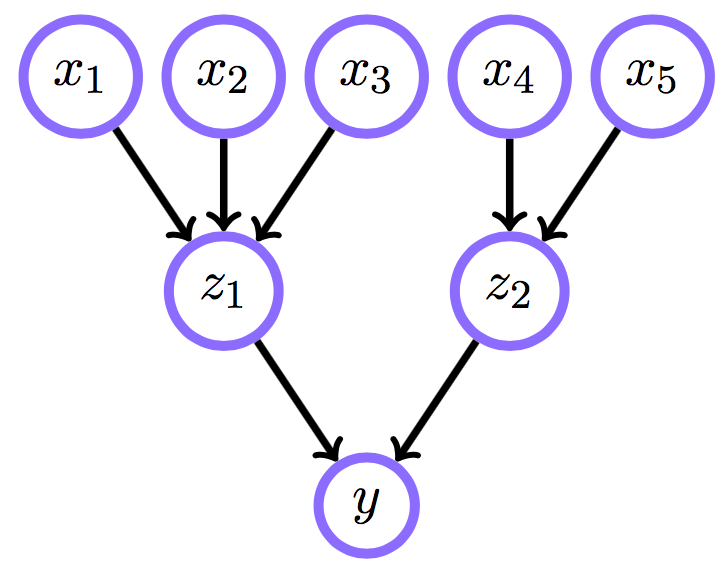
Условная независимость для Markov blanket

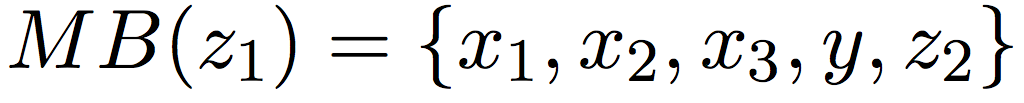
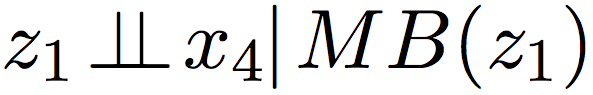
Спасибо за внимание! 

Chapter 1: Inference in Probabilistic Models

By Michael Slabodkin

Made with Slides.com

Chapter 1: Inference in Probabilistic Models

Chapter 1 of «Bayesian Reasoning and Machine Learning»

  • 110

More from Michael Slabodkin