Chapter 11:
Learning with Hidden Variables &
Expectation-Maximisation Algorithm
slabod@, 15.06.2018
Hidden Variables and Missing Data
Variables
visible
missing
hidden
latent
Hidden Variables: complications




— просто считать, факторизация
— сложно считать, нет факторизации
Model of visibility





The missing at random assumption



информация о параметре только в

missing completely at random:
The missing at random assumption


Not missing at random

Maximum likelihood
-
\(x = (v, h)\)
-
MAR
- maximising

неоднозначность решения:



Expectation Maximisation: Variational EM
Идея: нижняя оценка из KLD




\Rightarrow
\Rightarrow
Expectation Maximisation: many data points





\Rightarrow


\Rightarrow
\Rightarrow
Expectation Maximisation: algorithm




Идея: оптимизировать оценку
Expectation Maximisation: algorithm

Expectation Maximisation: algorithm




Идея: оптимизировать оценку
оптимум:

максимизируется только energy
Локальный максимум

Локальный максимум

Локальный максимум


Правдоподобие увеличивается!


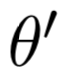



\Rightarrow
Правдоподобие увеличивается!




\Rightarrow
\Rightarrow

(*) +
(*)
\Rightarrow
Belief networks: example



Belief networks: example

Belief networks: example

Belief networks: general case
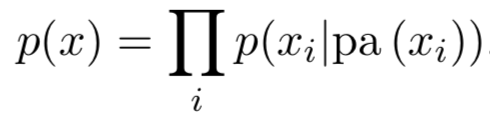





\(E = \)
Belief networks: general case




\(E = \)
Belief networks: general case



\(E / N = \)
= \sum\limits_i \langle \text{KL}(\ldots, \ldots)\rangle_{q_t(\text{pa}(x_i))}
Belief networks: general case




Belief networks: general case algorithm

Convergence

EM for Markov networks




Обобщения EM: partial M-step

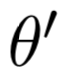

\Rightarrow
Не обязательно искать глобальный оптимум

Обобщения EM: partial E-step




q \in
Вычислительная сложность
\Rightarrow
Обобщения EM: partial E-step

q \in
\Rightarrow






\Rightarrow
Failure case for EM







\Rightarrow
\Rightarrow
Gradient methods



Спасибо за внимание!
\int\limits_T q \, dt
Chapter 11
By Michael Slabodkin
Chapter 11
Chapter 11 of «Bayesian Reasoning and Machine Learning»
- 161



