TD 10 - The Last One
Let's play Chess
| Position |
|---|
|
- col : char // La colonne de la position - lig : int // La ligne de la position |
|
+ Position(char,int) // Construit une position + getCol() : char // Renvoie la lettre de colonne de la position + getLig() : int // Renvoie le numéro de ligne de la position + toString(): String // Renvoie la position en texte (par exemple "a1") |
Visibilité (public, private ...)
Attributs
Constructeur
Méthode
Nom de la classe
Type du paramètre
Type du retour
public class Position {
/** Nom de la colonne. */
private final char col;
/** Numéro de la ligne. */
private final int lig;
/**
* Constructeur
* @param col est le nom de la colonne de la position
* @param lig est le numéro de la ligne de la position
*/
public Position(char col, int lig) {
this.col = col;
this.lig = lig;
}
public char getCol() {
return col;
}
public int getLig() {
return lig;
}
@Override
public String toString() {
return Character.toString(col) +lig ;
}
}
Question 2. Classe Echiquier
On propose de représenter l’échiquier par un tableau à 2 dimensions de pièces (un type Piece sera mis en place dans la suite de l’exercice). Un tel tableau à 2 dimensions se déclare ainsi :
Ensuite, l’accès à l’un de ses éléments situé dans la case « ligne i, colonne j » s’écrit tPieces[i][j]
Écrire la déclaration (en-tête de la classe et attributs) ainsi que le constructeur de la classe Echiquier qui prépare un plateau sans aucune pièce. On considérera qu’une case inoccupée contiendra la valeur null.
Piece[][] tPieces = new Piece[8][8]; // 8 lignes et 8 colonnesQuestion 2. Classe Echiquier
On propose de représenter l’échiquier par un tableau à 2 dimensions de pièces (un type Piece sera mis en place dans la suite de l’exercice). Un tel tableau à 2 dimensions se déclare ainsi :
public class Echiquier {
/** Les pieces de l'échiquier. */
private Piece[][] tPieces;
public Echiquier() {
tPieces = new Piece[8][8];
}
}Question 3. Méthode placer
Écrire la méthode boolean placer(Piece pi, Position po) qui place la pièce pi à la position po (vide ou non) dans l’échiquier et qui indique en retour si l’opération a pu être réalisée.
Remarques : on veillera à faire correspondre la position a1 à la 1re ligne, 1re colonne (d’indices numérotés 0 dans un tableau Java). Une solution possible est d’écrire une méthode auxiliaire qui convertit une lettre en numéro de colonne pour le tableau.
public boolean placer(Piece pi, Position po) {
if (po.getLig() > 0 && po.getLig() <= 8) {
try {
tPieces[po.getLig() - 1][convertir(po.getCol())] = pi;
return true;
} catch (Exception e) {
return false;
}
} else { return false; }
}
private int convertir(char c) throws Exception {
switch (c) {
case 'a':
return 0;
case 'b':
return 1;
case 'c':
return 2;
case 'd':
return 3;
case 'e':
return 4;
case 'f':
return 5;
case 'g':
return 6;
case 'h':
return 7;
default:
throw new Exception("Colonne inconnue");
}
}Question 4. Méthode d’accès
Écrire la méthode Piece get(Position po) qui fournit en résultat la pièce de la position indiquée, ou null si cela n’est pas possible.
/**
* Recupération d'une pièce à partir d'une position
* @param po est la position
* @return la pièce située à la position po
*/
public Piece get(Position po){
if(po.getLig() > 0 && po.getLig() <= 8){
try {
return tPieces[po.getLig() - 1][convertir(po.getCol())];
} catch (Exception e) {
return null;
}
} else {
return null;
}
}
Question 5. Affichage
Écrire la méthode String toString() de la classe Echiquier qui produira le genre de résultat suivant en considérant que la classe Piece dispose d’une méthode toString produisant l’affichage d’une pièce.
Exemple pour l’échiquier de la figure du départ :
a b c d e f g h
8 r n b q k b n r 8
7 p p p p p p p p 7
6 . * . * . * . * 6
5 * . * . * . * . 5
4 . * . * . * . * 4
3 * . * . * . * . 3
2 P P P P P P P P 2
1 R N B Q K B N R 1
a b c d e f g hRemarques : on considérera que dans Piece il existe une méthode toString produisant l’affichage de la pièce en une lettre comme ci-dessus (en minuscule pour les noires, en majuscule pour les blanches), et on séparera chaque pièce affichée par un espace.
public String toString(){
// Entete pour les colonnes
String result = " a b c d e f g h \n";
// On parcourt toutes les lignes de l'échiquier
for(int lig=7; lig >= 0; lig --){
// On affiche le numéro de la ligne
result += lig;
// Pour chaque ligne on parcourt les colonnes
for(int col=0; col < 8; col++){
Piece pi = tPieces[lig][col];
// S'il n'y a pas de pièces sur la position
if(pi == null){
// Si la somme ligne + colonne est paire => case blanche
if((lig + col) % 2 == 0){
result += " .";
} else {
// la case est noire
result += " *";
}
} else {
// S'il existe une pièce, on l'affiche
result += " " + pi;
}
}
result += " " + lig + "\n";
}
result += " a b c d e f g h \n";
return result;
}Question 6. Piece
On souhaite mettre en place le type général Piece, dont découlera ensuite chacun des types particuliers : Roi, Reine, Fou, Cavalier, Tour et Pion.
On souhaite que ce type général mémorise l’information de couleur (pour permettre de savoir si la pièce est blanche ou noire) et que de plus il garantisse que les méthodes publiques String toString(), boolean déplaçable(Position p1, Position p2) et void déplacer(Position p1, Position p2, Echiquier e) seront disponibles.
Écrire en Java votre proposition pour Piece.
public abstract class Piece {
/** true is la pièce est noire, false sinon. */
public boolean black;
public Piece(boolean black){
this.black = black;
}
public abstract String toString();
/**
*
* @param p1 position de départ
* @param p2 position d'arrivée
* @return vrai si la piece peut être déplacée de p1 vers p2
*/
public abstract boolean déplacable(Position p1, Position p2);
/**
* Déplace la pièce de p1 vers p2 sur l'échiquier e.
* @param p1 position de départ
* @param p2 position d'arrivée
* @param e est l'échéquier
*/
public abstract void déplacer(Position p1, Position p2, Echiquier e);
}Question 7. Roi
Écrire entièrement la classe Roi, dont les déplacements peuvent se faire d’une case tout autour de lui comme illustré par les cases cochées autour du roi sur la figure qui suit (on ignorera ici les règles précises qui interdisent certains déplacements par mise en échec, ou les cases déjà occupées par notre camp) :
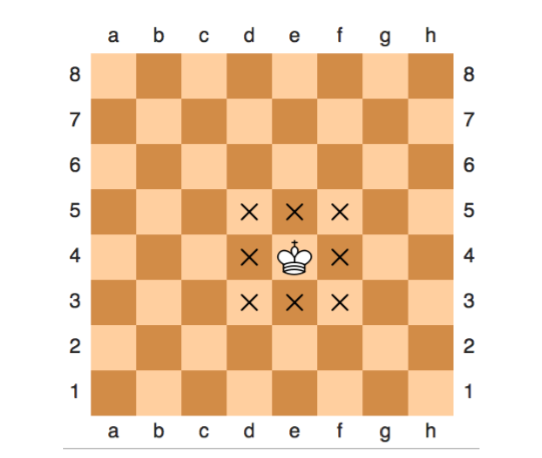
Figure 2 – Les 8 cases accessibles lorsque le roi se déplace
public class Roi extends Piece{
public Roi(boolean black) {
super(black);
}
@Override
public String toString() {
if(black){ return "R"; }else { return "r"; }
}
@Override
public boolean déplacable(Position p1, Position p2) {
try {
return Math.abs(p2.getLig() - p1.getLig()) <= 1
|| Math.abs(Echiquier.convertir(p2.getCol())
- Echiquier.convertir(p1.getCol())) <= 1;
} catch (Exception e) {
return false;
}
}
@Override
public void déplacer(Position p1, Position p2, Echiquier e) {
if(this.déplacable(p1, p2)){
e.placer(null, p1);
e.placer(this, p2);
}
}
}
Question 8. Diagramme de classes UML
Résumer les classes écrites jusqu’à ce point dans un diagramme de classes complet.
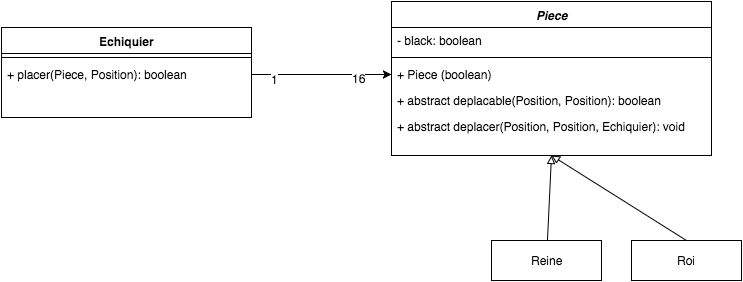
Question 9. Plus de tableau
On remarque que le tableau représentant l’échiquier est au mieux rempli à 50 % (en début de partie) et que peu à peu il se vide, rendant inutiles toutes ces cases inoccupées.
En choisissant une des collections génériques de Java qui vous paraît appropriée pour mieux faire qu’un tableau, redéfinir la partie déclaration d’attribut(s), constructeur et méthode get de la classe Echiquier.
import java.util.HashMap;
import java.util.Map;
public class Echiquier2 {
private Map<Position, Piece> mapPieces;
public Echiquier2(){
mapPieces = new HashMap<Position, Piece>();
}
/**
* Recupération d'une pièce à partir d'une position
* @param po est la position
* @return la pièce située à la position po
*/
public Piece get(Position po){
return mapPieces.get(po);
}
}Question 10. Exceptions
Renvoyer null quand la méthode get ne peut pas répondre, ou bien laisser void en résultat de la méthode déplacer quand un déplacement est impossible ne semble pas très approprié pour imposer aux instructions fautives de gérer proprement ces erreurs possibles.
Définir complètement une classe d’exception nommée ExceptionPosition, et proposer une réécriture de get ainsi que déplacer, utilisant cette exception.
public class ExceptionPosition extends Exception{
public ExceptionPosition(String message){
super(message);
}
} /**
* Déplacer la pièce de p1 vers p2.
* @param p1 est la position de départ
* @param p2 est la position d'arrivée
* @param e est l'échiquier
* @throws ExceptionPosition lorsque le déplacement n'est pas possible
*/
public void déplacer2(Position p1, Position p2, Echiquier e)
throws ExceptionPosition {
if(this.déplacable(p1, p2)){
e.placer(null, p1);
e.placer(this, p2);
} else {
throw new ExceptionPosition(
this + " ne peut pas être déplacée de "+p1+ " vers "+p2);
}
}
/**
* Recupération d'une pièce à partir d'une position
* @param po est la position
* @return la pièce située à la position po
*/
public Piece get2(Position po) throws ExceptionPosition{
Piece piece = mapPieces.get(po);
if(piece == null){
throw new ExceptionPosition(
" Il n'y pas de pièce sur la position "+po);
}
return piece;
}Exercice 2 : Réutilisation de classe (≈ 20 minutes)
Quand on travaille sur un graphe, il est parfois nécessaire de le simplifier. L’algorithme de Kruskal est un algorithme qui prend en entrée un graphe connexe1 non orienté et valué par des poids, et qui calcule pour ce graphe un arbre (graphe sans cycle) qui relie tous les sommets du graphe par un ensemble d’arêtes dont le poids total est minimale. Cet ensemble d’arêtes est appelé arbre couvrant de poids minimal.
Soit G = (V,E) un graphe avec un ensemble de sommets V et un ensemble d’arêtes E (chaque arête est un triplet (v,d,v’), où v et v’ sont des sommets et d est un poids (on supposera que ce poids est un entier).
L’algorithme de Kruskal sur G renvoie un graphe sans cycle G’=(V, E’), tel que
-
Pour tout (v,d,v’) dans E’, le graphe (V , E’-{(v,d,v’)} ) n’est plus connexe
(aucune arête du résultat ne peut être retirée sans dommage)
-
Pour tout autre graphe connexe sans cycle G’’=(V,E’’), la propriété suivante est vérifiée :
𝑑≤𝑑 (!,!,!!)∈!! (!,!,!!)∈!!!
(le poids de l’ensemble des arêtes choisies est minimal)
L’algorithme de Kruskal peut être utilisé, par exemple, pour déterminer comment relier des villes entre elles par le réseau routier le moins cher à entretenir.
-
1 Une composante connexe est un groupe dont tous les éléments sont connexes, c’est-à-dire qu’il existe toujours un chemin pour relier 2 éléments. Un graphe connexe est alors un graphe où tous les sommets sont dans une seule et même composante connexe.
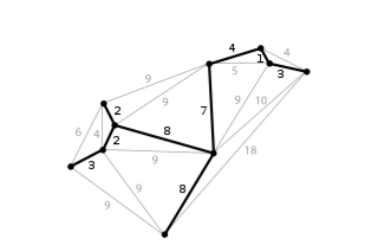
Question 11.
Implémenter la méthode findCC de la classe Kruskal.
/**
* Identifie la CC d’un sommet.
*
* @param e le sommet considéré
* @return le plus petit no contenu dans la liste de sommets avec lesquels e
* est connexe
*/
public int findCC(int e) {
List<Integer> sommetsConnectes = connectedComponents.get(e);
return Collections.min(sommetsConnectes);
}
Question 12.
Implémenter la méthode unionCC de la classe Kruskal.
/** Calcule l’union des CC de 2 sommets. Après l’union, les CC des 2 sommets indiqueront les mêmes nos.
* @param v Le premier sommet
* @param u Le second sommet
*/
public void unionCC(int u, int v) {
ArrayList<Integer> union = new ArrayList<Integer>(connectedComponents.get(u));
for(Integer sommet : connectedComponents.get(v)){
if(!union.contains(sommet)){
union.add(sommet);
}
}
connectedComponents.put(u, union);
connectedComponents.put(v, union);
}Question 13.
Indiquer et justifier quel algorithme de tri vu en cours semble le plus adapté au a) et lequel au b).
a) merge sort (tri fusion) qui fonctionne aussi bien sur les structures quasi triées
b) quick sort qui est le plus efficace (sur les structures non triées)
Question 14.
On supposera, pour l’exercice, que l’on peut affirmer qu’un tableau de taille n est presque trié s’il est log(n)-quasi-trié. On supposera qu’il existe une méthode boolean quasiSorted(int m, int[ ] T), qui indique si un tableau est m-quasi-trié. Proposer un algorithme qui teste si le tableau est presque trié puis appelle l’algorithme de tri le plus adapté (d’après votre réponse précédente).
public static int[] sort(int[] tab){
int indice = (int) Math.log(tab.length);
if(quasiSorted(indice, tab)){
return mergeSort(tab);
}else {
return quickSort(tab, 0, tab.length -1);
}
}Question 15.
En faisant l’hypothèse (optimiste) que quasiSorted est en O(n), quelle est la complexité au pire de l’algorithme de la question précédente ? Sa complexité en moyenne ?
Au pire c'est O(n) (celle de quasiSorted) + max (pire de merge sort, pire de quick sort) => O(n + n2)
Au moyenne c'est O(n) (celle de quasiSorted) + moyenne (quick sort, merge sort) => O(n + nlog(n))
Question 16.
Écrire une méthode int findPermutationBound(int[ ] T), qui renvoie le plus petit entier m tel que T est m- quasi-trié. Notons que si T est i-quasi-trié, alors il est i+1-quasi-trié, mais l’inverse est faux.
Donner la complexité au pire de votre méthode.
public static int findPermutationBound(int[ ] tab){
int permutationBound = 0;
for(int i = 0; i<tab.length; i ++){
int value = tab[i];
int precedent = 0;
for(int j=0; j<tab.length; j ++){
// On cherche l'entier qui précède tab[i]
if(j != i && tab[j] > precedent && tab[j] <= value){
precedent = j;
}
}
int ecart = precedent-i;
if(ecart > permutationBound){
permutationBound = ecart;
}
}
return permutationBound;
}
Complexité au pire O(n2)
Question 17.
Pensez-vous que cette solution est améliorable ? Pourquoi ? Qu’en concluez-vous ?
Améliorable ? On pourrait améliorer la méthode findPermutationBounds en utilisant une technique de tri (plus efficace) et en stockant le déplacement max réalisé
Qu’en concluez-vous ? Que s'il faut trier le tableau pour vérifier s'il est quasi trié et décider ensuite quelle méthode de tri effectuer, alors l'algo de la question 14 n'est pas efficace
INSA 2ième Année - TD10 (1ère version)
By Mickael Lecoq
INSA 2ième Année - TD10 (1ère version)
- 1,819



