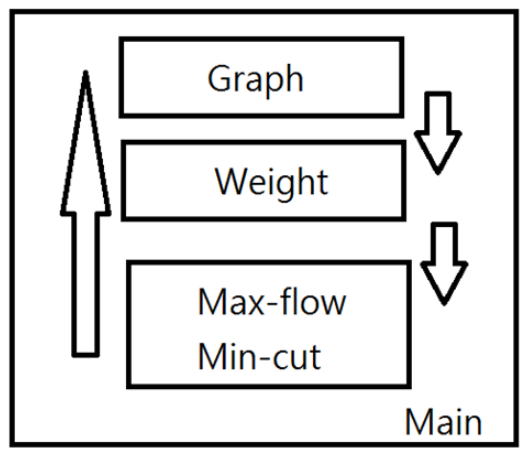
Graph Cut
以 Max-flow Min-cut 為延伸

專題動機及目標
Max-flow Min-cut
The Network Flow Problem
想像水流以穩定的速度從左邊流向右邊
每一個管子會流過多少的水流?
演算法的目的即是為了找出兩點間最大流量
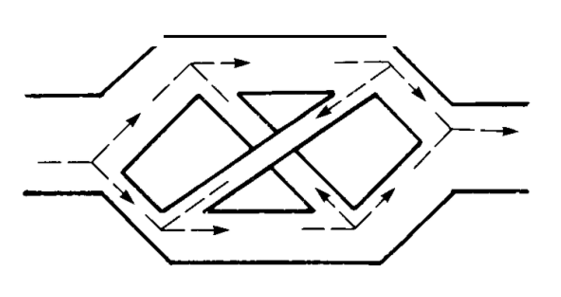
Max-flow
- 從 S 到 T 的流量為最大量,則稱為 Max-flow
- 條件限制
- 流量守恆:流入的量必須大於等於流出的量
- 容量限制:流量必小於等於容量
- 斜對稱:流過去的量必等於流回來的量
Min-cut
- Cut 是一條邊,將一張圖切成兩邊不相交的圖
- 在許多條 Cut 的裡面,總容量最小的這稱為Min-cut
Max-flow Min-cut
- 目前有兩種演算法
- Ford-Fulkerson
- 隨意地找出一條增廣路徑,找出後修正殘餘流量直到找不出增廣路徑為止
-
Edmonds-Karps
- Ford-Fulkerson 的改進
- 利用廣度優先搜尋(BFS)來搜尋增廣路徑
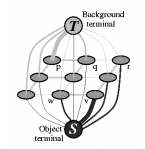
Weight
權重
表達的方式
-
Ⓡ 代表一個被劃紅線的點
-
這是要的(左鍵)
-
-
Ⓑ 代表一個被劃藍線的點
-
這是不要的(右鍵)
-
-
O 這是一般還沒決定前景後景的
ⓇOO
OOO
OOⒷ
被劃紅線的
T
|
0
|
O-weight-Ⓡ-weight-O
|
1
|
S
被劃藍線的
T
|
1
|
O-weight-Ⓑ-weight-O
|
0
|
S

公式
- N 相鄰
- ∝ 正比
- exp 為 指數分配
- dist 為 1 (上下左右)
- I 亮度(灰階)
- σ 標準差
根據
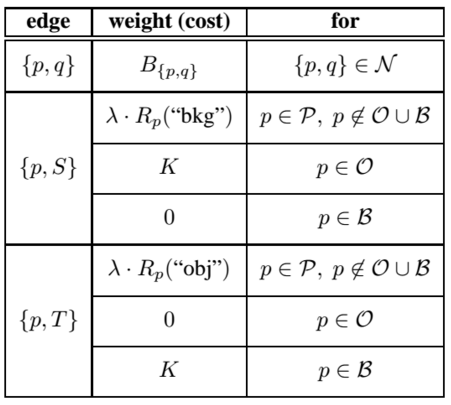
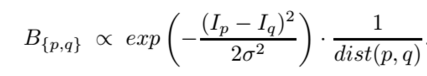
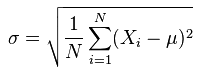
公式
根據
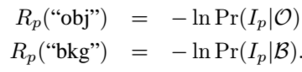

- λ值為可調
- ln 自然對數
- Pr(Ip|O)
公式
- q:{p, q} => q / {p, q}
- p, q 相鄰
- N 鄰近的點
- K 為 1 + (p 週邊權重相加)
根據


程式
原公式
修改後
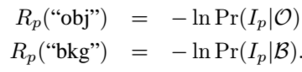
使用者畫的紅點 = R
使用者畫的藍點 = B
Rp(“obj”) = max((|IR-Ip|/dist(R, p))/255)
Rp(“bkg”) = max((|IB-Ip|/dist(B, p))/255)
實際測試
滑鼠狀態顯示
測試滑鼠的區域
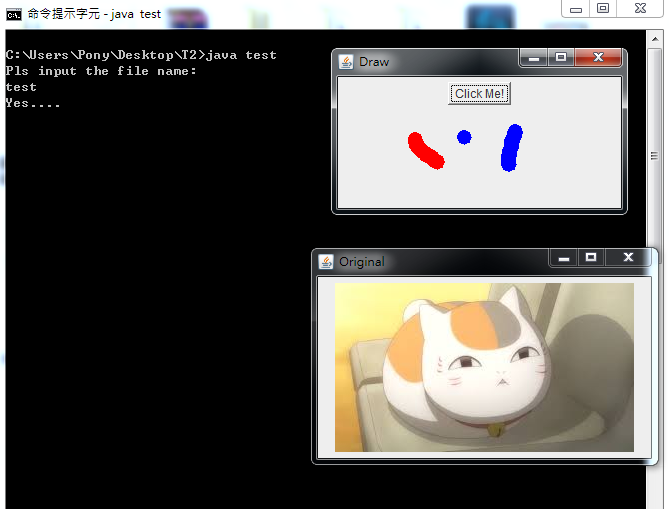
讀取圖片並畫圖的測試
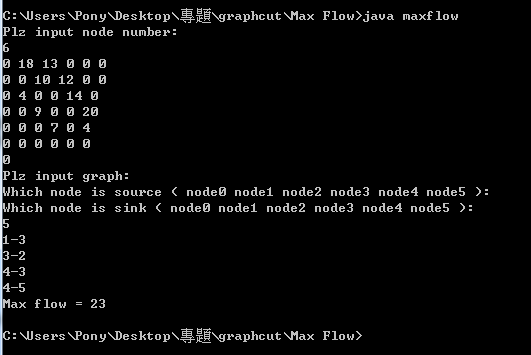
Max-flow Min-cut的測試
結合測試

實際結果
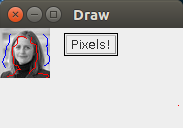
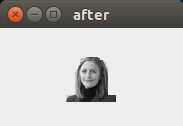
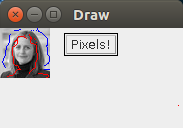
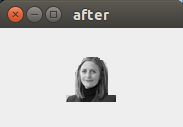
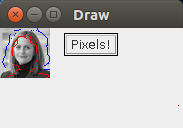
DEMO
未來展望
若是將速度加速到可以把程式放入到影像上面,而不讓使用者感受到很嚴重的延遲,也許能夠實用在視訊通話或是攝影當中,使人能夠隨意的選擇自己的背景。但這首先要克服的是程式執行效率。光要解決這問題,而要達到這目的應該還有一段距離。
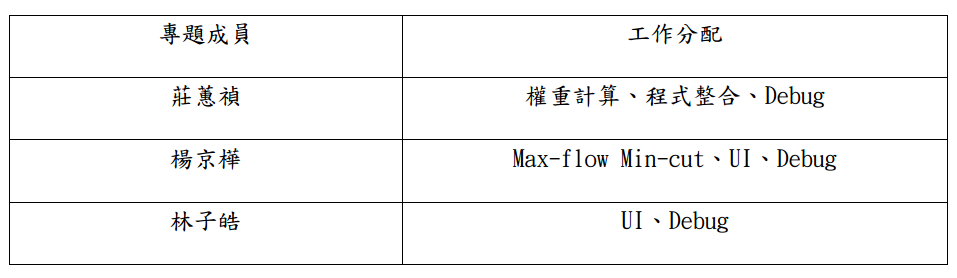
專題分工
graphcut
By Huei-Jhen Jhuang
graphcut
- 974



