CS6015: Linear Algebra and Random Processes
Lecture 28: Probability Space, Axioms of Probability, Designing Probability Functions
Probability Theory
Basics
Laws
Random Var.
Applications
Processes
Counting
Set Theory
Axioms
Union rule
Multiplication Rule
Total Probability Theorem
Bayes' Theorem
Independence
\mathbb{P}: \mathcal{F} \rightarrow [0,1]
X: \mathcal{\Omega} \rightarrow \mathbb{R}
PMF, PDF, CDF
Expectation, Var., Moments
Distributions (~10)
Bayes' Theorem
Independence
Sampling from a distribution
Designing arbitrary probability functions
Estimating Parameters
X_1, X_2, \dots, X_t,\dots
Simple Random Walk
Bernoulli Process
Poisson Process
Markov Process
.... .... ....
Limit Theorems
Markov inequality
Chebychev inequality
Weak Law of large nos.
Central Limit Theorem
The
St
Joint, cond., marginal dist.
(ML)
.... .... ....
Learning Objectives
What is a probability space?
What are the axioms of probability?
What are some simple ways of defining a probability function?
Probability Space
Definitions
\(\Omega\): Sample space (all outcomes)
Event: subsets of \(\Omega\)
Field \(\mathcal{F}\): a subcollection of the set of all subsets of \(\Omega\) such that
if \(A,B \in \mathcal{F}\) then \(A\cap B \in \mathcal{F}\) and \(A\cup B \in \mathcal{F}\)
if \(A \in \mathcal{F}\) then \(A^\mathsf{c} \in \mathcal{F}\)
\(\phi\in \mathcal{F}\)
(empty set)
Why not simply say all subsets of \(\Omega\) ?
(beyond the scope of this course)
Definitions
\(\sigma\)-field \(\mathcal{F}\): A collection of the subsets of \(\Omega\) is called a \(\sigma\)-field if
if \(A_1,A_2, \dots \in \mathcal{F}\) then \(\cup_{i=1}^{\infty} A_i \in \mathcal{F}\)
if \(A \in \mathcal{F}\) then \(A^\mathsf{c} \in \mathcal{F}\)
\(\phi\in \mathcal{F}\)
(empty set)
if \(A_1,A_2, \dots \in \mathcal{F}\) then \(\cap_{i=1}^{\infty} A_i \in \mathcal{F}\)
closed under countable unions & intersections
The power set of \(\Omega\) which contains ALL subsets of \(\Omega\) is obviously a \(\sigma\)-field
Definitions
a probability measure \(\mathbb{P}\) on \(\Omega, \mathcal{F}\) is a function \(\mathbb{P}: \mathcal{F} \rightarrow [0,1] \) satisfying the axioms of probability
The triple \((\Omega, \mathcal{F}, \mathbb{P})\) where \(\mathcal{F}\) is a \(\sigma\)-field, is called a probability space
(we will soon see what these axioms are)
Recap
Experiments
Sample Space
Events
What is the chance of an event?
Goal: Assign a number to each event such that this number reflects the chance of the experiment resulting in that event
(\(\sigma\)-field \(\mathcal{F}\))
The probability function
What are the conditions that such a probability function must satisfy?
(Axioms of Probability)
P(A) = ?
Event
Probability function
The axioms of probability
P(A) \geq 0~\forall A
Axiom 1 (non-negativity)
P(\Omega) = 1
Axiom 2 (normalisation)
Axiom 3 (finite additivity)
If the events are mutually disjoint then
A_1, A_2, \dots, A_n
= \sum_{i=1}^n P(A_i)
P(A_1\cup A_2 \cup \dots \cup A_n)
The axioms of probability
Axiom 3 (finite additivity)
= \sum_{i=1}^n P(A_i)
P(A_1\cup A_2 \cup \dots \cup A_n)
Smallest possible event = one outcome
Compute probabilities of larger events from smaller events






A_1
A_2
A_3
A_4
A_5
A_6
The axioms of probability
Given
P(A_1),P(A_2),P(A_3),P(A_4),P(A_5),P(A_6)
B
: the event that the outcome is an odd no.
C
: the event that the outcome is
P(B) = P(A_1)+P(A_3)+P(A_5)
\geq 5
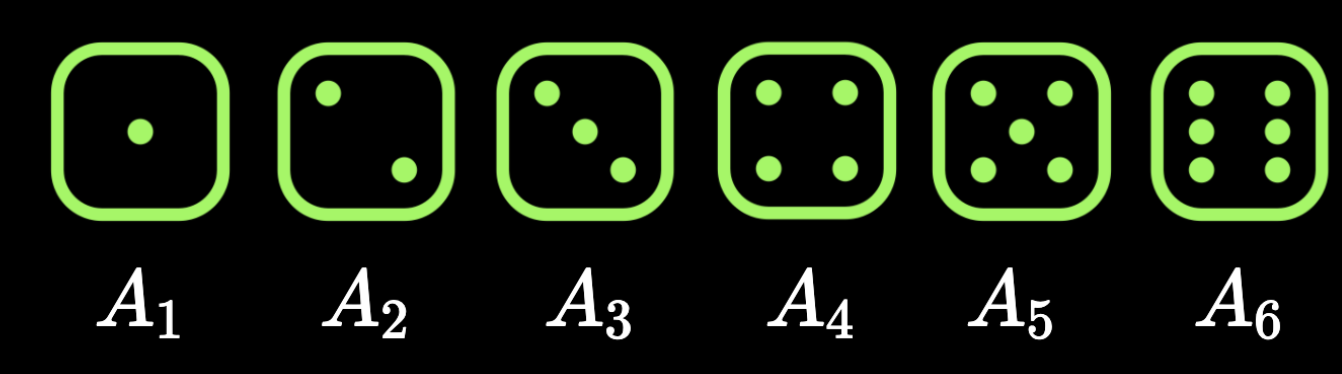
P(C) = P(A_5)+P(A_6)
D
: the event that the outcome is a mult. of 3
P(D) = P(A_3)+P(A_6)
we can compute other probabilities
The probability of an event can be computed as the sum of the probabilities of the disjoint outcomes contained in the event

Some properties of probability
Property 1:
P(A) = 1 - P(A^\mathsf{c})
A \cup A^\mathsf{c} = \Omega

1 = P(\Omega) = P(A \cup A^\mathsf{c}) = P(A) + P(A^\mathsf{c})
\therefore P(A) = 1 - P(A^\mathsf{c})
Property 2:
P(A) \leq 1
P(A) = 1 - P(A^\mathsf{c})
Some properties of probability
Property 3:
P(A \cup B) = P(A) + P(B) - P(A \cap B)

A^\mathsf{c}
P(A \cup B) = P(A \cup (B \cap A^\mathsf{c}))
= P(A) + P(B \cap A^\mathsf{c})
P(B) = P((B \cap A^\mathsf{c}) \cup (B \cap A))
= P(B\cap A^\mathsf{c}) + P(B\cap A)
\therefore P(B\cap A^\mathsf{c}) = P(B) - P(B\cap A)
= P(A) + P(B) - P(B\cap A)
Some properties of probability
Property 4:
\Omega = A_1 \cup A_2 \cup \dots \cup A_n
the sum of the probabilities of all outcomes is equal to 1

P(\Omega) = P(A_1 \cup A_2 \cup \dots \cup A_n) = \sum_{i=1}^n P(A_i)
\therefore \sum_{i=1}^n P(A_i) = 1
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~}
\Omega
Property 5:
P(\phi) = 0
\therefore 1 = P(\Omega) = P(\Omega \cup \phi) = P(\Omega) + P(\phi)
\therefore 1 = 1 + P(\phi) \implies P(\phi) = 0
Examples
Outcomes: {0, 1, 2, 3, 4, 5, 6}

A_0, A_1, A_2, A_3, A_4, A_5, A_6
P(A_0)=0.3, P(A_1)=0.45, P(A_2)=0.12, P(A_3)=0.02, \\ P(A_4)=0.07, P(A_5)=0.01, P(A_6)=0.03
What is the prob. of scoring even no. of runs?
X = A_0 \cup A_2 \cup A_4 \cup A_6
P(X) = P(A_0 \cup A_2 \cup A_4 \cup A_6)
= P(A_0) + P(A_2) + P(A_4) + P(A_6)
Examples
Outcomes: {0, 1, 2, 3, 4, 5, 6}

A_0, A_1, A_2, A_3, A_4, A_5, A_6
P(A_0)=0.3, P(A_1)=0.45, P(A_2)=0.12, P(A_3)=0.02, \\ P(A_4)=0.07, P(A_5)=0.01, P(A_6)=0.03
What is the prob. of scoring less than 5 runs?
X = A_0 \cup A_1 \cup A_2 \cup A_3 \cup A_4
P(X) = P(A_0 \cup A_1 \cup A_2 \cup A_3 \cup A_4)
= P(A_0) + P(A_1) + P(A_2) + P(A_3) + P(A_4)
Examples
Outcomes: {0, 1, 2, 3, 4, 5, 6}

A_0, A_1, A_2, A_3, A_4, A_5, A_6
P(A_0)=0.3, P(A_1)=0.45, P(A_2)=0.12, P(A_3)=0.02, \\ P(A_4)=0.07, P(A_5)=0.01, P(A_6)=0.03
The prob. that the runs will be div. by 2 or 3?
X_1 = \{0, 2, 4, 6\} = A_0 \cup A_2 \cup A_4 \cup A_6
X_2 = \{0, 3, 6\} = A_0 \cup A_3 \cup A_6
X_1 \cap X_2 = \{0, 6\} = A_0 \cup A_6
P(X_1) = 0.3 + 0.12 + 0.07 + 0.03 = 0.52
P(X_2) = 0.3 + 0.02 + 0.03 = 0.35
P(X_1 \cap X_2) = 0.3 + 0.03 = 0.33
P(X_1 \cup X_2) = P(X_1) + P(X_2) - P(X_1 \cap X_2)
\therefore P (X_1 \cup X_2) = 0.52 + 0.35 - 0.33 = 0.54
Examples
The ball bearings manufactured by a factory have two types of defects. Suppose the probability of having Type 1 defect is 0.01, having Type 2 defect is 0.02 and having both is 0.0005
P(A_1)=0.01, P(A_2)=0.03, P(A_1 \cap A_2) = 0.005
P(A_1 \cup A_2)= P(A_1) + P(A_2) - P(A_1 \cap A_2)
What is the prob. that the bearing will have type 1 or type 2 defect ?
= 0.01 + 0.02 - 0.005 = 0.025
A_2
A_1
Examples
The ball bearings manufactured by a factory have two types of defects. Suppose the probability of having Type 1 defect is 0.01, having Type 2 defect is 0.02 and having both is 0.0005
P(A_1)=0.01, P(A_2)=0.03, P(A_1 \cap A_2) = 0.005
P(A_1 \cup A_2)^\mathsf{c}= 1 - P(A_1 \cup A_2)
What is the prob. that the bearing will have neither type 1 nor type 2 defect ?
= 1 - 0.025 = 0.975
A_2
A_1
Designing Probability Functions
Designing Probability Functions
(probability as relative frequency)
Recap
Goal: Assign a number to each event such that this number reflects the chance of the experiment resulting in that event
Required: The probability function must satisfy the axioms of probability
Probability as relative frequency

Karl Pearson tossed a coin 24000 times he observed that the number of heads was 12012
P(H) = \frac{12012}{24000} = 0.5005
We can think of the probability of an event as the fraction of times the event occurs when an experiment is repeated a large number of times

Probability as relative frequency
We can think of the probability of an event as the fraction of times the event occurs when an experiment is repeated a large number of times

P(A_i) = \frac{no.~of~times~the~outcome~is~in~A_i}{total~no.~of~times~the~experiment~was~repeated}
But does such a P() satisfy the axioms of probability?
Probability as relative frequency
P(A_i) \geq 0~?
: ratio of two positive numbers
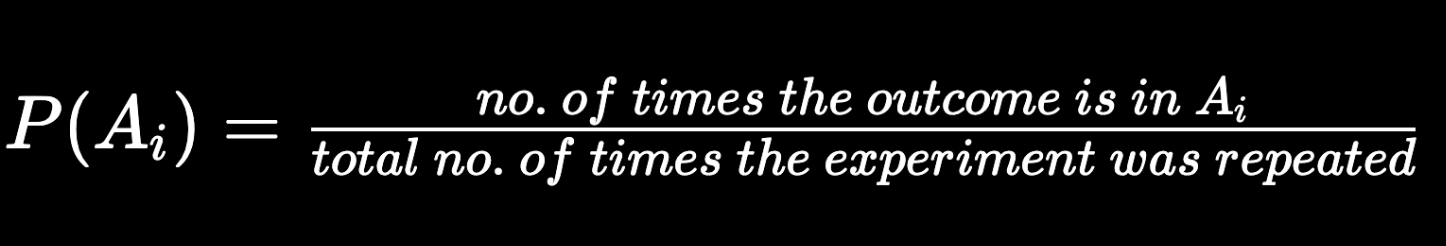
Does P() satisfy the axioms?
P(\Omega)=1~?
P(\Omega) = \frac{no.~of~times~the~outcome~is~in~S}{total~no.~of~times~the~experiment~was~repeated} = 1
\Omega
P(A_1 \cup A_2) = P(A_1)+ P(A_2)~?
P(A_1 \cup A_2) = \frac{k_1 + k_2}{k} = \frac{k_1}{k} + \frac{k_2}{k}
= P(A_1)+ P(A_2)
A_1
A_2
Probability as relative frequency
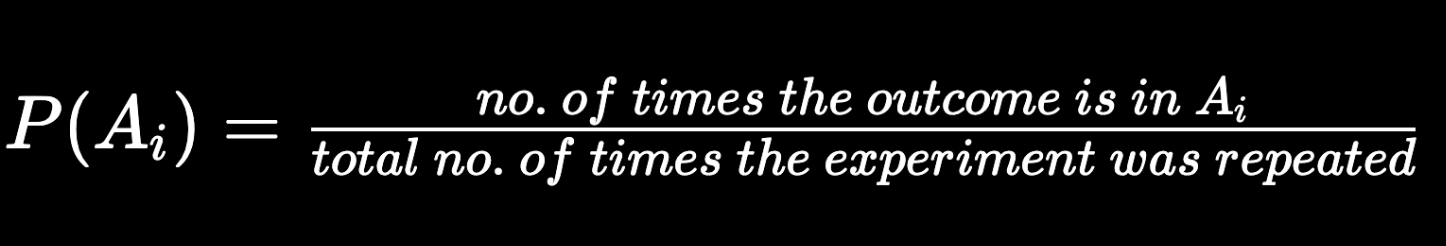
Does P() satisfy the axioms?
\Omega
P(A_1 \cup A_2) = P(A_1)+ P(A_2)~?
|\Omega| = n \implies 2^n~subsets \implies 2^n~events
A_1, A_2, A_3, \dots, A_n
Suppose are the outcomes
Every event is a union of these outcomes
If the frequencies of are known then the probability of any event can be computed
A_1, A_2, A_3, \dots, A_n
(axioms are about events)
Examples
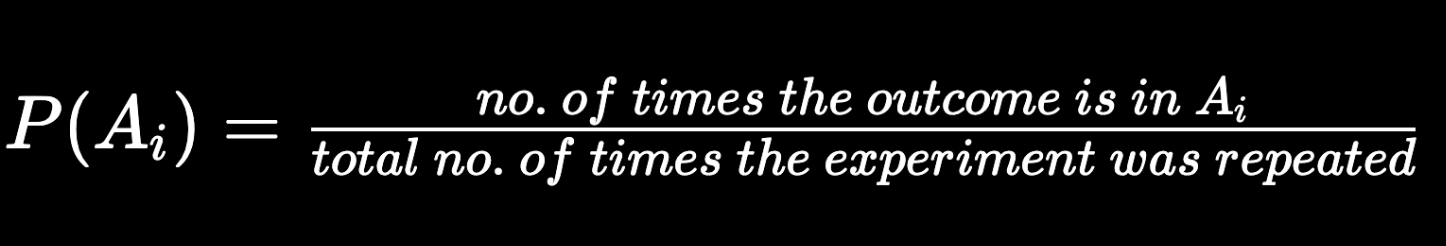
A dataset contains images of beaches (60000), mountains (25000) and forests (15000)
What is the probability that a randomly picked image would be of a forest?
Experiment: Select an image
Number of trials: 100000
Frequency of the event "forest": 15000
P(forest) = \frac{15000}{100000} = 0.15
Examples
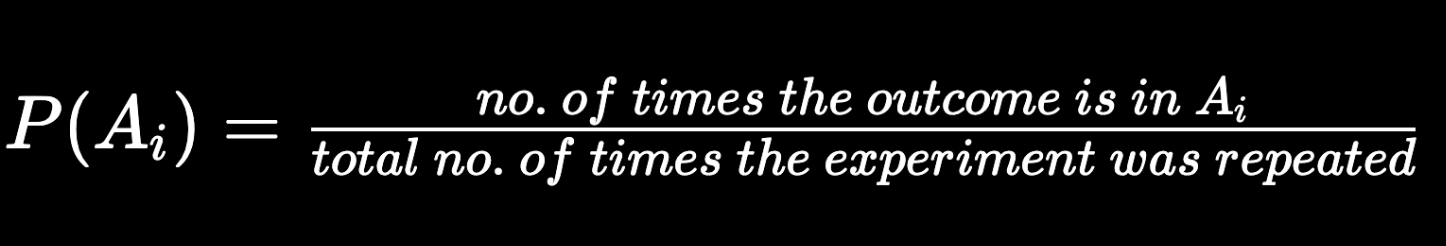
A country tests 20 million randomly selected people and finds that 1 million are infected
What is the probability that a randomly picked person would be infected?
Experiment: Perform a test
Number of trials: 20 million
Frequency of the event "infected": 1 million
P(infected) = \frac{1000000}{20000000} = 0.05
Examples
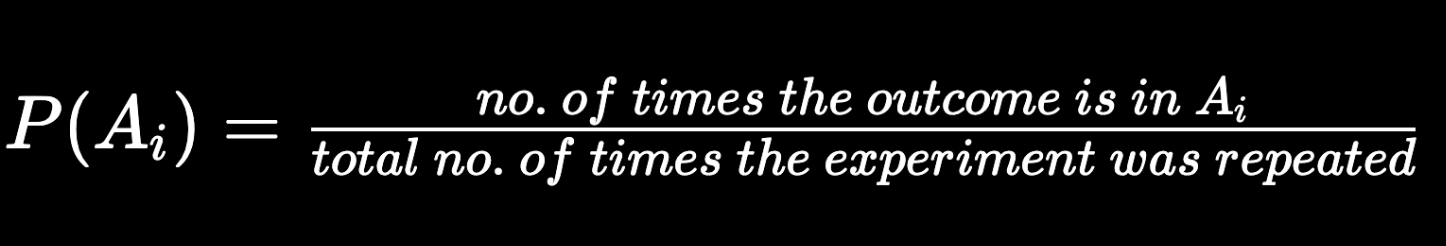
By May-10-2020, India had tested 1673688 samples of which 67176 were found to be positive. Does this mean the probability that a randomly selected person being infected is 0.04
A subtle point: the sample from which the probabilities were estimated should be drawn from the same population on which we are interested in making inferences
No: testing in India was not random but only for people with flu-like symptoms
Flu
\Omega
Designing Probability Functions
(the case of equally likely outcomes)
Equally likely outcomes
P(H) = P(T) = k
\Omega = H \cup T

P(\Omega) = P(H \cup T)
= P(H) + P(T)
\Omega = \{H, T\}
H
T
= 2k
= 1
\therefore P(H) = P(T) = k = \frac{1}{2}
We can now compute the probability of all 4 subsets of
\Omega
\phi, \{H\}, \{T\}, \{H, T\}
Equally likely outcomes
A_i
: event that the out come is i

A_1, A_2, A_3, A_4, A_5, A_6
partition
\Omega
P(A_1) = P(A_2) = P(A_3) = P(A_4) = P(A_5) = P(A_6) = k
P(S) = \sum_{i=1}^6 P(A_i) = 6k = 1
\therefore P(A_i) = \frac{1}{6}
We can now compute the probability of all subsets of
\Omega
\Omega = \{1, 2, 3, 4, 5, 6\}
A_1
A_2
A_3
A_4
A_5
A_6
Equally likely outcomes

We can now compute the probability of all subsets of
\Omega
E
: outcome is even
\Omega = \{1, 2, 3, 4, 5, 6\}
A_1
A_2
A_3
A_4
A_5
A_6
O
: outcome is odd
D
: outcome is divisible by 3
Equally likely outcomes

Can we derive a formula for computing the probability of events of an experiment with n equally likely outcomes?


E
: any event with k outcomes
(the outcomes are of course disjoint)
P(E) = \sum_{i=1}^{k} \frac{1}{n} = \frac{k}{n}
\frac{1}{n}
P(X) = \frac{number~of~outcomes~in~X}{number~of~outcomes~in~\Omega}
Equally likely outcomes

Are the axioms of probability satisfied?


\frac{1}{n}
P(X) = \frac{number~of~outcomes~in~X}{number~of~outcomes~in~\Omega}
P(A_i) \geq 0~?
: ratio of two positive numbers
P(\Omega)=1~?
P(A_1 \cup A_2) = P(A_1)+ P(A_2)~?
: contains all outcomes
A_1
A_2
P(A_1 \cup A_2) = \frac{k_1 + k_2}{n} = \frac{k_1}{n} + \frac{k_2}{n}
= P(A_1) + P(A_2)
Examples
What is the probability of getting a black card?

\frac{1}{n}
P(B) = \frac{26}{52}
P(X) = \frac{number~of~outcomes~in~X}{number~of~outcomes~in~\Omega}
What is the probability of getting 3 aces?
n = {52 \choose 3} = 22100
P(A) = \frac{4}{22100}
Examples
What is the probability of hitting the red circle at the centre?

P(C) = \frac{\pi r^2}{\pi R^2} = (\frac{r}{R})^2
R
: radius of dartboard
r
: radius of red circle
Countably infinite sample space
Examples
Keep tossing the coin till you get the first head
\Omega = \{1,2,3,\dots\}



... ... ...
Suppose
P(n) = \frac{1}{2^n}
(why? we will see later)
Is this a valid probability distribution?
P(n) \geq 0
P(\Omega) = \sum_{i=1}^{\infty}\frac{1}{2^n} = \frac{1}{2}\sum_{i=0}^{\infty} \frac{1}{2^i} = \frac{1}{2}\cdot\frac{1}{1 - \frac{1}{2}} = 1
Examples



... ... ...
What is the probability that \(n\) would be even?
What about the third axiom?
P(outcome~is~even) = P(\{2\} \cup \{4\} \cup \{6\} \cup \dots )
disjoint events
P(outcome~is~even) = P(2) + P(4) + P(6) + \dots
=\frac{1}{2^2} + \frac{1}{2^4} + \frac{1}{2^6} + \dots = \frac{1}{2^2}(1 + \frac{1}{4} + \frac{1}{4^2} + \dots) = \frac{1}{3}
Examples



... ... ...
The third axiom that we had defined earlier was only for finite (countable) events A1,A2,…AnA_1, A_2, \dots A_n
We state its correct version now which accounts for infinite (countable) events A1,A2,…AnA_1, A_2, \dots A_n
Axiom 3 (countable additivity)
= \sum_{i=1}^\infty P(A_i)
P(A_1\cup A_2 \cup \dots )
Summary
Set Theory
Finite, Countably infinite, Uncountably infinite
Intersection, Union, Complement


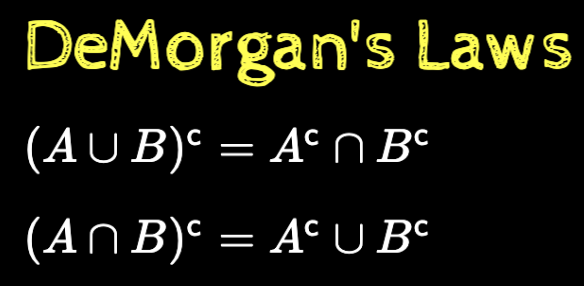

Properties of set operations
Disjoint sets
Axioms of Probability




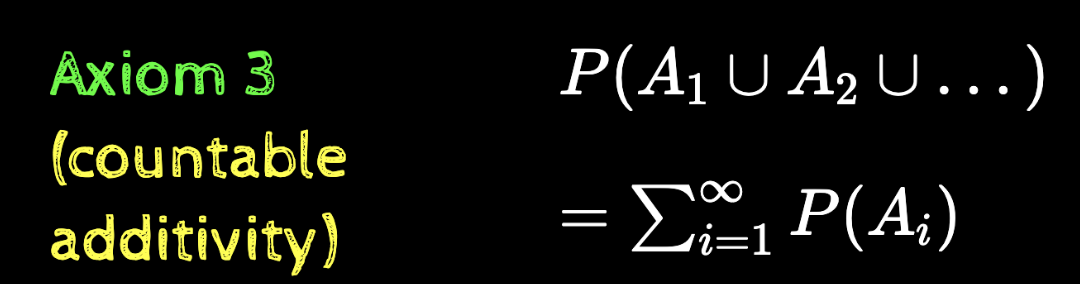
Designing Probability Functions
Goal: Assign a number to each event such that this number reflects the chance of the experiment resulting in that event
Required: The probability function must satisfy the axioms of probability
Probability as long term relative frequency
Equally likely outcomes
Learning Objectives
What is a probability space?
What are the axioms of probability?
What are some simple ways of defining a probability function?
CS6015: Lecture 28
By Mitesh Khapra
CS6015: Lecture 28
Lecture 28: Probability Space, Axioms of Probability, Designing Probability Functions
- 3,369



