GloVe
Papers We Love San Diego
July 5th, 2018
Presented by Michael Jalkio
Global Vectors for Word Representation
Today
- What is NLP?
- Early influence: Vector Space Models
- What & why of word embeddings
- Word2vec
- GloVe
Natural Language Processing
- Sentence parsing
- Machine translation
- Natural language generation
- Question answering
- Sentiment analysis
- ...and so much more!
Representing Language
Vector Space Models
(Information Retrieval)
The Setup
We start with a corpus of documents.
$$ C = \{ d_1, d_2, d_3 \} $$
We examine the words in the corpus to build a vocabulary.
$$ V = \{ w_1, w_2, w_3, w_4, w_5 \} $$
Documents are represented as vectors of term weights.
$$d_1 = (w_{1,1}, w_{2,1}, w_{3,1}, w_{4,1}, w_{5,1})$$
$$d_2 = (w_{1,2}, w_{2,2}, w_{3,2}, w_{4,2}, w_{5,2})$$
$$d_3 = (w_{1,3}, w_{2,3}, w_{3,3}, w_{4,3}, w_{5,3})$$
Making a Query
A query is similarly represented by a term weight vector.
$$ q = (w_{1,q}, w_{2,q}, w_{3,q}, w_{4,q}, w_{5,q})$$
Cosine similarity is used to compare the query to documents.
$$\cos(d_i, q) = \frac{d_i^T q}{\| d_i \| \| q \|}$$
Because vectors are nonnegative:
$$\cos(d_i, q) \in [0,1]$$
Deciding on Weights
A first approach is a bag of words.
- The dog runs.
- The horse runs.
- The dog eats.
- The dog eats dog.
Vectors contain counts of the terms the documents contain.
$$d_1 = [1, 1, 1, 0, 0]$$
$$d_2 = [1, 0, 1, 1, 0]$$
$$d_3 = [1, 1, 0, 0, 1]$$
$$d_4 = [1, 2, 0, 0, 1]$$
Better Weights...
BoW overemphasizes common words.
An improvement is term frequency-inverse document frequency.
$$w_{t,d} = tf_{t,d} \cdot \log{\frac{|D|}{| \{ d \in D : t \in d \} |}}$$
From the example before we get:
$$idf(\text{the}, D) = \log{\frac{4}{4}} = 0$$
$$idf(\text{dog}, D) = \log{\frac{4}{3}} \approx 0.125$$
$$idf(\text{runs/eats}, D) = \log{\frac{4}{2}} \approx 0.301$$
$$idf(\text{horse}, D) = \log{\frac{4}{1}} \approx 0.602$$
From Documents
to Words
Word Representation
Source: Andrew Ng / deeplearning.ai Sequence Models course
Man
(5391)
Woman
(9853)
King
(4914)
Queen
(7157)
Apple
(456)
Orange
(6257)
One-Hot Encodings
Featurized Representation: Word Embedding
Source: Andrew Ng / deeplearning.ai Sequence Models course
| Man | Woman | King | Queen | Apple | Orange | |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Food | 0.04 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
Why Do We Care?
Source: Andrew Ng / deeplearning.ai Sequence Models course
One potential application is named entity recognition.
If the training set contains:
- Sally Johnson is an orange farmer.
And the test set contains:
- Robert Lin is a durian cultivator.
You can use word embeddings to figure out that these sentences have very similar structures.
Nearest Neighbors are Synonyms
Nearest neighbors to frog:
- Frogs
- Toad
- Litoria
- Leptodactylidae
- Rana
- Lizard
- Eleutherodactylus

Source: https://nlp.stanford.edu/projects/glove
More Generally...
You can pre-train word embeddings in an unsupervised manner on a large corpus of text data.
Or even use someone else's pre-trained model!
You can then use embeddings to squeeze out more information from a smaller training set for your task.
Generally, this technique is called transfer learning.
Analogies
| Man | Woman | King | Queen | Apple | Orange | |
|---|---|---|---|---|---|---|
| Gender | -1 | 1 | -0.95 | 0.97 | 0.00 | 0.01 |
| Royal | 0.01 | 0.02 | 0.93 | 0.95 | -0.01 | 0.00 |
| Food | 0.04 | 0.01 | 0.02 | 0.01 | 0.95 | 0.97 |
Woman is to man as queen is to _ ?
Analogies
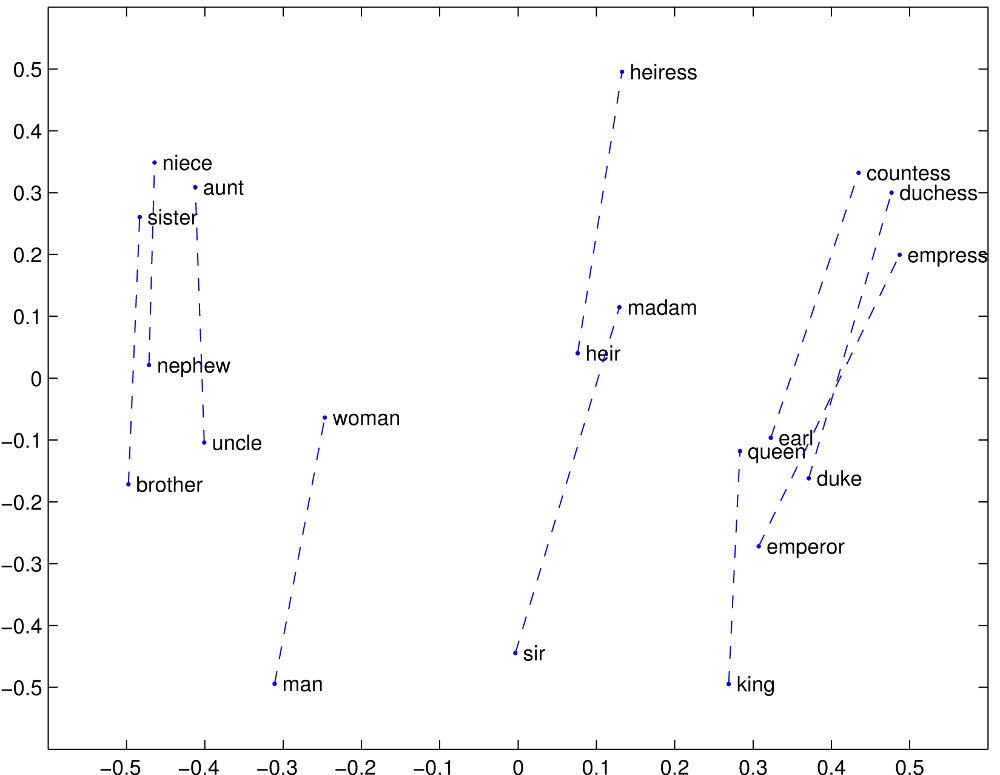
Source: https://nlp.stanford.edu/projects/glove
Analogies
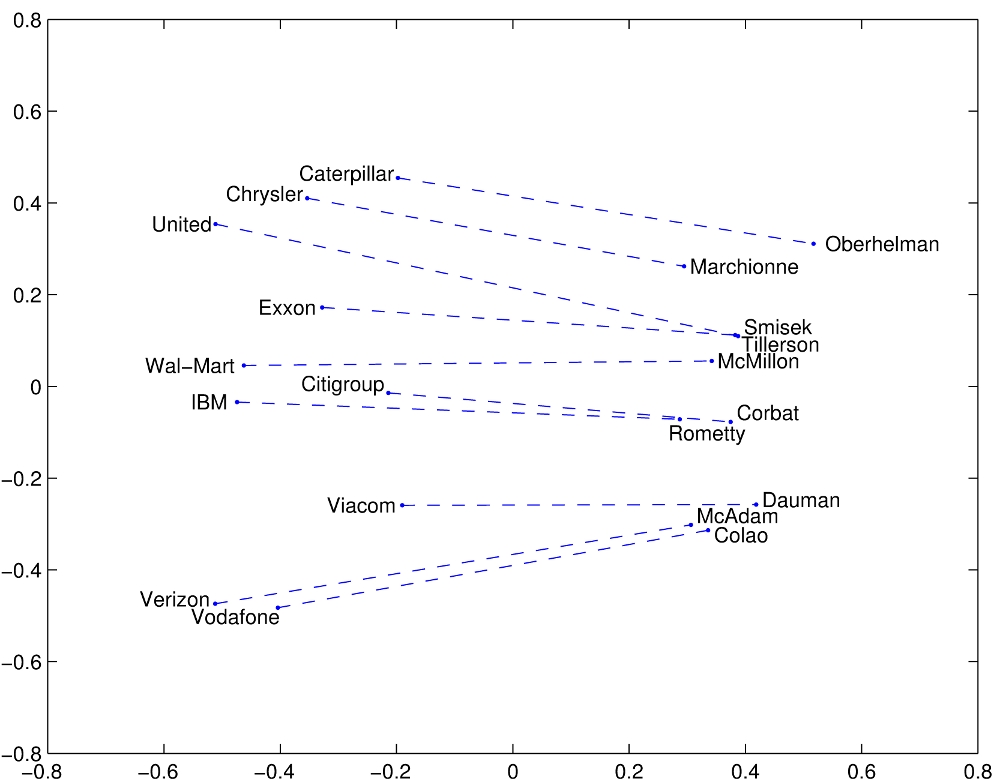
Source: https://nlp.stanford.edu/projects/glove
Analogies
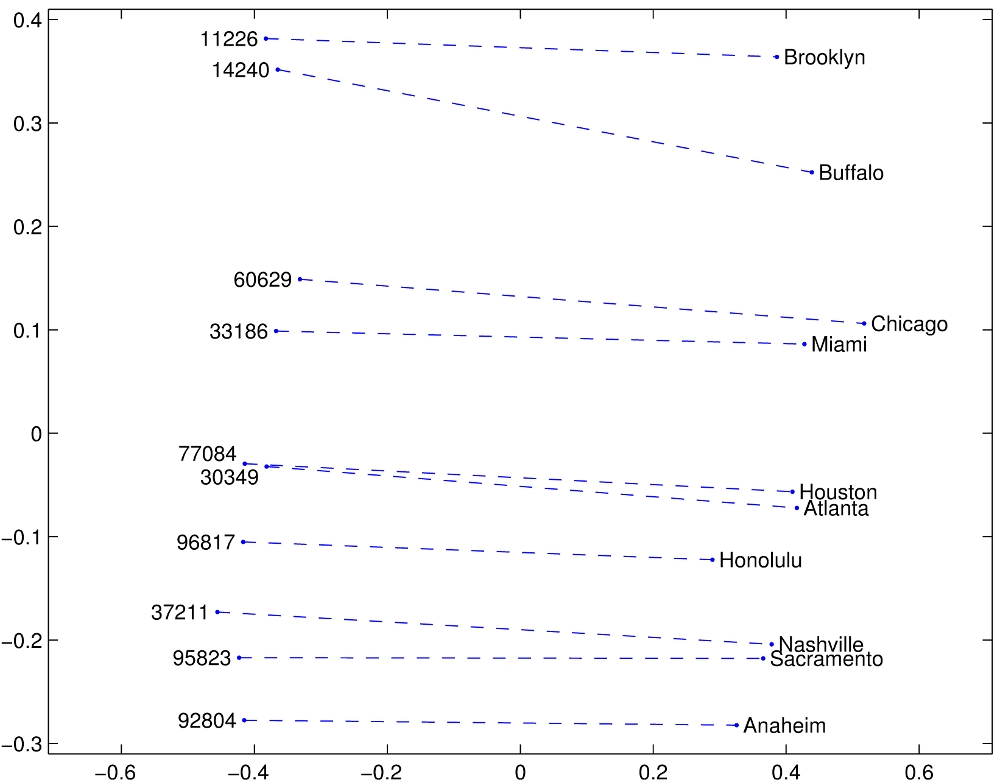
Source: https://nlp.stanford.edu/projects/glove
Analogies
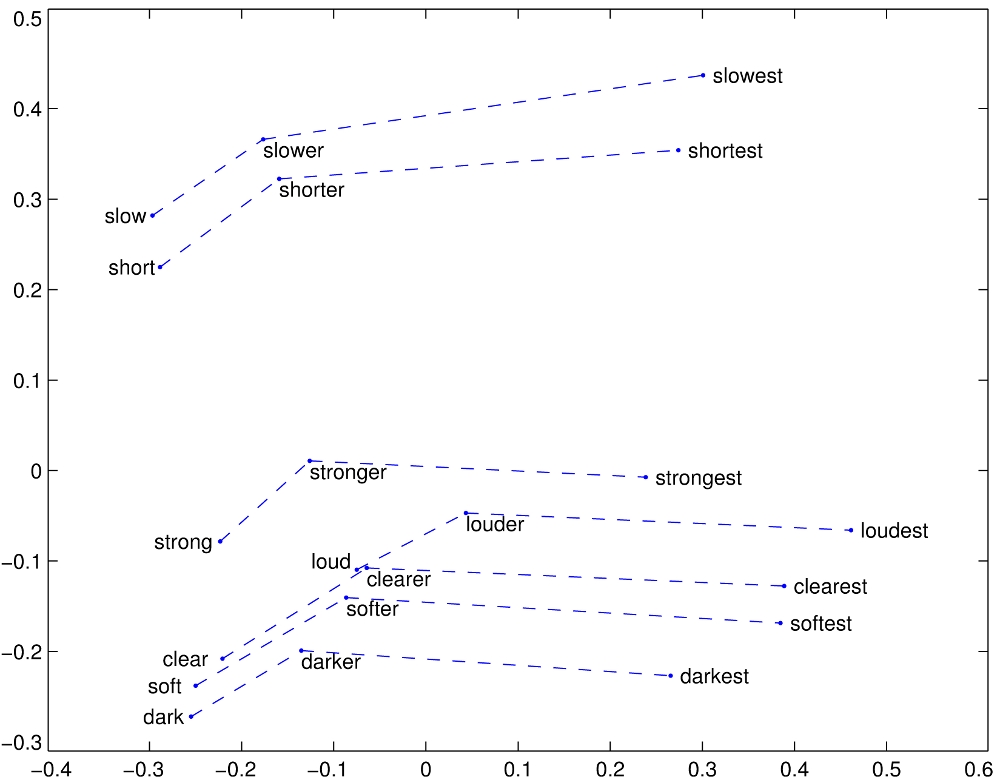
Source: https://nlp.stanford.edu/projects/glove
Word2vec
Continuous Bag of Words
Task: given a context, predict the word that fits.
The quick brown fox jumps over the lazy dog.
The quick ___ fox jumps
quick brown ___ jumps over
brown fox ___ over the
Skip-Gram
Task: given a word, predict the context.
The quick brown fox jumps over the lazy dog.
brown => {The, quick, fox, jump}
fox => {quick, brown, jumps, over}
jumps => {brown, fox, over, the}
Architecture
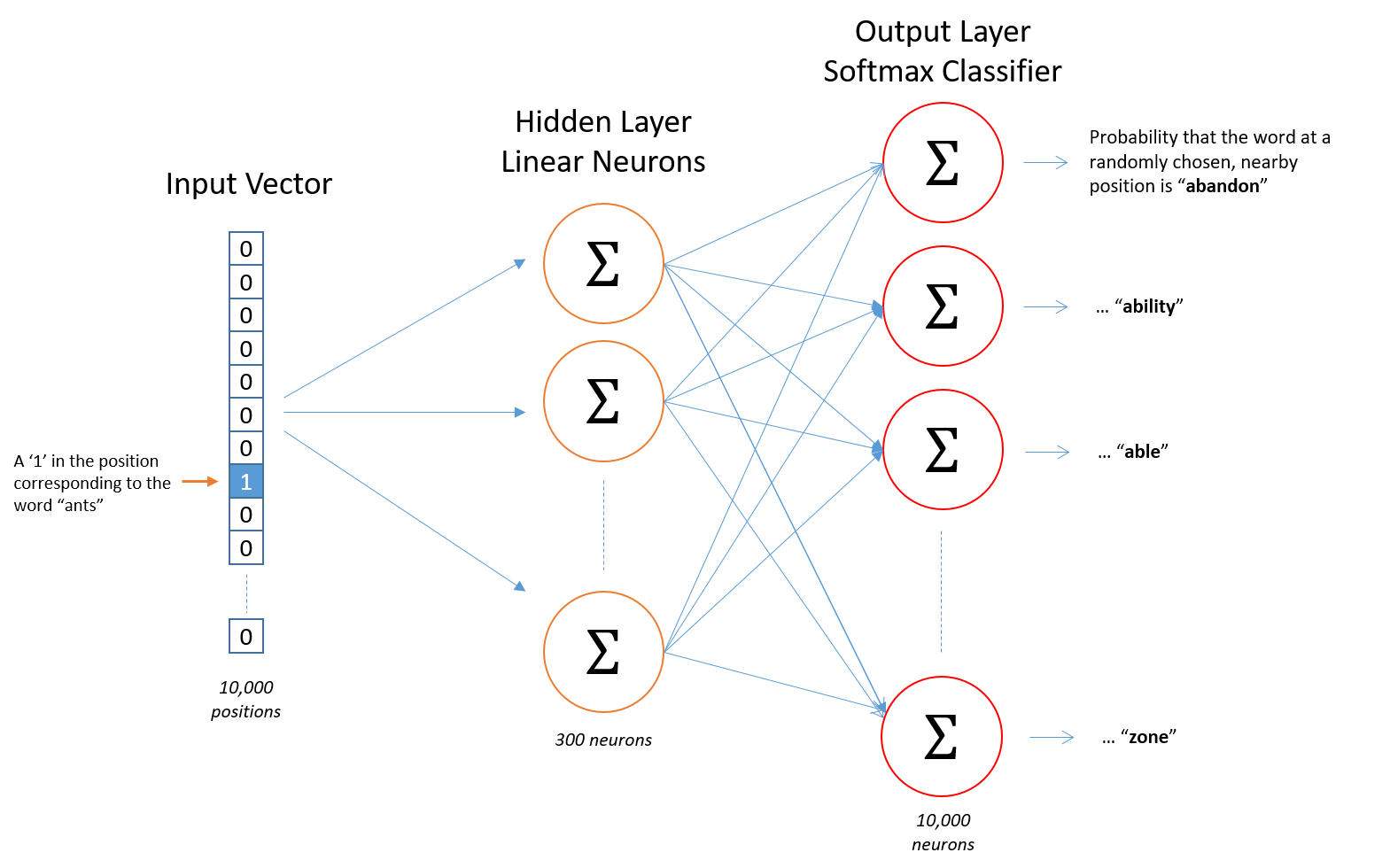
Source: McCormick, C. (2016, April 19). Word2Vec Tutorial - The Skip-Gram Model. Retrieved from http://www.mccormickml.com
Word Embeddings
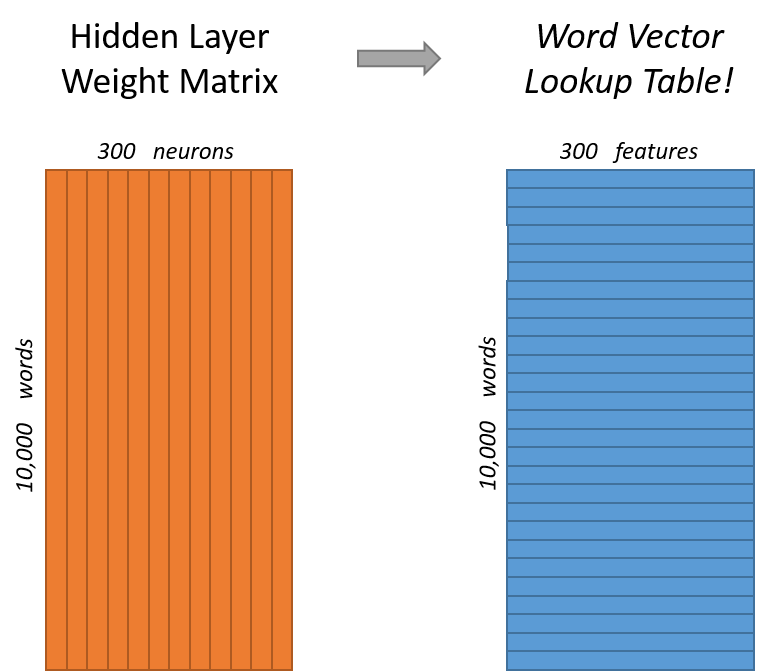
Source: McCormick, C. (2016, April 19). Word2Vec Tutorial - The Skip-Gram Model. Retrieved from http://www.mccormickml.com
GloVe
Goals
- More computationally efficient model
- Clearer training objective + motivation
Definitions
Number of times word j occurs in context of word i
Number of times any word appears in the context of word i
Probability that word j appear in the context of word i
Co-occurence Probabilities
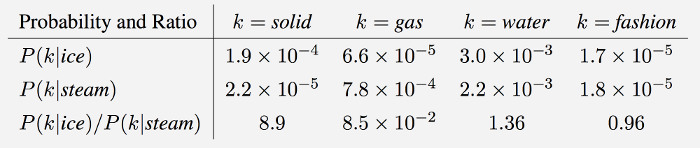
The ratios are better at surfacing relevant words.
- For words k related to i but not j, \( P_{ik} / P_{jk} \) will be large.
- For words k related to j but not i, \( P_{ik} / P_{jk} \) will be small.
- For words k related to both i and j (or to neither), \( P_{ik} / P_{jk} \) will be close to 1.
Designing a Model
(the GloVe algorithm)
Calculated directly from our corpus
Word vectors
Context word vector
A function that will tie everything together
We want relationships between words to be embedded in a vector space.
Encodes whether words are related
Encodes a relationship
Scalar
Vectors
Want to work in simple, linear structures.
Want to work in simple, linear structures.
A word and a context word should be an arbitrary distinction.
$$w \leftrightarrow \tilde{w}$$
For this to be possible, our
co-occurrence matrix needs to be symmetric.
$$X \leftrightarrow X^T$$
If \( F \) obeys this, it is a homomorphism between the groups \( (\mathbb{R}, +) \) and \( (\mathbb{R}_{>0}, \times) \)
$$F: \mathbb{R} \to \mathbb{R}_{>0}$$
$$\forall a,b \in \mathbb{R}, F(a+b) = F(a) \times F(b)$$
What about \( \log(0) \)?
Wrapping Up Loose Ends
Very common solution to \(log(0)\) is to add 1:
$$\log(X_i) \to \log(1 + X_i)$$
But we have another issue. We treat all co-occurrences equally. Most are zero, and the ones that exist are often huge.
Let's fix two problems at once with a weighting function.
Wrapping Up Loose Ends
Our weighting function should have:
- \( f(0) = 0 \) to solve the \( \log \) issue.
- \( f(x) \) be non-decreasing so that rare co-occurrences are not overweighted
- \( f(x) \) should be small for large \( x \) so that frequency co-occurrences are not overweighted
The Final Model
We cast the problem as a weighted least squares regression model, which is a standard machine learning problem.
The word vectors (along with bias, which we can discard) that are returned when we minimize this function, are our embeddings!
Evaluation
Complexity
- Operates on nonzero elements of \( X \), so at worst \( O(|V|^2) \)
- Find that in practice, it's \( O(|C|^{0.8}) \), better than the \( O(|C|) \) of Word2Vec
Experiments
- Evaluate on word analogy, word similarity, and NER tasks
- GloVe performs well compared to "similarly-sized" models
My Thoughts
- I see GloVe as a protest against "deep learning" methods
- Simple and understandable is sometimes worth it
Questions?
GloVe (PWL San Diego 2018/07/05)
By mjalkio
GloVe (PWL San Diego 2018/07/05)
- 1,057



