Michael Recachinas
Software Engineer by day, Puppy dad by night


Step 1: Lexer
Step 2: Parser
Step 3: Type Checker
Step 4: Interpreter
Step 5: ???
Step 6: Profit!
If you don’t know how compilers work, then you don’t know how computers work. If you’re not 100% sure whether you know how compilers work, then you don’t know how they work.

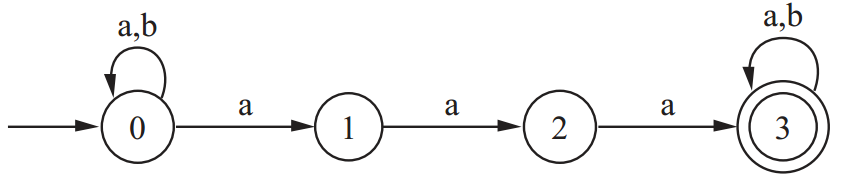
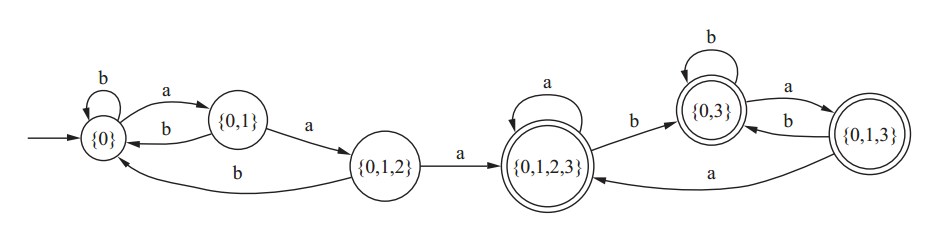
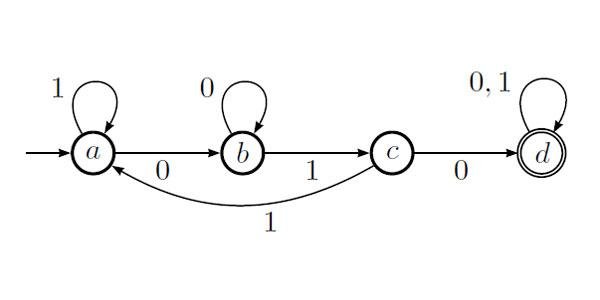
(1*0+11*)+(0(0|1)*) >> email_string = "mike@gmail.com, yadu@yahoo.org, chris@hotmail.edu"# Say I want to find the domains (i.e., domain.com) in test_string >> import re >> re.findall( r'(?<=@)[A-z]+.[com|net|org|edu]*', email_string )['gmail.com', 'yahoo.org', 'hotmail.edu']
$ cat employees.txt
Name Phone Number Undergraduate School
Michael R 202 123 4567 Virginia Tech
Yadu R 703 321 4567 University of Virginia
Chris S 301 987 4567 CalTech
$ grep -o '^[A-z ][A-z ]*[0-9]\{3\} ' employees.txt | sed 's/[A-z ]*//g' | sort -u
202
301
703A lexer is made up of regexes that take
let x = 5 in {
print (x + 1)
}; LET
IDENTIFIER x
EQ
INTEGER 5
IN
LBRACE
IDENTIFIER print
LPAREN
IDENTIFIER x
PLUS
INTEGER 1
RPAREN
RBRACE
SEMICOLON{
open Parse
}
let blank = [' ' '\012' '\r' '\t' '\n']
rule initial = parse
"/*" { let _ = comment lexbuf in initial lexbuf }
| "(*" { let _ = comment2 lexbuf in initial lexbuf }
| "//" { endline lexbuf }
| blank { initial lexbuf }
| '+' { PLUS }
| '-' { MINUS }
| '*' { TIMES }
| "true" { TRUE }
| "false" { FALSE }
| "="
| "==" { EQ_TOK }
| "<=" { LE_TOK }
| '!' { NOT }
| "&&"
| "/\\" { AND }
| "||"
| "\\/" { OR }
| "skip" { SKIP }
| ":=" { SET }
| ';' { SEMICOLON }
| "if" { IF }
| "then" { THEN }
| "else" { ELSE }
| "while" { WHILE }
| "do" { DO }
| "let" { LET }
| "in" { IN }
| "print" { PRINT }
| '(' { LPAREN }
| ')' { RPAREN }
| '{' { LBRACE }
| '}' { RBRACE }
| ("0x")?['0'-'9']+ {
let str = Lexing.lexeme lexbuf in
INT((int_of_string str)) }
| ['A'-'Z''a'-'z''_']['0'-'9''A'-'Z''a'-'z''_']* {
let str = Lexing.lexeme lexbuf in
IDENTIFIER(str)
}
| '.'
| eof { EOF }
| _ {
Printf.printf "invalid character '%s'\n" (Lexing.lexeme lexbuf) ;
(* this is not the kind of error handling you want in real life *)
exit 1 }
and comment = parse
"*/" { () }
| '\n' { comment lexbuf }
| eof { Printf.printf "unterminated /* comment\n" ; exit 1 }
| _ { comment lexbuf }
and comment2 = parse
"*)" { () }
| '\n' { comment2 lexbuf }
| "(*" { (* ML-style comments can be nested *)
let _ = comment2 lexbuf in comment2 lexbuf }
| eof { Printf.printf "unterminated (* comment\n" ; exit 1 }
| _ { comment2 lexbuf }
and endline = parse
'\n' { initial lexbuf}
| _ { endline lexbuf}
| eof { EOF }
balanced( "(())" ) #=> should return true
balanced( "))((" ) #=> should return false
balanced( "())" ) #=> should return false
balanced( "(()" ) #=> should return false
balanced( "(()()(())((((((()))))))())" ) #=> should return true
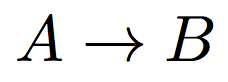
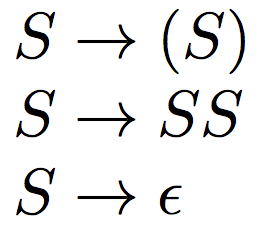

Programming languages usually follow a context free grammar*
function hello(x) { // <-- matched parentheses, matched braces
return 3;
} // <--
Cheryl gave Jane her notes.
James while John had had had had had had had had had had had a better effect on the teacher.
Buffalo buffalo buffalo buffalo buffalo buffalo buffalo buffalo.

Colorless green ideas sleep furiously
Noam Chomsky

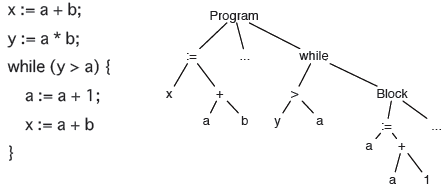
%start expressions
%%
expressions
: e EOF
{return $1;}
;
e
: e '+' e
{$$ = $1+$3;}
| e '-' e
{$$ = $1-$3;}
| e '*' e
{$$ = $1*$3;}
| e '/' e
{$$ = $1/$3;}
| '(' e ')'
{$$ = $2;}
| INTEGER
{$$ = Number(yytext);}
;
%{
open Imp
let error msg = failwith msg
%}
%token <string> IDENTIFIER
%token <int> INT
%token PLUS
%token MINUS
%token TIMES
%token TRUE
%token FALSE
%token EQ_TOK
%token LE_TOK
%token NOT
%token AND
%token OR
%token SKIP
%token SET
%token SEMICOLON
%token IF
%token THEN
%token ELSE
%token WHILE
%token DO
%token LET
%token IN
%token PRINT
%token LPAREN
%token RPAREN
%token LBRACE
%token RBRACE
%token EOF
%start com
%type <Imp.com> com
%left AND
%left OR
%left PLUS MINUS
%left TIMES
%left LE_TOK EQ_TOK
%nonassoc NOT
%%
aexp : INT { Const($1) }
| IDENTIFIER { Var($1) }
| aexp PLUS aexp { Add($1,$3) }
| aexp MINUS aexp { Sub($1,$3) }
| aexp TIMES aexp { Mul($1,$3) }
| LPAREN aexp RPAREN { $2 }
;
bexp : TRUE { True }
| FALSE { False }
| aexp EQ_TOK aexp { EQ($1,$3) }
| aexp LE_TOK aexp { LE($1,$3) }
| NOT bexp { Not($2) }
| bexp AND bexp { And($1,$3) }
| bexp OR bexp { Or($1,$3) }
;
com : SKIP { Skip }
| IDENTIFIER SET aexp { Set($1,$3) }
| com SEMICOLON com { Seq($1,$3) }
| IF bexp THEN com ELSE com { If($2,$4,$6) }
| WHILE bexp DO com { While($2,$4) }
| LET IDENTIFIER EQ_TOK aexp IN com { Let($2,$4,$6) }
| PRINT aexp { Print($2) }
| LBRACE com RBRACE { $2 }
;
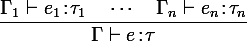
"If expression e i has type τ i in environment Γ i for all i = 1.. n, then the expression e will have an environment Γ and type τ.
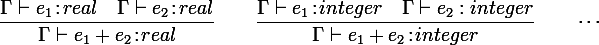
"If expression e 1 has type real in environment Γ and e 2 has type real in environment Γ, then the expression e 1 + e 2 will have an environment Γ and type real.
"If expression e 1 has type integer in environment Γ and e 2 has type integer in environment Γ, then the expression e 1 + e 2 will have an environment Γ and type integer.
int x = 0;
int y = 5;
{
printf("1. x: %d, y: %d\n", x, y);
{
int x = 5;
printf("2. x: %d, y: %d\n", x, y);
{
int y = 10;
printf("3. x: %d, y: %d\n", x, y);
x = 100;
}
printf("4. x: %d, y: %d\n", x, y);
}
printf("5. x: %d, y: %d\n", x, y);
}
$ gcc -o scoping scoping.c --std=c89
$ ./scoping
1. x: 0, y: 5
2. x: 5, y: 5
3. x: 5, y: 10
4. x: 100, y: 5
5. x: 0, y: 5
let x = 1 in
let y = x + 1 in
let z = y + 3 in
print_int z
;;
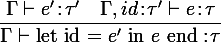
If expression e' has type τ' and expression e has type τ in the environment Γ with the new variable "id" having type τ', then the let expression will have type τ.
addi $r1, $r2, $r3 # addi is add immediate; $r1 = $r2 + $r3
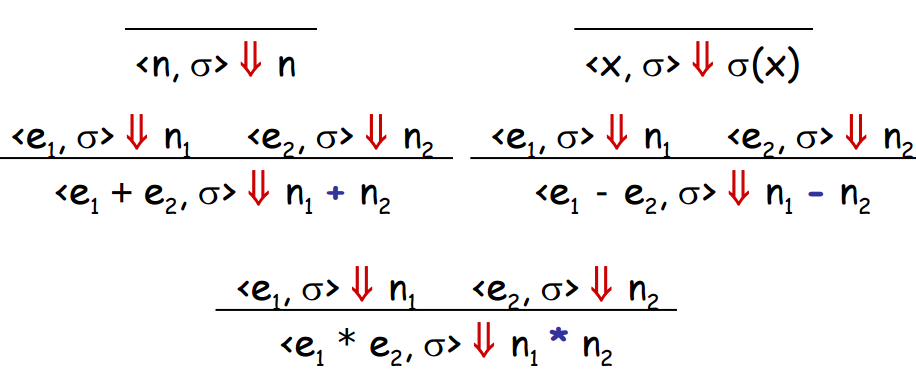
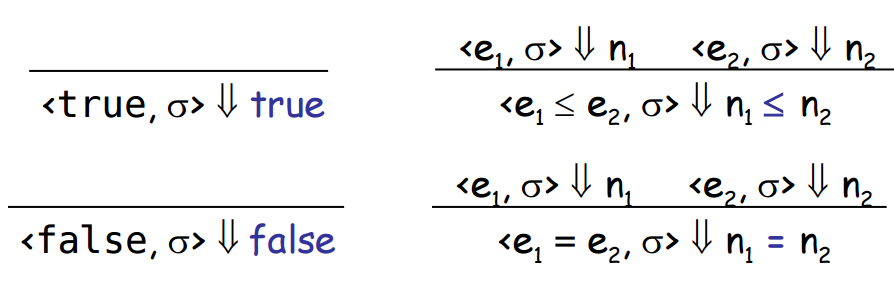
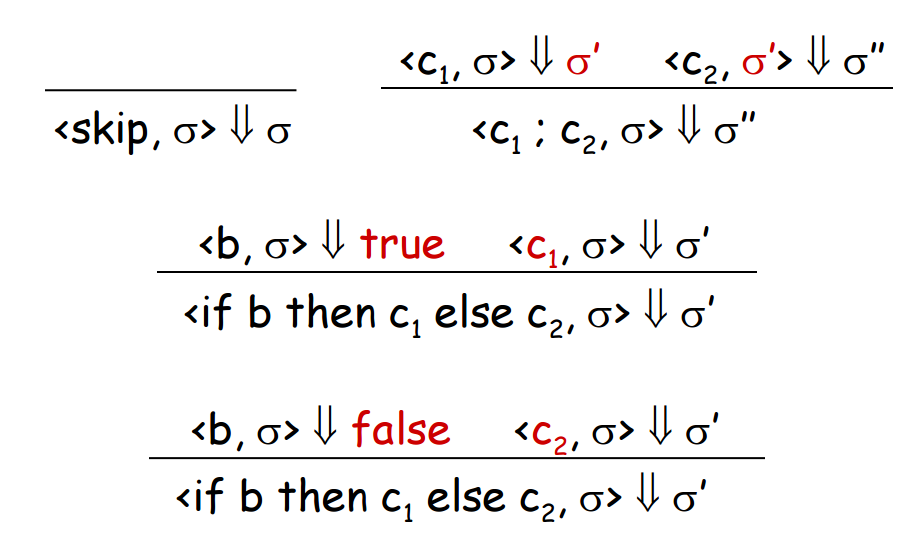
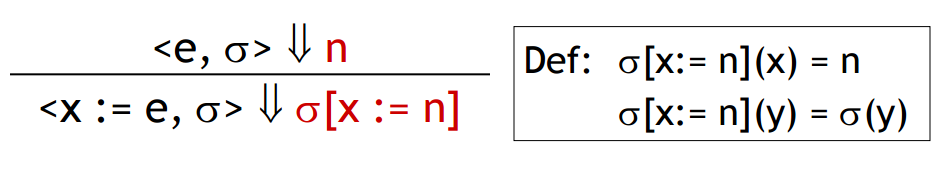

(*
* Our operational semantics has a notion of 'state' (sigma). The type
* 'state' is a side-effect-ful mapping from 'loc' to 'n'.
*
* See http://caml.inria.fr/pub/docs/manual-ocaml/libref/Hashtbl.html
*)
type state = (loc, n) Hashtbl.t
let initial_state () : state = Hashtbl.create 255
(* Given a state sigma, return the current value associated with
* 'variable'. For our purposes all uninitialized variables start at 0. *)
let lookup (sigma:state) (variable:loc) : n =
try
Hashtbl.find sigma variable
with Not_found -> 0
(* Evaluates an aexp given the state 'sigma'. *)
let rec eval_aexp (a:aexp) (sigma:state) : n = match a with
| Const(n) -> n
| Var(loc) -> lookup sigma loc
| Add(a0,a1) ->
let n0 = eval_aexp a0 sigma in
let n1 = eval_aexp a1 sigma in
n0 + n1
| Sub(a0,a1) ->
let n0 = eval_aexp a0 sigma in
let n1 = eval_aexp a1 sigma in
n0 - n1
| Mul(a0,a1) ->
let n0 = eval_aexp a0 sigma in
let n1 = eval_aexp a1 sigma in
n0 * n1
(* Evaluates a bexp given the state 'sigma'. *)
let rec eval_bexp (b:bexp) (sigma:state) : t = match b with
| True -> true
| False -> false
| EQ(a0,a1) ->
let n0 = eval_aexp a0 sigma in
let n1 = eval_aexp a1 sigma in
n0 = n1
| LE(a0,a1) ->
let n0 = eval_aexp a0 sigma in
let n1 = eval_aexp a1 sigma in
n0 <= n1
| Not(b) ->
not (eval_bexp b sigma)
| And(b0,b1) ->
let n0 = eval_bexp b0 sigma in
let n1 = eval_bexp b1 sigma in
n0 && n1
| Or(b0,b1) ->
let n0 = eval_bexp b0 sigma in
let n1 = eval_bexp b1 sigma in
n0 || n1
(* Evaluates a com given the state 'sigma'. *)
let rec eval_com (c:com) (sigma:state) : state = match c with
| Skip -> sigma
| Set(l,a) ->
let n = eval_aexp a sigma in
Hashtbl.add sigma l n;
sigma
| Seq(c0,c1) ->
let new_sigma = eval_com c0 sigma in
eval_com c1 new_sigma
| If(b,c0,c1) ->
if eval_bexp b sigma then
eval_com c0 sigma
else
eval_com c1 sigma
| While(b,c) ->
if not (eval_bexp b sigma) then
sigma
else begin
let new_sigma = eval_com c sigma in
let new_c = While(b,c) in
eval_com new_c new_sigma
end
| Let(l,a,c) ->
let original_n = lookup sigma l in
let n = eval_aexp a sigma in
Hashtbl.add sigma l n;
let new_sigma = eval_com c sigma in
Hashtbl.replace new_sigma l original_n;
new_sigma
| Print(a) ->
Printf.printf "%d" (eval_aexp a sigma);
sigma
let x = 5 in {
print x + 1
} mov %eax, 5 ; read this as "move 5 into %eax"
inc %eax ; the same as "add %eax, 1"
push %eax ; pushing %eax to the stack so it will be available by the callee "_print"
call _print ; call the internal assembly method to print the contents of %eax // original language
let x = 5 in {
if x = 5 then print "Hello" else print "Bye!"
let y = 6 in {
print x + 1
}
}
# Intermediate Level 1
x := 5
if x = 5 goto L1
print "Bye"
goto L2
L1: print "Hello"
L2: y := 6
x := x + 1
print x
# Intermediate Level 2 - optimized version
x := 5
print "Hello"
x := x + 1
print x
; Pseudo-Assembly
mov %eax, 5
push "Hello"
call _print
inc %eax
push %eax
call _print
# Intermediate Level 2 - optimized version
x := 5
print "Hello"
x := x + 1
print x
# Intermediate Level 3 - further optimized version
print "Hello"
print 6
; Pseudo-Assembly from IL3
push "Hello"
call _print
push 6
call _print





By Michael Recachinas