Dataset Sensitive Autotuning of Multi-Versioned Code based on Monotonic Properties
Autotuning in Futhark
Art by Robert Schenck
Philip Munksgaard, Svend Lund Breddam, Troels Henriksen, Fabian Cristian Gieseke & Cosmin Oancea
A general method for finding the near-optimal* tuning parameters for multi-versioned code
* Subject to some assumptions
A general method for finding the near-optimal* tuning parameters for multi-versioned code
- A way of choosing at run-time between multiple semantically identical but differently optimized versions of code
- Generalizes to all programs that are structured in a similar way
- Is implemented as part of the Futhark project
- Functional languages are ideal for experimenting with generating different code versions
This talk
- Motivation and running example
- Autotuning
- Results
- Related work
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
Two levels of parallelism
- Outer parallelism
- Degree m
- Inner parallelism
- Degree n
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
- There could be any number of levels of parallelism in the code
- Hardware has limited number of levels of parallelism
- How do we map code to hardware?
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
Ways to parallelize
- Parallelize outer, sequentialize inner
- Parallelize inner, sequentialize outer
- There are more ways
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
Tall matrix?
\(m\) threads, sequential inner code
n = 5
m = 100
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
\(n\) threads,
sequential outer code
n = 100
m = 5
Wide matrix?
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
So which version to use?
Inner or outer?
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
We don't know at compile-time!
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
map2 (\(row: [n]i32) (i: i32) ->
loop (row: [n]i32) for _ in 0..<64 do
let row' = map (+ i) row
in scan (+) 0 row'
)
xss (0..<m)
An example
Instead, let's generate multiple versions, and choose at compile-time
Henriksen, Troels, et al. "Incremental flattening for nested data parallelism." Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming. 2019.
Incremental flattening!
m \geq t
Parallelize outer
Parallelize inner
true
false
An example
Incremental flattening!
m \geq t
Parallelize outer
Parallelize inner
true
false
An example
Incremental flattening!
- Generate multiple different versions of code
- Right-leaning tree
- \(p\) was degree of parallelism of left child, but can be any scalar known at run-time
- \(t\) is "user-defined" threshold
p_1 \geq t_1
true
false
p_2 \geq t_2
Version 2
true
false
Version 3
Version 1
An example
p_1 \geq t_1
true
false
p_2 \geq t_2
Version 2
true
false
Version 3
Version 1
But how do we determine set of \(t\) that gives us best performance, for all datasets?
- Really an optimization problem
- Minimize number of test-runs
Autotuning
Assumptions
- Right-leaning tree, but generalizes to forests
- A single unknown per threshold/branch
- Monotonicity requirement
- Compiler instrumentation
- Representative datasets
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Size-invariance
- Size-invariant: During the execution of a certain dataset, \(p_i\) is constant
\(p_1\) can be size-variant and \(p_2\) can be size-invariant on a certain dataset
Analysis is done per-threshold
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Size-invariance
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
n = 100
m = 5
Input:
\(p_1\) is height of matrix (\(m\))
So the size is invariant
5
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Size-invariance
What if there's a loop?
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
What if there's a loop?
loop:
n = 100
m = 5
Input:
n = 100
m = 5
n = 100
m = 5
n = 100
m = 5
\{5, 5, 5, 5\}
Still invariant
Size-invariance
Size-invariant tuning
For each dataset, a single code version is best
Therefore, to tune a program on a single dataset, run each code version once and pick thresholds such that the fastest version is executed
To tune a program on multiple datasets, tune individually and combine thresholds, somehow
Autotuning a single dataset
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
How do we make sure each version is run exactly once?
Program and dataset is given as is, we only control thresholds
Bottom-up traversal of the tuning tree
Autotuning a single dataset
Setting all thresholds to \(\infty\) forces the bottom-most version to run
p_1 \geq
p_2 \geq
v_1
v_2
v_3
t_1
t_2
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
Setting all thresholds to \(\infty\) forces the bottom-most version to run
\infty
\infty
This allows us to record the run-time of \(v_3\)
With a bit of compiler instrumentation, we can also get information about what \(p_1\) and \(p_2\) was when they were compared against the thresholds
This allows us to pick \(v_2\) next
p_1 = 10
p_2 = 100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
Setting \(t_2 = 100\) (or any value below that) will force execution of \(v_2\)
100
Now, we can set the threshold \(t_2\) optimally for the bottom-most branch
Any value for \(t_2\) larger than 100 will select \(v_3\). Any value lower than 100 will select \(v_2\)
Thus, the optimal choice is a range:
If \(v_2\) is preferable, \(0 \leq t_2 \leq 100\)
Autotuning a single dataset
p_1 \geq
p_2 \geq
v_1
v_2
v_3
\infty
p_1 = 10
p_2 = 100
100
To continue tuning, collapse bottom nodes into one and repeat
Autotuning a single dataset
p_1 \geq
v_1
\infty
p_1 = 10
To continue tuning, collapse bottom nodes into one and repeat
v_2'
We already know the best run-time for \(v_2'\), so we can jump straight to running \(v_1\)
Autotuning multiple datasets
For each dataset, we have found an optimal range for each threshold
We need to combine the tuning results from each dataset
Example:
Dataset 1: \(0 \leq t_2 \leq 100\) is optimal
Dataset 2 : \(50 < t_2 \leq \infty\) is optimal
Intersecting those ranges, \(50 < t_2 \leq 100\) is optimal for both datasets!
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Autotuning multiple datasets
But is there always a valid intersection?
Example:
Dataset 1: \(0 \leq t_2 \leq 100\)
Dataset 2: \(500 < t_2 \leq \infty\)
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Monotonicity assumption
p_1 \geq t_1
v_1
v_2
\(p_1\) represents parallelism of \(v_1\)
If \(v_1\) is faster than \(v_2\) for a given value of \(p_1\), it should also be faster for larger values
\(p_1\) could represent something else, but we assume that the same property holds
Monotonicity assumption
Besides, if no range intersection exists, no choice of \(t_2\) will choose the best code version for all datasets
p_1 \geq t_1
v_1
v_2
Size-invariant tuning
This method allows us to optimally tune size-invariant programs using exactly \(n \times d\) runs
\(n\): number of code versions
\(d\): number of datasets
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
loop:
But the size can change
Size-variance
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
loop:
But the size can change
n = 100
m = 5
Input:
n = 5
m = 100
n = 50
m = 50
\{5, 50, 100\}
This program is size-variant!
Size-variance
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
loop:
\{5, 5, 5, 5\}
Size-variance
When the program is size-invariant, there is always a single best version of the code for each dataset
Always prefer \(v_1\) for this dataset
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
loop:
\{5, 50, 100\}
Size-variance
When the program is size-variant, there is not always a single best version of the code for each dataset
When \(p_1\) is \(5\) or \(50\), prefer \(v_1\) otherwise prefer \(v_2\)
Size-variant tuning
loop:
\{5, 50, 100\}
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
It's no longer enough to run each code version once for each dataset
Each dataset does not necessarily have a single best code version
n = 100
m = 5
Input:
n = 5
m = 100
n = 50
m = 50
Size-variant tuning
loop:
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Each dataset does not necessarily have a single best code version
Best for \(p_2 = 50, 100\)
Best for \(p_2 = 5\)
Result is still a range, and combining results is still the same, but how do we efficiently find the best range for each dataset?
Size-variant tuning
loop:
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Best for \(p_2 = 50, 100\)
Best for \(p_2 = 5\)
Only values in \(\{0, 5, 50, 100, \infty\}\) are relevant to test
There could be many values. A loop that iterates a million times?
Binary search!
Size-variant tuning
loop:
p_1 \geq t_1
p_2 \geq t_2
v_1
v_2
v_3
Best for \(p_2 = 50, 100\)
Best for \(p_2 = 5\)
Binary search!
0, 5, 50, 100, \infty
Measure
Measure
Measure
Gradient
Assuming such a gradient exists!
Size-variant tuning
If a gradient exists, we find the optimal tuning range for a single dataset and threshold in \(O(\log p)\) runs
\(p\): number of distinct parameter values for the given threshold
Results
Compare to previous tuning tool, based on OpenTuner
- Black box
- No knowledge of program structure
- Explores enormous search space
- Optimized with memoization
Tuning-time Results
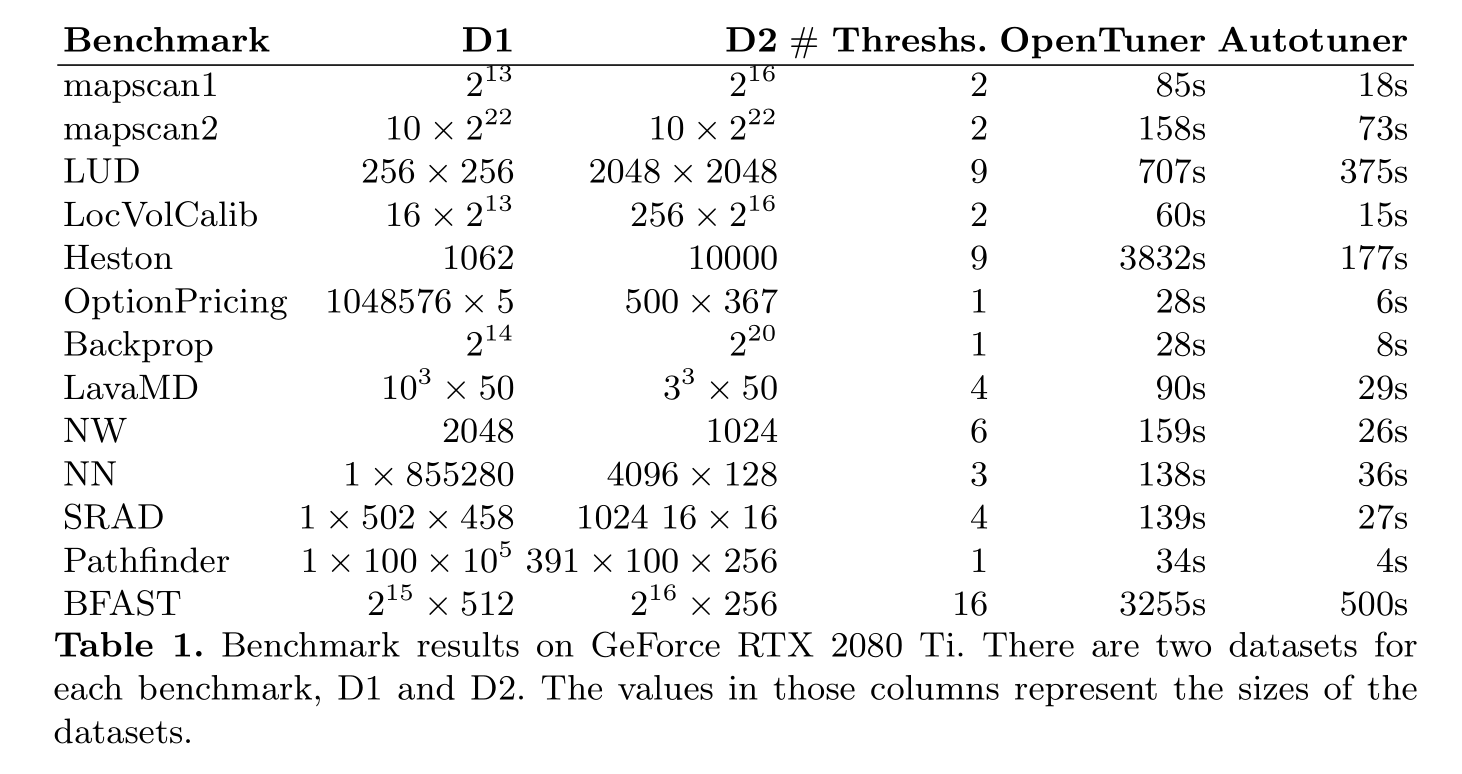
Performance of tuned program
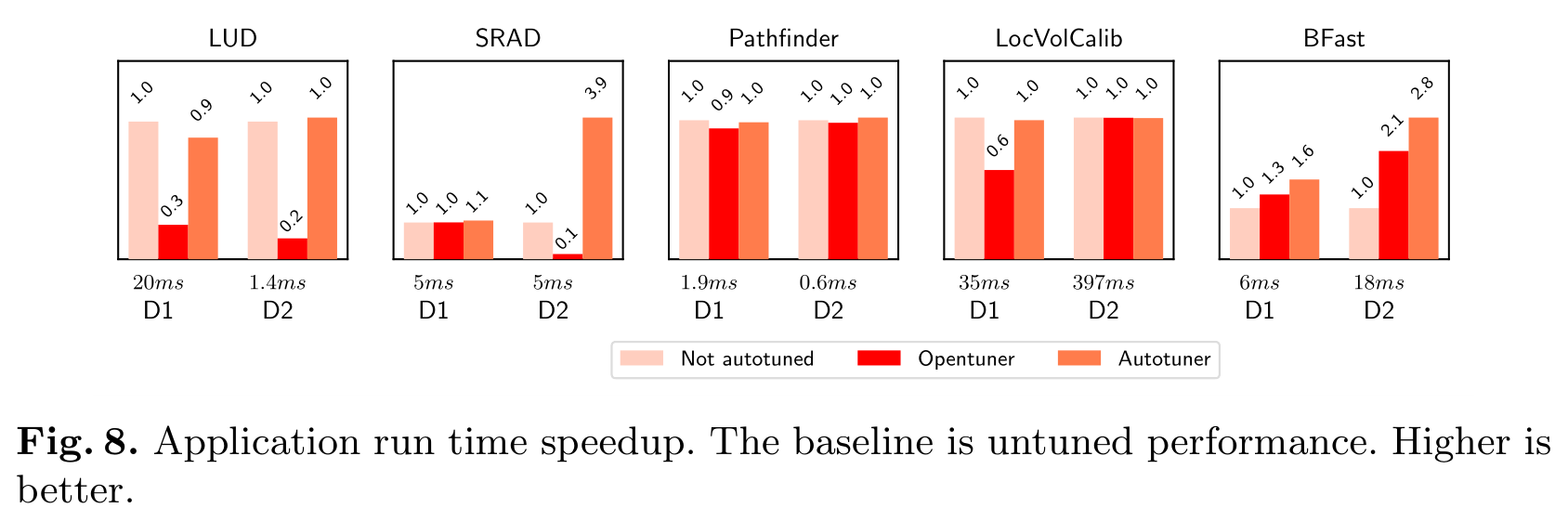
Only benchmarks which have different performance
Reliable even for programs with small number of thresholds
Other approaches
- Tune compiler flags for best average performance\(^1\)
- Multi-versioned compilation, tune for a single dataset on specific hardware
- LIFT\(^{3,4}\), SPIRAL\(^5\)
- General black-box tuning
- OpenTuner\(^6\)
- FURSIN, Grigori, et al. Milepost gcc: Machine learning enabled self-tuning compiler. International journal of parallel programming, 2011, 39.3: 296-327.
- STEUWER, Michel, et al. Generating performance portable code using rewrite rules: from high-level functional expressions to high-performance OpenCL code. ACM SIGPLAN Notices, 2015, 50.9: 205-217.
- HAGEDORN, Bastian, et al. High performance stencil code generation with Lift. In: Proceedings of the 2018 International Symposium on Code Generation and Optimization. 2018. p. 100-112.
- FRANCHETTI, Franz, et al. SPIRAL: Extreme performance portability. Proceedings of the IEEE, 2018, 106.11: 1935-1968.
- ANSEL, Jason, et al. Opentuner: An extensible framework for program autotuning. In: Proceedings of the 23rd international conference on Parallel architectures and compilation. 2014. p. 303-316.
Conclusion
Our technique combines multi-versioned compilation with a one-time autotuning process producing one executable that selects the most efficient combination of code versions for any dataset.
- Co-design between compiler and tuner
- One variable per threshold
- Maybe there is no intersection
- But in practice it works
Thank you for listening
Autotuning in Futhark
By Philip Munksgaard
Autotuning in Futhark
Presentation at TFP 2021.
