機器學習小社-1
講師 000

-
你可以叫我 000 / Lucas
-
建國中學資訊社37th學術長
-
建國中學電子計算機研習社44th學術
-
校際交流群創群者
-
不會音遊不會競程不會數學的笨
-
資訊技能樹亂點但都一樣爛
-
專案爛尾大師
-
IZCC x SCINT x Ruby Taiwan 聯課負責人
講師 章魚
-
建國中學電子計算機研習社44th學術+總務
-
是的,我是總務。在座的你各位下次記得交社費
束脩給我 -
技能樹貧乏
-
想拿機器學習做專題結果只學會使用API
-
上屆社展烙跑到資訊社的叛徒
-
科班墊神



殭屍抱柑橘
by 兩個備課備到今天2點的人
-
機器學習概論
-
機器學習的種類
-
分類問題
-
線性迴歸
-
偏微分概念
目錄
機器學習概論
蛤?
機器學習?
是什麼?
能吃嗎?
先不說機器學習
AI你肯定聽說過吧
他們兩個是一樣的嗎
AI其實是個很廣泛的名詞
機器學習只是他的一部分
大概的時間線
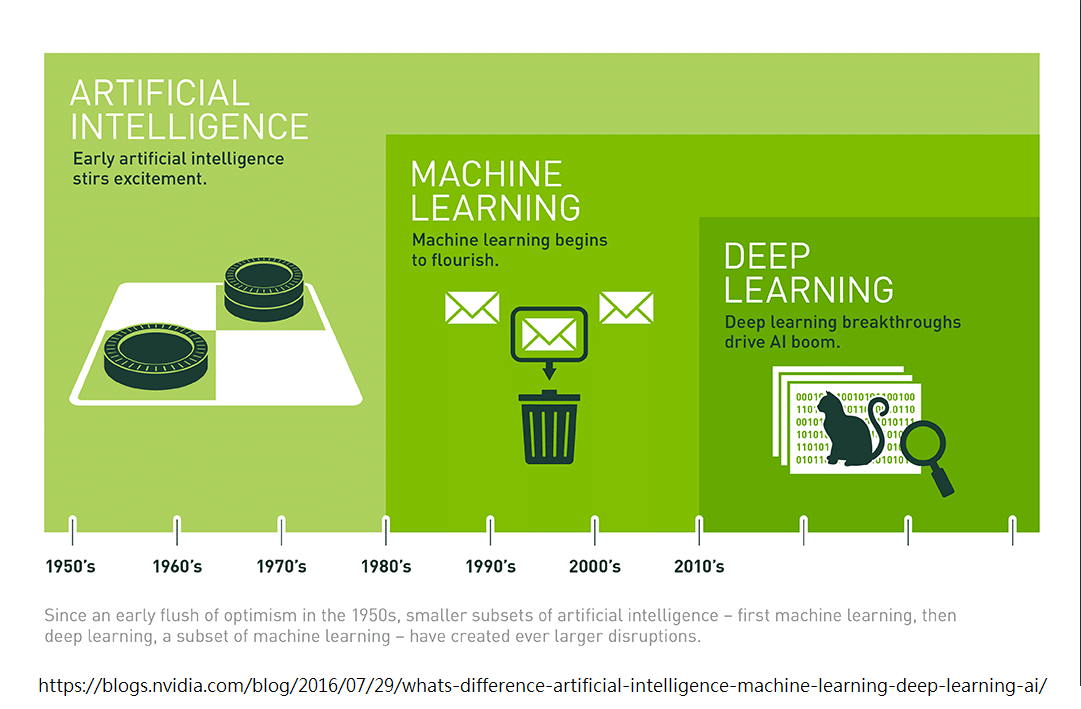
機器學習
Machine Learning
「機器學習(Machine Learning,ML)
是一種讓電腦能夠從數據中學習並做出預測或決策的技術
無需明確編寫規則
它是人工智慧(AI)的核心分支
廣泛應用於圖像識別、語音識別、推薦系統、自然語言處理等領域」
by ChatGPT
機器學習
Machine Learning
先不說別的
就我們目前認知中的人工智慧
就可以輕易的了解到機器學習的發展還是非常值得關注的
機器學習
Machine Learning






機器學習
Machine Learning


機器學習
Machine Learning






機器學習
Machine Learning



機器學習
Machine Learning






機器學習
Machine Learning


機器學習
Machine Learning






機器學習
Machine Learning




機器學習
Machine Learning






機器學習
Machine Learning



機器學習
Machine Learning






機器學習
Machine Learning



機器學習種類
人工智慧
機器學習
監督式學習
非監督式學習
強化學習
深度學習
機器學習
- 實現人工智慧最主要的途徑之一
- 透過機器學習演算法從資料中得出規律,並學習如何判斷
人工智慧
機器學習
監督式學習
非監督式學習
強化學習
深度學習
監督式學習
非監督式學習
&
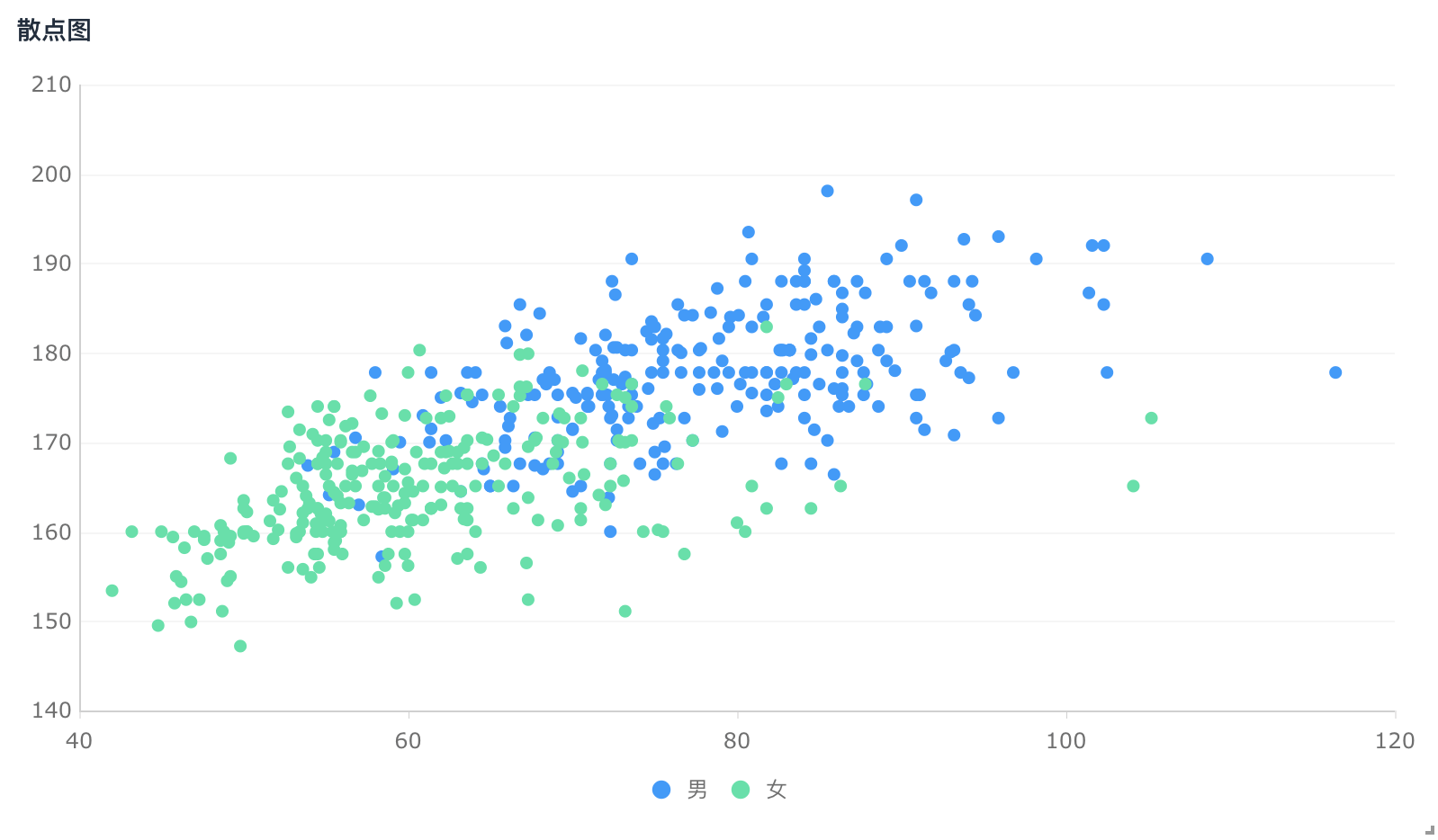
new
a boy
supervised learning
非監督式學習
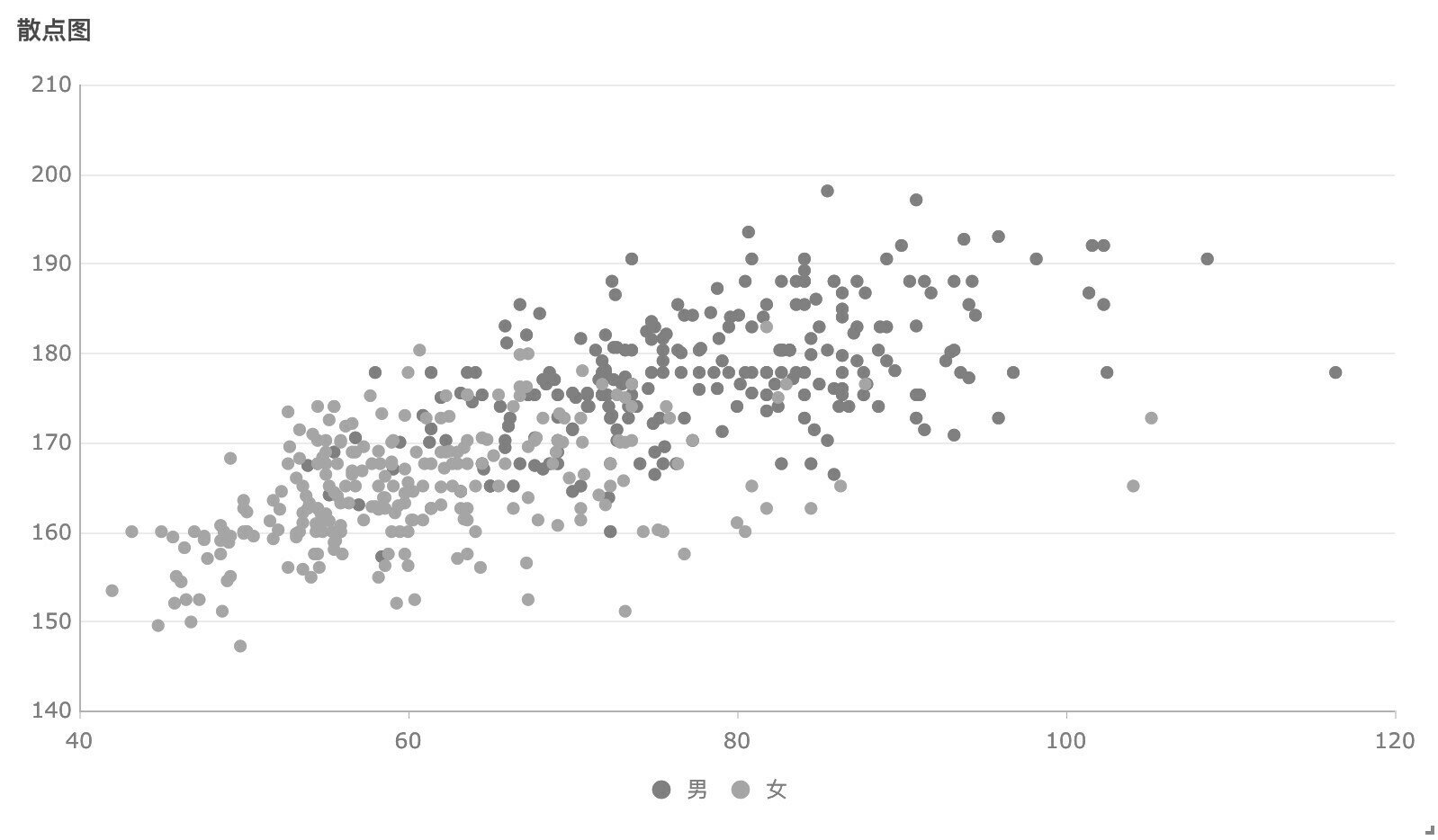
group1
group2
group3
new
group2
unsupervised learning
人工智慧
機器學習
監督式學習
非監督式學習
強化學習
深度學習
強化學習
- 在給定的環境中,學習怎麼樣才能獲得最多的獎勵
- 簡單來說,就是去學怎麼玩一款遊戲
reinforcement learning
人工智慧
機器學習
監督式學習
非監督式學習
強化學習
深度學習
深度學習
- 與監督、非監督、強化學習不太一樣,上述三個比較像機器學習的類別,而深度學習則是比較像機器學習的方法
- 使用多層的神經網路來找規律,其中又因架構不同分為標準神經網路、卷積神經網路、遞迴神經網路等
- 雖然也有其他機器學習的方法,但深度學習算是最主要的方法,接下來的課程也都會圍繞著他展開
deep learning
分類問題
分類
Classification
- 監督式學習的一種
- 目的是根據輸入數據預測類別標籤(Label)
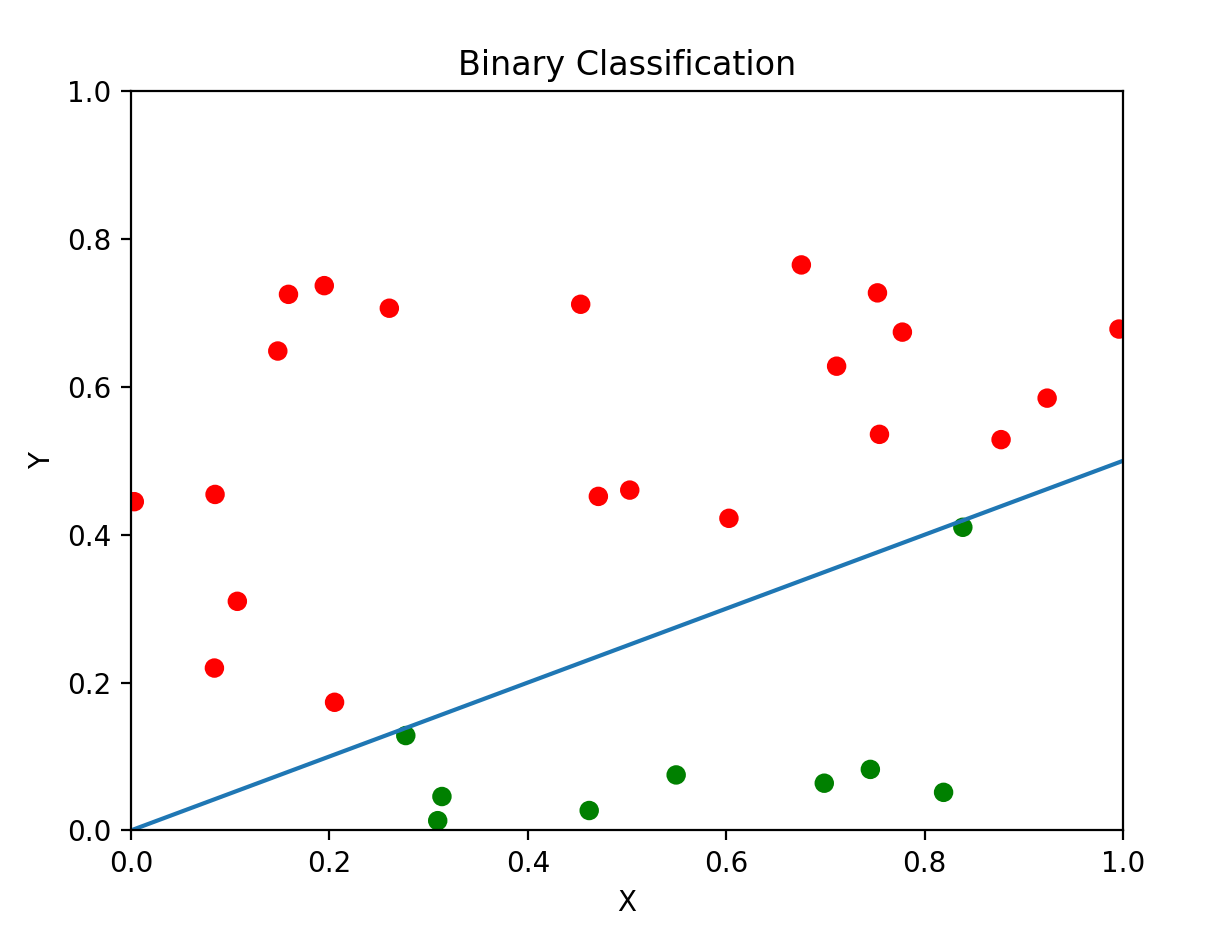
二元分類
Binary Classification
- 最簡單的分類問題,概念相當於是非題
- 有一或多個特徵(feature)輸入
- 輸出一個機率,介於0~1之間(顯然吧),代表這題答案是「是」的機率
- 機率大於0.5就當作「是」,反之,當作「否」
想法
先從最簡單的開始
假設你希望有一台機器
他能學會判斷你的成績(單一特徵)有沒有及格
所以你寫了以下程式
my_score = input("幾分?")
if int(my_score) >= 60:
print("you pass")
else:
print("you fail")這樣要機器學習有什麼用
想法
依照二元分類的想法
我們應該要輸出一個機率y
而且保證0≤y≤1
那將原始成績除以60再乘以0.5?
很接近了~但這也還不是機器學習
想法
別忘了一開始說的
機器學習是從一堆資料中找尋規律
也就是說
他知道的只有
眼前這個成績對應到的是及格還是不及格
他並不知道成績跟及格之間的關係
讓他學會這層關係就是我們的目標
比番茄醬水餃抽象?
直接來看範例
想法
首先會先人工設定一個架構
讓他在架構中學習
以剛剛的題目來說
我們可以設定為
\(y = wx\)
\(y\)->預測機率 \(x\)->成績
\(w\)->參數(parameter)
而找到合適的w就是他的目標
想法
怎麼學?
玩過猜數字吧
一開始當然是亂猜
如果猜得太大 下一次就猜小一點
反之亦然
同理 先讓w是一個隨機值
如果沒及格猜成有及格 那就把w調小一點
反之亦然
只要猜的次數夠多 必然會收斂
來實作唄
來實作唄
import random
import matplotlib.pyplot as plt
w = random.uniform(0,0.1)
w_history = []
x = [random.randint(0,100) for _ in range(100)]
y = [x[i] >= 60 for i in range(100)]
step = 0.001
for i in range(100):
yh = (w*x[i] >= 0.5)
w_history.append(w)
if yh == y[i]:
continue
elif yh == 1:
w -= step
else:
w += step
order = [i for i in range(100)]
plt.plot(order,w_history)
plt.plot([0,99],[0.5/60,0.5/60])
plt.ylim(0,0.1)
plt.show()線性迴歸
迴歸
Regression
- 監督式學習的另一種
- 目的是學習輸入數據與數值結果之間的關係
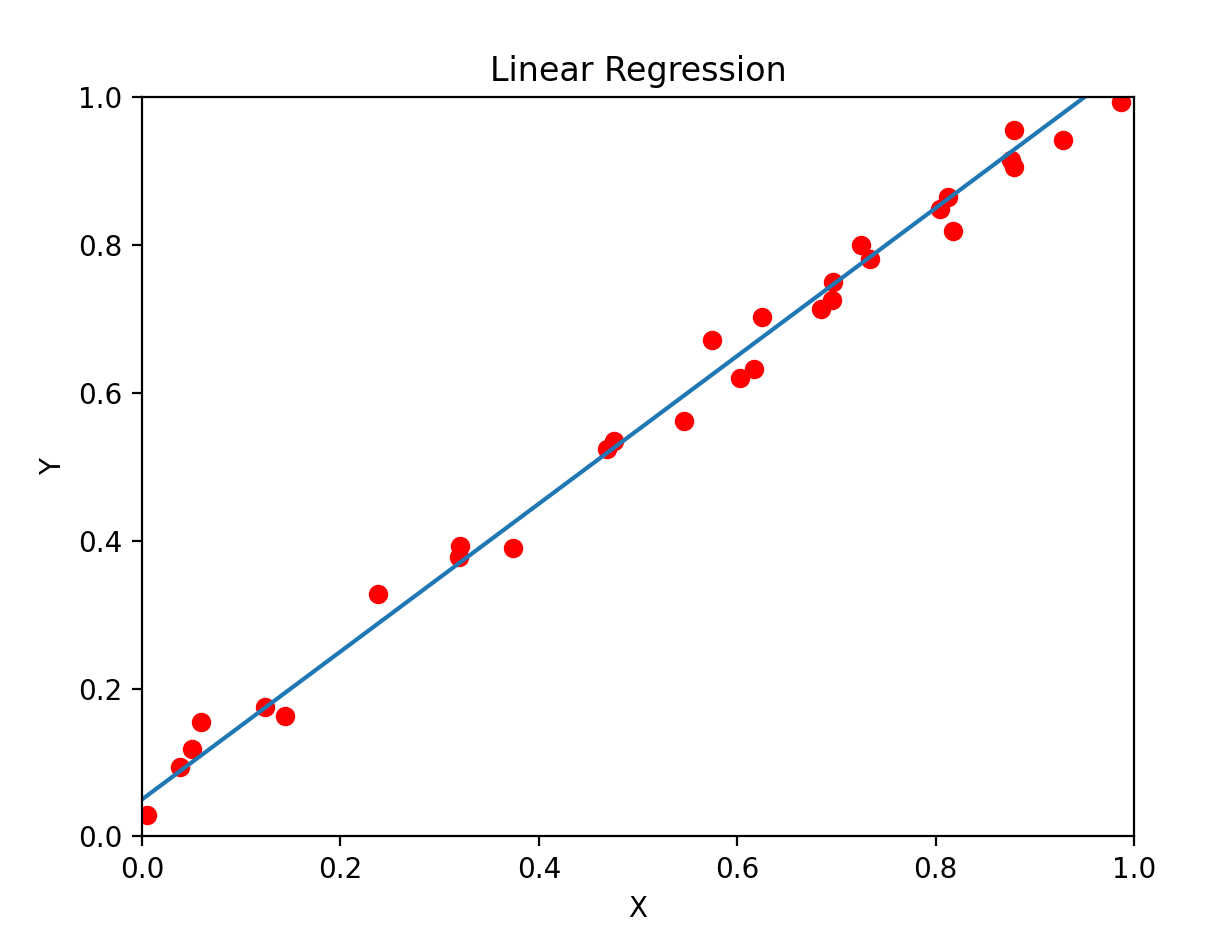
最適迴歸直線
最適迴歸直線是指 最能代表數據趨勢的直線
這條線可以用來 預測未知數據,或 分析兩個變數之間的關係
by chatGPT
假設最適迴歸直線方程式
\( y = \beta_0+\beta_1x \)
以最小平方法推得以下算式
\(\left\{\begin{matrix}\beta_1 = \frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x})^2} \\ \beta_0 = \bar{y} - \beta_1x\end{matrix}\right.\)
有n筆數據\((x_1,y_1),(x_2,y_2)...(x_n,y_n)\)
最小平方法
least squares method
用於評估直線擬合程度
有n筆數據\((x_1,y_1),(x_2,y_2)...(x_n,y_n)\)
LSE = \(\sum (y_i-\hat{y})^2\)
LSE最小的直線就是最適迴歸直線
簡單線性回歸
Simple Linear Regression
其實呢 標準答案你剛剛就知道了
但可惜我們就是要先繞一點路
我們要用機器學習的方法
同樣先給他個架構
\( y = \beta_0+\beta_1x \)
這次要學習的參數有\(\beta_0 , \beta_1\)
想法
\(y = \beta_0+\beta_1x\)
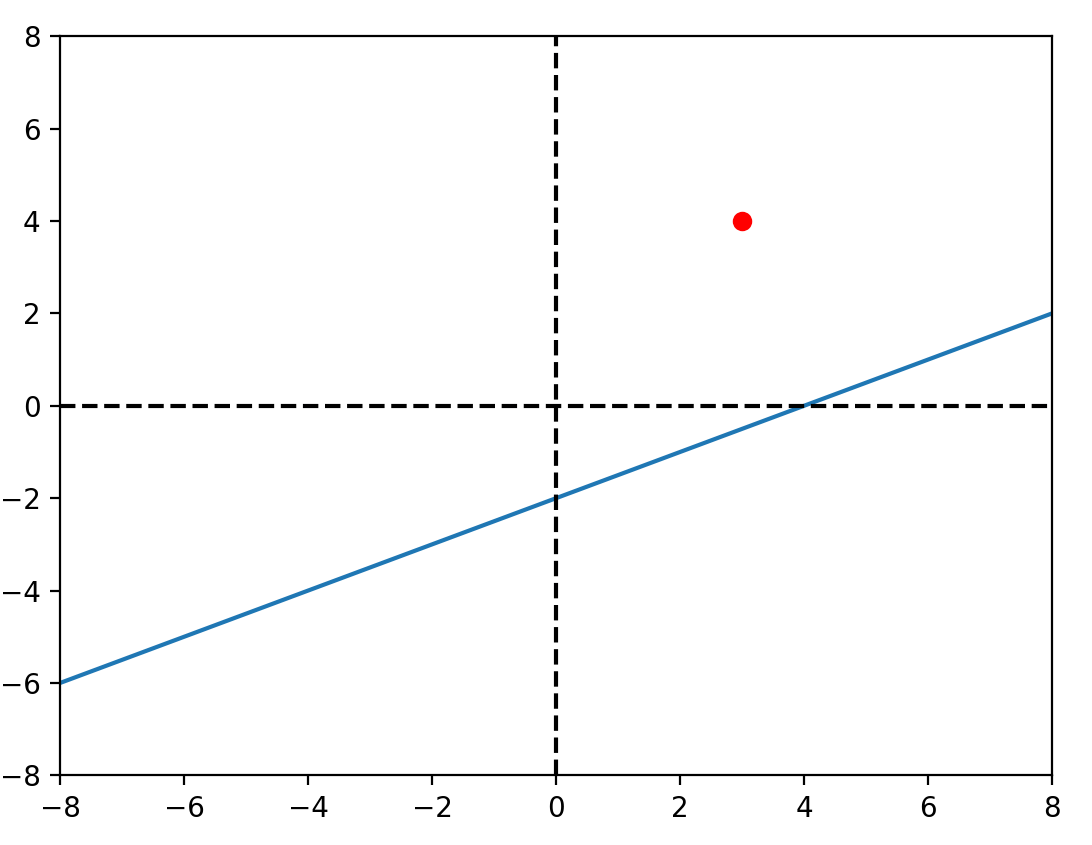
想法
\(\beta_0\)
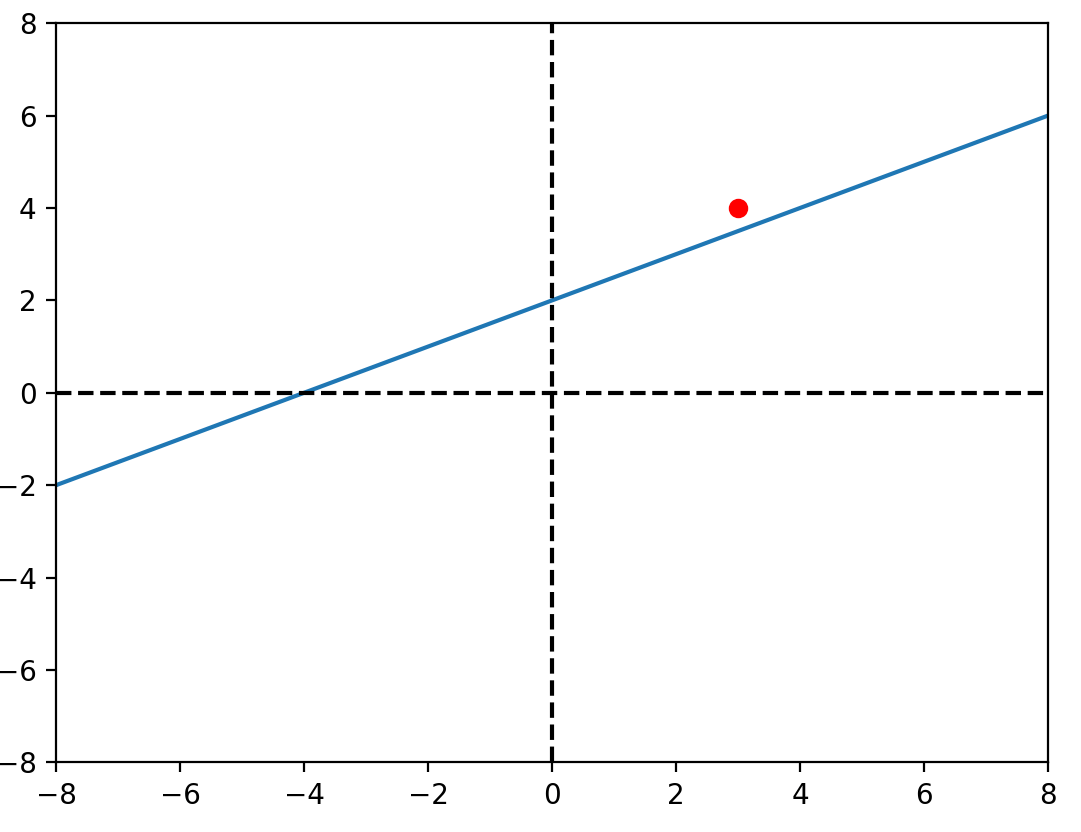
想法
\(y = \beta_0+\beta_1x\)

想法
\(\beta_1\)
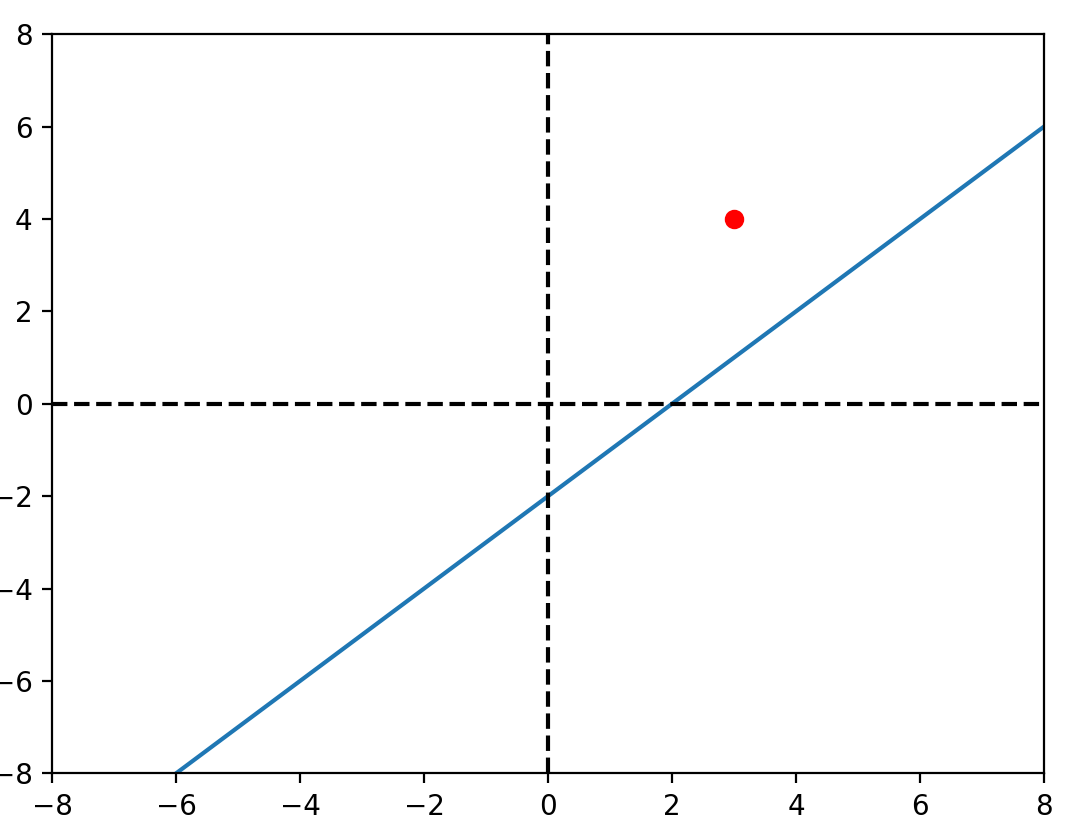
想法
\(y = \beta_0+\beta_1x\)

想法
\(y = \beta_0+\beta_1x\)
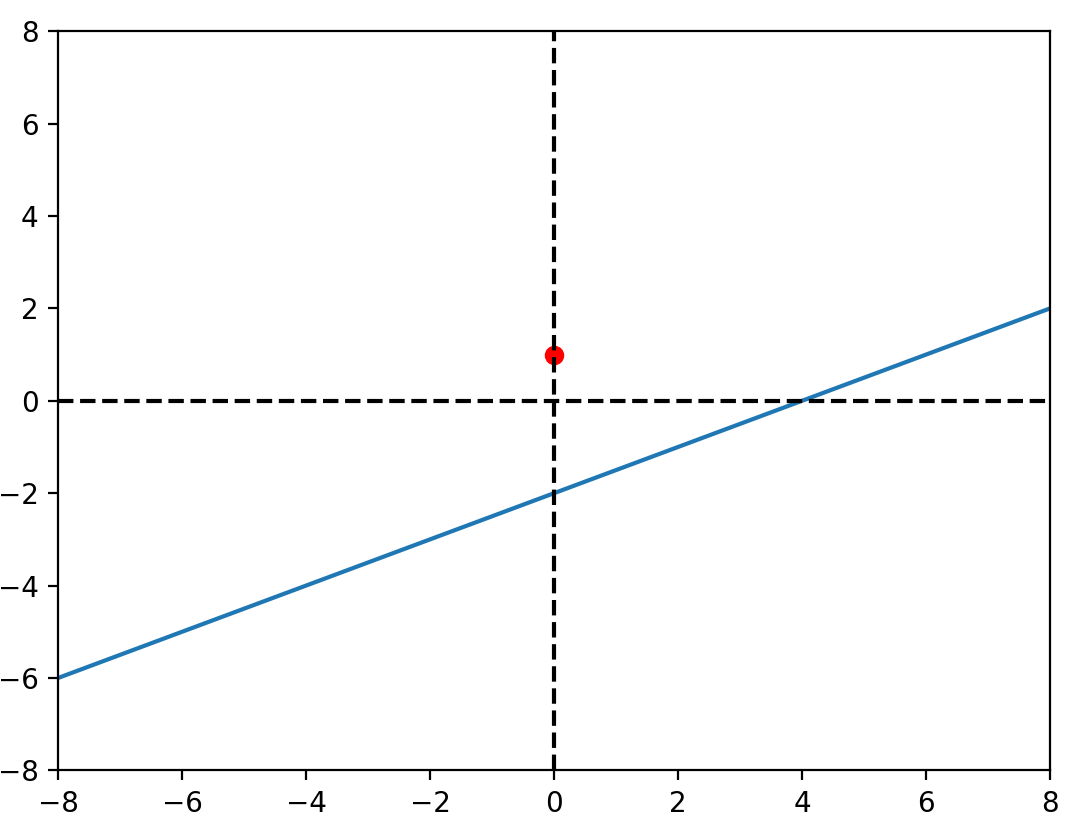
想法
\(\beta_1\)👀

想法
\(y = \beta_0+\beta_1x\)
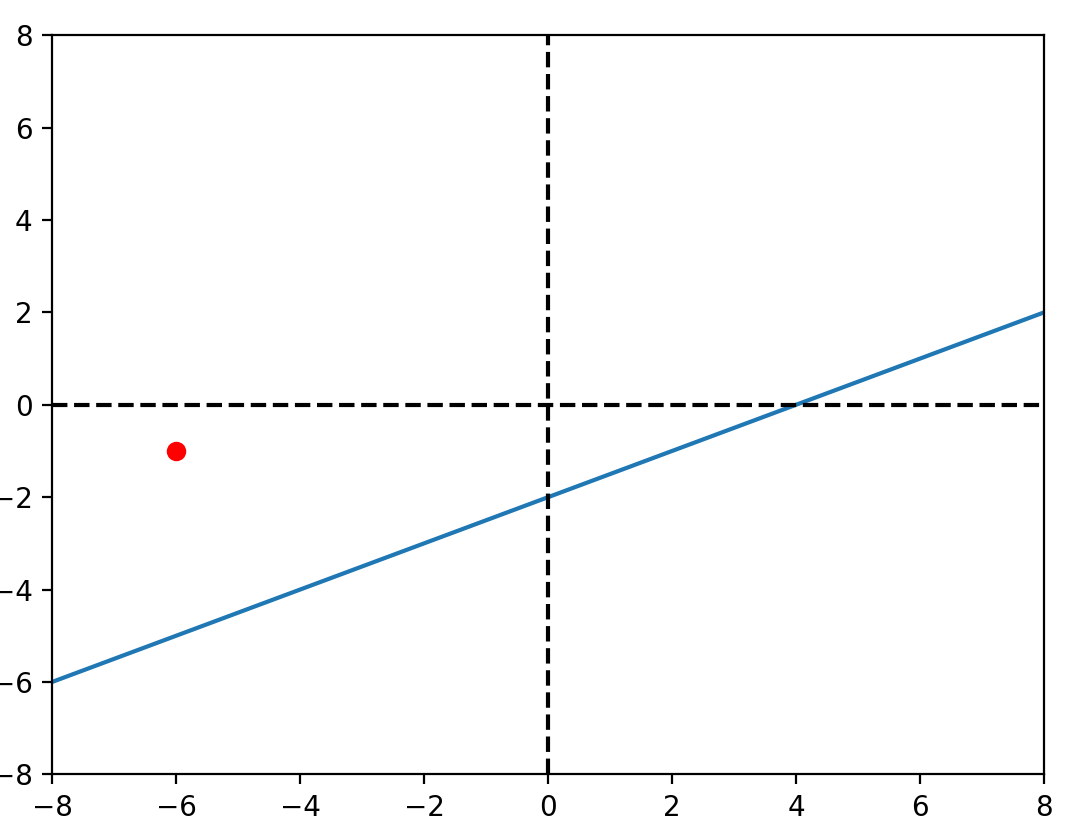
想法
\(\beta_1\)
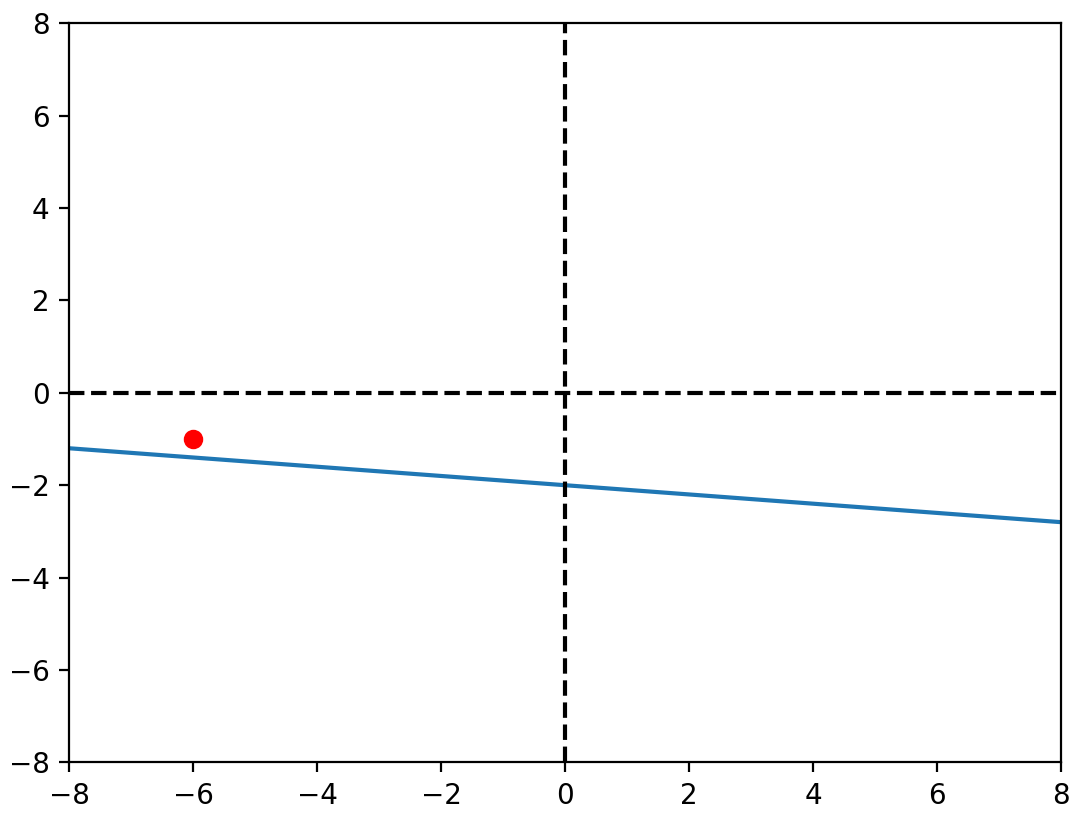
觀察
\(\beta_0\)的改變與 \(y_i-\hat{y}\) 有關
\(\beta_1\)的改變與 \((y_i-\hat{y})x_i\) 有關
實作
實作
import matplotlib.pyplot as plt
from IPython import display
import random
# y = 0.5 * x - 5
random.seed(114514)
x = [i for i in range(-50, 50, 1)]
y = [0.5 * i - 5 + random.randint(-10, 10) for i in x]
b_0 = random.uniform(-1, 1)
b_1 = random.uniform(-1, 1)
print("before train:")
print(f"b_0:{b_0}")
print(f"b_1:{b_1}\n")
alpha_0 = 0.01
alpha_1 = 0.0001
epoch = 100
def f(x):
return b_0 + b_1 * x
def delta_0(y, yh):
return -2 * (y-yh)
def delta_1(y, yh, x):
return -2 * (y-yh) * x
for _ in range(epoch):
plt.clf()
plt.plot([-50,50], [0,0], c="black", alpha=0.5)
plt.plot([0,0], [-50,50], c="black", alpha=0.5)
plt.xlim(-50, 50)
plt.ylim(-50, 50)
i = random.randint(0, 99)
yh = b_0 + b_1* x[i]
b_0 -= alpha_0 * delta_0(y[i], yh)
b_1 -= alpha_1 * delta_1(y[i], yh, x[i])
plt.plot([-50, 50], [f(-50), f(50)], c="red")
plt.scatter(x, y, c="blue")
plt.scatter(x[i], y[i], c="red")
plt.pause(0.1)
display.clear_output(wait=True)
print("after train:")
print(f"b_0:{b_0}")
print(f"b_1:{b_1}")實作1
# y = 0.5 * x - 5
random.seed(114514)
x = [i for i in range(-50, 50, 1)]
y = [0.5 * i - 5 + random.randint(-10, 10) for i in x]
b_0 = random.uniform(-1, 1)
b_1 = random.uniform(-1, 1)\(y = 0.5x -5+ \varepsilon \)
\(x = [-50, -49, ..., 49]\)
設定\(b_0,b_1\)為-1~1的隨機值
實作2
alpha_0 = 0.01
alpha_1 = 0.0001
epoch = 100這是很重要的參數們
可以試著調調看
等等會說明
實作3
def f(x):
return b_0 + b_1 * x
def delta_0(y, yh):
return -2 * (y-yh)
def delta_1(y, yh, x):
return -2 * (y-yh) * x\(yh = f(x) = b_0 + b_1x\)
delta_0跟delta_1分別代表\(b_0跟b_1\)的梯度(gradient)
至於為什麼有個-2的常數
等等會解釋
實作4
for _ in range(epoch):
plt.clf()
plt.plot([-50,50], [0,0], c="black", alpha=0.5)
plt.plot([0,0], [-50,50], c="black", alpha=0.5)
plt.xlim(-50, 50)
plt.ylim(-50, 50)
i = random.randint(0, 99)
yh = b_0 + b_1* x[i]
b_0 -= alpha_0 * delta_0(y[i], yh)
b_1 -= alpha_1 * delta_1(y[i], yh, x[i])
plt.plot([-50, 50], [f(-50), f(50)], c="red")
plt.scatter(x, y, c="blue")
plt.scatter(x[i], y[i], c="red")
plt.pause(0.1)
display.clear_output(wait=True)\(yh\)代表預測的y
透過剛剛的delta_0,delta_1計算對應的梯度
在乘上alpha(學習率,learning rate)
最後更新\(b_0,b_1\)的值
實作
import matplotlib.pyplot as plt
from IPython import display
import random
# y = 0.5 * x - 5
random.seed(114514)
x = [i for i in range(-50, 50, 1)]
y = [0.5 * i - 5 + random.randint(-10, 10) for i in x]
b_0 = random.uniform(-1, 1)
b_1 = random.uniform(-1, 1)
print("before train:")
print(f"b_0:{b_0}")
print(f"b_1:{b_1}\n")
alpha_0 = 0.01
alpha_1 = 0.0001
epoch = 100
def f(x):
return b_0 + b_1 * x
def delta_0(y, yh):
return -2 * (y-yh)
def delta_1(y, yh, x):
return -2 * (y-yh) * x
for _ in range(epoch):
plt.clf()
plt.plot([-50,50], [0,0], c="black", alpha=0.5)
plt.plot([0,0], [-50,50], c="black", alpha=0.5)
plt.xlim(-50, 50)
plt.ylim(-50, 50)
i = random.randint(0, 99)
yh = b_0 + b_1* x[i]
b_0 -= alpha_0 * delta_0(y[i], yh)
b_1 -= alpha_1 * delta_1(y[i], yh, x[i])
plt.plot([-50, 50], [f(-50), f(50)], c="red")
plt.scatter(x, y, c="blue")
plt.scatter(x[i], y[i], c="red")
plt.pause(0.1)
display.clear_output(wait=True)
print("after train:")
print(f"b_0:{b_0}")
print(f"b_1:{b_1}")偏微分概念
是的我們要講數學了。


Copy of 機器學習社課 第一堂
By oct0920
Copy of 機器學習社課 第一堂
- 46



